はじめに
Stable Diffusionなどの画像生成AIを触っているうちに、大元となった拡散モデルの理論を知りたいと思い勉強し始めました。
ここでは、個人的な理解を殴り書きして忘備録としたいと思います。
(数学科ではないので、説明がふわっとしてしまうのは申し訳ございません。雰囲気がわかることを目的としています。)
私と同じように、理論を学びたい方の手助けになれば幸いです。
拡散モデルに対する当初の理解

私の拡散モデル対する理解は、上記の図で事足ります。
「自然画像に対して、少しずつノイズを付与していき、各段階ごとにちょっとだけノイズを取り除いた画像をニューラルネットワークにより生成することを、複数回繰り返すことで、なぜか、最終的にノイズの乗っていない画像を生成できる」
別にこの理解は間違っているわけではないですが、なんでその手法にしたのか、なぜその手法でノイズが綺麗に取り除かれるのかという質問には答えられません。
この理解をスタートにして、より詳細な理解をしていきたいと思います。
理解のために勉強したおすすめの本
本記事は、下記の本からの理解を多分に含んでおります。
難しい数式なども非常に分かりやすく解説しており、とてもおすすめです。
拡散モデルを理解したい方は、全員購入するべきだと思います
拡散モデル データ生成技術の数理
下記の本は数式とまではいかなくても、ある程度コードを参照しながら大まかに理論を知りたい方に非常におすすめです。
上の本よりもとっつきやすく拡散モデルの理論に触れることができます。
ゼロから作るDeep Learning ❺ ―生成モデル編
生成モデルとは
大量の自然画像が含まれているデータセットDを用意します。
自然画像一枚一枚をx_k(kは自然数)とすると、
と表すことができます。
これらの画像x_kがすべて、神が定めた自然画像の確率分布p(x)からサンプリングされているとします。
このp(x)の分布の形は人間には把握できません。
わかっているのは、この確率分布に則ってサンプリングされた画像は自然画像っぽい画像になり、実際にデータセットDの画像は、すべて、この確率分布p(x)からサンプリングされたと仮定できるということです。
では、
この神が定めたp(x)を何らかの方法で表現することができれば、世の中のどんな自然画像でも生成できるのではないか??
と考えるのは不自然なことではないと思います。
(p(x)さえわかれば、あとはそれに則ってサンプリング(1画素1画素の値を決定)していけば、おのずを自然画像が作成されます)
急に現れたように見えるp(x)ですが、世の中のすべての自然画像の確率分布というものを考えることで、どうしたら画像を生成できるのかの見通しが立ったと思います。
ではここまでの理解から、画像生成AIがどのように画像を生成しているのかを考えます。
まず、実際には把握できない神のみぞ知る自然画像確率分布p(x)が存在すると信じます。
(下の図はただのイメージです。多次元の分布を横軸の1次元で表現しています。)
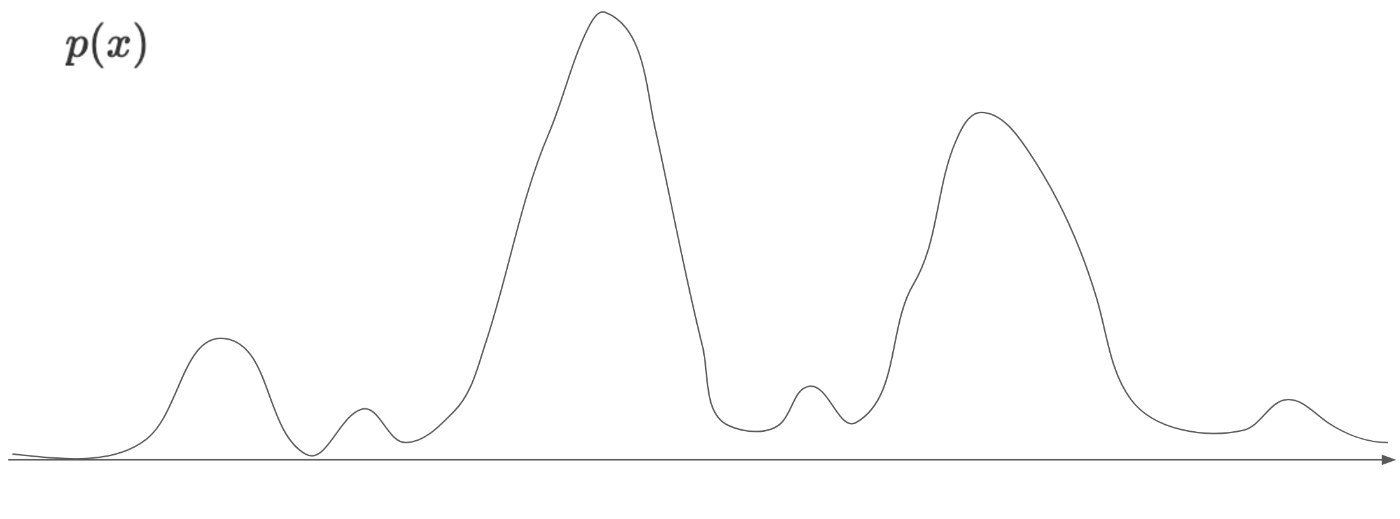
横軸は、特徴量の値、縦軸はその確率密度です。
確率密度なので、上記のグラフをすべて積分すると1になります。
特徴量の値というのは、
サイコロの例で言うと、出目の種類(1-6)
画像の例で言うと、ある1画素の値(0-255)などです。
そして、
我々の手元には、世の中のいろんな媒体から集めた大量の画像を含むデータセットDが存在します。
では、そのデータセットDが、横軸上のどの位置に存在するのかサンプリングしてみます。
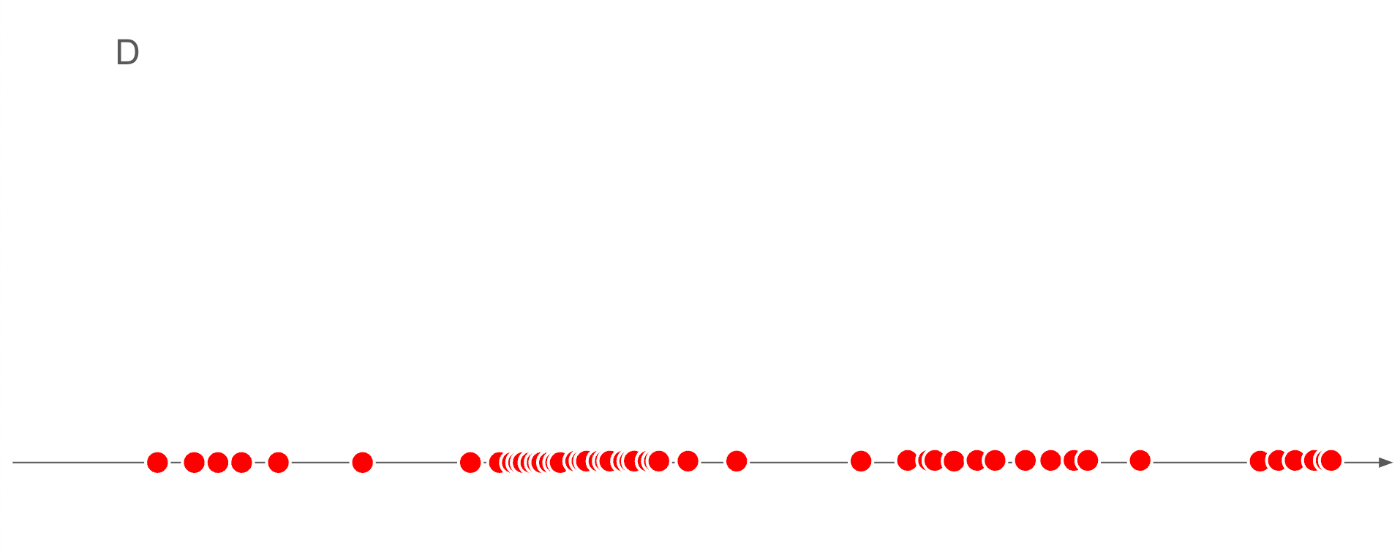
上記は、データセットD内のすべての画像を、特徴量の値に応じてプロットしています。
これだけだと、何が何だかわかりませんね。
では上記の図に、確率分布p(x)を重ねてみます。
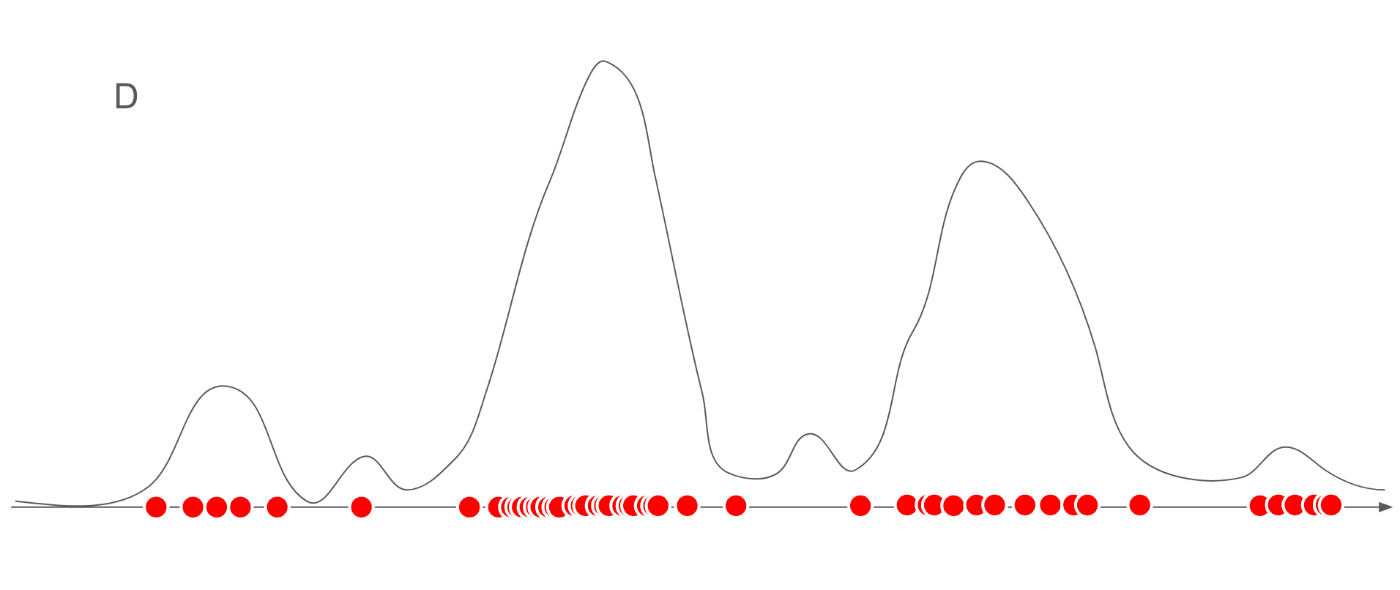
データセットDは確率分布p(x)からサンプリングされたデータなので、山が高い(確率が高い)箇所では、多くサンプリングされており、山が低い(確率が低い)箇所ではあまりサンプリングされていないことがわかります。
また、サンプリングは確率的な操作であるため、若干偏っていることもわかると思います。
例えば、右端と左端の山に注目すると、左端の山の方が高いですが、データセットには右端の特徴をもつ画像の枚数の方が多いことが見て取れます。
これは、サイコロの出目が完全な1/6ではなく、少し偏るように、データセットの中の画像も、偏りがあることを示しています。
では、ここまでで画像の特徴を抜き出すことができたので、あとは、この赤丸のデータ点に合わせて、p(x)を推定します。
この推定分布のことを、真の分布p(x)とは区別して、\textcolor{red}{q(x)}として考えます。
例えば、下記の赤線のように推定できたとします。
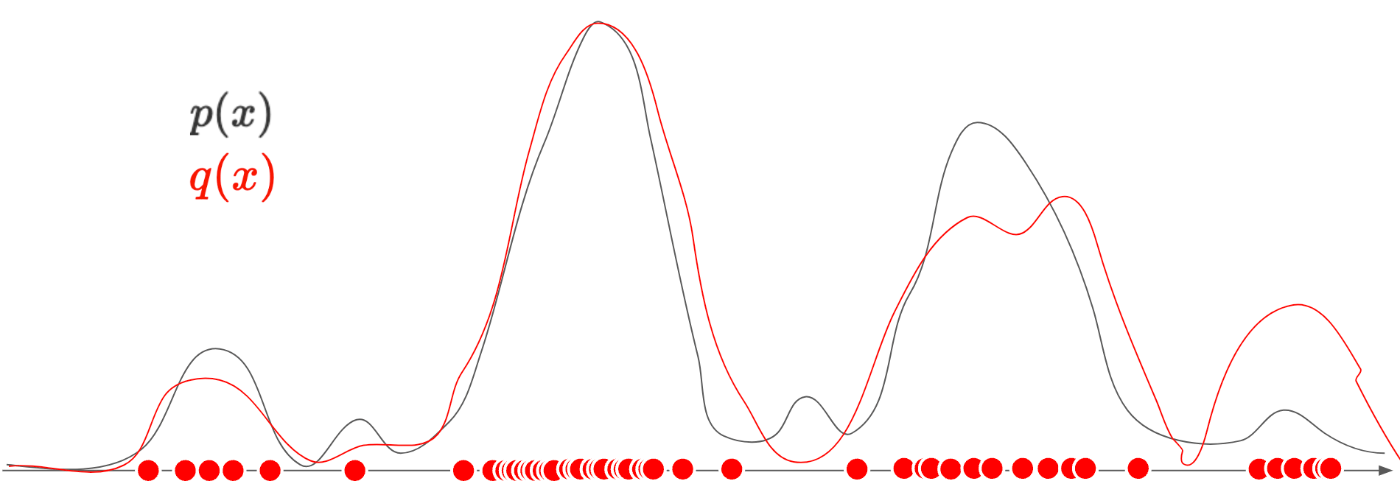
赤線が、推定した分布\textcolor{red}{q(x)}であり、黒線が真の分布p(x)です。
元のデータ点に基づいて、データ点の個数が多いところを高い確率に、少ないところを低い確率として考えて分布を作ると、(若干のずれがありますが)真の分布に近い分布を推定することができます。
(どうやって作るのかは後述します)
何よりも、このq(x)は神が与えた分布ではなく、人間が推定した分布のため、人間が使うことができます。
あとは、この推定分布q(x)の確率分布に則って画像をサンプリングすることで、新しい画像を生成することができます。
これが生成AI全般の仕組み(というか前提)になります。
推定分布を作る方法
では、どうやって、データ点から推定分布を作るのかを解説します。
これこそが、生成AIの目的関数ともなる重要な内容です。
とは言ってもそんなに難しい内容ではありません。
データ点から推定分布を作る方法は、対数尤度を最大化することです。
すなわち、生成AIの目的関数は対数尤度の最大化になります。
そもそも尤度って何?
尤度というのは、確率密度関数に対して、観測値を入力した値です。
ここで、確率分布にパラメータθを導入します。
θは確率分布を作るパラメータのまとまりです。一つの値ではなく、確率分布を生成するために必要なすべての値をまとめたものがθです。
今後は、分布を表す際に、パラメータθも導入して、p_θ(x)と表すことにします。
これにより、この分布p_θ(x)は明示的にθによって(のみ)形が制御されていることとします。
では、本題の尤度に戻ります。
例えば、推定された確率分布q_θ(x)において、あるサンプリングされた画像X_kの尤度は、q_θ(x_k)となります。
尤度を利用した分布の推定
この時、q_θ(x_k)の値が大きいのと、小さいのと、どちらがより正しくq_θ(x)を推定できていると思いますか?
では具体例を見てみましょう。
まず、ある真の分布から、3つほどデータをサンプリングしたとします。
そのサンプリング点は下記であるとします。

このサンプリング点に対して、二つの推定分布q_{θ0}(x), q_{θ1}(x)を用意します。
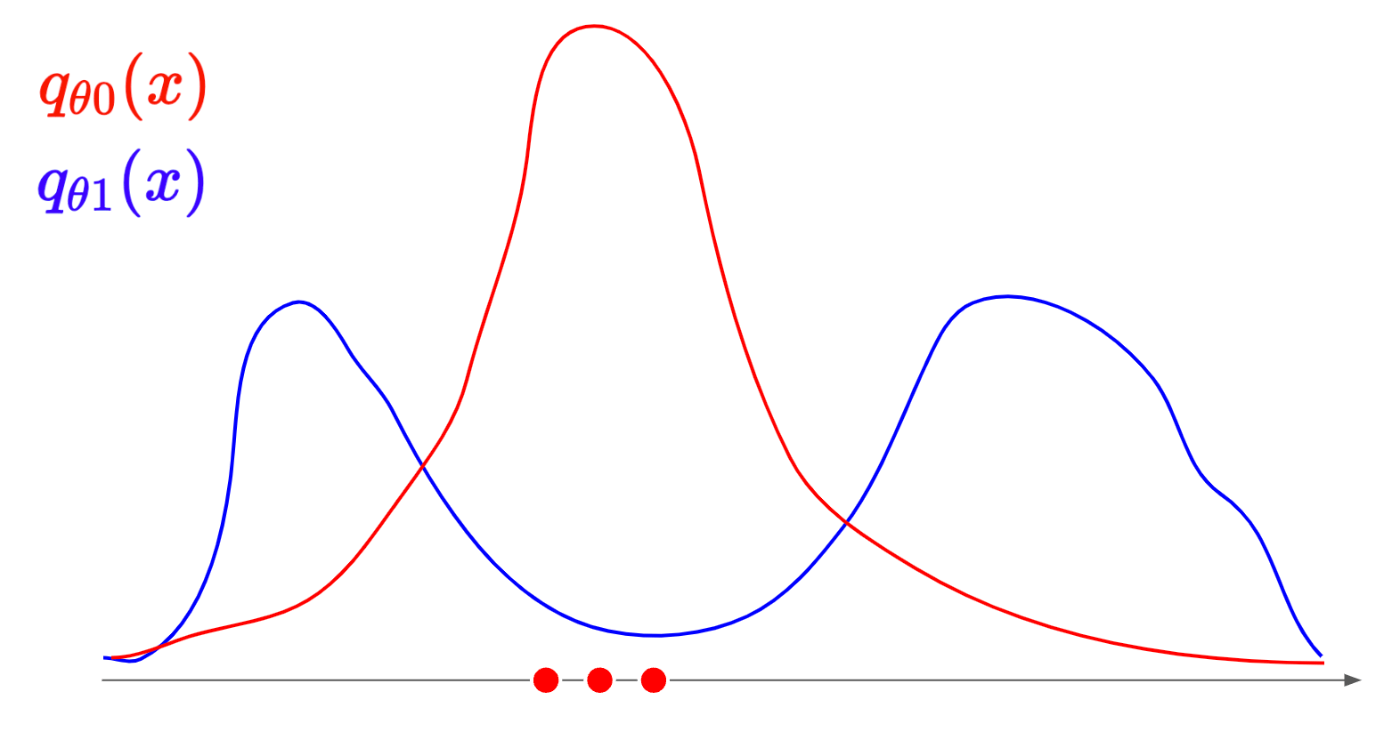
ぱっと見で、どちらの分布からサンプリングされたっぽいか、わかると思います。
もちろんq_{θ0}(x)(赤線の分布)です。
もし、q_{θ1}(x)(青線の分布)からサンプリングされていたら、青線の山の下にサンプリングされたデータ点がプロットされている可能性が高いです。
では、この感覚をどうやって、数学的に処理をするか、それが尤度L(θ)です。
ここで尤度は下記の式によって表されます。
L(\theta; x_1, x_2, \dots, x_n) = \prod_{i=1}^{n} q_{\theta 0}(x_i)
これを視覚的に理解すると下記の赤線同士、青線同士で長さの積が尤度になります。
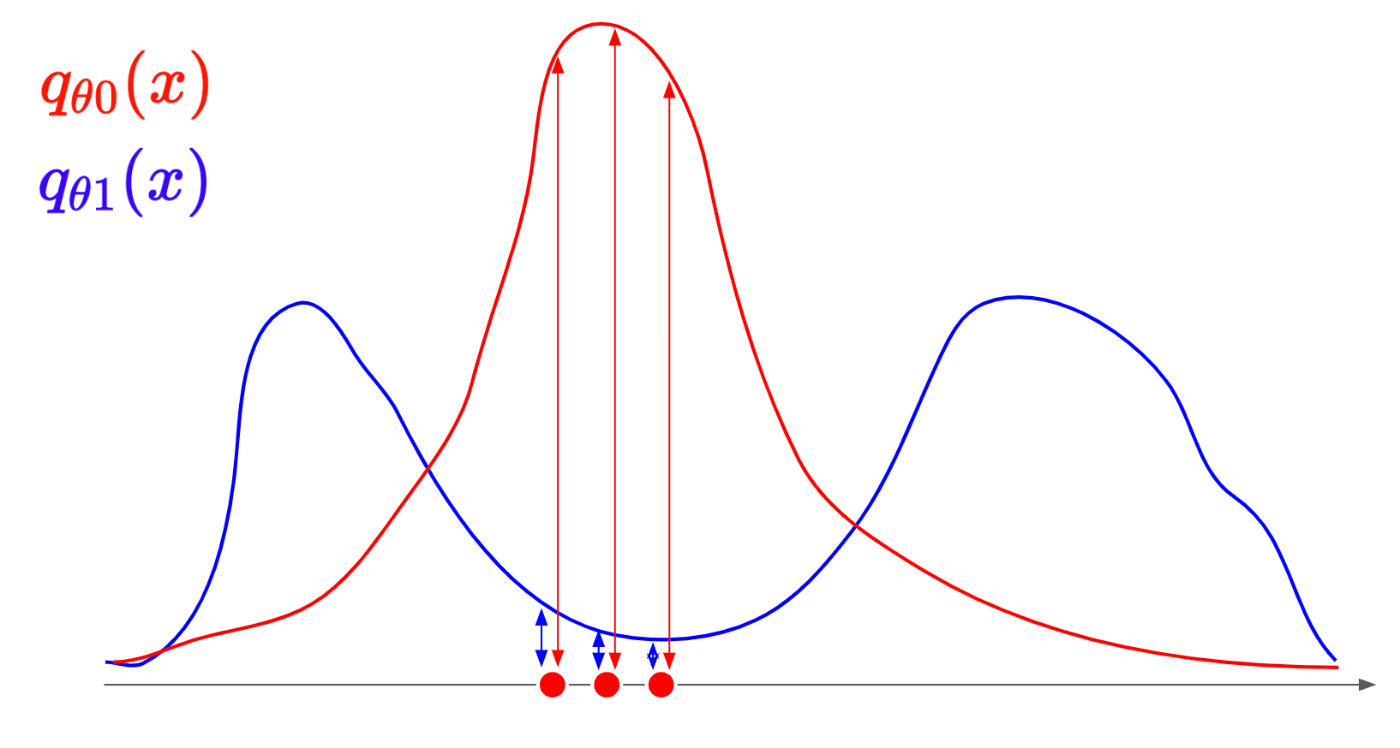
つまり、線が長い方が尤度が高くなります。
そして、この尤度を最大化する(つまり各データ点におけるq_{\theta}(x_i)の値の積)を最大化するように、
パラメータ\thetaを最適化することで、
推定しているq_{\theta}(x)の精度を向上させることができます。
対数尤度の最大化
ここまでで、核は説明しましたが、実際に生成AIが最大化するのは、尤度ではなく対数尤度です。
対数尤度は下記の式で定義されます。
\ell(\theta; x_1, x_2, \dots, x_n) = \log L(\theta; x_1, x_2, \dots, x_n) = \sum_{i=1}^{n} \log f(x_i|\theta)
つまり、尤度L(\theta)に対して、対数を取ったものです。
では、なぜ対数を取るのか?
それは、数値的に扱いやすくするためです。
まず尤度の定義式を再掲します。
L(\theta; x_1, x_2, \dots, x_n) = \prod_{i=1}^{n} q_{\theta 0}(x_i)
みてわかるように、数値の積で表されています。
しかし対数を取ることで、積の形から和の形に変わります。
積の形よりも和の形のほうが「微分」がしやすいため、最適化の計算がしやすくなります。
また対数は単調増加関数であるため、尤度の最大化と対数尤度の最大化とで得られるパラメータ\thetaは変わりません。
以上の理由から、尤度に対しては対数をとります。
分布を作る方法
確率分布を表現したい
ここまでで、生成AIが画像を生成するためには、
- データセットDから、最尤推定を用いてパラメータ\thetaを最適化して、確率分布q_\theta(x)を推定する。
- 推定した確率分布q_\theta(x)から、データ点をサンプリングする。
が必要とわかりました。
では、確率分布q_\theta(x)はどのように表現すれば良いのでしょうか。
「生成モデルとは」の章で触れたように、画像の特徴量はh \times w \times cだけの次元が必要です。
高次元の特徴を分布として表現する手法はいくつかあります。
例えば混合ガウスモデル(GMM)です。
混合ガウスモデルとは、多次元のガウス分布(正規分布)を複数用意して、それらの重ね合わせでデータをモデル化する確率モデルです。
定義式は下記のようになります。
p_\theta(x) = \sum_{k=1}^{K} \pi_k \mathcal{N}(x | \mu_k, \Sigma_k)
ここで、\pi_k は各成分の重み(混合係数)であり、\mathcal{N}(x | \mu_k, \Sigma_k)は平均 \mu_k と共分散 \Sigma_k を持つ第 k 成分のガウス分布です。
この式からみてわかるように、複数の正規分布を重み付総和しています。
こうすることで、単一の正規分布では一つの山しか表現できないですが、混合ガウスモデルでは複数の山(最大でK個)の山を表現できるようになります
しかしながら、正規分布のような単純な分布をいくつ重ね合わせても、画像生成AIとして利用するのは難しいです。
その理由は複数ありますが、
特に重要なのは画像データの「非線形性」です。
画像データには複雑な構造や非線形な特徴が含まれています。
物体の形状や輪郭は非常に複雑です。また、物体に注目した際に、視点が変わったり照明が変わることで形状や色の見え方なども変化します。その上局所的なテクスチャを表現する必要があったり、色空間RGBは独立ではなく非常に複雑に絡まり合い、画像は表現されています。
したがって、確率分布q_\theta(x)をモデル化する際には、この複雑な画像特徴を非線形でモデル化できる、非常に表現力の高いモデルが必要になります。
そこで出てくるのが、深層学習モデルであり、拡散モデルになります。
拡散モデルを導入する
導入する拡散モデルのパラメータを\thetaとします。
拡散モデルは非線形な深層学習モデルのため、非常に高い表現力を持っています。
(ここでは、データセットDから得られる確率密度q(x)を表現できるくらいの表現力があるとします)
そして、モデル自体が確率分布のモデル化とサンプリングまで行います。
つまり、このモデルは確率分布を出力するのではなく、サンプリング結果を出力します。
(確率分布を出力する例)
(サンプリング結果を出力する例)

拡散モデルでは、サンプリング結果を出力するため、モデルの出力として得られるのは、画像自体になります。
従って、確率分布自体は明示的に出力されません。
しかしながら、「推定分布を作る方法」の章で解説した通り、生成AIの目的関数は、対数尤度の最大化による確率分布のパラメータの最適化です。
「では、確率分布を出力せずに、確率分布を最適化することができるのか??」
「そもそも、生成AIは本当に確率分布を学習しているのか?」
という疑問が出ると思います。
生成AIは本当に確率分布を学習しているのか?
まずは、2つ目の疑問から回答することにします。
ここでは、Reparameterization Trickのような考えを使っていると私は理解しています。
では、本題に戻ります。
なぜ、確率分布を出力せずに、確率分布を最適化することができるのか??
それは、ここまでの内容を考慮すると、
深層学習モデル(拡散モデル)自体が、分布を変換させる関数G(x)を学習しているからです。
つまり、深層学習モデルをQ_\theta(x)とすると、拡散モデルの入力を標準正規分布\mathcal{N(\mu,\theta)}からサンプリングしたx_nを利用すると、下記が成立します
Q_\theta(x_n) \sim q_\theta(x)
ただし、
x_n \sim \mathcal{N(\mu,\theta)}
であり、
q_\theta(x)はデータセット
Dから最尤推定された推測分布です。
拡散モデルでは、Q_\theta(x)の計算グラフを最適化し、分布変換の式を最適化しています。
従って、拡散モデルは確率分布を学習している(正確には「正規分布のような単純な分布から、自然画像の確率分布という複雑な分布への変換を学習している」)ということができると思います。
ただ、これでもまだ、
「なぜ、確率分布を出力せずに、確率分布を最適化することができるのか??」
の疑問に対して回答していません。
この問題は、これまで非常に多くの研究者を困らせた問題になります。
対数尤度の最大化というのは下記で表せます。
\ell(\theta; x_1, x_2, \dots, x_n) = \sum_{i=1}^{n} \log q_\theta(x_i)
しかしながら、\log q_\theta(x_i)を計算することは非常に困難です。
従って、これまでの生成AIのうち、サンプリングされた結果を出力するモデル(画像自体を出力するモデル)であるVAEやGANでは、この対数尤度を直接最大化するのを諦めています。
しかしながら、拡散モデルでは、この「対数尤度の最大化」という問題に真っ向から挑んでいます。
そして、対数尤度を直接最大化することに成功しているため、非常に高精細な画像が出力できるようになったと思っています。
確率分布を出力せずに、確率分布を最適化することができるのか??
この章からが、拡散モデルを理解する本題に入ります。
この章は一番数式が出てきます。また微分方程式などの難しい概念が入ってくるので、まずは、これまでの説明をベースにして、拡散モデルがやっていることを感覚的に理解することを目的にします。
拡散モデルを感覚的に理解をする
拡散モデルによるデータ点の更新方法
まずは、下記のように、
神のみぞ知る自然画像の確率分布p(x)を考えます。
加えて、完全ランダムな分布からサンプリングされた青色のデータ点x_Tを考えます。
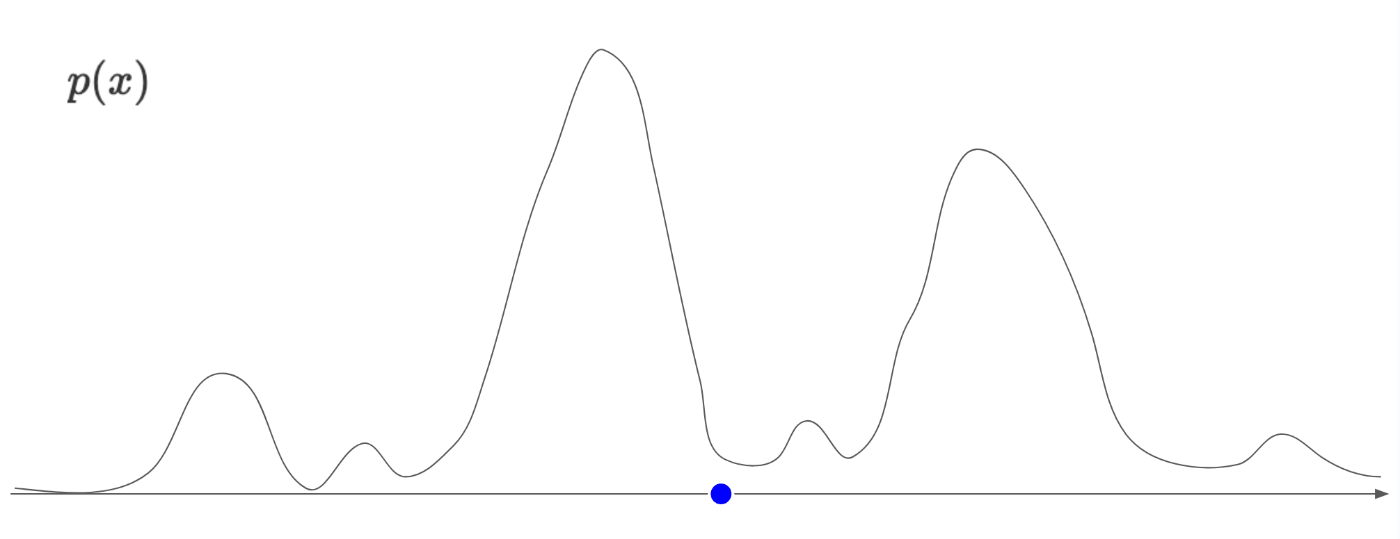
この場合、青い点はp(x)の山の低いところにいるため、おそらく自然画像ではなく、ランダムノイズなどの意味のない画像であることが推測できます。
もし、この青いデータ点を、p(x)の山の高いところ移動することができれば、データ点を自然画像に近づけることができます。
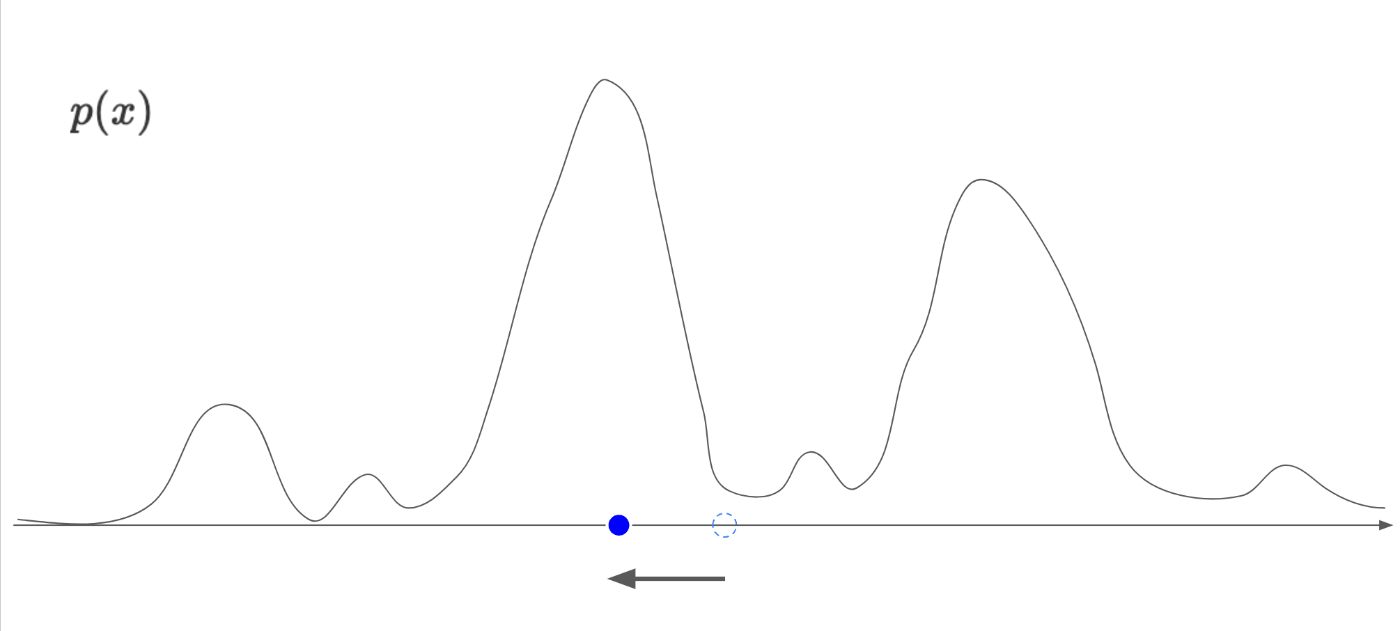
では、この山の高いところにどうやって移動するのか。ここでデータ点x_Tでのp(x)の勾配\nabla_{x_T} p(x_T)を考えます。
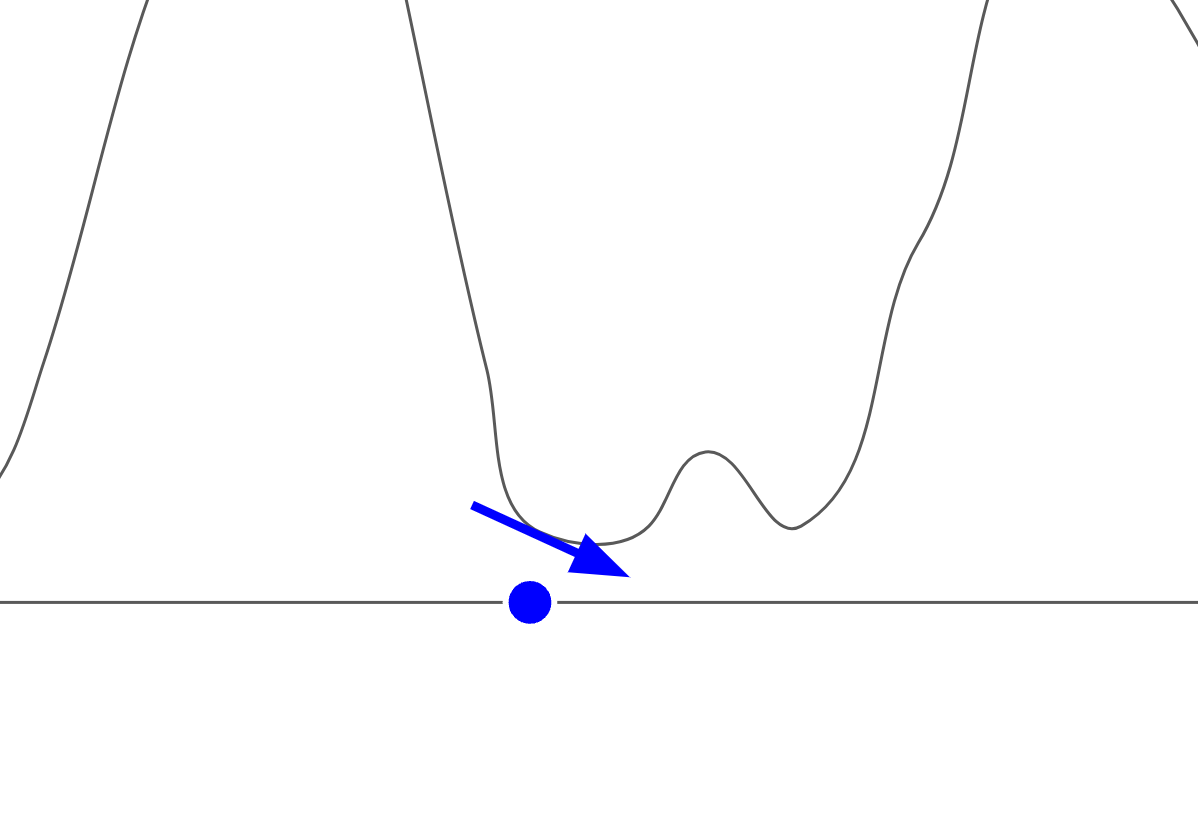
勾配を考えるというのは、下記の通り、微分を考えるということに他なりません
\nabla_{x_T} \log p(x) = \frac{\partial}{\partial x_T} \log p(x)
(ここで、以前の章で解説した通り、尤度から対数尤度を導入します)
上記の図で考えると、\nabla_{x_T} p(x_T)は負の値になります。
また、図を考えると、青いデータ点は左の方向、すなわち負の方向に動かしたいです。
従って、下記のようにデータ点を動かすことができれば良いことがわかります。
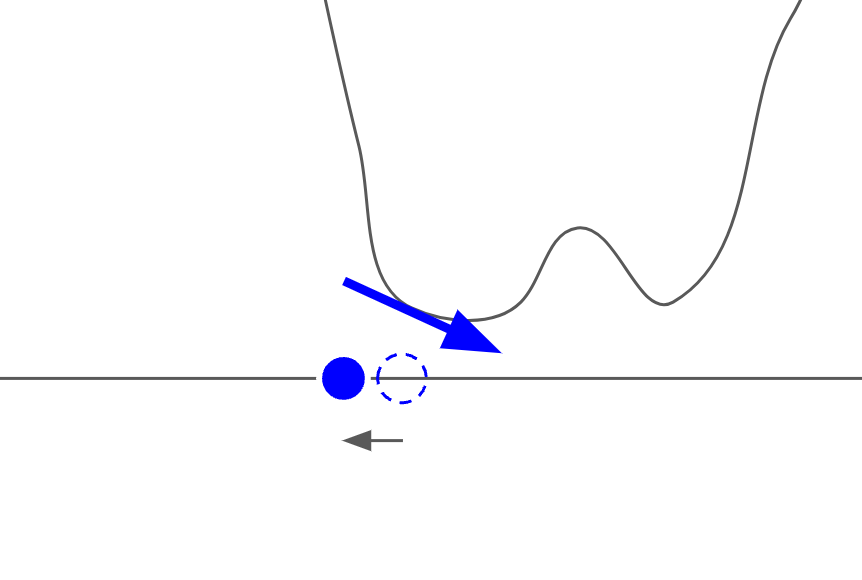
式として表すと、下記の微分方程式が得られます。
dx = \alpha \nabla_{x} \log p(x)dt
すなわち、無限回の試行回数を伴って、微小幅dtの幅で、データ点xは対数尤度\log p(x)を最大化する方向に更新されていることがわかります。
(対数尤度を最大化する方向に更新しているため、自然画像にどんどん近づいていきます)
(\alphaは変化量の係数です。)
しかしながら、無限回の試行回数を現実的に実施できないため、離散化した場合の式を下記に示します。
x_{T-1} = x_T + \alpha \nabla_{x_T} \log p(x)
ここで、
Tの値は大きければ大きいほど、連続的な微分方程式の解との誤差が小さくなります。
Tの値はしばしば1000が利用されます。
従って、最終的にT回、データ点xに対して更新を行うことで、ノイズ画像x_Tから自然画像x_0に変換されます。
変換する際に、対数尤度\log p(x)を最大化する方向に更新しているため、T回の拡散モデルによる更新を伴って、生成されたデータ点x_0は、対数尤度を最大化する問題を解いた上で得られるデータ点であることがわかります。
では、どうやって拡散モデルにおいて、勾配\nabla_{x_t} \log p(x_t)を取得すれば良いでしょうか。
実際に拡散モデルで実施している方法としては、ある1Stepの拡散モデルの入出力として、
入力が、tステップ目の更新後データ点「x_{t}」
出力が、勾配「- \alpha \nabla_{x_{t}} \log p(x_{t})」となるようにネットワークを学習しています。
こうすることで、ネットワークの出力が、そのまま勾配- \alpha \nabla_{x_t} \log p(x_t)となるため、あとはネットワークの入力x_tに対して、- \alpha \nabla_{x_t} \log p(x_t)を減算してやることで、次のステップのデータ点x_{t-1}が得られます。
拡散モデルによる勾配の学習方法
では、ここで疑問となるのが、
「どうやって、ネットワークが勾配「- \alpha \nabla_{x_{t}} \log p(x_{t})」を出力できるように学習させるのか?」という疑問だと思います。
その疑問に回答するために、まず勾配「- \alpha \nabla_{x_{t}} \log p(x_{t})」がどのようなものかを考えます。
勾配「- \alpha \nabla_{x_{t}} \log p(x_{t})」は、自然画像の確率分布\log p(x)を最大化する方向と逆の方向を示しています。
つまり、自然画像から意味のない画像に移動する向きの勾配です。
図で表すと下記のようなイメージです。

従って、勾配「- \alpha \nabla_{x_{t}} \log p(x_{t})」を加えていくことで、自然画像からノイズ画像に変化していきます。
自然画像からノイズ画像を作成することは、簡単に行うことができます。
そして下記の通り、各ステップごとの差分こそが、勾配「- \alpha \nabla_{x_{t}} \log p(x_{t})」となります。

したがって、全てのステップにおいて、同様の差分を学習することで、勾配「- \alpha \nabla_{x_{t}} \log p(x_{t})」を学習することができます。
感覚的理解のまとめ
拡散モデルをQ_\theta(x,t)とします。
xは入力される各stepごとのデータ点であり、tはステップ数を表します。
tステップ目のデータ点をx_tとし、完全なノイズ画像をx_T、自然画像をx_0とします。
学習時を考えます
このとき、x_{t-1}に対して、正規分布によるノイズを付与することで、x_tを作成します。
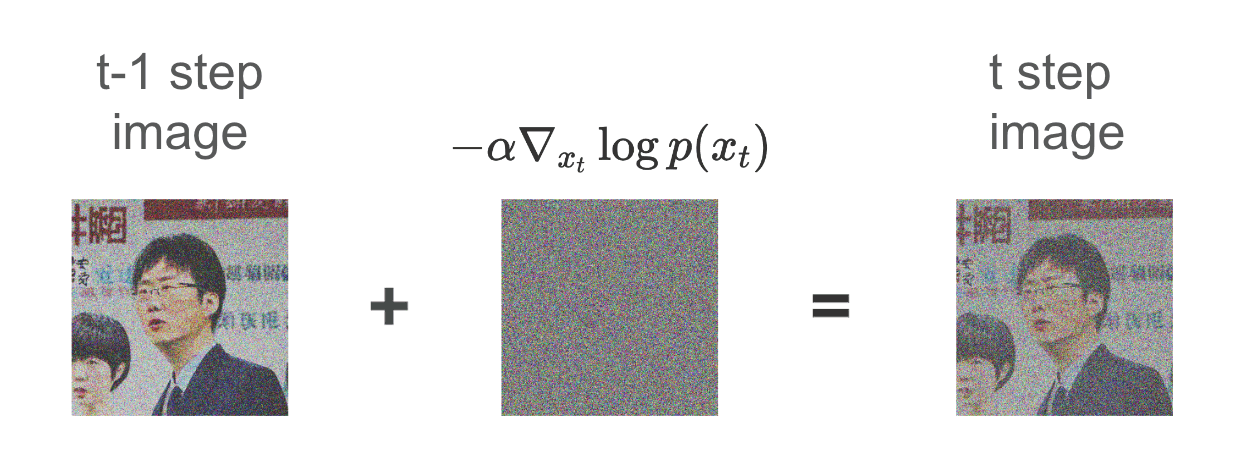
その後、ネットワークは
Q_\theta(x_t,t) = - \alpha \nabla_{x_{t}} \log p(x_{t})
となるように学習させます。
このときの損失関数を
Loss(\theta)、ネットワークの出力を
s_\theta(x_t,t)と再度書き直すと、下記の損失を最小化するように学習されます。
Loss(\theta) = |s_\theta(x_t,t) - (- \alpha \nabla_{x_{t}} \log p(x_{t}))|^2
推論時を考えます
推論時はこれまでに説明した通り、下記のようになります。
x_{t-1} = x_t - s_\theta(x_t,t)
この式を解釈すると、各stepごとにネットワークが出力した微小なノイズを、t step目の画像から減算(すなわちノイズを取り除く)ことで次のstepの画像が出力されています。
また式展開をすると下記のようになります。
x_{t-1} = x_t + \alpha \nabla_{x_{t}} \log p(x_{t})
この式で解釈すると、t step目の画像に対して、自然画像の確率分布の対数尤度
\log p(x_{t})を最大化する方向に更新をかけて次のstepの画像を出力していることがわかります。
したがって拡散モデルは下記のような特徴を持っているモデルということがわかりました。
拡散モデルQ_\theta(x_t,t)は、自然画像にノイズを付与する操作が、自然画像の確率分布の対数尤度を最大化する方向と逆方向であることを利用して、拡散モデルの出力s_\theta(x_t,t)を使って、下記の損失を最小化するように学習します。
Loss(\theta) = |s_\theta(x_t,t) - (- \alpha \nabla_{x_{t}} \log p(x_{t}))|^2
推論時には、各stepごとで、自然画像の確率分布の対数尤度を最大化する方向に、下記の式に基づいて入力データを誘導します。
x_{t-1} = x_t - s_\theta(x_t,t))
この式は展開すると下記のように表すことができ、
x_{t-1} = x_t + \alpha \nabla_{x_{t}} \log p(x_{t})
\Delta t \rightarrow 0, \; T = \inftyとして、無限回の更新を行うことを想定すると、それは下記のような常微分方程式を解くことと考えることもできます。
dx = \alpha \nabla_{x} \log p(x)dt
式変換
x_{t-1} = x_t + \alpha \nabla_{x_{t}} \log p(x_{t})
に対して、変化幅\Delta tを導入します。
上記式では1stepの更新のため、変化幅は1のため、下記のように式変形できます。
x_{t-1} = x_t + \alpha \nabla_{x_{t}} \log p(x_{t}) \Delta t
続いて普通に移項します
x_{t-1} - x_t = \alpha \nabla_{x_{t}} \log p(x_{t}) \Delta t
\Delta x_t = \alpha \nabla_{x_{t}} \log p(x_{t}) \Delta t
ここで\Delta t \rightarrow 0, \; T = \inftyとすると、
dx = \alpha \nabla_{x} \log p(x)dt
が成立します。
最後に、拡散モデル全体のパイプラインをまとめて、G_\theta(x)とすると、下記が成立します。
x_T \sim \mathcal{N}(0, I)
のとき、
ただし、
\mathcal{N}(0, I)は平均0、分散Iの標準正規分布(Iはx_Tと同じ次元の単位行列)
q(x)は大規模データセットDから推定された、自然画像の確率分布
G_\theta(x) = Q_\theta(x_T,T) \circ Q_\theta(x_{T-1},T-1) \circ ...... \circ Q_\theta(x_1,1)
Q_\theta(x_t,t) = x_t - s_\theta(x_t,t) = x_{t-1}
となります。
したがって、拡散モデルは、各stepごとに注目すると、対数尤度の最大化問題を微分方程式で解いており、パイプライン全体を見ると、標準正規分布からサンプリングされたデータ点x_Tを、ネットワーク全体の計算処理により変換し、自然画像の確率分布からサンプリングされたデータ点と一致させていると理解することができました。
補足(理論的な話)
ここまで、感覚的な話をしてきました。
ここからは数式的に理論的な話をしたいと思いますが、正直自分が書いても、本の焼き増しにしかならないし、本に書かれていた内容をそのまま書くのも良くないと思うので、簡単に紹介する程度にしておきます。
詳細と詳しい理論が知りたい方は、下記の本がおすすめです。
難しい数式なども非常に分かりやすく解説しており、とてもおすすめです。
拡散モデルを理解したい方は、全員購入するべきだと思います
拡散モデル データ生成技術の数理
下記の本は数式とまではいかなくても、ある程度コードを参照しながら大まかに理論を知りたい方に非常におすすめです。
上の本よりもとっつきやすく拡散モデルの理論に触れることができます。
ゼロから作るDeep Learning ❺ ―生成モデル編
損失関数の話
まず、上記で説明した損失関数を処理詳細に記載します。
まず、明示的スコアマッチングとして使われている損失関数は、上記で説明したものを近く、下記のように表されます。
J(\theta) = \mathbb{E}_{p_{\text{data}}(x)} \left[ \frac{1}{2} \left\| s_\theta(x) - \nabla_x \log p(x) \right\|^2 \right]
最初の\frac{1}{2}は、微分した時に係数が1になるように設定されています。
また最初の\mathbb{E}は期待値を表しています。
ここでいう期待値というのは、いわば、「たくさんの試行を行なった結果を平均してください」くらいに理解しておけば大丈夫です。
したがって、この式は前章で解説した損失関数と同じ式であることがわかると思います。
微分方程式の話
前章では、かなり雑な常微分方程式で解説をしていました。
実際に、拡散モデルで考えられている常微分方程式は下記になります。
(これは確率フローODEと呼ばれるものです。なぜこれが出てきたのかは本を読んでください)
d\mathbf{x} = \left[-\beta(t)\mathbf{x} - \alpha(t)\nabla_{\mathbf{x}} \log p(\mathbf{x})\right] dt
ただし、
です。
上記の式は、逆拡散課程(画像を生成する過程)においては、時刻の向きが前書の微分方程式と逆向きであるため、それを合わせると下記のようになります。
d\mathbf{x} = \left[\beta(t)\mathbf{x} + \alpha(t)\nabla_{\mathbf{x}} \log p(\mathbf{x})\right] dt
前章で提示していた常微分方程式と比較すると-\beta(t)\mathbf{x}が増えていると思います。これは拡散過程(ノイズ付与過程)において、単純にノイズを足し算しているわけではなく、入力データを減衰させていることが影響しています。
下記のようなイメージです。
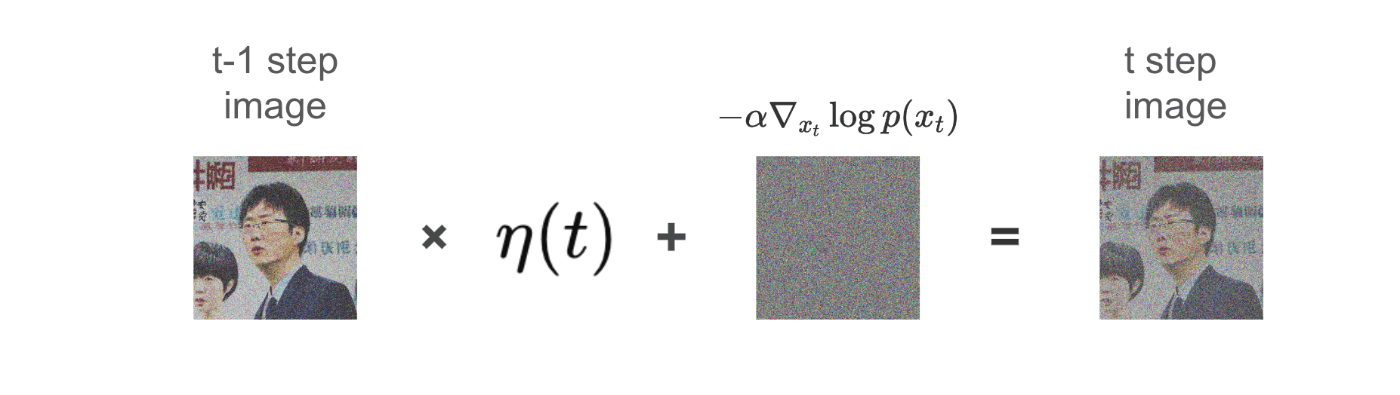
ただし、
なぜ、減衰させているのかというと、最終的なT step目に完全なノイズ画像にする必要があるからです。
拡散モデルの入力は標準正規分布からサンプリングされたノイズ画像を前提としています。しかしながら、自然画像を減衰させずに、ノイズを付与させると、生成されるノイズ画像は純粋な標準正規分布からサンプリングされたノイズ画像になりません。特に分散が大きくなってしまいます。
そこで、入力画像を各stepごとに減衰させて、ノイズを付与していくことで、最終的に標準正規分布からサンプリングされたノイズ画像と一致させる必要があります。
数式で整理すると、下記のようになります
q(x_t|x_{t-1}) := \mathcal{N}(x_t;\sqrt{\gamma_t}x_{t-1}, \delta_tI)
ただし、
0 < \delta_1 < \delta_2 < ...... < \delta_T < 1
となります。
また、上記をベースとすると、任意のサンプルx_tををx_0から解析的に求めることができます。
具体的には下記のように表せます。
q(x_t|x_0) := \mathcal{N}(x_t;\sqrt{\bar{\gamma_t}}x_0, \bar{\delta_t}I)
ただし、
\bar{\gamma_t} := \prod_{s=1}^{T} \gamma_t
\bar{\delta_t} := 1 - \bar{\gamma_t}
このとき、
q(x_T|x_0) = \mathcal{N}(x_T;\sqrt{\bar{\gamma_t}}x_{T-1}, \bar{\delta_t}I)
を考えた時に、
Tが十分大きければ、
\bar{\gamma_t} \approx 0, \bar{\delta_t} \approx 1
となるため、データ点
x_Tは平均0分散
Iの標準正規分布からサンプリングされた点となることがわかります。
このように、入力画像を減衰させて、ノイズを付与していく拡散過程があり、それをベースに逆拡散過程が定義されていため、下記のような微分方程式を解く必要があるということです。
d\mathbf{x} = \left[\beta(t)\mathbf{x} + \alpha(t)\nabla_{\mathbf{x}} \log p_t(\mathbf{x})\right] dt
そうなると、各stepでの処理は下記のように変わります。
x_{t-1} = x_t + \beta(t)x_t + \alpha(t)\nabla_{x_t} \log p(x_t)
イメージとしては、拡散過程にて減衰させられた入力データx_tを復元し(\beta(t)で復元率は制御)、その後拡散過程にて付与されたノイズを取り除いている形になります。
まとめ
今回は、拡散モデルに対して自分の理解を殴り書きしました。
本のネタバレにならないように、本の内容は基本的にはあまり書かないようにしました。
本記事を読んで、もっと拡散モデルの理論を知りたいと思ってくださると嬉しいです。
また、私は数学科ではないので、諸々謝っている部分があれば、ご指摘いただけますと幸いです。(私にもわかるように教えていただけますと嬉しいです)
次は、Samplerや、Flow Matchingなどについても勉強していこうと思います。
では読んでくださってありがとうございました!
参考
拡散モデル データ生成技術の数理
ゼロから作るDeep Learning ❺ ―生成モデル編
















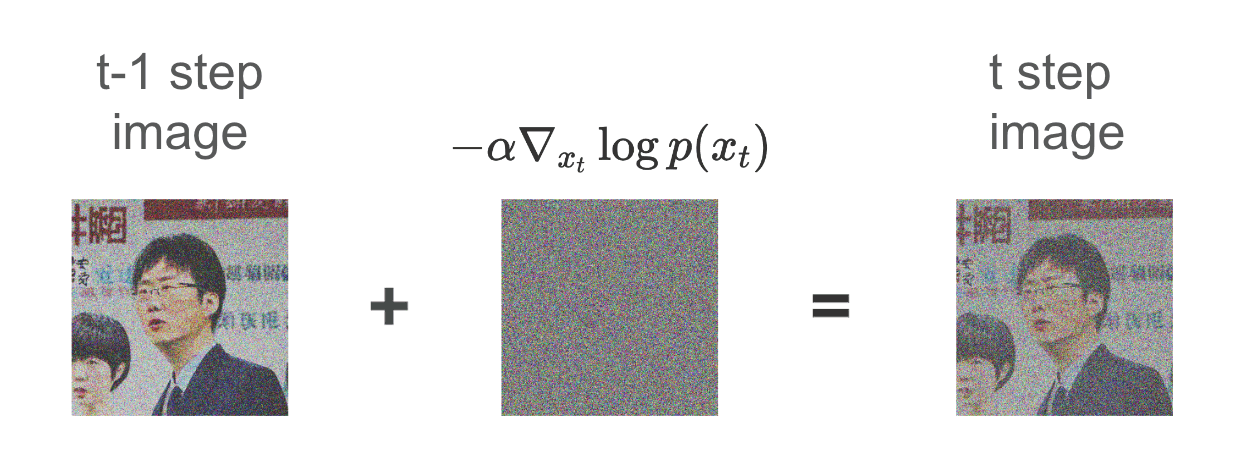
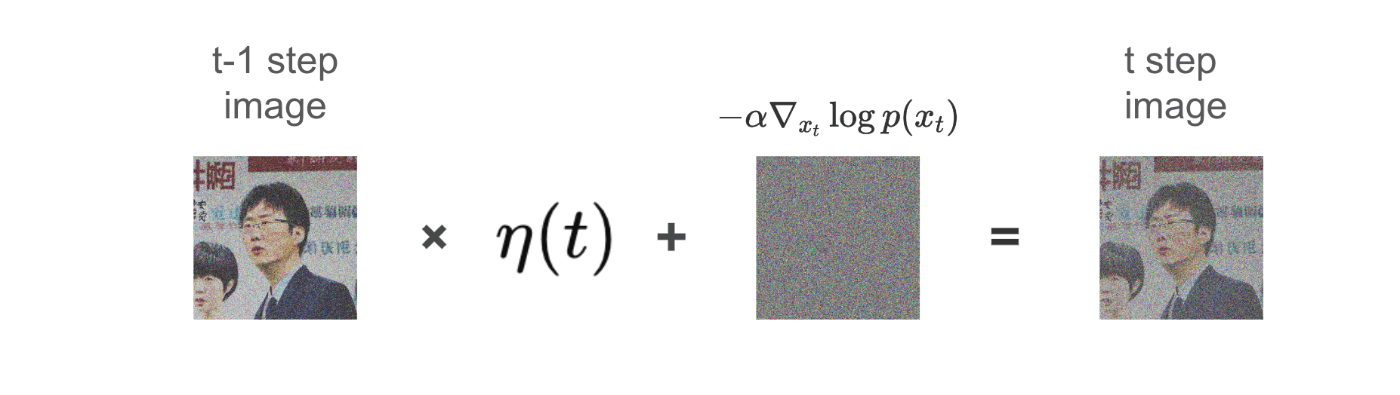
Discussion