LLMの性能における重要補題【Johnson–Lindenstrauss lemma】のお気持ち〜Attentionの数式理解を添えて〜

はじめに

本記事は、AI声づくり技術研究会 Advent Calendar 2024の17日目の記事です。
（音声合成関係ないテーマでごめんなさい・・・）

https://qiita.com/advent-calendar/2024/koeken

私の好きなyoutuberさんの一人として、「3Blue1BrownJapan」さんがいるのですが、その方の動画で面白い補題について触れていたため、今回はその内容について書きたいと思います。

該当の動画は「LLMはどう知識を記憶しているか | Chapter 7, 深層学習」です。

この動画の後半で「Johnson–Lindenstrauss lemma（ジョンソン-リンデンシュトラウスの補題）」という補題に触れており、興味深い実験も一緒にされております。

今回は、「Johnson–Lindenstrauss lemma」についての簡単な説明と、それが、現在のLLMに対してどう関わってくるのかを自分なりに考察したいと思います。

自分も色々調べたり勉強したりしておりますが、まだまだ完全に理解できていない部分があります。
間違っている内容があれば、こっそりと教えてください。

言葉遣いが厳密には間違っている、とかは結構あるとおもいますが、直感的な議論としては大きく外れてはないんじゃないかなと思っています。

参考文献

Johnson–Lindenstrauss lemmaについて

書籍：
Pythonではじめる教師なし学習 ―機械学習の可能性を広げるラベルなしデータの利用
（あまりJohnson–Lindenstrauss lemmaについては説明されていないですが、書籍の中で触れているだけで貴重だと思いました。実装方法の説明が軽く記載されています）

動画：
「LLMはどう知識を記憶しているか | Chapter 7, 深層学習」

Webページ：
Johnson–Lindenstrauss lemma:Wikipedia

johnson-lindenstrauss lemma preserves angles:mathoverflow

Dimensionality Reductions that Preserve Volumes and Distance to Affine Spaces, and their Algorithmic Applications

定理と補題について

書籍：
数学書の読みかた

Attensionについて

書籍：
大規模言語モデル入門

補題と定理とは

まず、そもそも補題（Lemma）とは何なのか？という点が疑問だと思います。

補題は、数学的な命題を表します。
命題とは、真偽が論理的に定まる主張のことを指します。
つまり、この部分だけ見れば、補題（Lemma）と定理（Theorem）は同じです。

しかし、補題と定理、それぞれの役割や目的には違いがあります。

補題は、主に、他の命題の証明を助けるために用いられる補助的な命題です。
つまり、補題が出てきた場合は、その後の重要な定理を導くために、この補題が使われるという意味です。

一方で、定理は、数学的な研究や応用の中心的な命題で、重要性や一般性を持つものです。定理は補題に比べて理論や応用上の重要性が高いものになります。

今回の記事で取り扱うのは、「Johnson–Lindenstrauss lemma」なので、補題の方になります。

こうかくと、重要性の低い命題のように見えますが、そうではありません。
補題として証明された命題の中には、のちに、とても重要な命題だとわかったものもあり、そのような補題は特定の名前で呼ばれることが多いです。

「Johnson–Lindenstrauss lemma」は補題でありながら、数学的にも実用的にも定理に匹敵する、非常に重要な命題の一つです。

Johnson–Lindenstrauss lemma

まずは、wikiに記載されている定義をそのまま書くことにします。

任意の$n$個の点集合$\{x_1, x_2, \dots, x_n\}$が$\mathbb{R}^d$内に存在し、$k > \frac{8 \ln n}{\varepsilon^2}$となる$k$が存在するとする。
このとき、任意の$0 < \epsilon < 1$に対して、次を満たす低次元空間への線形写像$f : \mathbb{R}^d \to \mathbb{R}^k$が存在する：

$$(1 - \epsilon)\|x_i - x_j\|^2 \leq \|f(x_i) - f(x_j)\|^2 \leq (1 + \epsilon)\|x_i - x_j\|^2 \quad \forall i, j$$

つまり、Johnson–Lindenstrauss lemmaは、高次元空間に存在する点の集合を、距離をほぼ保ったまま低次元空間に埋め込むことができることを保証する数学的な定理です。

式を見てみましょう。
$\|x_i - x_j\|^2$は、$d$次元空間での、任意の点($\forall i, j$)同士の距離を表します。
$\|f(x_i) - f(x_j)\|^2$は、$k(<d)$次元空間での、任意の点同士の距離を表します。

したがって、

$$(1 - \epsilon)\|x_i - x_j\|^2 \leq \|f(x_i) - f(x_j)\|^2 \leq (1 + \epsilon)\|x_i - x_j\|^2 \quad \forall i, j$$

上記の式は、写像$f$による次元削減の前後において、2点間の2乗距離の相対誤差が$\varepsilon$ 以下である、すなわちそんなに距離が変わらないということを示しています。

距離が変わらないとは？

2点間の距離が変わらないというのは、直感に反します。
例えば、私は以前、主成分分析についての記事を書きました。

https://zenn.dev/asap/articles/ff8f34d19ca6a4

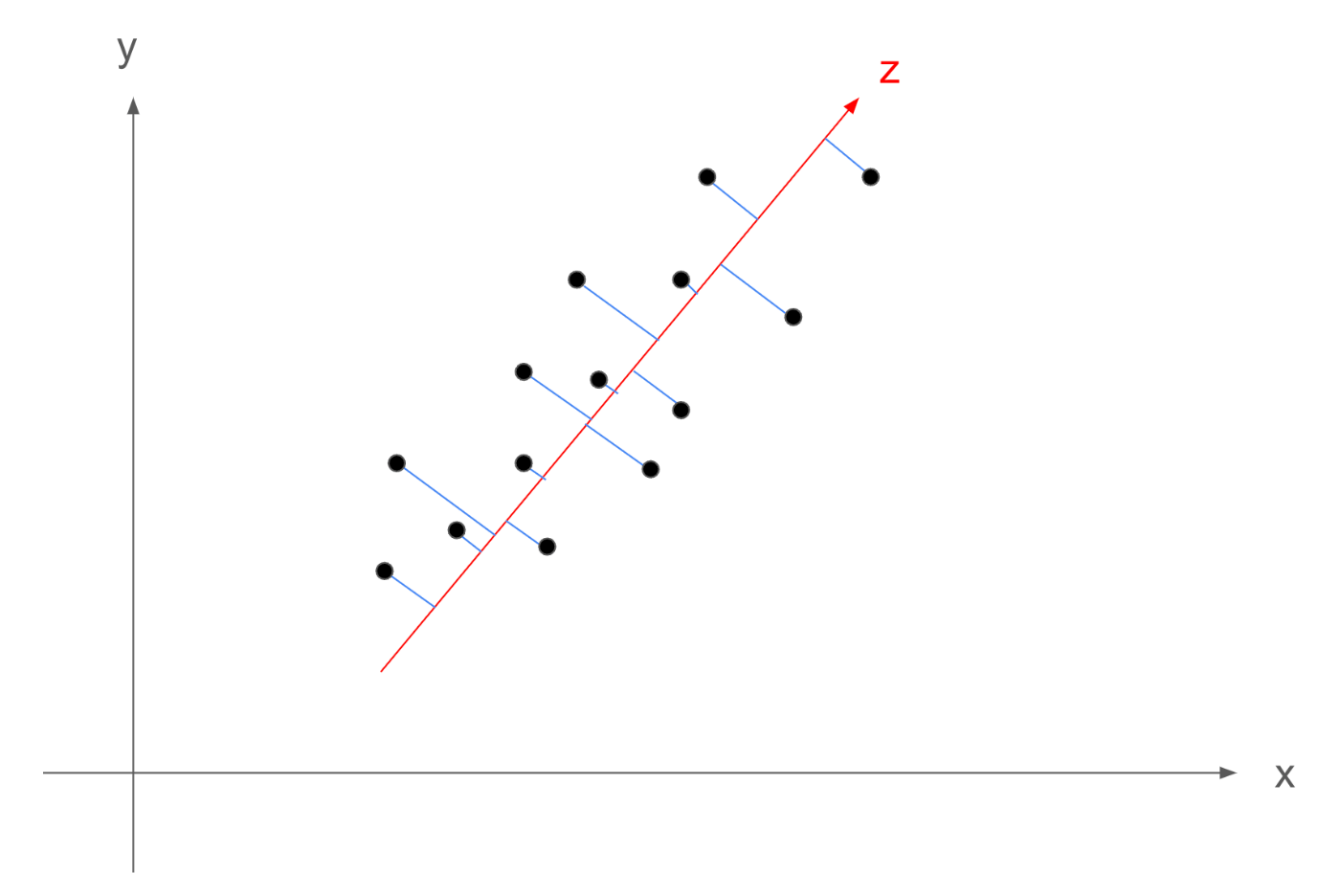
記事中の図の通り（ここでは2次元の図ですが）、次元を圧縮する場合、基本的には、点同士の距離は近くなってしまうことが多いです。

そして、「点同士の距離が短くなってしまう」というのは、情報が削られるという意味です。

次元を削減することで、情報が削られるというのは直感通りです。

しかし、Johnson–Lindenstrauss lemmaでは、高次元空間において、次元を削減しても、2点間の距離は相対誤差$\epsilon$の範囲内で距離が保たれる。
つまり、情報を（ほとんど）保持できる（ような写像$f$が存在する）と言っているわけです。

これが、Johnson–Lindenstrauss lemmaが直感に反しており、面白いところです。

距離が変わらないなら、区別・学習ができるということ

距離が変わらないと言うことは、次元削減前後で、異なるクラス間の点を区別する難易度が大きく変わらないことを意味します。

例えば、SVM（サポートベクターマシン）のような機械学習モデルを考えます。SVMはクラス間のマージンを最大化する分離超平面を引き、クラス分類を行います。

Johnson–Lindenstrauss lemmaでは、次元削減前後で、任意の2点間の距離が相対的に保たれることを示しています。
したがって、SVMを考えたときに、次元削減前後で、クラス間のマージンを最大化するような分離超平面を引く難易度が大きく変わらないと言えます。

距離が変わらない=角度が変わらない

Johnson–Lindenstrauss lemmaでは、高次元空間において、「任意」の2点間の距離が、次元削減後もほとんど変わらないような写像$f$が存在することを示していました。

任意の2点間の距離が変わらないということは、ある3点をとってきた時に、その3点が作る三角形の3辺の長さが、次元削減前後で、ほとんど変わらないことを示しています。
「3辺の辺の長さがほとんど変わらない」ということは、余弦定理により、その3点が作る三角形の内角が、次元削減前後で変わらないことを示しています。

詳細は下記をご覧ください。
https://mathoverflow.net/questions/356213/johnson-lindenstrauss-lemma-preserves-angles

https://www.stat.purdue.edu/~yuzhu/stat598m3/Papers/dimensionalityreductions.pdf

つまり、Johnson–Lindenstrauss lemmaでは、高次元空間において次元削減前後で、点間の距離と、角度を保存するような写像$f$が存在することを示しています。

角度が変わらない=基底ベクトルが保存される

Johnson–Lindenstrauss lemmaでは、高次元空間において、適切な写像$f$による次元削減前後で、点間の距離と、角度を保存することを示しています。

すなわち、高次元空間における基底ベクトルも、次元削減後に（相対誤差$\epsilon$の範囲内で）保存されているはずです。
具体的にいうと、1,000万次元の基底ベクトルは、長さが1のものに限定すると、1,000万個のベクトルが存在するはずです。
それらの基底ベクトルは、互いに直交しているはずです。

Johnson–Lindenstrauss lemmaでは、適切な写像$f$を用いて、低次元空間（例えば10万次元）に次元削減しても、1,000万次元の基底ベクトルの角度が、ほとんど保存されるということを示しています。

実験

では、一旦、実験をしてみたいと思います。
ここでの実験は、参考にした動画内で実施していた実験と同様の実験になります。
（コード含め動画に記載されていたものを利用させていただいております）
詳細に知りたい方は動画をご覧ください。

上記の動画では、ランダムな10,000個の100次元ベクトルを用意して、それらのベクトルが89度から91度の範囲にほとんど収まるようなことを示しています。

実際のコード

実際のコードは下記をご覧ください。（興味がある方は実行してみてください）
コード自体は、動画にちょろっと映ったコードを元に記載しております。
加えて、Google ColabのGPUが利用して高速化できるようにしています。

https://github.com/personabb/colab_AI_sample/blob/main/colab_Johnson–Lindenstrauss_lemma_sample/Johnson–Lindenstrauss_lemma2.ipynb

下記の実行結果は、上記のコードを最後まで実行すると得られます。

実行結果

まず、下記に、最適化前のランダムに作成した10,000個の100次元ベクトルから2つの組のなす角度をヒストグラムとして表示すると下記になります。（組の数は99,990,000組）

10,000個のベクトルが100次元空間の中ですべて直交した場合、10,000次元の基底ベクトルの構造が100次元に次元削減しても保存されたと言うことができます。

実際に、最適化を250回実施した後のヒストグラムは下記になります。

上記の通り、89度から91度の範囲内に、ほぼすべてのベクトルの組が入っています。
どの程度入っているかは、下記の通りです

全データ数: 99990000
89度から91度の範囲にあるデータの個数: 98294342
割合：98.30%

したがって、全組のうち98%以上の組み合わせにおいて、ベクトルのなす角が、89度から91度の範囲内に入っていることがわかります。

以上のことから、100次元空間において、10000次元空間の基底ベクトルの構造が保存されていることがわかります。

完全に直交しているわけではないですが、89-91度の範囲内に収まっており、ほとんど直交していると言えると思います。
今後、これを準直交と呼ぶことにします。

上記の実験は、あくまでJohnson–Lindenstrauss lemmaのイメージを把握するための実験です。
実際には、Johnson–Lindenstrauss lemmaによって「100次元空間において、10000次元空間の基底ベクトルの構造が保存される」というのは言い過ぎです。

動画にケチをつけるようであれですが、正直、上記の実験結果はJohnson–Lindenstrauss lemmaを示唆するには不十分です。

しかしながら、考えている次元数を、もっとずっと大きくすれば、この議論は成立します。
（Google ColabのRAMでは、これ以上大きな次元での計算は難しいです。元動画でも計算量を考慮して小さめの次元でイメージを共有するために実施していたのかなと思います。）

角度が準直交していることの重要性

さて、ここまでの議論で、Johnson–Lindenstrauss lemmaにおいて、高次元の基底ベクトルが、次元削減のあとでも、準直交の形で構造が保たれることがわかりました。

角度が直交しているとは？

2次元の平面を考えてみましょう。

横軸は、性別を表しており、右に行くと男性、左に行くと女性を示します。
縦軸は、年齢を表しており、上にいくと大人、下に行くと子供を示します。
そのような平面を考えた時に、(男性、女性、男子、女子)の単語を平面に埋め込んだ場合、下記のようなイメージになることが想定されます。

つまり、単語をベクトルとして考えた時に、その平面の軸は、単語を構成する意味を表します。（つまり性別や年齢）

その上で、この2軸にそれぞれ直行している3軸目として、「家族度合い」を表すような軸を追加した場合、「お父さん」や「お母さん」と言った単語も表現ができるようになります。

このように、単語をベクトルとして表現するとき、
全体として次元数分の意味を表現することができる
ベクトル空間上での一点として表現することができます。

つまり、100次元空間上では100の意味を表現でき、10,000次元の空間上では10,000の意味を表現することができます。

これは、
すべての軸（基底ベクトル）が互いに直交している
から成り立っています。

もし、すべての規定ベクトルと直交していないベクトルを考えた時、そのベクトルは基底ベクトルの線型結合で表現することができる（一次従属）ため、基底ベクトルが持つ意味以上の概念を持つことはできないということです。

基底ベクトルが準直交で構造が保たれるとは

NNは、データとパラメータ同士の内積計算をしている

では、この基底ベクトルが準直交で構造が保たれるというのが何が良いのかを考えます。
例えば、全結合層を考えると下記のような線形演算が含まれます。

$$Z_2 = W_1X_1 = \begin{pmatrix} w_{11}^{(1)} x_{1}^{(1)} + w_{21}^{(1)} x_{2}^{(1)} + w_{31}^{(1)} x_{3}^{(1)} + w_{41}^{(1)} x_{4}^{(1)} + w_{51}^{(1)} x_{5}^{(1)} \\ w_{12}^{(1)} x_{1}^{(1)} + w_{22}^{(1)} x_{2}^{(1)} + w_{32}^{(1)} x_{3}^{(1)} + w_{42}^{(1)} x_{4}^{(1)} + w_{52}^{(1)} x_{5}^{(1)} \\ w_{13}^{(1)} x_{1}^{(1)} + w_{23}^{(1)} x_{2}^{(1)} + w_{33}^{(1)} x_{3}^{(1)} + w_{43}^{(1)} x_{4}^{(1)} + w_{53}^{(1)} x_{5}^{(1)} \\ w_{14}^{(1)} x_{1}^{(1)} + w_{24}^{(1)} x_{2}^{(1)} + w_{34}^{(1)} x_{3}^{(1)} + w_{44}^{(1)} x_{4}^{(1)} + w_{54}^{(1)} x_{5}^{(1)} \\ \end{pmatrix}$$

ただし、$Z_2$は次の層の活性化関数入力前のベクトルです。
また、バイアスは考えず、$W_1$と$X_1$は下記のように考えます。

$$W_1 = \begin{pmatrix} w_{11}^{(1)} & w_{21}^{(1)} & w_{31}^{(1)} & w_{41}^{(1)} & w_{51}^{(1)} \\ w_{12}^{(1)} & w_{22}^{(1)} & w_{32}^{(1)} & w_{42}^{(1)} & w_{52}^{(1)} \\ w_{13}^{(1)} & w_{23}^{(1)} & w_{33}^{(1)} & w_{43}^{(1)} & w_{53}^{(1)} \\ w_{14}^{(1)} & w_{24}^{(1)} & w_{34}^{(1)} & w_{44}^{(1)} & w_{54}^{(1)} \end{pmatrix}$$

$$X_1 = \begin{pmatrix} x_{1}^{(1)} \\ x_{2}^{(1)} \\ x_{3}^{(1)} \\ x_{4}^{(1)} \\ x_{5}^{(1)} \end{pmatrix}$$

ここで、k行目に着目すると

$$z_{k}^{(2)} = w_{1k}^{(1)} x_{1}^{(1)} + w_{2k}^{(1)} x_{2}^{(1)} + w_{3k}^{(1)} x_{3}^{(1)} + w_{4k}^{(1)} x_{4}^{(1)} + w_{5k}^{(1)} x_{5}^{(1)} = \langle w_{k}^{(1)}, X_{1} \rangle$$

となり、内積によって表現できることがわかります。

上記では全結合層（の線形変換部分）で考えましたが、CNNの畳み込みでも同じです。

畳み込みは下記の式で表現できます。

$$Z_{i,j} = \sum_{m=0}^{M-1} \sum_{n=0}^{N-1} W_{m,n} \cdot X_{i+m, j+n}$$

ただし、簡単のために1チャンネルを想定しており、また、

• $Z_{i,j}$は出力特徴マップ（活性化関数入力前）の位置$(i,j)$の値
• $X_{i,j}$は入力特徴マップの位置$(i,j)$の値(サイズ$H \times W$)
• $W_{i,j}$は畳み込みカーネルの位置$(i,j)$の値(サイズ$M \times N$)

となります。

そして、上記は2次元表示なのでわかりにくいですが、上記の表現もまた、$X$と$W$の内積になっていることがわかると思います。

（補足：この記事内では、ユークリッド内積（高校で習う一般的な内積）のことを内積と呼んでいます）

内積は類似度を判定する

内積は下記の形で表現されます。
ただし、$\mathbf{a}$と$\mathbf{b}$はベクトルです。

$$\langle \mathbf{a}, \mathbf{b} \rangle = \sum_{i=1}^n a_i b_i = \|\mathbf{a}\| \|\mathbf{b}\| \cos\theta$$

前節で議論していた内積は、主に、$\langle \mathbf{a}, \mathbf{b} \rangle = \sum_{i=1}^n a_i b_i$の形です。

そして、内積であるならば、$\langle \mathbf{a}, \mathbf{b} \rangle = \|\mathbf{a}\| \|\mathbf{b}\| \cos\theta$の形も成立するはずです。

ここで重要なのは、$\cos\theta$です。
$\cos\theta$は$\theta = 90^\circ$の時に$0$になり、$\theta = 0^\circ$の時に$1$、$\theta = 180^\circ$の時に$-1$になる関数です。

すなわち、内積は、下記のような性質があります。

• 2つのベクトルが同じ方向を向いている場合（$\theta = 0^\circ$）、内積は最大値$\|\mathbf{a}\| \|\mathbf{b}\|$をとる
  • この場合、2つのベクトルは概念として近い
• 2つのベクトルが逆方向を向いている場合（$\theta = 180^\circ$）、内積は最小値$-\|\mathbf{a}\| \|\mathbf{b}\|$をとる
  • この場合、2つのベクトルはある概念として正反対
• 2つのベクトルが直交している場合（$\theta = 90^\circ$）、内積は0になる
  • この場合。2つのベクトルはどの概念を考えても、全くの無関係

これにより、内積とは、2つのベクトルの方向が類似しているかどうかにより、値が変わる指標であると言えます。

したがって、2つのベクトルの方向が類似しているかどうかは、$\cos\theta$の値で判断できて、それをcos類似度とよんだりもします。

内積の場合は、厳密にはベクトルの大きさも入ってくるため、内積が大きいから2つのベクトルが類似しているとは必ずしも言えないですが、大まかには同様の解釈をすることができます。

改めて角度が準直交している=次元以上の表現能力を得る

さて、Johnson–Lindenstrauss lemmaに戻ります。

Johnson–Lindenstrauss lemmaは、適切な写像$f$を用いて、次元削減を行った場合、高次元空間での基底ベクトルが、次元削減のあとでも、準直交の形で構造が保たれることを主張しています。

実際に、前章の「実験」では、100次元のベクトル空間において、10,000個のベクトルのなす角のペアのうち、98.3%の組が準直交していました。

準直交の角度を$\theta'$とすると、$\|\cos\theta'\| < 0.0175$となります。
（これは$\cos 89^\circ = 0.01745...$となるからです）

すなわち、準直交している場合、内積の値は、ノルム積に0.01程度の値がかけられることになるため、非常に小さい値になります。

つまり、とても大雑把にいうと、準直交しているベクトルにおいて、その内積を計算した結果は0に近い値が出力されることが期待されます。

上記の話を整理すると、
100次元ベクトル空間において、10,000個のベクトルのほとんどは、互いに準直交していると言えます。
準直交している場合は、内積の結果が0に近くなるため、100次元空間には、約10,000もの独立した表現を組み込むことができていることになります。

これは、100次元空間のすべての軸に対して、準直交のであるベクトルを追加で用意することができることを示しており、結果として、100次元空間に、100以上の意味の概念を与えることができる直感的な説明です。

LLMではどうなのか

さて、ここまでで、Johnson–Lindenstrauss lemmaについての説明と、CNNや全結合層では内積計算をしているため、角度が準直交で保存されることの重要性がわかっていただけたかと思います。

では、LLMではどうなのかについて、記載しようと思います。
LLMではTransfomerと呼ばれる構造が利用されています。

Transfomerは大雑把に分割するとSelf-Attensionと全結合層によって構成されます。
全結合層は上述したため、ここではSelf-Attensionに絞って解説します。

全結合層（Feed Forward Network）において、Johnson–Lindenstrauss lemmaにより、次元数以上の概念を埋め込むことについては、参考にした動画にも詳しく説明されておりますので、そちらもご覧ください。

「LLMはどう知識を記憶しているか | Chapter 7, 深層学習」

Self-Attensionとは

数式の提示

Self-Attensionは下記で表現されます。

$$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^\top}{\sqrt{m}}\right)V$$

ここでいう$Q,K,V$は入力されたテキストのtokenの特徴量表現（の線形変換）だと思ってもらっても、大雑把には問題ないです。

私たちが入力として与えたプロンプトをベクトル化したものを$X$とすると、

$$X = \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3}\\ \vdots \\ x_{n} \end{pmatrix}$$

$$x_{i} = \{c_1^i,c_2^i,c_3^i,\cdots,c_m^i \}$$

であり、

$$Q=XW^Q, K=XW^K, V=XW^V$$

という関係性があります。
ここで、$X$はtokenをベクトル化したものの、時系列表現ベクトルで、$x_{i}$は各tokenの埋め込み表現（$m$次元）です。

簡単のために、Self-Attensionの最初の層を考えました。

2層目以降の場合は、前段のSelf-Attenison層により、類似度の高いtoken同士の結びつきが強くなり、Feed Forward　Network（全結合層）にて、新たな概念を獲得した状態（つまり文章理解度が多少上がった状態のベクトル）で同じ処理が行われるだけです。

部分ごとに解説

$Q=XW^Q, K=XW^K, V=XW^V$より、$Q,K,V$は、入力$X$の線形変換であり、線形変換では大きく構造を壊すような変換にはならないため、大雑把に同じようなベクトルを持っていると考えてください。

その場合、下記のSelf-Attensionに対して、次の順番に説明していきます。

$$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^\top}{\sqrt{m}}\right)V$$

• $QK^\top$が入力tokenの内積（類似度）を計算していること
• $\sqrt{m}$は、$m$次元のtokenの内積計算後の結果の標準化をするパラメータ
• $\text{softmax}$により、正規化
• 類似度マップと$V$の行列積を実施する。これは全範囲畳み込みに相当する

類似度マップの計算

まずは

$QK^\top$が入力tokenの内積（類似度）を計算していること

を考えます。

$Q=XW^Q, K=XW^K$なので、

$$Q = \begin{pmatrix} q_{1} \\ q_{2} \\ q_{3} \\ \vdots \\ q_{n} \end{pmatrix}$$

$$q_{i} = \{q_{c1}^i,q_{c2}^i,q_{c3}^i,\cdots,q_{cm}^i \}$$

$$K = \begin{pmatrix} k_{1} \\ k_{2} \\ k_{3} \\ \vdots \\ k_{n} \end{pmatrix}$$

$$k_{i} = \{k_{c1}^i,k_{c2}^i,k_{c3}^i,\cdots,k_{cm}^i \}$$

となります。

したがって、

$$QK^\top = \begin{pmatrix} q_{1} \\ q_{2} \\ q_{3} \\ \vdots \\ q_{n} \end{pmatrix} \begin{pmatrix} k_{1} k_{2} k_{3} \cdots k_{n} \end{pmatrix} = \begin{pmatrix} \langle q_{1}k_{1}\rangle & \langle q_{1}k_{2}\rangle & \langle q_{1}k_{3}\rangle & \cdots & \langle q_{1}k_{n}\rangle \\ \langle q_{2}k_{1}\rangle & \langle q_{2}k_{2}\rangle & \langle q_{2}k_{3}\rangle & \cdots & \langle q_{2}k_{n}\rangle \\ \langle q_{3}k_{1}\rangle & \langle q_{3}k_{2}\rangle & \langle q_{3}k_{3}\rangle & \cdots & \langle q_{3}k_{n}\rangle \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \langle q_{n}k_{1}\rangle & \langle q_{n}k_{2}\rangle & \langle q_{n}k_{3}\rangle & \cdots & \langle q_{n}k_{n}\rangle \\ \end{pmatrix}$$

すなわち、

$$\{QK^\top\}_{i,j} = \langle q_{i}k_{j}\rangle$$

と書けます。
したがって、$i$番目のtokenと$j$番目のtokenとの内積を計算しています。

前述しましたが、内積というのは類似度になります。

$$\langle q_{i}k_{j}\rangle = q_{c1}^ik_{c1}^j + q_{c2}^ik_{c2}^j + \cdots + q_{cm}^ik_{cm}^j = \|q_{i}\| \|k_{j}\| \cos\theta$$

下記の通り、2つのベクトル$q_{i}, k_{j}$が、

• 同じ方向を向いている場合（$\theta = 0^\circ$）、内積は最大値$\|q_{i}\| \|k_{j}\|$をとる
• 逆方向を向いている場合（$\theta = 180^\circ$）、内積は最小値$-\|q_{i}\| \|k_{j}\|$をとる
• 直交している場合（$\theta = 90^\circ$）、内積は0になる

となります。

したがって、$\{QK^\top\}_{i,j}$は、大雑把に、2つのベクトル$q_{i}, k_{j}$が類似していれば、大きく、逆行していれば小さくなります。

標準化

続いて、$\frac{QK^\top}{\sqrt{m}}$を考えます。

$QK^\top$は上述しました。
それを、$\sqrt{m}$で割っています。

なぜ割るかというと、標準化と同じです。
下記で解説します。

たとえば、$q_{ct}^i, k_{ct}^j$を考えた時に、それぞれが独立で、分散$\sigma_q^2, \sigma_k^2$の確率変数と仮定すると、その積である$q_{ct}^ik_{ct}^j$の分散は、線形性により$\sigma_q^2\sigma_k^2$となります。

2つの確率変数の平均が0であり、独立である場合、分散は下記が成立します。

$$\mathrm{Var}(XY) = \mathrm{Var}(X)\mathrm{Var}(Y)$$

その上で、内積を考えるので、下記のように$m$次元分の総和をとります。

$$\langle q_{i}k_{j}\rangle = q_{c1}^ik_{c1}^j + q_{c2}^ik_{c2}^j + \cdots + q_{cm}^ik_{cm}^j$$

それぞれが分散$\sigma_q^2\sigma_k^2$で$m$次元の総和をとった場合、$\langle q_{i}k_{j}\rangle$の分散は$m\sigma_q^2\sigma_k^2$となります。

分散は下記が成立します。

$$\mathrm{Var}(X + Y) = \mathrm{Var}(X) + \mathrm{Var}(Y)$$

したがって、

$$\mathrm{Var}(QK^\top) = m\sigma_q^2\sigma_k^2$$

となります。
であるから、

$$\mathrm{Var}\left(\frac{QK^\top}{\sqrt{m}}\right) = \frac{1}{\sqrt{m}^2} \times \mathrm{Var}(QK^\top) = \frac{1}{\sqrt{m}^2} \times m\sigma_q^2\sigma_k^2 =\sigma_q^2\sigma_k^2 = \mathrm{Var}(q_{ct}^ik_{ct}^j)$$

より、各特徴量の分散の積にまでスケールを落とす効果があることがわかります。
逆にいうと、このスケールダウンを行わない場合、分散が次元数$m$倍だけ大きくなってしまいます。

Attensionの計算において、このスケーリングを行わないと、次元数が多い場合に、内積計算時に足し合わされる項が多いので、その分値が大きくなってしまい、Softmaxの計算が不安定になります。

この段階で$\sqrt{m}$で割ることによって、この分散が次元数$m$に依存しない値になるため、どれだけ特徴量の次元数$m$が増えようと、Softmaxの学習の不安定さがなくなります。

Softmaxによる正規化

続いて、$\text{softmax}\left(\frac{QK^\top}{\sqrt{m}}\right)$を考えます。

ここでは、最終的に類似度マップを作成したいです。

$\frac{QK^\top}{\sqrt{m}}$では、内積計算後に分散のスケーリングを行っています。
その上で、Softmaxをかけています。

Softmaxは、行方向もしくは列方向に対して、すべての要素が0以上かつ、総和が1になるように変換してくれます。
すなわち、値を確率として評価できるようになります。

今回、$\text{softmax}\left(\frac{QK^\top}{\sqrt{m}}\right)$は行列積の左側になることが想定されるため、行ベクトルに対して、Softmaxを適応します。

したがって、ある行に着目したときに、内積の大小関係はそのままに、確率として表現できるように変換してくれます。

下記のように、ある行$i$に着目すると下記のように書けます。

$$\text{softmax}\left(\frac{QK^\top}{\sqrt{m}}\right)_i = \begin{pmatrix} \alpha_{i1} &\alpha_{i2} &\alpha_{i3}& \cdots &\alpha_{in} \end{pmatrix}$$

ただし、

$$\alpha_{ij} = \frac{e^{\langle q_{i}k_{j}\rangle}}{\sum_{s=1}^n e^{\langle q_{i}k_{s}\rangle}} ,\quad \sum_{j=1}^n \alpha_{ij} = 1$$

です。

つまり、$\alpha_{ij}$というのは、$i$番目のtokenと$j$番目のtokenの類似度を確率として表現した値になります。

類似度マップとVとの全範囲畳み込み

最後です。

$$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^\top}{\sqrt{m}}\right)V$$

を考えます。

ここでは、ここまでで作成した類似度マップと、入力tokenの（線形変換）の値$V$の行列積を計算します。
実はこれは、全範囲をカバーするカーネルを持つ畳み込みを行っています。

詳しく記載します。

まず、最後の式は下記のように書けます。

$$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^\top}{\sqrt{m}}\right)V = \begin{pmatrix} \alpha_{11} &\alpha_{12} &\alpha_{13}& \cdots &\alpha_{1n} \\ \alpha_{21} &\alpha_{22} &\alpha_{23}& \cdots &\alpha_{2n} \\ \alpha_{31} &\alpha_{32} &\alpha_{33}& \cdots &\alpha_{3n} \\ \vdots & \vdots & \ddots & \vdots \\ \alpha_{n1} &\alpha_{n2} &\alpha_{n3}& \cdots &\alpha_{nn} \\ \end{pmatrix} \begin{pmatrix} v_{1} \\ v_{2} \\ v_{3} \\ \vdots \\ v_{n} \end{pmatrix}$$

ただし、

$$\alpha_{ij} = \frac{e^{\langle q_{i}k_{j}\rangle}}{\sum_{s=1}^n e^{\langle q_{i}k_{s}\rangle}} ,\quad \sum_{j=1}^n \alpha_{ij} = 1$$

$$V=\begin{pmatrix} v_{1} \\ v_{2} \\ v_{3} \\ \vdots \\ v_{n} \end{pmatrix} , \quad v_{i} = \{v_{c1}^i,v_{c2}^i,v_{c3}^i,\cdots,v_{cm}^i \}$$

となります。

ここで前節と同様に、ある行$i$に着目して考えます。

$$\text{Attention}(Q, K, V)_i = \alpha_{i1}v_{1} + \alpha_{i2}v_{2} + \alpha_{i3}v_{3} + \cdots + \alpha_{ii}v_{i} + \cdots + \alpha_{in}v_{n} = \sum_{j=1}^n \alpha_{ij}v_{j}$$

ここで、$\sum_{j=1}^n \alpha_{ij}v_{j}$というのは、$i$番目のtokenと$j$番目のtokenの類似度による$j$番目のtokenの特徴量の重みづけ和が、次の層の$i$番目のtokenの特徴量になります。

つまり、ある特定のtoken$v_{i}$に注目したときに、そのtokenと、その他の全てのtokenの特徴量との類似度マップを用意し、その類似度マップと入力tokenとの重みづけ和を計算します。
そして、注目するtokenと変更（$v_{i+1}$）して、同様の処理を行うため、これはカーネルサイズが画像サイズになる（パディングなし）畳み込みに対応します。

たとえば、ある特定のtoken$v_{i}$と、$v_{3}$や$v_{6}$がかなり類似していたとして、
その他のtokenとは全く類似していなかった場合は、$i$番目のtokenの出力特徴量は$v_{i}$と、$v_{3}$、$v_{6}$の特徴の重み付け和になります。
そして、次の層では、類似度の高いtokenの特徴量の情報を得られた$v'_{i}$がまた類似度の高い他のtokenとの重み付け話が計算されます。

これを繰り返すことで、transfomerでは、あるtokenには文章全体の概念が、ベクトルとしてだんだん埋め込まれていくことで文章を処理することができます。

LLMとJohnson–Lindenstrauss lemma

さて、Attensionの計算を見ていく中で、内積や類似度というのがたくさん出てきました。
この内積や類似度は、あくまでベクトル同士のなす角によって計算されます。（$\cos\theta$として）

最初に見た通りJohnson–Lindenstrauss lemmaでは高次元空間においては、次元の数以上に準直交という形の構造を持つベクトルを持つことができます。
また、ベクトルが直交しているというのは、概念として合っているわけでも正反対というわけでもなく、全く関係ない概念であるということでした。

以上のことを考えると、仮説ではありますが、LLMにおいて、LLMが持っている次元以上に、準直交という形で、全く関係ない概念を処理することができるということが示唆されます。

まとめ

ここまで読んでくださってありがとうございます。
まだまだ勉強中の身ではございますが、忘れないうちに現時点での理解をアウトプットしました。

皆様の理解の一助になれば幸いです。