【DB】閉世界仮説と正規化理論

はじめに
バックエンドでお馴染みのDBの正規化ですが、最近ではフロントエンドでも正規化を扱うことが増えてきました。
フロントエンドではVueでもReactでもstateという形で情報を保持するわけですが、このstateが最近は肥大化してきており、実務の現場ではこのstateの正規化を行う必要があります。
そういうわけで開発を進める上ではフロントエンド、バックエンドに関わらず正規化理論は知っておかなければいけない基礎知識です。
ところで、よく使われる技術というものは背景に数学の堅牢な理論が存在していることが少なくありません。
例に漏れず、正規化理論もまた論理学の延長線上に存在している理論になります。
今回は、一般的な見方とは少し異なる視点から、正規化理論のバックボーンを追っていきます。
第1項 集合とその要素の絶対条件
それでは順に見ていきましょう。
まず初めに、リレーショナル型DBでお馴染みのテーブルという考え方は集合論を背景として確立された技術です。
高校の数学I・Aの時間で触れたことがある方も多いと思いますが、もういちど復習しましょう。
集合とは、何かの物の集まりを表現するための概念で、そこに含まれる個々のものを要素とか元と呼びます。
例えば、果物の集合を考えた時
果物 = { りんご, メロン, いちご… }
のように表すことができます。
また、これをテーブルに置き換えれば果物がカラム名、りんご、メロン、いちごなどがカラムの値に該当するというわけです。
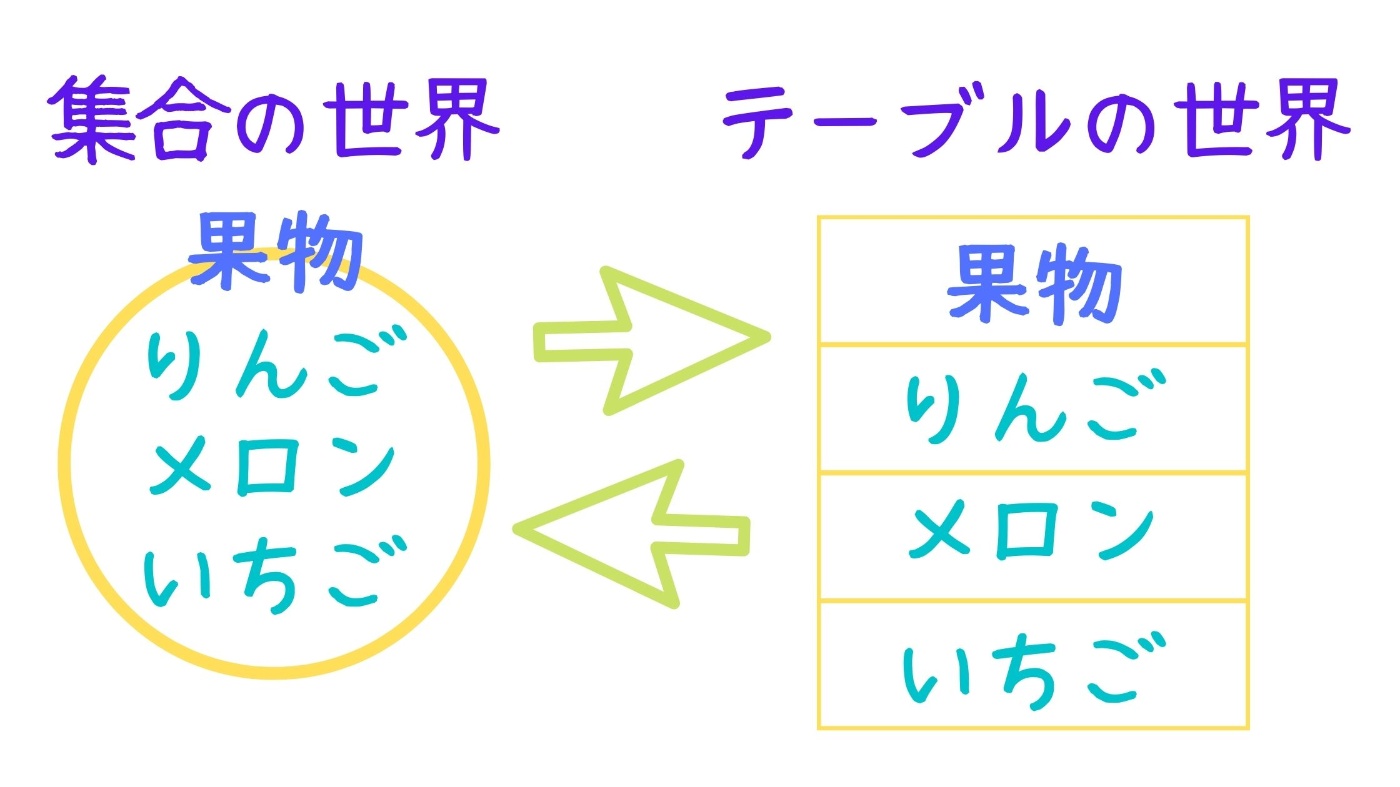
そして、個々の集合同士や要素同士は演算が可能なのでした。
これが、テーブル理論の背景となっている技術、すなわちリレーショナルモデルと呼ばれる技術です。
リレーショナルモデルとは、現実世界のデータを「リレーション」と呼ばれる概念を用いて表現するデータモデルで、テーブル自身のことをリレーションと呼んだりします。よくある間違いはテーブル同士の関係をリレーションと呼ぶことです。
さて、集合論の話に戻ります。
集合論において、要素もしくは元になるためにはある重要な2つの条件を満たす必要があります。
条件1
集合に含められる要素は、確実に存在しているものに限定する。
条件2
集合の要素は重複を許さない。
どういうことでしょうか?
さらにバックボーンを深掘りしていきましょう。
第2項 涼宮ハルヒと閉世界仮説
論理学において閉世界仮説とは、「現時点で真であると判明していないことは偽であると仮定する」理論のことです。逆を開世界仮説と呼び、現時点で真であると判明していないことであっても偽であるとはみなしません。
少しわかりにくいかと思うので、名作アニメ『涼宮ハルヒの憂鬱』を題材に閉世界仮説について考えてみます。「ただの人間には興味ありません この中に宇宙人 未来人 異世界人 超能力者が居たら私の所に来なさい 以上!」とは、主人公の涼宮ハルヒの名言です。
このような立場の逆が閉世界仮説の理論です。
すなわち「あるかわからないものはないものとする」という概念で、例えば、宇宙人や未来人、異世界人、超能力者はいるかわからないのでとりあえず存在しないものとして扱うという考え方です。
一方、涼宮ハルヒは開世界仮説の立場に立つので、宇宙人や未来人、異世界人、超能力者はいるかわからないのでとりあえず存在するものとして扱う、すなわち「あるかわからないものはあるものとする」という立場に立っています。
まとめると、閉世界仮説は論理学、あるいは我々が通常直感的に用いる論理で採用されている考え方で、お化けや幽霊、宇宙人など証明されていない、存在が示されていない現象や物体を、とりあえずないものとみなす、というものです。

話を集合の要素の条件のところに戻しますと、条件の1である「集合に含められる要素は、確実に存在しているものに限定する」という考え方は、すなわち、閉世界仮説であることを指します。
集合に含められる要素は、確実に存在しているものに限定する。
=集合に含められる要素は、閉世界仮説であるとする。
このような背景のもとで、最初のデータベース関連の基盤開発が行われていきました。
ところで、「あるかわからないものはないんだ!」という言い方をすると、いやいやそんな訳ないだろう、という感じがしますよね。実は、このことがコンピュータの融通の利かなさに繋がっているのではないかと疑われていました。
そこでリレーショナルDBの開発者たちは集合の要素の条件として、新たに「開世界仮説」の導入を検討します。開世界仮説では、「あるかわからないものはない」ということにはなりません。
(リレーショナルDBにおける)集合に含められる要素は、確実に存在しているものに限定しない。
=(リレーショナルDBにおける)集合に含められる要素は、開世界仮説であるとする。
この時導入された開世界仮説の存在をNullと呼びます。
ところがこの検討内容をリレーショナルDBに導入した結果判明したのは、開世界仮説を集合の要素として採用した場合、論理のプロセス自体がすぐに破綻してしまうし、そうでなくても「偽」のかわりに「わかりません」というだけのことになる、と。
これが正規化理論が必要になってしまった背景の1つ目です。
第3項 開世界仮説とNullという劇薬
通常、プログラムにおいて論理は「true」か「false」の2値で表されるもので、この考え方を2値論理と呼びます。
しかしながら、リレーショナルDBでは「true」と「false」とは別に「Null」と呼ばれる値が加わり、これを3値論理と呼ぶわけです。
このNullには以下の意味があります。
① 不明・未知(Unknown) であること
② 非存在・適用不能(Inapplicable) であること
①は、「値は存在するはずだが、どんな値かはわからない場合、とりあえずあることにする」という状態(開世界仮説)を指します。
②は「値が存在しない」ということを指します。
先述しましたが、DBの技術は元々数学的な集合論で採用されていた閉世界仮説に裏打ちされた技術であったのに、コンピュータの融通の利かなさはこのあたりが原因ではないのかと考えて開世界仮説のNullを生み出し、DBの世界に持ち込んだ結果、大変な混乱を起こしてしまったんですね。
このような背景もあり、Nullはbillion dollar mistake(10億ドル規模の損失をもたらす過ち) と呼ばれています。
第4項 多重集合の採用と重複の誕生
続いて条件の2にも焦点を当てていきます。
要素の重複を許す集合を、特別に多重集合と呼びます。
元々テーブルという考え方はデータを集めてまとめる、という目的のために作られた技術であったので集合ではなく多重集合の概念を基礎においています。
すなわち、実生活においてデータを集計した場合に、同じようなデータはたくさん取れるのでその度に重複分を除外して純粋な集合論に帰結させることは現実に反する、という考え方になります。
リレーショナルDBでも当然、多重集合の考え方が採用されました。
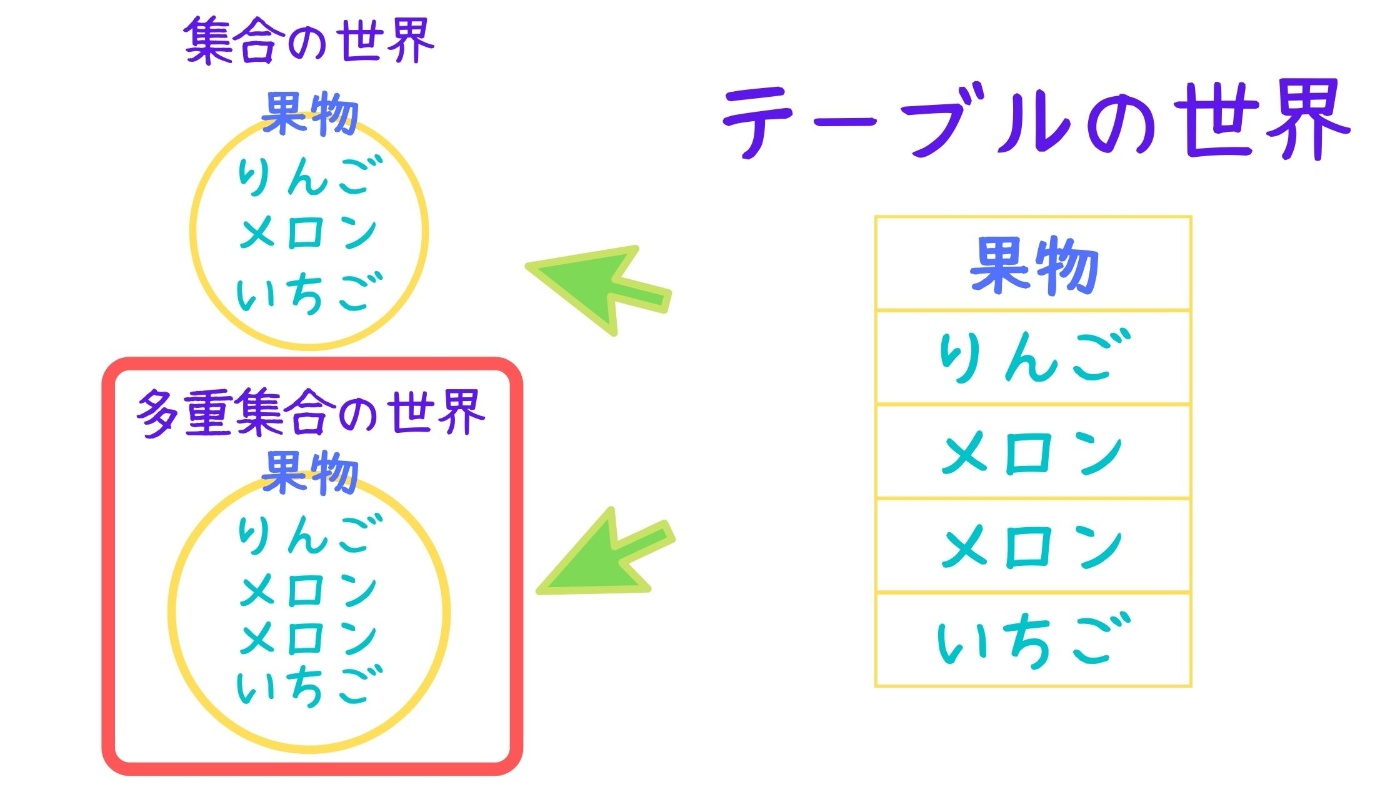
この結果、集合論の要素の条件2が修正されることとなります。
(リレーショナルDBにおける)集合の要素は重複を許すものとする。
第5項 正規化理論の登場
以上の背景より、元々の数学的な集合論には存在していなかったNullの採用(開世界仮説の採用)、また要素の重複許可(多重集合の採用)の結果、リレーショナルDBでは様々なエラーが発生するようになっていきました。
例えば、Null + 1の演算結果はどのような結果になるでしょうか。
答えはNullです。
あるかわからないものに1を足しても、「わからない」ことしかわかりませんね。
このように、SQLでNullになる可能性があるカラムを演算対象とする場合に、エラーが発生するようになります。select文やwhere文でカラムを指定した際に、どこかでNullが来ると式が崩壊することになるので、Nullだけ特別扱いしなきゃいけなくなるというわけです。
また、オプティマイザにも悪影響があります。クエリの実行が最適なパフォーマンスになるようチューニングしてくれるのがオプティマイザですが、Nullが出た瞬間、そのままでは計算が崩壊します。
こうして、我々はNullや重複という脅威に対して正規化理論と呼ばれる論理学の延長線上にある概念を生み出します。
この理論の究極目的は、Nullという開世界仮説の存在や重複を抹殺し、DBを再び純粋な集合論の世界に持ち込むことです。
そこで我々はテーブルの分割により、これを実現しようとします。
重複を排除した結果のテーブルには以下のような利益があると言われています。
- 異常を防げる
- 必要なデータがどこにあるかが明確になる
- クエリの記述が宣言的になる
- 不要な無損失分解が必要ない
- 複雑な制約が必要ない
- アプリケーションのコードに無駄がなくなる
- 性能が向上する
まとめますと、閉世界とは数学の理論に裏打ちされた綺麗な論理の世界であり、正規化とは、この世界に誕生してしまったNullと呼ばれる開世界の存在や重複を抹殺するための理論ということになります。
終わりに
データベースの正規化に関する具体的な手続きの方法は、検索すればたくさんヒットします。
ただし、その理論的なところは数学的な理論に基づくものであり、難解と感じる部分もあるかと思います。
今回はこの正規化理論の背景的なところを紹介することで、少しでも理解が助けれればと思い記事を投稿しました。
正規化の方法の解説などは別のネット記事などに譲りますので、豆知識程度に背景を知っておくと、より理解が深まるかと思います!
Discussion