🙄

【NTT（数論変換）入門（１）】DFT（離散フーリエ変換）編

2024/03/29に公開

Security

格子暗号の（高速化）の理解のためにはNTTが避けて通れない。何番煎じかと思われるかもしれないが、フーリエ変換系は多くの人が躓くポイントかと思うので（私も十分理解していないが）、わかりやすくまとめられると良いなと思う。

はじめに（全体像）

まずNTTとは何かを述べる。簡単に言うとNTTはDFTの一般化である。DFTは複素（関）数を複素（関）数へ写す全単射写像であり、要は複素数の表現方法を変換するエンコード処理だとみなしてよいと思う。全単射なので逆写像IDFTが存在し、これはエンコードした複素数を元に戻すデコード処理と考えることができる。

なぜこのような変換が重要なのかというと、変換後のほうが複素数に対する演算を楽に行うことができるからだ。暗号的にはモンゴメリ乗算みたいなものである。工学的には、時間領域より周波数領域が扱いやすいとかという言い方になるが、数論的には値を指数表現することで乗算を加算に変換するような例がわかりやすいかと思う。

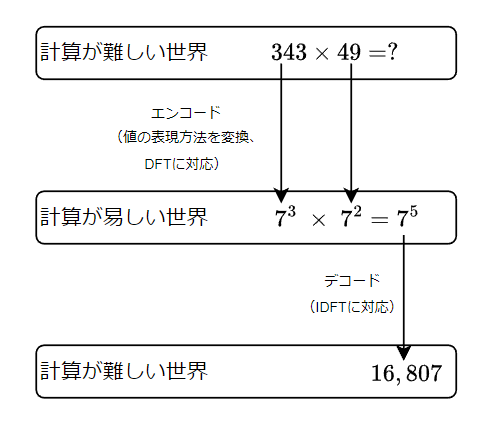
下の図の例で、我々は $343 \times 49$ を計算したいとする。しかしながらこの計算は暗算でやるにはちょっとめんどくさい。そこで値を計算しやすい空間に変換することを考える。どうやるかはひとまず置いておいて、 $343=7^3, 49=7^2$ のように表現方法を変換（エンコード）できる。指数表現では乗算は指数の加算に置き換わるため、 $7^3 \times 7^2 = 7^5$ は暗算で楽々計算できるだろう。これまたどうやるかはおいておいて、 $7^5$ という表現を $16,807$ に変換（元の空間へデコード）できれば、暗算でやるには少々面倒だった計算がらくらく計算できてうれしい。
気持ち的にはこの例のエンコードに対応するのがDFT (NTT)であり、デコードに対応するのがIDFT (INTT)である。（これはあくまでDFTの気持ちを伝えるための例であり、DFTによって値が指数表現に変換されるわけではない。）
ではDFTとNTTは何が違うんだという話になるが、DFTは複素数含む少数点数の変換が行えるのに対し、NTTは整数を整数へ変換する。こう書くとDFTがNTTの上位互換っぽくなるがそうではない。小数点数というのは厳密には無限の長さの値であり、PCでは値を正確に表現できないため、計算を繰り返していくうち誤差が蓄積して計算誤りが発生する可能性がある。それに対してNTTは整数を扱うため、（ある範囲の値までは）誤差なく計算することができるし、多くの暗号応用上も整数を扱得たほうが便利なことが多い。とはいえDFTとNTTは扱う値が異なるだけでやってることは同じである。そこで本稿ではまずDFTを解説する。

ちなみに、上の例では確かに乗算を加算に変換して易しく計算できるようになったように感じるが、これはエンコード/デコードの計算量を無視していることに注意。 $343=7^3$ や $7^5=16,807$ を求めるほうが元の問題より難しいじゃないかといわれると、全くその通りである。これはDFT/IDFTにも同じことが言えて、実はこいつらの計算がかなり難しくて、元の $343 \times 49$ より難しかったりする。すなわち

計算量（計算が難しい世界での乗算）< 計算量（エンコード+計算が易しい世界の乗算+デコード）

なのである。意味ないじゃないか。
しかしながらいくつかの工夫を取り入れるとDFT/IDFTの計算量を大きく削減することができ、このアルゴリズムはFFT（高速フーリエ変換）と呼ばれる。暗号の文脈でNTTというとFFTで高速化したNTTを指すことが多く、これによって

計算量（計算が難しい世界での乗算）> 計算量（エンコード+計算が易しい世界の乗算+デコード）

とすることができるため、多くの（格子）暗号でNTTが利用されるのである！

DFT

といわけでまずDFTを解説する。世の中にDFTの解説はごまんとあるが、英語版wikipediaの定義を（適当に訳して）引用する。

DFTは $N$ 個の複素数のシーケンス $\{\bold{x}_n\}:=x_0,x_1,...,x_{N-1}$ を、別の複素数シーケンス $\{\bold{X}_k\}:=X_0,X_1,...,X_{N-1}$ に変換するものであり

$X_k=\sum_{n=0}^{N-1}x_n \cdot e^{-i2\pi\frac{k}{N}n}$
で定義される。

これは $\{\bold{x}_n\}$ を $\{\bold{X}_k\}$ に変換するときの各要素の計算方法を示している。 $x_n$ と $e^{-i2\pi\frac{k}{N}n}$ をそれぞれ長さ $N$ のベクトルと見れば、 $\sum_{n=0}^{N-1}x_n \cdot e^{-i2\pi\frac{k}{N}n}$ はそれら二つのベクトルの内積計算に他ならない。 $e^{-i2\pi\frac{k}{N}n}$ が周波数 $k$ の正弦波（のベクトル表示）であることに着目すると、これは周波数 $k$ の正弦波に対する射影すなわち $\{\bold{x}_n\}$ に含まれている周波数 $k$ の正弦波成分の量となる。

逆変換であるIDFTも適当に引用しておこう

$x_n=\frac{1}{N}\sum_{k=0}^{N-1}X_k \cdot e^{i2\pi\frac{k}{N}n}$

やっていることはDFTと変わらないので特に説明することはない。 $e$ の符号が逆になっているところと、係数に $\frac{1}{N}$ がついているところがDFTとは異なる。 $\frac{1}{N}$ は正規化係数なので本質的にはDFT/IDFTどちらにつけても構わないし、両方に $\frac{1}{\sqrt{N}}$ をつけてもよい。
シーケンス $\{\bold{x}_n\}$ が時間波形、 $\{\bold{X}_k\}$ が周波数波形と考えるとこれは確かに時間領域から周波数領域の波形である。オイラーの公式的に周波数が何となく出てくるのは想像できる。
ただし時間とか周波数とかいうのは、工学応用上それが重要なだけであって、フーリエ変換の本質をとらえていない。実際NTTには時間とか周波数とか言った概念は出てこない。要は $e^{-i2\pi\frac{k}{N}n}$ が周波数を持つ三角関数であることはそんなに重要でないのである。DFT（およびNTT）の本質は、 $e^{-i2\pi\frac{k}{N}n}$ が回転という性質を持っていることにある。

回転子

e^{-i2\pi\frac{k}{N}n} \;\;\; (i)

の部分は、オイラーの公式

e^{ix}=\text{cos}x+i\text{sin}x

を使うと、複素平面上の単位円として幾何的に表すことができる。

k, n, N

は全てインデックスなので自然数であり、従って(i)式は、単位円を

N

等分したときの（マイナスがついているので逆方向に）

kn

番目の点であるとみなせる。

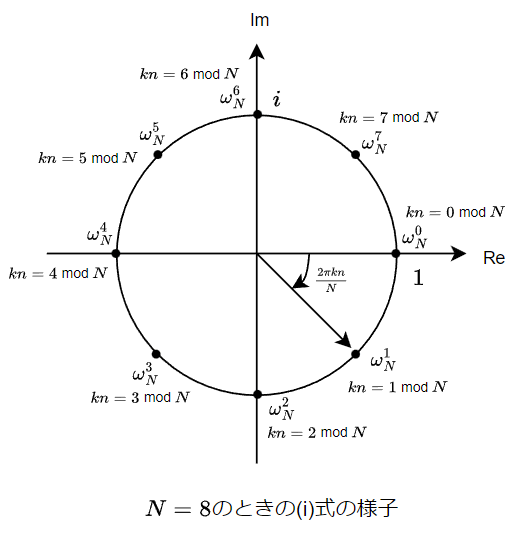
これは

kn=N

で1周する回転を表すものであるから、

kn

はmod

N

の世界で考える。

このように(i)式は単位円 $N$ 等分点のどれかを $kn$ によって示すものだった。そこで $\frac{-i2\pi}{N}$ を定数とみなし $e^{\frac{-i2\pi}{N}}=\omega_N$ と置くと(i)式 $=\omega_N^{kn}$ と書くことができ、ずいぶん見通しがよくなる。 $\omega_N$ を回転子と呼んだりする。

さて、 $\omega_N$ がフーリエ変換の本質といってよいほど重要なものであるが、図を見れば明らかなように $\omega_N^{kn}$ は複素平面の相違なる $N$ 個の値をとり、かつ $\omega_N^{N}$ の時に初めて $1$ となる数である。このような $N$ 乗して初めて1になる数は実は三角関数以外にも存在し、1の原始 $N$ 乗根と呼ぶ。フーリエ変換の性質の多くは1の原始 $N$ 乗根の性質に依存しており、1の原始 $N$ 乗根が存在する空間であればフーリエ変換を定義することができる。具体的には、複素数体から一般の環上へフーリエ変換を一般化できる。NTTは一般化DFTの一種であり、有限体上の1の原始 $N$ 乗根を使うものであるが、解説のためには複素平面が使えるとありがたいので、まずこのまま複素数体上のDFTで解説を進める。

1の原始 $N$ 乗根の性質

（複素数体上の）1の原始 $n$ 乗根 $=\omega_N$ には、次のような性質がある。

$\omega_N^{N}=1$
$\omega_N^{0},\omega_N^{1},\omega_N^{2},...\omega_N^{N-1}$ は全て相違なる。
$\sum_{n=0}^{N-1} \omega_N^{kn} = 0 \quad (1 \leq k < N) \qquad (ii)$

一番上は定義より自明、二つ目も上の複素平面の図を見れば、 $N$ 等分点がすべて異なる複素数となるのは明らか、問題は3つ目(ii)式である。
(ii)式は $k,n$ の2変数あるため見通しが悪いが、行列的に書くと次のような意味である。

\begin{bmatrix}0\\0\\\vdots\\0\end{bmatrix} = \begin{bmatrix} \omega_N^0&\omega_N^1&\omega_N^2&\cdots&\omega_N^{N-1} \\ \omega_N^0&\omega_N^2&\omega_N^4&\cdots&\omega_N^{2(N-1)}\\ \vdots&\vdots&\vdots&&\vdots\\ \omega_N^0&\omega_N^{n-1}&\omega_N^{2(n-1)}&\cdots&\omega_N^{(N-1)(N-1)}\\ \end{bmatrix} \begin{bmatrix}1\\1\\\vdots\\1\end{bmatrix}

この行列の $j$ 行目は、 $\omega_N^0=1$ から始めて、 $\omega_N^j$ 回転を繰り返したものの和が $0$ である、といっている。これに関しては、等比数列の和の公式を使った証明や代数的な証明がよく見られて、確かにそうなるのだがいまいち釈然としない。なので正確さをある程度犠牲にして幾何的に考えてみよう。

複素平面で見ると下図のようになる。この図は $N=6$ なので $\omega_N$ は-60度回転を表す。よって行列の1行目（ $n=1$ ）は-60度単位の回転をすべて足したものの和である。これは赤で示した位置ベクトルの和に等しく、あるベクトルに対してその逆向きのベクトルが存在することから和が0になることは容易にわかる。
2行目（ $n=2$ ）は-120度単位の回転 $\omega_N^2$ の和であり、3回で1周するが、和としては2周分とっている。しかしながら $\omega_N^2+\omega_N^4=\omega_N^3$ であり、これと $\omega_N^0$ が逆向きであるから、総和は0となる。

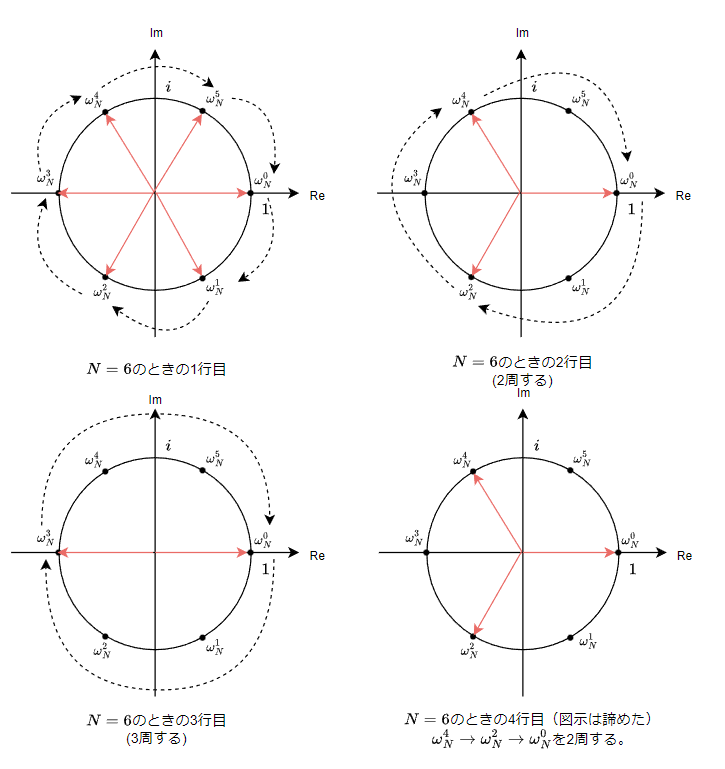
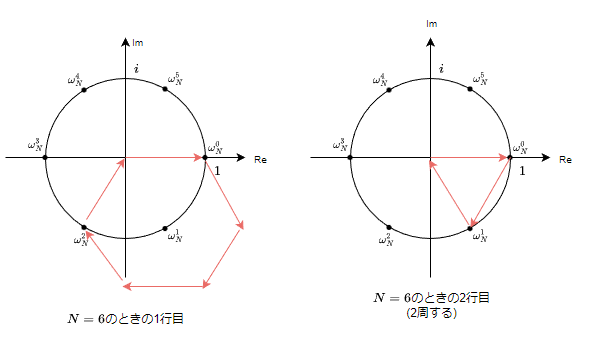
また、次のように考えることもできる。行列の1行目（ $n=1$ ）の和は、原点からスタートして距離1進み-60度回転を6回繰り返すものであるから、その軌跡（和）は正6角形となり原点（0ベクトル）に戻ってくるのである。2行目（ $n=2$ ）では-120度回転になるから正三角形になり、同じように原点へ戻ってくる。このように考えると(ii)式が成り立つことがわかるかと思う。

直交性

（複素数体上の）1の原始 $N$ 乗根の最も重要な性質が、直交性である。
(ii)式は実は直交性を表している。
(ii)式を $k=a-b$ として変形すると

\sum_{n=0}^{N-1} \omega_N^{(a-b)n} = \sum_{n=0}^{N-1} \omega_N^{an}\omega_N^{-bn} = 0 \quad (k \neq 0)

これは複素ベクトル(

\omega_N^{0}, \omega_N^{a}, \omega_N^{2a},...

)と(

\omega_N^{0}, \omega_N^{b}, \omega_N^{2b},...

)の内積に他ならない。
つまり、上に示した行列の相違なる2行の内積は0になる（すなわち直交しているのである）。

また、 $k=0$ すなわち $a=b$ の場合は明らかに

\sum_{n=0}^{N-1} \omega_N^{(a-b)n} = \sum_{n=0}^{N-1} 1 = N

であるから、これらをまとめて

\sum_{n=0}^{N-1} \omega_N^{(a-b)n} = \begin{cases} 0 &(a \neq b) \\ N &(a = b) \end{cases}

と表すことが多い。両辺を $1/N$ で正規化することで右辺をクロネッカーのデルタとし、規格直交系としてもいい。

DFTとIDFT

直交性がわかれば、DFTとIDFTがなぜ逆変換の関係にあるかを理解することができる。
DFTとIDFTの式をもう一度示す。

$X_k=\sum_{n=0}^{N-1}x_n \cdot \omega_N^{-kn} \qquad \text{(DFT)}$

$x_n=\frac{1}{N}\sum_{k=0}^{N-1}X_k \cdot \omega_N^{kn} \qquad \text{(IDFT)}$

IDFTの式へDFTの式を代入すると

\begin{align} x_{n'} &= \frac{1}{N}\sum_{k=0}^{N-1} (\sum_{n=0}^{N-1}x_n \cdot \omega_N^{-kn}) \cdot \omega_N^{kn'} \\ &= \frac{1}{N}\sum_{k=0}^{N-1}(\sum_{n=0}^{N-1} x_n \cdot \omega_N^{k(n'-n)}) \\ &= \frac{1}{N}\sum_{n=0}^{N-1}(\sum_{k=0}^{N-1} x_n \cdot \omega_N^{k(n'-n)}) \\ &= \frac{1}{N}\sum_{n=0}^{N-1} x_n \sum_{k=0}^{N-1} \omega_N^{k(n'-n)} \end{align}

直交性を利用すると $n=n'$ のときに $x_{n'}=x_{n}$ となり元に戻ることがわかる。

このようにDFT/IDFTによって、あるシーケンスを同じ長さの別のシーケンスに表現変更できることがわかった。ただこの段階ではDFT/IDFTともに $O(N^2)$ の計算量がかかる。多項式乗算の計算量も次数 $N$ に対して $O(N^2)$ であることを考えると、全然早くならないのであるが、FFTという素晴らしいアルゴリズムによって $O(N\text{log}N)$ に抑えられる。それはまたいつか・・・

次回

参考

ある程度厳密なDFT
https://mathlog.info/articles/2579

はじめに（全体像）

DFT

回転子

1の原始N乗根の性質

直交性

DFTとIDFT

次回

参考

Discussion

1の原始 $N$ 乗根の性質