📚

【NTT（数論変換）入門（２）】NTT（数論変換）編

2024/03/30に公開

前回の記事

数論変換

前回の記事では、複素数体上で定義されるDFTおよびIDFTについて解説した。DFTの本質は1の $N$ 乗根である $e^{\frac{-i2\pi}{N}}=\omega_N$ の直交性

\sum_{n=0}^{N-1} \omega_N^{(a-b)n} = \begin{cases} 0 &(a \neq b) \\ N &(a = b) \end{cases}

によるものであるため、この性質（1の主 $N$ 乗根とか主要根とかと呼ぶ）をもった数が存在する空間であればDFT (IDFT)を定義することができる。
1の主 $N$ 乗根存在の必要十分条件については私はよくわかっていないが、ひとまず体上の1の原始 $N$ 乗根であればよいようである（体ではない剰余環に存在することもある）。
すなわち任意の体上でDFT/IDFTを定義することができ、それこそが数論変換である。

$\mathbb{Z}/13\mathbb{Z}$ 上のNTT

1のN乗根と原始 $N$ 乗根

$\mathbb{Z}/13\mathbb{Z}=\mathbb{Z}_{13}$ は体であるから、NTTを定義可能である。まずこの体に、どんな1の（原始） $N$ 乗根が存在するのか考えてみよう。

正の整数 $\xi$ と位数 $p$ に対して、 $p=\xi N+1$ なら1の（原始） $N$ 乗根が存在することが知られている。これはつまり、 $a \in \mathbb{Z}_{13}\backslash \{0\}$ に対して $a^{13-1}=1$ であるから、12の因数である $\{1,2,3,4,6\}$ 乗根が存在するということである。すなわち任意の元 $a$ は1の12乗根であり、 $a^2$ は6乗根、 $a^3$ は4乗根、 $a^4$ は3乗根、 $a^6$ は2乗根となる。

$\mathbb{Z}_{13} \backslash \{0\}$ の任意の元が1の12乗根なのだから、1の12乗根は当然12個ある。このうち原始12乗根はいくつあるだろうか？
上で述べたように、1の12乗根の中には6, 4, 3, 2, 1乗根が含まれており、これらは原始12乗根ではない。例えば1は明らかに12乗根ではあるが原始12乗根ではない。つまり、12乗根から（原始）6, 4, 3, 2, 1乗根を差っ引いたものが原始12乗根になる。

このような考えに基づいて原始 $N$ 乗根だけを解に持つ方程式を構成することができ、これは円分多項式 $\Phi_{N}$ と呼ばれる。 $\Phi_{12}=x^4-x^2+1$ であるから原始12乗根は4個存在する（次数はオイラーのトーシェント関数で求められる）。

1の原始根と原始 $N$ 乗根

実は位数 $q$ の有限体 $\mathbb{F}_q$ に対する原始 $q-1$ 乗根には原始根という特別な名前がついている。これは原始 $q-1$ 乗根が $\mathbb{F}_q$ の乗法群を生成する生成元となるためである。
上で述べたように原始12乗根は4つ存在するから、 $\mathbb{Z}_{13}$ の原始根も4つ存在することになる。原始根の具体的な計算方法は私はよくわかっていないが（すべての元を試していけばそれなりに高い確率で見つかるはず？）、とりあえず $2,6,11,7$ の4つであることが天下り的にわかっている。

これらはそれぞれ、

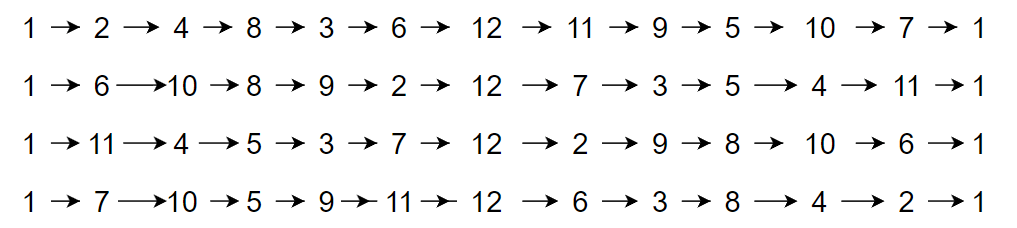
こんな感じで4つの巡回群を生成する。左端と右端がくっついて円になっているイメージを持ってほしい。

DFTの記事で紹介したように、 $N$ 乗根は単位円上を $N$ 等分する点であり、原始 $N$ 乗根は $\omega^0=1$ から初めて最初に来る点であった。つまり

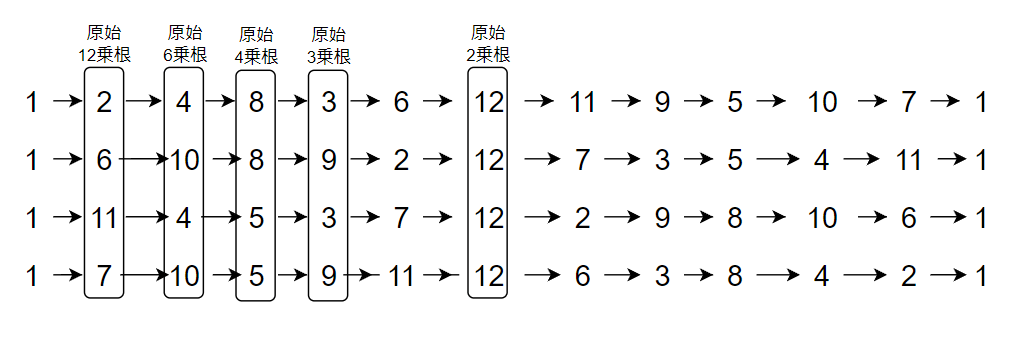
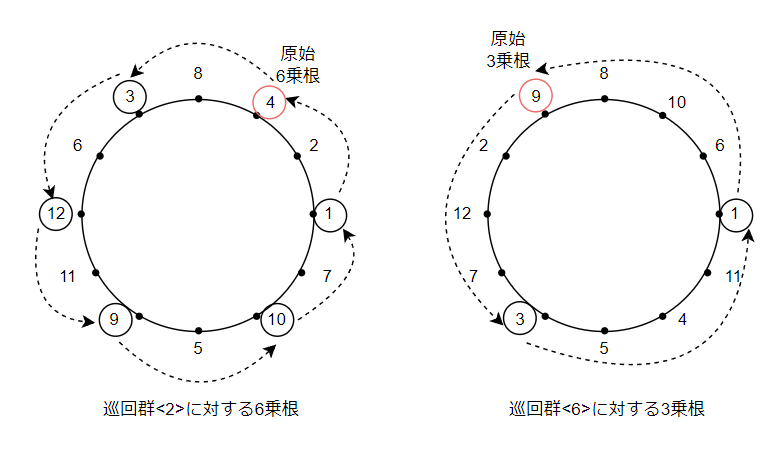
のように、有限体上でも単位円のような回転のイメージを持つことができ、DFTもNTTもほぼ同じであることがわかる。また1の原始12乗根は4つの巡回群で計4つ存在し、原始6乗根や3乗根は重複が存在するため2つしかないことがわかる。

1の原始 $N$ 乗根の直交性

DFT（NTT）に対してIDFT（INTT）を行うためには、1の原始 $N$ 乗根に直交性が必要なのであった。NTTでは複素数を使わないので、DFTのときのように複素平面上で位置ベクトルが0になるという直観的な説明をしていいのかわからない。代数的な証明についてはWikipediaの証明を引用しておくとして、 $\mathbb{Z}/13\mathbb{Z}$ の例でちゃんと直交していることを確認しておこう。

直交性とはつまり、行列

\begin{bmatrix} \omega_N^0&\omega_N^0&\omega_N^0&\cdots&\omega_N^{0} \\ \omega_N^0&\omega_N^1&\omega_N^2&\cdots&\omega_N^{N-1} \\ \omega_N^0&\omega_N^2&\omega_N^4&\cdots&\omega_N^{2(N-1)}\\ \vdots&\vdots&\vdots&&\vdots\\ \omega_N^0&\omega_N^{n-1}&\omega_N^{2(n-1)}&\cdots&\omega_N^{(N-1)(N-1)}\\ \end{bmatrix}

のすべての行ベクトルの組み合わせで内積が0になるということ（もしくは1行目以外の各行の要素の和が0になること）である。 $N=6$ として原始6乗根である4を持ってくると、

\begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 4 & 3 & 12 & 9 & 10 \\ 1 & 3 & 9 & 1 & 3 & 9 \\ 1 & 12 & 1 & 12 & 1 & 12 \\ 1 & 9 & 3 & 1 & 9 & 3 \\ 1 & 10 & 9 & 12 & 3 & 4 \end{bmatrix}

となり、1行目以外の行の要素の和が0になっていることはすぐにわかる。

素数べき体上のNTT

いつか書きたい

結局NTTとは何なのか

有限体上でやるDFTである。
NTTとその高速化（FFT）を一緒に解説するが多いため難しく感じるが、DFTとおなじ、というか整数を扱う分DFTよりも易しいくらいである。
浮動小数点数を使わないので、計算誤差がないという点でDFTより優れているともいえるが、この時点ではNTTはDFTと同じ計算量 $O(N^2)$ であるため、実用上はメリットが少ない。
次は、DFT（NTT）によってどのような演算がどのような演算に写されるのか、そして高速化手法について解説する。

次回予告

畳み込み定理　-> FFT

参考文献

NTTの条件について

https://mathlog.info/articles/2658

原始根について

1の $N$ 乗根の求め方

Discussion

ログインするとコメントできます