【耐量子計算機暗号・PQC】CRYSTALS Kyber実装してみる。鍵生成
NISTに提出されているkyberのspecificationを見て、kyberを実装してみよう。
格子暗号自体は難しいものではないが、
サンプリングやら圧縮やらのあたりがよくわかっていない。果たして正しく実装できるだろうか。specificationだけではわからないこともおおいので、リファレンス実装refをかなり参考にする。
CPAPKE.KeyGen
鍵生成アルゴリズムは以下。

パラメータについて以下にまとめる
| Kyber | |||||||
|---|---|---|---|---|---|---|---|
| 512 | 256 | 2 | 3329 | 3 | 2 | (10,4) | |
| 768 | 256 | 3 | 3329 | 2 | 2 | (10,4) | |
| 1024 | 256 | 4 | 3329 | 2 | 2 | (11,5) |
また共通鍵プリミティブについては、FIPS-202(つまりSHA-3ファミリ)で、次のように定義される(カッコ内は90sバリアント)
- XOF: SHAKE-128 (CTR mode AES-256)
- H: SHA3-256 (SHA-256)
- G: SHA3-512 (SHA-512)
- PRF(
s,b s||b - KDF: SHAKE-256 (SHA-256)
さて、アルゴリズムの1行目から順に見ていこう
乱数生成
1行目のrandombyte関数で乱数取得しており、これはrandombyte.cで定義されている。基本的にはSYS_getrandomなどのOSが提供するエントロピーソースを使うようになっている。しかしながらテストベクタを生成するには真正乱数は都合が悪く、test_vectorsプログラムの生成時にはtest_vectors.cで定義される疑似乱数版randombytesがリンクされる。
これはどうやらSUPERCOPの関数のようだが、何をやっているか正直わからない。シードをごちゃごちゃやって乱数っぽいものを作っているが、とりあえずこの部分はテストベクタで与えられるものをそのまま使って、実装範囲外とする。
例えばtest_vectors512で最初に出力される乱数は
である。
512-bitハッシュ
続いて2行目の
SHA3はライブラリがあると思われるのでそれを使えばいいと思うが、一度も実装したことがないので、一度作ってみるか・・・
hashlibを使ってこんな感じで実装
s = hashlib.sha3_512()
s.update(bytes.fromhex(hex(d)[2:]))
Gout = f'{s.hexdigest():0128}'
rho = int(Gout[:64], 16)
sigma = int(Gout[64:], 16)
行列A生成
4~8行目では
上で生成した乱数シード
Parse関数は、以下のような任意バイト列から(NTTドメイン)多項式を生成する関数であり、NTTドメインと通常ドメインは全単射なので、値をそのままNTTドメインとして使っても一様性は保たれるっぽい。
Parse関数は棄却サンプリングの一種?であり、ハッシュ関数で生成された一様分布と信じられる乱数列から、条件を満たすもの(

さて、よくわからないのはParseの入力となっている
とりあえずソースコードを追ってみると、単純にメッセージ
SHAKE-128はレート
というわけで適当に実装してみたのが以下。parse(xof())を行っているのはRqクラスのsample_uniform関数。hashlibのshake関数を使っているが、squeezeのやり方がよくわからなかったので672バイト(squeeze4回分)を出力して使っている。
import hashlib
n = 256
k = 2
q = 3329
eta1 = 3
eta2 = 2
du = 10
dv = 4
class Rq:
def __init__(self):
self.coeff = [0 for x in range(n)]
def __repr__(self):
return str(list(map(hex, self.coeff)))
@classmethod
def uniform_sample(cls, rho, j, i):
a = cls()
s = hashlib.shake_128()
s.update(bytes.fromhex(hex(rho*256*256 + j * 256 + i)[2:]))
xof_out = bytes.fromhex(s.hexdigest(672))
sample_cnt = 0
for i in range(0, 672, 3):
val = xof_out[i:i+3]
d1 = val[0] + 256 * (val[1] & 0xf)
d2 = (val[1] >> 4) + 16 * val[2]
if(d1 < q and sample_cnt < n):
a.coeff[sample_cnt] = d1
sample_cnt += 1
if(d2 < q and sample_cnt < n):
a.coeff[sample_cnt] = d2
sample_cnt += 1
return a
class MyKyber:
def __init__(self):
pass
def genA(self, rho):
A = []
for i in range(k):
for j in range(k):
A.append(Rq.uniform_sample(rho, j, i))
return A
秘密ベクトル\bold{s}
9~12行目では、
2項分布サンプリングのアルゴリズムは以下

2項分布000, 111しかないので確率0.125, 1が1 or 2個となるのはそれぞれ3回あるので確率0.375で生起する分布である。

PRFで出力した値の各ビットは一様分布で独立に生起したものと考えると、ここから
アルゴリズム中で、
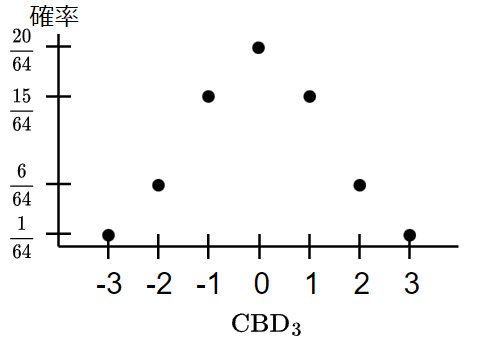
さて、
続いて、リファレンス実装の2項分布サンプリングがどうなっているか見てみる。
static void cbd3(poly *r, const uint8_t buf[3*KYBER_N/4])
{
unsigned int i,j;
uint32_t t,d;
int16_t a,b;
for(i=0;i<KYBER_N/4;i++) {
t = load24_littleendian(buf+3*i);
d = t & 0x00249249;
d += (t>>1) & 0x00249249;
d += (t>>2) & 0x00249249;
for(j=0;j<4;j++) {
a = (d >> (6*j+0)) & 0x7;
b = (d >> (6*j+3)) & 0x7;
r->coeffs[4*i+j] = a - b;
}
}
}
ここはいくつか実装依存部分があるように見える。まず、PRFの出力を24ビットごとにリトルエンディアンで取得し、4係数ずつサンプリングを行っている。d計算部分で0x00249249というマジックナンバーが使われているが、これはビットに直すと0b00000000001001001001001001001001となり、要は24ビットで3ビットごとに1が立っている値である。これをマスクとしてtをシフトしながら和をとることで、dは3ビットごとに2項分布からサンプリングした値が8個並ぶ形になる。内側のfor文ではa, bとして取り出し、a-bを各係数として採用している。a-bをすると当然負の値が出てくるが、ref実装では(仕様上では?)基本的に
2項分布サンプリングは他にも実装方法があると思うが、(32-bitアーキテクチャでは?)このやり方が効率がいいということなんだろう。
次のようにref実装をほぼそのまま実装
def sample_cbd(cls, sigma, nonce, eta):
poly = cls()
s = hashlib.shake_256()
s.update(bytes.fromhex(hex(sigma*256 + nonce)[2:]))
prf_out = bytes.fromhex(s.hexdigest(192))
for i in range(64):
t = int.from_bytes(prf_out[i*3:i*3+3], 'little')
d = t & 0x00249249;
d += (t>>1) & 0x00249249
d += (t>>2) & 0x00249249
for j in range(4):
a = (d >> (6*j)) & 0x07
b = (d >> (6*j + 3)) & 0x07
poly.coeff[4*i + j] = a - b
#負数を利用
return poly
エラーベクトル\bold{e}
13~16行目ではエラーベクトル
数論変換
19行目では
高速化手法の一つであるからやらなくても動かせるのであるが、specificationに組み込まれているので実装は必須である。数論変換については別記事で解説する。
難しいことをやってそうだが、計算自体は非常に単純でspecificationの式(4),(5)を参照すればよい。これは高速化してないバージョンなので

以下のように実装した。剰余乗算は単に%使ってる。一応FFTを使った高速化バージョンもref実装を参考に作ってみた(コメントアウトしてある部分)。
@classmethod
def ntt(cls, poly_in):
# Straight forward version
poly_out = cls()
for i in range(128):
for j in range(128):
zeta = zetas[(2*tree[i]+1)*j % n]
poly_out.coeff[2*i] += poly_in.coeff[2*j] * zeta
poly_out.coeff[2*i+1] += poly_in.coeff[2*j+1] * zeta
# # FFT version
# poly_out = copy.deepcopy(poly_in)
# kk = 1
# for len in [128, 64, 32, 16, 8, 4, 2]:
# for start in range(0, 256, 2*len):
# zeta = 17**tree[kk]
# kk += 1
# for j in range(start, start + len):
# t = zeta * poly_out.coeff[j + len]
# poly_out.coeff[j + len] = poly_out.coeff[j] - t
# poly_out.coeff[j] = poly_out.coeff[j] + t
# Reduction
for i in range(n):
poly_out.coeff[i] %= q
#上の%qで値が正になるので、ref実装に合わせるため[-q/2,q/2]の範囲に戻す。
if poly_out.coeff[i] > 1664:
poly_out.coeff[i] -= q
#bit_reverse = int(f'{i:08b}'[::-1], 2)
return poly_out
アフィン変換
19行目の
ここでの演算は行列
リファレンスコードの該当箇所は、こんな感じ。
// matrix-vector multiplication
for(i=0;i<KYBER_K;i++) {
polyvec_basemul_acc_montgomery(&pkpv.vec[i], &a[i], &skpv);
poly_tomont(&pkpv.vec[i]);
}
polyvec_add(&pkpv, &pkpv, &e);
polyvec_reduce(&pkpv);
polyvec_basemul_acc_montgomeryで内積を計算している。剰余乗算にはモンゴメリ乗算を使っているが、入力となる値のドメインが両方モンゴメリドメインにないため、剰余乗算後はpoly_tomontで
エラーベクトル加算後のリダクションpolyvec_reduceはBarrettリダクションだった。
以下のように実装した。多項式クラスRqに+,@オペレータをオーバーロードしている。
# Matrix-vector multiplication
As = [Rq() for x in range(k)]
for i in range(k):
for j in range(k):
As[i] = As[i] + (A[i][j] @ ntt_s[j])
class Rq:
...
...
def __add__(self, other):
tmp = self.__class__()
for i in range(n):
tmp.coeff[i] = (self.coeff[i] + other.coeff[i]) % q
#上の%qで値が正になるので、ref実装に合わせるため[-q/2,q/2]の範囲に戻す。
if tmp.coeff[i] > 1664:
tmp.coeff[i] -= q
return tmp
def __matmul__(self, other: Rq) -> Rq:
tmp = self.__class__()
for i in range(0, n, 2):
tmp.coeff[i] = self.coeff[i+1] * other.coeff[i+1]
tmp.coeff[i] = tmp.coeff[i] * 17**(2*tree[i//2] + 1)
tmp.coeff[i] += self.coeff[i] * other.coeff[i]
tmp.coeff[i] = tmp.coeff[i] % q
tmp.coeff[i+1] = self.coeff[i] * other.coeff[i+1]
tmp.coeff[i+1] += self.coeff[i+1] * other.coeff[i]
return tmp
エンコード
20, 21行目で計算した値を公開鍵

エンコードはデコードの逆変換として定義されているため詳しくは説明されていないが、単純に12ビットならでればいいのだが、リトルエンディアン的なのに注意
ref実装の該当箇所は以下
void poly_tobytes(uint8_t r[KYBER_POLYBYTES], const poly *a)
{
unsigned int i;
uint16_t t0, t1;
for(i=0;i<KYBER_N/2;i++) {
// map to positive standard representatives
t0 = a->coeffs[2*i];
t0 += ((int16_t)t0 >> 15) & KYBER_Q;
t1 = a->coeffs[2*i+1];
t1 += ((int16_t)t1 >> 15) & KYBER_Q;
r[3*i+0] = (t0 >> 0);
r[3*i+1] = (t0 >> 8) | (t1 << 4);
r[3*i+2] = (t1 >> 4);
}
}
2項(24ビット)ずつ3バイトに割り当てていっている。
まず負数に

エンコードなのでバイト列にすべきだが、整数値になるように実装した。
def encode(self) -> int:
val = 0
for i in range(0, n, 2):
elem0 = self.coeff[i]
elem1 = self.coeff[i+1]
if elem0 < 0:
elem0 += q
if elem1 < 0:
elem1 += q
val <<= 8
val += elem0 & 0xff
val <<= 8
val += ((elem1 & 0xf) << 4) | (elem0 >> 8)
val <<= 8
val += elem1 >> 4
return val
これで(ほぼ)完成!
CCAKEM.KeyGen
実はまだ完成じゃない。
上で作ったのはCPA安全版なので、FO変換してCCA安全に変換する必要がある。

秘密鍵に乱数と公開鍵のハッシュを含めるだけなので特に説明はない。
実装してみた
pythonで実装してみた。クラスなど適当に作っているので使いにくいと思うが、誰かの参考になればと思い晒し上げる。
テストベクタはref実装で生成している。
Discussion