Zenn
🔥

【耐量子計算機暗号・PQC】CRYSTALS Kyber実装してみる。暗号化/復号

2024/08/22に公開
Security
Security
耐量子計算機暗号
TLS
pqc
tech

暗号化

CPAPKE.Enc

Kyberの暗号化アルゴリズムは以下

大部分（4~20行目とか）は鍵生成の記事の説明と同じなのでそちらを参照のこと。
Kyber-512の場合\eta_1 \neq \eta_2であるのでe_2のCBDが若干異なることに注意

デコード

バイトアレイの3バイトずつを12ビットの多項式係数二つにする
公開鍵は255次多項式k個＋32バイト

ML_KEMの仕様書でもうちょっとちゃんと定義された。

バイトアレイをdビット整数の配列（多項式）にデコードする。dの範囲は1以上12以下
入力として32\times dバイトのバイトアレイBをとり、256要素の整数配列（255次多項式）F \in \mathbb{Z}_m^{256}を出力する。d<12のときは整数の範囲として最大となる2^dビット分使い、d=12のときは法qを最大値とする。

Compress and decompress

LWE系の暗号の復号は、ノイズを含む平文から丸め処理を行ってノイズを除去する必要がある。丸めは簡単にいうと下位ビットの情報を捨てることであり、復号には下位ビットの細かい情報は必要ない。よって暗号文の時点で下位ビットを捨てておくことで暗号文を短くしてしまえというのがCompressである。

以下はML-KEMのCompress/Decompressの説明部分。compressはx \in \mathbb{Z}_qをqで割ることでx \in \{0, \frac{1}{q}, \frac{2}{9},...,\frac{q-1}{q}\}の小数点数に直し、それをdビットシフトした時の整数部分と見ることができる。除算操作は重いのでやりたくないし、小数点数誤差も出したくないので同実装するかがポイントとなる。

ref実装のd=10のcompress処理は以下。4係数ごとに処理しているが、これはcompressとencodeを一緒にやっているからだと思われる。出力配列rはバイト列であり、4係数\times 10 bitsで40bitsが5バイト分に相当する。この辺のencode処理が最後のrに代入している部分である。

t[k] += ((int16_t)t[k] >> 15) & KYBER_Q;はunsigned化処理で、符号が立っている場合にqを足して値を正の範囲に補正している。

まずd0 <<= 10;することで小数点位置が10ビット目に移ったとみることができる。これに1665=q/2を足しているので、q/2^{11}を小数点誤差なく足すことに等しい。ここで繰上りが発生すれば天井に、しなければ床に丸められる。
最後にqで割る（1/q \risingdotseq 1290167/2^{32}を掛ける）ことをしている。

polyvec.c
void polyvec_compress(uint8_t r[KYBER_POLYVECCOMPRESSEDBYTES], const polyvec *a)
{
  unsigned int i,j,k;
  uint64_t d0;

  uint16_t t[4];
  for(i=0;i<KYBER_K;i++) {
    for(j=0;j<KYBER_N/4;j++) {
      for(k=0;k<4;k++) {
        t[k]  = a->vec[i].coeffs[4*j+k];
        t[k] += ((int16_t)t[k] >> 15) & KYBER_Q;
/*      t[k]  = ((((uint32_t)t[k] << 10) + KYBER_Q/2)/ KYBER_Q) & 0x3ff; */
        d0 = t[k];
        d0 <<= 10;
        d0 += 1665;
        d0 *= 1290167;
        d0 >>= 32;
        t[k] = d0 & 0x3ff;
      }

      r[0] = (t[0] >> 0);
      r[1] = (t[0] >> 8) | (t[1] << 2);
      r[2] = (t[1] >> 6) | (t[2] << 4);
      r[3] = (t[2] >> 4) | (t[3] << 6);
      r[4] = (t[3] >> 2);
      r += 5;
    }
  }
}

メッセージデコード

20行目で32バイトメッセージを多項式にデコードしている。32バイトから256係数つくるために、メッセージの1bitを1係数にしている。Decodeで{0,1}係数の多項式にした後、Decompressで\mathbb{Z_q}範囲（{0,1665}）にする。

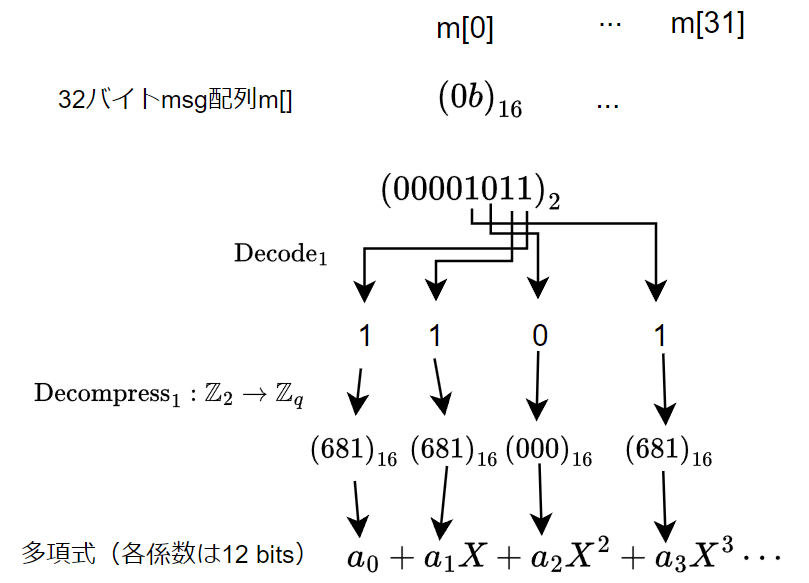
ref実装のコードはこんな感じ。下手に{0,1665}のテーブルを作るよりmaskでANDしたほうが早いのだろう。

poly.c
void poly_frommsg(poly *r, const uint8_t msg[KYBER_INDCPA_MSGBYTES])
{
  unsigned int i,j;
  int16_t mask;

#if (KYBER_INDCPA_MSGBYTES != KYBER_N/8)
#error "KYBER_INDCPA_MSGBYTES must be equal to KYBER_N/8 bytes!"
#endif

  for(i=0;i<KYBER_N/8;i++) {
    for(j=0;j<8;j++) {
      mask = -(int16_t)((msg[i] >> j)&1);
      r->coeffs[8*i+j] = mask & ((KYBER_Q+1)/2);
    }
  }
}

CCAKEM.Enc

CCA2安全にするため、CPAPKE.Encを以下のように利用する。
いわゆる決定的ナンス？rは公開鍵とメッセージのハッシュ値となっている。共有鍵Kのシード\bar{K}も同様に決定的に求められる（m自体が乱数ではあるが）。
共有鍵KはKDFで出力されており、KDFとしてXOFのSHAKE-128が使われているため、Kは任意の長さをとれる。

復号

CPAPKE.Dec

今まで説明してきた操作を使っているだけなので説明はほぼ割愛。

Decompress

Compressの逆操作であり、11ビット以下に圧縮された係数から12ビットを復元する。

ref実装のコード（d=10）はこんな感じ。
バイト列から多項式を復元するデコード操作とdecompressが同時に行われている。

void polyvec_decompress(polyvec *r, const uint8_t a[KYBER_POLYVECCOMPRESSEDBYTES])
{
  unsigned int i,j,k;
  uint16_t t[4];
  for(i=0;i<KYBER_K;i++) {
    for(j=0;j<KYBER_N/4;j++) {
      t[0] = (a[0] >> 0) | ((uint16_t)a[1] << 8);
      t[1] = (a[1] >> 2) | ((uint16_t)a[2] << 6);
      t[2] = (a[2] >> 4) | ((uint16_t)a[3] << 4);
      t[3] = (a[3] >> 6) | ((uint16_t)a[4] << 2);
      a += 5;

      for(k=0;k<4;k++)
        r->vec[i].coeffs[4*j+k] = ((uint32_t)(t[k] & 0x3FF)*KYBER_Q + 512) >> 10;
    }
  }
}

CCAKEM.Dec

いわゆるFO変換（の亜種？）で、入力暗号文cの正当性検証を行っている。
ML-KEMではこの部分がちょっと変更されたっぽい。

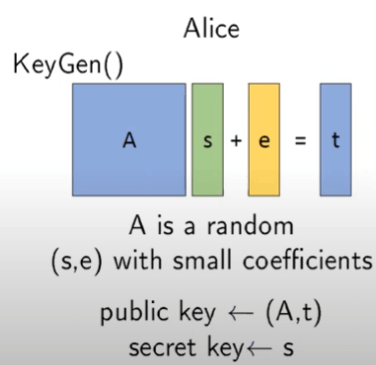
結局何をやっている？

Youtubeの説明より引用

KeyGen

Enc

Dec

v=r \cdot t + e_2 + m
u=r \cdot A + e_1
t=A \cdot s + e

であるから、復号v-u \cdot sは、

v- u \cdot s = r \cdot (A \cdot s + e) + e_2 + m - (r \cdot A + e_1) \cdot s \\ =r \cdot A \cdot s + r \cdot e + e_2 + m - r \cdot A \cdot s - e_1 \cdot s \\ = r \cdot e + e_2 - e_1 \cdot s + m

Github

Pythonで実装したもの。やっつけで作っているので型とかすごい適当

https://github.com/ankoman/kyber/blob/master/my_kyber/test.py

Discussion