多変量時系列予測の新展開📈 iTransfomer までの歴史まとめ

概要

先日国際会議に参加していたときに, 船の軌跡予測手法に関する発表で, iTransformerという手法を知った. ネットで調べると, すでに日本語記事がでている. だが, iTransformerはなぜ生まれる必要があったのか...従来手法の課題まで踏み込んだ記事は希少である.

そこで本記事では, これまでの時系列モデル系との比較を踏まえつつ, どのようなテクニックであるのかを体系的にまとめたい という記事である.

忙しい人向け

モデルタイプ	特徴	強み	課題
ARモデル / 状態空間モデル	過去の値の線形結合や統計的推定に基づくモデル（AR, ARIMA, Kalmanフィルタなど）	解釈しやすく理論的根拠が明確. 少データでも安定	非線形・長期依存や複雑な相互変数関係への対応が弱い
RNN / LSTM	時系列に沿った逐次学習型ニューラルモデル	非線形・長期依存の学習が可能. 柔軟性が高い	長期系列では勾配消失・爆発、並列処理が困難
従来のTransformer系	Self-Attention による全時点グローバル依存関係の利用	並列処理が得意で, 長期依存の捕捉に優れる	ルックバックが長くなると計算量爆発。時系列特有の構造（順序・変数）への対応が難しい
iTransformer	時系列 → 変量をトークンとする転換的構造	多変量相関の表現力, 並列処理, 高い汎化力, 計算効率の向上	新手法ゆえ汎用性や他タスクへの適応性など追加検証の余地あり
Minusformer	加法的集約を減法に変更	長期時系列の学習における, 学習誤差の蓄積を回避し, 重要な差分だけに集中させるようにしたiTransformerの拡張モデル

多変量時系列解析

ここのモデルを紹介するまえに, それらのモデルが扱う多変量時系列について説明する.
まず, (単変量)時系列とは, 時間方向に取得された数値データである. 例えば, 株価データなどはイメージしやすいでだろう.
そして, 時系列が多変量であるとは, 複数種類の時系列を集めたデータである. 例えば, 船のセンシングデータでは, 方向角速度(yaw rate), 横揺れ（rolling), 縦揺れ(pitching)および舵角（rudder angle) などが取得される. これを,同じ時間軸, スパンで並べたデータが多変量時系列である. ^[1]

多変量時系列を解析する場合, 各時系列間の影響関係, つまりは相関関係をも考慮することができる. 例えば,船のセンシングデータであれば, 方向角速度(yaw rate), 横揺れ（rolling)のデータ変動の関係性を解析できる.

こうした特徴を用いると, 多変量時系列では以下のメリットを受けられる

メリット	説明
予測精度の向上	一変量だけの場合より, 多変量時系列を用いてその一変量時系列の予測をした方が精度があがる
時系列の欠損に強い	多変量時系列を用いることで, ある時系列にてデータ欠損があった場合でもロバストに予測できる
制御の観点で有利	ある時系列を制御できるか, できないかに分けたとき, 制御できるほうの時系列を用いて, 他方の制御できない時系列のコントロールを間接的にできる可能性がある

時系列モデル

統計モデル系統

AR (Auto Regression) や, SARIMA(Seasonal ARIMA)などの古典的なモデル.
時系列解析といえばまずは出てくる代表的な統計的な解析手法である.

また, 多変量時系列をなんらかの制御系（システム）とみなすと, カルマンフィルターなどの状態空間モデルも使用できる.

ここら辺の話は, 過去に記事を出しているのでそちらを参考していただきたい.
https://zenn.dev/akitek/articles/0435176da6c849

統計系統の時系列モデルは, その理論的根拠が適切に整理・検証されているため, 解釈性が高い.
他方, ARモデルやカルマンフィルターなど, その多くが変数間, 時系列間の関係性を線形的なものとして扱っているため, 非線形・長期依存や複雑な相互変数関係への対応が弱いとされている.

RNN系統

そうした背景から, より複雑な関係性を把握できる深層学習(NN）的な手法が開発されていくとなった.
深層学習を時間方向に関するデータに利用する研究は(比較的）長い歴史をもつ. 例えば, 自然言語分野では, 過去の文字列から次の一単語を予測するという有名なタスクがあり, そこにRNN (recurrent Neural Network)と呼ばれる手法 が使われた.

この手法は, 入力（変数）と出力（ラベル）を紐づけるシンプルなニューラルネットワークを, 入力変数に時間方向・時間的順序を明示的に与えたモデルに拡張したものとみなせる.

このRNNは, 時系列データを扱えるようにした深層学習手法として有名であるが, 長期的な予測は苦手という課題があった. 自然言語の場合, かなり前に出た単語や文章が, 次の一単語を予測する上で重要な場合がある. そうした長いコンテキストの解釈にはRNNは弱い.

そこで出てきたのが, LSTM (Long short Term Memory)　と呼ばれるRNNの特別な一種である. 長期的な依存関係を学習することのできるのが特徴である.

LSTMは長期の依存性の問題を回避するように明示的に設計されている. (以下は記事より引用）
その構造から, 各ブロック（緑）にちょっとした記憶機能（パラメータ）があるのが特徴である.
これが, 通常のRNNに出てくる勾配消失の問題を改善している.

RNN/LSTMの詳細な説明は以下の記事で補ってほしい.
http://colah.github.io/posts/2015-08-Understanding-LSTMs/
https://qiita.com/KojiOhki/items/89cd7b69a8a6239d67ca#結論

英語記事の日本語訳版記事

さて, LSTMはほとんどのRNNの成果を上回り, 強力なツールとみなされてきた.
しかし, いまやTransformer時代となっている. それはなぜか?
その大きな理由として, スケーラビリティにおいてTransformerがとても強力であるからだ.
より大規模にデータを集めて学習したい場合, 時間がかかる計算を早くすることや, 使った分だけの精度向上を期待したいが, LSTMにはそこらへんが弱い.

以下, LSTMとTransformerの比較記事をまとめた表をあげておく.
https://www.kolena.com/guides/transformer-vs-lstm-4-key-differences-and-how-to-choose/

特徴 / 項目	LSTM（長短期記憶モデル）	Transformer（トランスフォーマー）
処理方式	順次処理（シーケンシャル）：各ステップが前の出力に依存 ([Kolena][1])	並列処理：全シーケンスを一度に処理可能
効率性・スケーラビリティ	スケールしにくく、大規模データ／長系列では計算時間が急増	並列処理によりトレーニングが高速で、大規模展開に向く
長期依存関係の扱い	ゲート構造により長期依存を比較的よく保持	Attention により遠距離の依存も直接的に捉えやすいが、コンテキスト長制限あり
適用に向くタスク	時系列・音声認識・コンテクスト重視の逐次タスクなどに強い	機械翻訳・長文要約・大規模言語タスクなどに主に使われる

選び方の指針（How to Choose?）

記事では、選択の際に以下の要素を考慮すべきとされています：

• データの性質：「逐次性」や「文脈・順序が重要」な場合は LSTM が適する. 対して「並列処理の効率」や「大規模データ処理」が重視される場合は Transformer が有力
• 計算資源：Transformer は GPU／TPU 等の高速並列計算環境で真価を発揮. LSTM はリソース制約下でも利用しやすい
• タスク要件：テキスト生成や文脈理解のような長い依存関係を要する場合は Transformer, 時系列予測や音声など逐次的な文脈保持が重要な場合は LSTM を検討
• スケーラビリティ：将来的に大規模化を見込むなら Transformer が適応しやすい. LSTM は大規模データや長系列では計算負荷が課題
• ハイブリッド構成：記事では、両者の長所を掛け合わせたハイブリッドアプローチも有効な選択肢として紹介

Transformer族

さて, RNN系統では大規模な学習ができない, ということからまた新たなモデルが開発されることとなる. それは, RNNを一切使わずにAttentionだけを使うことで, 入力と出力の文章同士の広範囲な依存関係を捉えられるモデル, みなさんご存知 Transformer(Vaswani et al., 2017)である.

自然言語処理のために作られたTransformerであったが,その後画像タスクへ拡張したVision Transformer(Dosovitskiy et al., 2021)をはじめ,さまざまなタスクへの拡張がされている.
時系列への適用もされているが, どのようにされているのか説明するために, まずはシンプルなTransformerのブロック図を確認する.(以下、論文より)

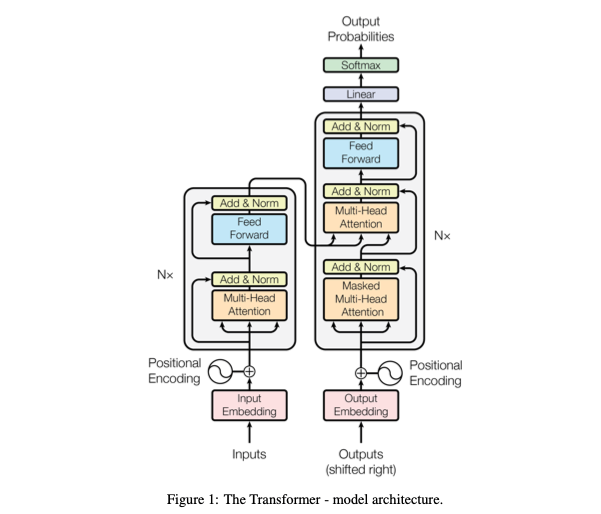
Transformerのブロック図には, RNNのような一単語と次の単語を逐次的に投入するような処理ではなく,文章の単語をまるごと入力し,処理している点が特徴である. ^[2]

このとき, RNNでは文字列の並びを入力に反映しているように, 代わりにTransformerではPositional Embeddingといった位置トークンを入力データに加えることで, 単語の文脈内での位置関係を考慮している.

Transformerの詳細な説明は以下の記事にお任せする
https://qiita.com/omiita/items/07e69aef6c156d23c538

さて, この位置トークンを工夫すれば時系列予測にも応用できるのでは？ というシンプルな疑問がでてくる. 例えば, 各時間帯で取得された数値データに, 取得時間（時間トークン; temporal Token)を加えてあげれば, 文章の単語予測同様, 過去の数値データから先を予測する時系列予測に応用できると考えられる.

例として, 気温予測モデルにTransformerを適用した研究もされている.

うまくいけていそうなTransformerベースの時系列モデルであるが, 実はこのトークンの付け方が重要であることがわかっており, 特にiTransformer以前のモデルでは時系列予測にうまく適用できていないと課題がでてきている. それを克服しようとしたのが本記事のメインテーマである, iTransformerである.

シンプルなモデルの方が強力？？

Transformer系統の時系列モデルが実は古典的な手法よりも弱いのではないか？という課題提起をした論文がある. タイトル通り, "Are Transformers Effective for Time Series Forecasting"Zeng et al., 2022と課題である.

以下にあげるのが, 論文のなかで言われているTransformer系統の課題である.

1. 時系列の順序性を捉えづらい
   • Transformer の自己注意機構は順序に不変（permutation-invariant）な性質をもっており, トークンの順番そのものが重要な時系列データに対して, 時系列の「順序情報」が失われやすいという問題がある.
   • これは, 位置エンコーディングを用いても完全には解消されない
   • 自然言語タスクでは, 厳密な単語の位置はさほど問題にならないため, 位置エンコーディングでも問題がない
2. 単純な線形モデルに劣る予測性能
   • 著者らは, 非常にシンプルな LTSF-Linear（一次線形モデル＋トレンド成分分解＋非自己回帰方式）を導入し, 9種類の実データセットにおいて既存のTransformer系モデルをすべて大きく上回るという結果を示した. 場合によっては 20〜50% の性能向上も報告
3. 長期入力（look-back window）の拡大でも改善せず
   • 通常, 長期の履歴情報の取り込み(ウィンドウサイズの増大）は予測精度を高めると考えられるが, Transformer 系モデルでは入力系列を長くしても誤差が減少せず, むしろ悪化する場合もあるという結果が確認
4. 自己回帰デコーダの誤差累積問題
   • 多くのTransformerモデルは IMS（iterated multi-step） 方式, すなわち自己回帰的に一ステップずつ予測を重ねる構造を採用している.
   • これは予測誤差が累積しやすく、長期予測に不向き
   • LTSF-Linear のような DMS（direct multi-step）方式の方が安定性や精度で有利
5. 複雑・高コストな構造の割に有効性に疑問
   • Transformer 系統は Attention や多段構造により高いモデル容量と計算コストを要するが, 実験の結果からより単純なモデルの方が一貫して優れた性能を示すケースもあり, Transformer の選択に慎重さが求められるという示唆があります

一覧

課題	内容
順序性の欠如	Self-Attention の順序不変性により、時系列の並び情報が十分に反映されない。
予測性能の低さ	シンプルな線形モデル（LTSF-Linear）に比べ、Transformer は劣るケース多数。
長期依存の扱い	look-back window を増やしても精度が改善せず、逆効果なことも。
誤差累積	IMS方式の自己回帰デコーダは誤差の蓄積が避けられず、特に長期予測で不安定。
複雑さに見合う効果が薄い	複雑な構造・計算コストに見合う実質的な性能向上が得られていないことも。

https://arxiv.org/abs/2205.13504

iTransformer

Transformer系のモデルが,古典的な線形時系列モデルに負けるという事態はなぜ起こるのか？
その疑問に対して, iTransformerの著者らは, これまでのTransformerのアーキテクチャを変えないといけないということに気づいた.

そこで　"見方を変え"(inverted View) Transformerの構造を直したiTransformerを提案した.

上図はとてもわかりやすく, TransformerとiTransformerのトークン化の違いを説明している.

• （従来的な）Transformerの場合
  • 時系列データの関連性を算出する際に, 各時刻の値でトークン化していた
  • 例えば３つの時系列があるとき, 時間方向に時系列を区切ったある一時点における三つのデータには同じ時刻トークンを与える
• iTransformerの場合
  • 時系列データ全体をトークン化する
  • 例えば３つの時系列があるとき,それぞれの時系列に異なるトークンを与える

自然な発想では, （従来的な）Transformerの方が考えられそうだ.
一般的な時系列予測では過去の「時点」を要素として並べ未来の時点を予測するため, Transformerで付与するトークンも, 同じ時点でのデータに対し同じ時刻トークンをつけたらうまく予測できそうだ.

しかし, iTransformerでは発想を逆転し, 時系列データにおける「異なる変数（特徴量）間の関係性」に自己注意を向けることで, 精度を向上させた.

またこの構造により, 時系列変数間の相関関係もうまく捉えられるようになった.
なぜなら, クエリとキーの内積が時系列データ同士の相関, つまり, 変数間の相関を出力するものとなったからだ.

iTransformerは, Transformerを少し変えるだけで, 多変量時系列の予測タスクにおいて精度の向上ができるという, 簡便性と精度を備えた強力な手法として注目されている.

以下はiTransformerの理解に役立つだろう
https://zenn.dev/shungo_a/articles/1ae7e8c68b1cbb
https://zenn.dev/colorfulwave/articles/b5102c662051be

Minusformer

https://arxiv.org/pdf/2402.02332v2

さて, ひとつ話を進めて, iTransformerを改良したMinusFormer(Liang et al., 2024)

Transformer系およびiTransformerの課題として, 与えられた時系列データへの過学習が挙げられる.

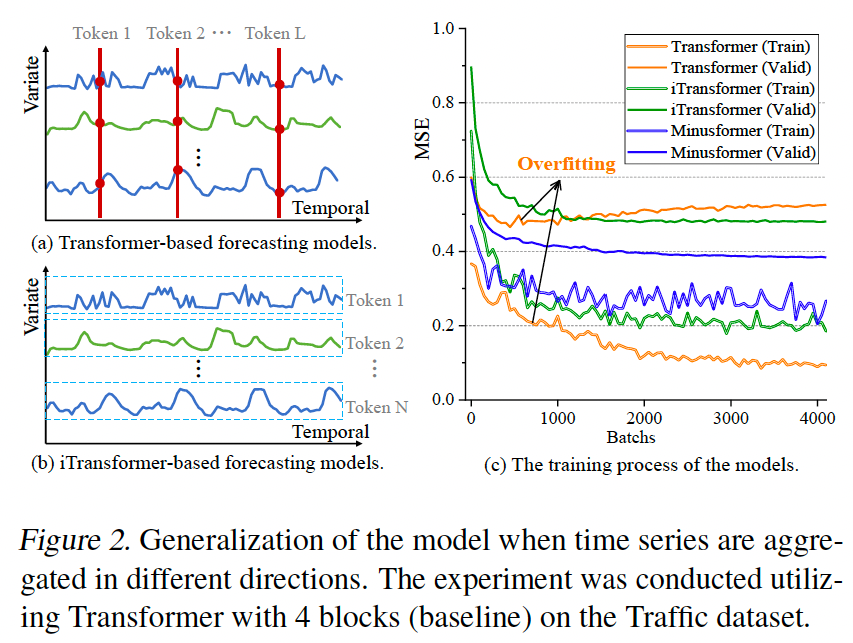
この問題を改善するため, 著者らは元のTransformerのアーキテクチャを変更した.
ただ, 変更したことは情報集約を「加法」から「減法」へ転換することやブロック図に補助的出力を導入 したシンプルな変更である.（以下の図を参照）

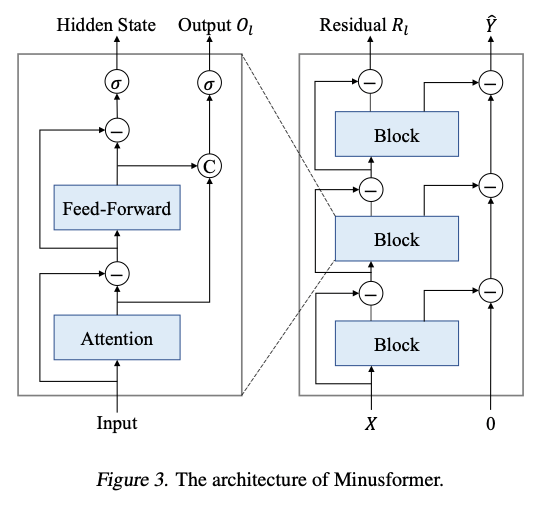
• 情報集約を「加法」から「減法」へ転換
  • 従来の Transformer では, 入力や出力を足し合わせて重ねていくスタイルが一般的だが、Minusformer では各層で “以前に学習した出力を差し引く” 方式 を採用
  • これにより, モデルは一層ずつ残差（supervision signal の差分）を学習していく逐次的な構造になる
• 補助的出力ブランチ（Auxiliary Output Branch）搭載
  • 各 Transformer ブロックに補助の出力経路を持たせ, そこからの出力を以降の処理から“引く”形で残差学習を誘導
  • これにより、学習過程が暗黙の漸進的分解（progressive decomposition）となり, モデルの 汎用性・解釈性・過学習耐性が向上

"減法" にしたということの裏返しとして, 加法だと「情報の重複蓄積」で過学習しやすいとされている. 具体的には, 同じ特徴やパターンが複数層で繰り返し蓄積され, 最終的に不要な高次ノイズまで強化されてしまう傾向がでてしまう. 特に時系列予測では, 過去データに含まれる短期的変動やノイズが強化され、過学習や外挿性能の低下につながる.

逆に減法だと, 現在の予測との差分（残差）だけを学習対象にできる. これはブースティング（Boosting）系の逐次残差学習 に近い発想で, 各層が「まだ学習していない部分」だけに集中できるため, 無駄な情報の重複を減らせる.

結果として, 減法は学習の進行方向を「誤差の削減」に揃えるため各層の役割が明確になるし,
出力を解析すれば「どの層でどの誤差を補正したか」が見えるためモデルの挙動が比較的解釈しやすくなるとされている.

観点	従来の加法的集約	Minusformer の減法的集約
情報蓄積	同じ特徴を繰り返し蓄積 → 重複・過学習のリスク	既に学習済みの成分を引く → 重複削減
学習効率	各層で全特徴を再学習する可能性	各層が残差のみを学習し、効率的
過学習耐性	特に深層化すると過学習しやすい	各層が過学習しづらく、汎化性能が向上
解釈性	各層の役割が不明瞭	各層が「何を減らしたか」が明確

まだまだ検証の余地はありそうだが, ひとつ進んだテクニックとして, 減法Transformerも知っていて損はないだろう.

まとめ

iTransformerと呼ばれるTransformer系の多変量時系列を中心に, 他のTransformer系モデルや古典的な手法との比較を行った.
個人的な勉強メモのつもりで用意したが, 誰かの何かの役に立てられることを祈る.

補足：transformer系のモデル一覧

iTransformerの論文で紹介されていたTransformer系統の手法について簡単に整理した.

興味があれば各自原論文をさらに読んでいってほしい.
また, 以下のスライドも参考にできる.

https://gochikika.ntt.com/_static/pdf/20240628.pdf

モデル	コアアイデア	強み	課題	iTransformer と比べて
iTransformer	「時刻ごとの多変量トークン」→変量（チャネル）をトークン化し, Attention で変量間相関を扱い, FFN を各変量内表現に適用（＝次元反転）	多変量相関の明示的モデル化, 高次元系列での性能・一般化, 任意のルックバック利用に強い. 解釈しやすいAttention	新手法ゆえ適用範囲・長期間の実装検証が今後必要.	変量中心の表現が強み（時系列側の patching/分解アプローチと対照的）
Vanilla Transformer	時刻ごとの「temporal token（多変量融合）」をAttentionで処理	並列化に強く長距離依存をキャプチャ可能。	トークンあたり多変量を混ぜるため変量間・時間内の役割混同、計算コスト（長系列）	iTransformerは「どの変数が重要か」がAttentionで明瞭になりやすい点で優位
Informer	ProbSparse attention（疎化）＋注意の蒸留＋一次推論で長系列効率化.	長系列での計算効率改善, 生成型デコーダによる高速推論.	近似／疎化の仮定が外れると性能低下, 変量表現の工夫は限定的.	iTransformer は変量トークン化で相関を直接学ぶため, 高次元多チャネルで可視化・性能が出やすい.
Autoformer	「系列分解（decomposition）」＋Auto-Correlation（自己相関ベースの依存検出）を導入.	長期予測で優秀、周期性検出に強く自己相関を効率的に扱う.	時系列の分解仮定が外れると弱い, 変量間相互作用は別途扱う必要あり.	iTransformerは変量間相関に直にAttentionする点で表現力が異なる（Autoformer は時系列側の構造を重視）
[FEDformer] (https://arxiv.org/abs/2201.12740)	周波数（Fourier 等）ベースの分解を入れて, 周波数成分を効率的に学習.	周波数ドメインで情報を集約→長期傾向・周期性の学習に有利, 計算効率も改善.	周波数表現が有効でないデータや非定常データでの一般化課題.	iTransformer は 時系列→変量の反転で多変量相関を重視するため, 周波数処理とは補完的な関係
PatchTST	時系列を「パッチ化（patch）」しチャネル独立・パッチ単位でTransformerを適用（channel-independent patching）.	パッチで局所情報を保持, 計算量削減と長履歴の利用に強い.チャネル独立でスケール良好.	パッチングで急激変動や短時間スパイクが失われる場合がある（パッチ化の設計依存）.	iTransformer はチャネル（変量）をトークンにする点で PatchTST の「チャネル独立」と近く, ただし iTransformer は変量間 Attention（相互チャネル相関）を明示的に学ぶ. PatchTSTは“同一重みを共有するチャネル独立”が特徴
TimesNet	1D 時系列を 2D テンソルに変換して, 2D 畳み込み的に「多周期性／2D変動」を捕らえる（TimesBlock）	多周期・多スケール変動を安定して捉え, 短長期・多タスクで堅牢	変換設計や2D化のハイパーパラメータが影響。変量間 Attention を直接使う設計ではない	iTransformer はAttentionにより「どの変数がどの変数に影響するか」を直接示せる点で異なる（TimesNet は変動構造の抽出に強い）
TFT (Temporal Fusion Transformer)	解釈性重視の構造（ゲーティング、選択、解釈可能な自己注意）と再帰的成分を組合せた多ホライズンモデル.	実務での解釈性・特徴選択が強み, 静的情報や既知未来変数の取り扱いが得意.	アーキテクチャが複雑で大規模化には手間, 純粋な長期依存の最先端性能では最近の LTSF モデルに劣る場合あり.	iTransformer は基本的に表現学習と相関可視化にフォーカスしており、TFT のような特化型解釈モジュールはない（要組合せ）
Crossformer	Dimension-Segment-Wise（DSW）埋め込みで時系列を変量×時間の2D構造として保持し, **Two-Stage Attention（時間→変量）**で依存関係を効率的に学習.	時間と変量の相互関係双方を効率的に捕捉。スケールの階層的処理	中間の「ルーター」を介し Attention を抑制するため、変量間依存の細部が失われる可能性あり。線形近似の範囲に依存	iTransformer は各変量を明確に Attention 対象（トークン）とし, Attention により直接相関を学習できるため, 解釈性や精密な変量間関係学習に強い
InParformer	Interactive Parallel Attention（InPar Attention） 導入. トレンド・周期分解モジュール＋時間／周波数ドメインでの並列依存学習 クエリ選択, KV圧縮・再構成で効率改善.	時間・周波数両面からの長期依存学習, 効率的計算, 分解モジュールによる複雑パターン捕捉.	複雑な構造（複数機構の統合）で実装・調整が難しく、タスク毎のモジュール設計が必要。	iTransformer の構造はシンプルかつ変量中心。Attention による直接的相関把握は InParformer にもあるが、InParformer は周波数構造の重視などで補完的な役割。

脚注

1. 特徴量という言葉をあえて使うとすれば, ひとつひとつの時系列が特徴量である. 船のセンシングデータでは, 計4つの特徴量を示してい, と言い直せる.

2. そのため, 計算量を文章の長さに応じずなんと定数時間に抑えている