テンポラル・ネットワークを味わう - テンポラルな距離の概念

概要

前回の記事では, テンポラル・ネットワークのデータ表現をいくつか紹介した.
今回は, そんなテンポラルなデータ表現を活用して, ネットワーク構造の大事な概念である「歩道」,そしてその主要な解析量である「距離」を紹介する.

静止したネットワークと違い, テンポラル・ネットワーク上では, 移動のために辿る枝が「時間によって発生したり, 消えたり」する. そのため, 目的の頂点へと向かうことができる枝が現れるのを待機する状態や, あるいは, タイミングによっては目的の頂点へ到達できない状態となったりする, というのが大きな特徴である.

そんな静止したネットワークと異なる, テンポラルな「歩道」, そして「距離」の定義について紹介する.

https://zenn.dev/akitek/articles/082d3353add444

静止したネットワークでの「道」と「距離」

まず静止したネットワークでの「道」および「距離」を定義する.
「歩道」(walk)とは, ある頂点から別の目的となる頂点までに, 隣接する頂点を経由して枝を辿って進む経路である. そして, 「道」は, ある頂点から別の目的となる頂点までに, 同じ頂点を通らずに, 進むことができる「歩道」である.
「歩道」は2頂点間の可能な経路を列挙するために, 「道」は2頂点間の最短経路を計算する上で便利である.

そして, 「距離」を, 2頂点間($v_i$と$v_j$)の「道」のなかで, 最小の移動回数（あるいは, 何らかの指標を最小にする）である. これを, $d(v_i, v_j$と定義する.無向ネットワークの場合,距離の公理が成り立つ.(逆に, 有向ネットワークでは一般的に非対称性が成り立たない)

1. 非負性: ($d(v_i, v_j) \geq 0$,
2. 非退化: ($v_i = v_j$のときにのみ, $d(v_i, v_j) = 0$ が成り立つ),
3. 対称性: ($d(v_i, v_j) = d(v_j, v_i)$),
4. そして, 三角不等式が成立する( $v_i$と$v_j$のとある「道」上の経由点$v_p$に対し, $d(v_i, v_j) < d(v_i, v_p) + d(v_p, v_j)$)

テンポラルな「道」と「距離」

次にテンポラルな「道」の定義を確認する.

テンポラル・ネットワークでは, 経路上の枝が, 時間によって発生したり, 消えたりしている. そのため, 2頂点間の道の一部がある時刻で消えている場合には, 移動がスムーズに行われないケースがある. その場合, 移動のために枝が発生する時刻まで待機することとなる.^[1]

また, タイミングによっては, 「道」が永久に途絶えてしまい, 目的の頂点に到達不可能な状態となる場合もある. つまり, テンポラル歩道は因果性をもつ道であり, 過去に発生した枝（イベント）の上を, 今歩いて移動することができない.

この因果性という制約のために, テンポラル・ネットワークの「歩道」は, 静止したネットワークとは全く別の性質を帯びることとなる.

以下, テンポラル歩道を表現する上で, イベント表現を利用する. イベント表現は, 枝リストに時間情報を含んだ$(u_i, v_i, t_i)$の集合で表せられる.

到達可能性行列

テンポラル・ネットワークでは, $v_i$から$v_j$までのテンポラル歩道が存在する場合, $v_i$から$v_j$は到達可能であるという. そうした到達可能の有無を整理したものが到達可能性行列 $R$である. $R$の$(i, j)$要素である, $R_ij$は, $v_i$から$v_j$へ到達可能であれば$1$, 到達不可能であれば$0$がはいる.

そして大事なことであるが, $R$は, 時間によって変化する. そこで, 時刻$t_i$以前のイベント表現を用いたテンポラル・ネットワークにおける到達可能性行列を, 添え字$t$を用いて$R_{t \leq t_i}$で表す.^[2]

図の例は, $v_1$から$v_4$へ移動する場合を考えたものである. まず, $R_{t \leq t_6}$, つまり, 時刻$t_6$までのイベント表現により構築されたテンポラル・ネットワーク上では, $v_1$から$v_4$へは到達可能になっている.

具体的には,計3つのテンポラル歩道があり, それぞれ${(v_1, v_2, t_1), (v_2, v_3,t_3),(v_3, v_4, t_5)}$と, ${(v_1, v_2, t_1), (v_2, v_4,t_6)}$と, ${(v_1, v_3, t_4), (v_3, v_4, t_5)}$である.

しかし, 使用するイベント表現が$t \leq t_4$までのもの,　つまり, $R_{t \leq t_4}$では, $v_1$から$v_4$へは到達不可能になっている.この場合, 時刻$t_5$以降に, 追加のイベントがなければ移動できない状態となっている.

時間によって到達可能性が変化していることを確認してもらえたらと思う. ちなみに, 一般的に到達可能性行列$R$は非対称である. つまり, $v_i$から$v_j$は到達可能であるとしても, $v_j$から$v_i$は到達可能である,...とは限らないのだ.

さまざまな「距離」

静止したネットワークと同様に, テンポラル・ネットワークにも「距離」を定義することができる. ところで, 静止したネットワークとは異なり, テンポラル・ネットワークでは, 枝が時間によって発生したり,消えたりする.

それにより, 前項の到達可能性行列では, テンポラル・ネットワークの構造を示すイベント表現の数が限定的となった場合, つまり, ある時刻から出発した, あるいは, ある時刻までに到達しなければいけない, というケースでは, 目的となる頂点に到達できなくなる可能性があることを述べた. 到達できない, ということは, その2頂点間の距離$d(v_i, v_j)$は, $\inf$ということになる.

このように, 状況によっては２頂点間の移動ができないことがあり, 2頂点間の距離も変動する.　つまりは, テンポラル・ネットワークでは, やはり, 「距離」も時間依存となる.

そして面白い特徴として, テンポラル・ネットワークでは, 最小距離を実現する歩道は道ではないかもしれない. つまりは,過去に通った2頂点間の枝を, 再度通る場合が, 最短経路となるケースがあるのだ. これは, 静止したネットワークではありえない.^[3]

以下テンポラル距離を三つあげる. 頂点$u$から頂点$v$へのテンポラルな道を${(u,v_1, t_1), (v_1, v_2, t_2),...,(v_{n-1}, v_n, t_n)}$のように表す.
また, 図の例と一緒に考えてみると理解が進むかもしれない.

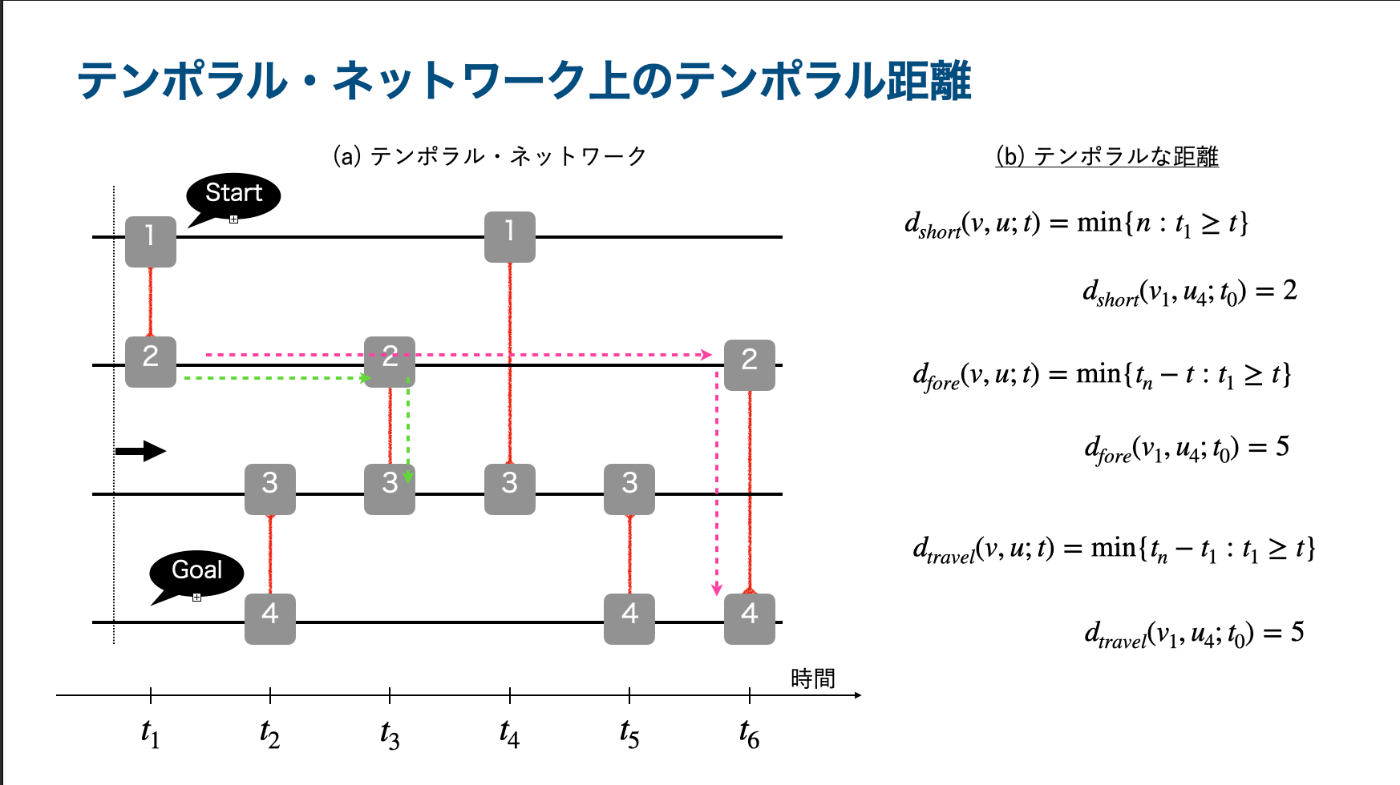
（テンポラル版の）最短距離

一つ目は, いわゆる, テンポラル・ネットワーク版の最短距離である. 静止したネットワークでは, 最短距離は, 二頂点間の移動に必要な最小の枝数である^[4]

テンポラル・ネットワークでも似たような概念が定義されている.

$$d_{short}(u, v; t) = \min \{n: t_1 \geq t\}$$

これは, 頂点$u$から, 頂点$v$にテンポラルな道に沿っていくために必要な最小の移動回数である. 後ろの${t_1 \geq > t}$は, 時刻$t$以降に出発すれば, との制約をつけている.

つまりは, 最短距離$d_{short}(u, v; t)$は, 時刻$t$によって変化するという時間変化を考慮していることになる. そして, 基本的には, 時刻$t$が時間的に後になるほど, テンポラルな枝の数がすくなるため, 移動可能なテンポラルな道が少なくなり, 結果として距離$d_{short}(u, v; t)$は単調に増加する^[5].

先頭距離

つぎは, 先頭距離(foremost distance)　である.これは,

$$d_{fore}(u, v; t) = \min\{t_n - t: t_1 \ geq t\}$$

と定義されている. ここで式に注目してほしいが, 最小化しているのは時間$t_n$である.つまり, 時刻$t$から数えて, 頂点$u$から頂点$v$まで行くのに必要な最小時間を評価している. はやく目的地まで到達できれば, 移動回数（テンポラルな道の長さ）には関心がない距離の測り方である.

旅行時間距離

三つ目は, 旅行時間距離である. 早速の定義であるが,

$$d_{travel}(u, v; t) = \min\{t_n - t_1 : t_1 \geq t\}$$

$d_{fore}$にも似た式であるが, 大きな違いとして, 最初の待機時間を無視していることである($t_1 - t$だけ). まさに, 移動中（旅行中）の時間だけを最小化しようというものである.

どれ使う？

３つのテンポラルな距離を紹介したが, 結局のところどれを使うと良いのだろうか？
答えは「ケースバイケース」となってしまう. なぜなら, それぞれ最小化しているものが違うため, 分析者の関心のある内容に合わせて適切な距離を選択する必要があるのだ.

各距離の違いについて, 『テンポラル・ネットワーク』(森北出版）では,わかりやすい例えを持ち出して説明してる.

例として, 公共交通ネットワークを考える. 枝は市内の駅と駅のつながりであるとする.
利用者が乗り換え愛数を最小化したいならd_{short}を用いるのがよい.
目的地になるべく早く到着したいのなら$d_{fore}$を使うべきだ.
移動中の時間をなるべく小さくしたいならば, $d_{travel}$を用いるべきだ.

なお, 無向ネットワークだとしても, $d(u,v;t) \neq d(v,u;t)$であり, 対称性は基本的に成りたたない.

時間に依存しない距離指標

テンポラルな道の最短距離$d_{short}$,先頭距離$d_{fore}$, そして, 旅行時間距離$d_{travel}$どれをとっても, 時間$t$に依存する指標であるとわかる.

しかし, 実用面では, 時間に依存しない, テンポラル・ネットワーク全体についての二頂点間の距離に興味があるかもしれない.
そんな時刻$t$に依存しない距離指標を作る方法は3つある.

1つ目は, 時間全体を通して最小値を用いる方法である. こうすれば, いつ移動を始めるか, という時間の縛りを受けず,テンポラル・ネットワーク全体でただひとつ求めることができる. 特に, 最短距離$d_{short}$,旅行時間距離$d_{travel}$に向いていて, それぞれ$\min_t d_{short}(u,v;t), \min_t d_{travel}(u,v;t)$を求めることとである.

2つ目は, 時刻$t$を, $t = 0$に固定してしまう方法である.こうすれば, 一つ目の方法と同様に, いつ移動を始めるか, という時間の縛りを受けず, 距離を定義できる.

3つ目は, 時間依存の距離指標を時刻全体にわたって平均する方法である.

ベクトル時計

最後に紹介するのは, 距離の定義から二頂点間で共有している情報の古さを測る, ベクトル時計である. もう少し詳しく述べると, 先頭距離の概念を用いることによって, 任意の頂点が他の任意の頂点についてどれだけ最近の情報をもっているかを定量化する.

テンポラルな視点

ベクトル時計を求めるため, 頂点$u$が頂点$v$について時刻$t$にもつ「テンポラルな視点(temporal view)」$\phi (u,v,t)$を定義する. この「テンポラルな視点」は, 頂点$u$から頂点$v$へ時刻$t$以前に到達するテンポラルな道が存在しうる最も遅いテンポラルな見市の出発時刻

少し定義の内容が難しく感じたかとおもうが, 要は, 時刻$t$にて頂点$u$が頂点$v$に持っている情報の取得時刻をもとめている. その求め方として, これまで時間方向にテンポラルな道をたどっていたものを, 時間方向とは逆の, 後ろ向きにみたテンポラルな移動距離（先頭距離）を計算しているに過ぎない.

ちなみに, 頂点$u$が頂点$v$に関する情報を取得するためには, 何も頂点$u$と頂点$v$とが直接やりとりをする必要はない. 過去に頂点$v$とやりとりがあった第三の頂点$k$から頂点$v$に関する情報を取得してもよいのだ. この場合,頂点$u$が取得する情報は, 過去に頂点$k$が頂点$v$とやりとりした時点のものとなることに注意が必要である.

テンポラルな視点$\phi (u,v,t)$がどのように求まるのか理解しやすいよう図を用意した.
図(a)は, 今回想定するテンポラル・ネットワークで, 離散時刻$[t_1, t_5]$での5回のイベントをもっている. イベント表現であれば, ${(v_1, v_2, t_1),(v_2, v_3, t_2),(v_1, v_3, t_3),(v_2, v_3, t_4),(v_1, v_2, t_5)}$となる.

ここで時刻$t_4$における, 頂点$v_1$が頂点$v_2$に関する情報の鮮度$\phi (v_1,v_2,t_4)$を求めてみよう. $\phi (u,v,t)$の定義に合わせて, 時刻$t_4$以前に,テンポラルな道を辿って, 頂点$v_1$から頂点$v_2$に到達できる先頭距離を探す.

すると, 図の点線矢印を辿ると, $(v_1, v_3, t_3) -> (v_2, v_3, t_2)$と枝を辿ることで, 点$v_1$から頂点$v_2$に到達できる. このとき, 点$v_1$は, 頂点$v_3$を経由して頂点$v_2$に関する情報を取得できる.ただし, 頂点$v_3$がもっていた頂点$v_2$に関する情報は, 時刻$t_2$のものなので, $\phi (v_1,v_2,t_4) = t_2$となる^[6].

情報潜時

そして$\phi (u,v,t)$が計算できると, 情報潜時(information latency) を求めることができる. これは, 頂点$u$が頂点$v$についての最も新しい情報を得てから現在までに経過した時間である. 情報潜時は, $t - \phi (u,v,t)$で定義されている. 図(b）を確認してほしい.

ベクトル時計と「前進」

さきほどは, 二頂点間の情報のやりとりに着目したが, それを拡張し, ある頂点$v_i$が時刻$t$にもつ他の頂点すべてについての最も新しい情報を集約したものをベクトル時計という.
つまり,

$$\phi (v_i,t) = (\phi (v_i,v_1,t)),(\phi (v_i,v_2,t)),...,(\phi (v_i,v_N,t))$$

そしてこのベクトル時計をつかい, 頂点$v$のベクトル時計$\phi (v,t)$の 「前進(advance)」 を定義できる. ここで, 「前進」は頂点$v$に関するベクトル時計$\phi (v,t)$のすべての要素にわたる和の, イベント$(u, v, t)$の直後と直前の差として定義される.

言い換えると, 「前進」はイベント$(u, v, t)$が頂点$v$にもたらす情報の定量化で, 「前進」の値が大きいイベントは価値が高いと考えることができる.

イメージとしては, イベント$(u, v, t)$を得ると, 時刻$t$で頂点$v$が頂点$u$を通じて, 頂点$u$自身, そして, 他の頂点の情報が更新される. この更新幅が大きいほど, 頂点$v$が頂点$u$は有意義であった, 大きな情報を頂点$v$にもたらしたと判定できる指標となっている. 頂点$u$が, 過去に頂点$v$以上に他の頂点とのやりとりをしていたとしたら, この頂点$u$を通して得られる情報も多くなるだろう.

まとめ

本記事は, テンポラル・ネットワークでの「距離」の定義や計算例を紹介した. テンポラル・ネットワーク上では, 二頂点間の距離の大きさが時間によって変化していた. また, 「距離」の定義もさまざまな指標が考えられることも特徴的である.

そして, そうしたテンポラルな距離を拡張し, 二頂点間での情報の鮮度を測るベクトル時計や, 情報潜時といった概念を紹介した.

距離が定義できたことで, いよいよネットワークの重要な量である「中心性」について説明できるようになった. 次回は, テンポラルな中心性を紹介するか, 今回が説明的な要素が多かったため, 先に「距離」やベクトル時計の計算アルゴリズムや実装例を紹介するかもしれない.

参考リスト

https://www.morikita.co.jp/books/mid/085702

脚注

1. まるで信号待ちかのようだ

2. この表現は本記事で勝手に定義している.時間の制約によって, さまざまな到達可能性行列がでてくる, と理解してもらえばそれでよい

3. 証明として, 一度通ったことのある頂点から, 冗長的な部分, 例えば, 1回目にその頂点を訪れてから, 2回目にその頂点を訪れるまでに通った歩道の部分を排除すれば, 移動距離は削減できるため.

4. 言うまでもないが, 枝に何らかの重みが定義されている場合は, その重みを最小にする経路が対象となる

5. 他の距離の定義でも同じだが, $t -> \inf$で, $d_{short}(u, v; t) -> \inf$となる. つまり, そもそものテンポラルな道がなくなる.

6. 他の時刻から計算した場合も載せているので各各人してほしい