テンポラル・ネットワークを味わう - テンポラルな表現方法

概要

前回の記事では, テンポラル・ネットワーク, つまり時間発展するネットワークの特徴について図表を用いて紹介した. 特に, 時間によってネットワークの構造が変化してしまうことによる, 情報伝達の非対称性が, 静止したネットワーク（以下、総計ネットワーク）との特筆すべき差異だと述べた.

https://zenn.dev/akitek/articles/31cf7ac40f3e11

本記事では, テンポラル・ネットワークの解析準備としてテンポラル・ネットワークのデータ表現について紹介する. 解析するためには, より解析しやすいデータ表現を用意することが重要であろう. それに加え, 「そもそもネットワークを時間の観点から記述できる」方法を知っておこう, という狙いである.

今回も, 『テンポラル・ネットワーク』（森北出版）を参考に, 適宜, スムーズな内容理解のために新規の図表を用意する.

https://www.morikita.co.jp/books/mid/085702

総計ネットワークでの従来表記法

テンポラル・ネットワークでの表現方法を紹介する前に, 従来の静止したネットワークでの表現方法を簡単に紹介する.

ネットワーク（あるいは、グラフ）は、頂点の集合($V$)と, 枝の集合($E$)を用いて次のように表現される.

$$G = (V, E)$$

このとき, 頂点数を$N$, 枝数を $M$で表す. そして, 各枝は, 二つの頂点で決まり, $e = (v, v' ) \in E$と表せる.

枝には向きがある場合があり,$(v, v') \neq (v', v)$と区別されているものを有向ネットワークと呼ぶ. 逆に, 枝に向きを考慮しない場合には, 無向ネットワークと呼ぶ.

以降は, 無向ネットワークを前提として話を進める.

従来の静止したネットワークの代表的なデータ表現としては, 隣接行列 $A$がある. これは, ネットワークを構成する頂点間のつながり, つまり隣接の有無を二値で表記した行列表現である.

$$\begin{equation} A_{ij} = \begin{cases} 1 & v_i\text{と}v_j\text{が隣接している} \\ 0 & \text{隣接していない} \\ \end{cases} \end{equation}$$

隣接行列の面白い性質として, 行列$A$の対角成分は$0$, そして,無向ネットワークであれば, 隣接行列$A$は対称な行列となる. つまり, $A_{i,j} = A_{j, i}$となっている.
そして, ネットワークのハブ分析などに使用される, 各頂点の次数$k_i$は, $k_i = \sum_{j}A_i$で求めることができる.

隣接行列は, 元のネットワークの構造に関する情報を漏れなく含めており, ネットワークを記述する主要なデータ表現である.

そんな強力な隣接行列であるが, ネットワークのサイズが大きくなると, 隣接行列$A$は,疎行列になる可能性が高く,無駄な計算量・記憶量を要求することになる^[1]

そうした計算面で有利なデータ表現として, 枝リストがある. これは, ネットワーク$G$内の$M$個の枝に関する集合リストとして表現される. 隣接行列と異なり, つながりがある箇所のみをデータとして列挙するため, ネットワークを記述するデータ表現として無駄がないのが特徴である.

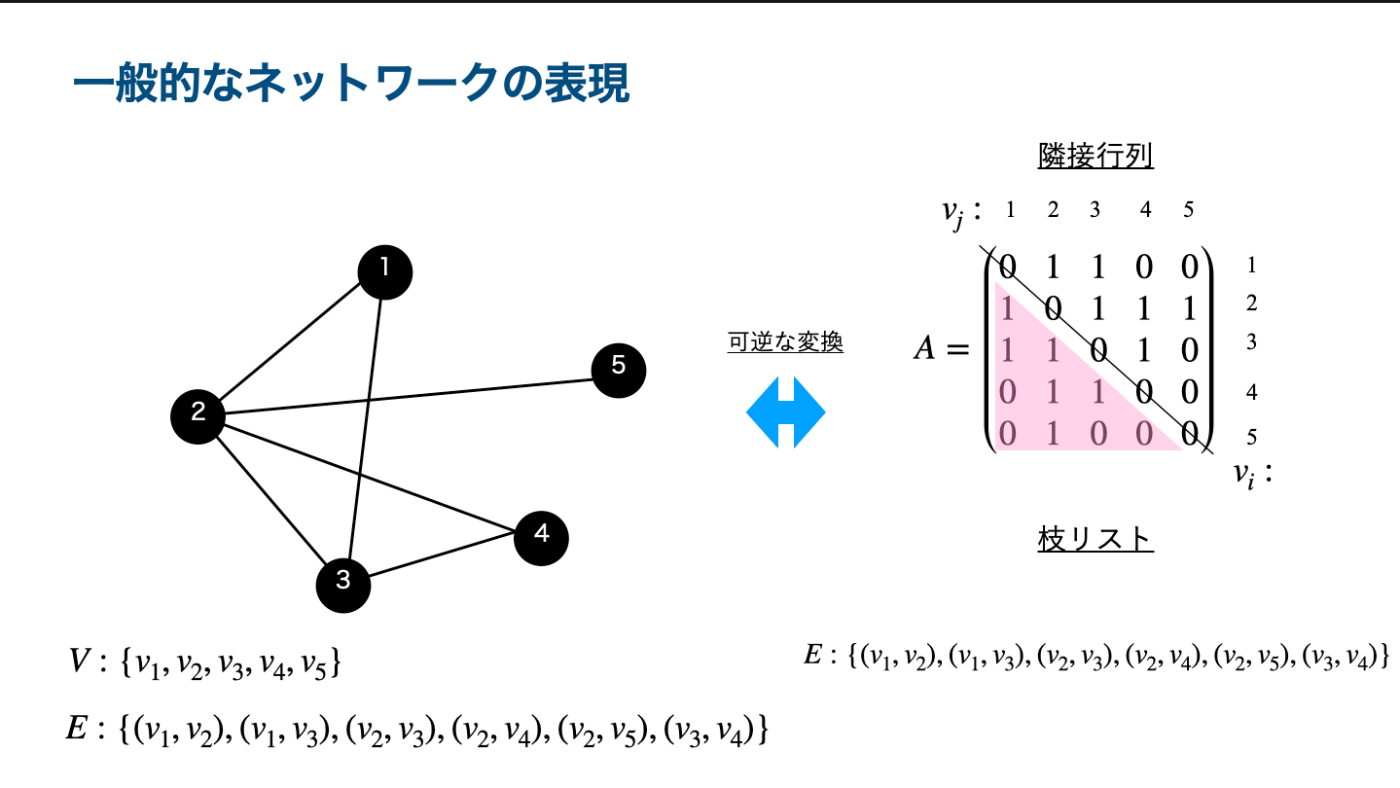
上図は, 頂点数 $N=5$ および　枝数 $M = 6$である向こうネットワークの一例である. 隣接行列$A$と, 枝リストは, それぞれ図中の表現となっていることを確認してほしい.

テンポラル・ネットワークのデータ表現

従来の静止したネットワークでのデータ表現を簡単に確認したので, 本題として, ネットワークの時間変化を考慮したデータ表現について確認していく. 書籍では, 『イベント表現』と『スナップショット表現』の主な紹介内容を用いる. もう少し発展的な表現方法である『ストリーム・グラフ』については, 書籍では詳細には述べられていないため, 図を用いてイメージしていただこう.

イベント表現

イベント表現は, 主にネットワークの枝に対し, 時間の概念を付与したものである. つまりは, 従来の枝の表記方法である $(v_i, v_j)$に変わり, 時間情報をもった枝表現では, $(u_i, v_i, t_i, \Delta t_i)$と表現される. これの読み方は, 時刻$t_i$において, 頂点$u_i$と, 頂点$v_i$とがつながりをもち, それが$\Delta t_i$だけの期間続いた, ことを示している.

つまりは, 頂点間のつながりが永続的なものではなく, タイミングによって発生したり, 継続したり, そして消えたりするという状態を表現しているとみなせる. 前回の記事で, 二者間のやりとりが時刻によって発生しているテンポラル・ネットワークを紹介した.そのときの言葉を再利用すると, 枝の発生をイベントとみなし, イベント時刻で時間順に並べたイベント列として表現したものが, イベント表現である.

$$\{(u_i, v_i, t_i, \Delta t_i); i = 1, 2, ...\}$$

改めて記号の定義を説明すると, $u_i$ と $v_i$ は, $i$番目のイベントがおこる枝をなす2個の頂点で, $t_i$は,$i$番目のイベントの生起時刻, $\Delta t_i$は $i$番目のイベントの継続時間である.

イベントの最終発生時刻を $t\_{max}$ とおくと, イベント表現は, イベントを時間方向に並べているため, $0 \leq t_1 \leq t_2 \leq \cdot \leq t_{max}$となる. 　イベントの継続時間$\Delta t_i$は, 通常イベントの間隔時間よりもとても短いため, 無視する場合も多い. そのような単純化を受け入れると, イベント表現は以下のようになる.

$$\{(u_i, v_i, t_i); i = 1, 2, ...\}$$

上図は, 頂点数 $N = 4$で, 最終時刻 $t\_{max} = 12$ までに発生した計14個のイベントを含むテンポラル・ネットワーク(a) および　そのイベント表現(b)を例示したものである. テンポラル・ネットワークでは, 頂点間のつながりは, 時間経過で発生するイベントとしてみなされる. イベント表現では, そうした時間情報を含んだ枝リストとして整理されている.^[2]

スナップショット表現

次に紹介するテンポラル・ネットワークのデータ表現は, あるタイミングでのネットワークの構造をそのまま表現するスナップショット表現である.

$$\mathscr{G} = \{ G(1), G(2), ..., G(t_{max}) \}$$

ここで, $t_{max}$はイベント表現では観測時間を示すが, スナップショット表現では時系列 $\mathscr{G}$に含まれるネットワークの数である.
あるいは, 静止したネットワークにおける隣接行列に似た表現として, あるタイミングでの隣接行列を, 添字の$t$をつけて定義できる.

$$\mathscr{A} = \{ A(1), A(2), ..., A(t_{max}) \}$$

ここで, $A_{ij}(t)$ は, 頂点$v_i$と頂点$v_j$が時刻$t (t = 1, 2,,...t_{max})$で枝をなすか否かを示す.上記の$G(t)$や $A(t)$を, テンポラル・ネットワークのスナップショットと呼ぶ.

次に具体的なスナップショット $G(t)$の作成方法を紹介する. 実は, テンポラル・ネットワークが離散時間のイベント表現で与えられれば, それを情報損失なしでスナップショット表現を獲得できる. 具体的には, 時間窓$T_w$を定義して, 長さ$T_w$の時間窓で, イベント表現のデータを集約することで, スナップショット表現が作成できる.

これについては, 例を確認したほうが理解が進むだろう.

上記の図では, さきにあげた14個のイベント表現を, $T_w = 3$の時間窓と,$T_w = 6$の時間窓により作成したスナップショット表現を載せている. $T_w = 3$の場合で説明すると, 時間窓の長さが$3$で, 観測時間が$12$なので, 計$4$個のスナップショットが作成される.

そして, $i$番目のスナップショットに含まれるイベント表現を, $(i-1) \times T_w \leq t_i < i \times T_w$ でまとめると, 図中の特定のタイミングでのスナップショットが作成される^[3]

例をみるとわかるが, スナップショット表現は, 各時刻においてネットワーク全体を見ることを強調した表現方法で, テンポラル・ネットワークを, ネットワーク構造が時間変化していくものとして把握している, といえる.

ストリーム・グラフ

書籍では具体的な図はないが, 面白い表現方法だと感じたストリーム・グラフを紹介する.

ストリーム・グラフは. 頂点集合$V$, 枝集合$E$, 時間範囲$T = [0, t_{max}]$として, テンポラルな頂点集合 $W \subset T \times V$や, テンポラルな枝集合$E \subset T \times V \otimes V$で表現する.

このように定義できると, 各頂点や枝が, ある時刻に存在しているかどうかをさらに定義できる. つまり, 頂点$v$が時刻$t$で現れるのは, $(t, v) \in W$のときただそのときのみで, 二つの頂点$v$と頂点$v'$間の枝が時刻$t$で現れるのは$(t, vv') \in E$のとき, ただそのときである.

このままでは, どういうことじゃ? と思われるが, 図（原著論文の例を書き直した）を参考にすると意味がわかるだろう.

この例では, 時刻$t = 10$までの, ４つの頂点($ |V| = 4$)を持つテンポラル・ネットワーク(つまり, $T = [0, 10]$)を示している. $W$はテンポラルな頂点の集合を示している. 例えば, 頂点$a$は, 時刻$0$から$10$までの間, ネットワーク上に存在している.

他方, 頂点$b$は, 時刻$4$から$5$の間では, ネットワーク上に存在していないことを示している.　図では,実線と点線で, 各頂点の存在期間を区別している. 同じことがテンポラルな枝$E$で表現されている.

ストリーム・グラフを使えば欲しい量を系統的に導け, 例えば, 頂点や枝がネットワークに現れる時間の集合を$T_v = \{(t, v) \subset W \text{を満たす} t\}$または$T_{vv'} = {(t, vv') \subset E \text{を満たす} t}$で表現できる. ここで, ある時刻で枝が存在するためには,枝を構成する頂点がどちらも存在していることを要求するため, $T_{vv'} \in (T_v \cup T_{v'})$となっていることは面白い.

その他, ストリーム・グラフの性質については,Latapy et al., 2017を確認してほしい. 図をもちいてとてもわかりやすく説明されている.

https://arxiv.org/abs/1710.04073

まとめ

本記事では, テンポラル・ネットワークのデータ表現について紹介した. データ表現では, 元のネットワーク構造の情報を落とさずに表現できることが求められる.静止したネットワークでは, 隣接行列や枝リストがあった.

テンポラル・ネットワークでは, それらに時間情報を組み込んだイベント表現や, スナップショット表現, そして ストリーム・グラフなどがある.

• イベント表現では, テンポラル・ネットワークの枝リストを, ある時点で発生するイベントとして再定義した
• スナップショット表現はそのイベント表現を一定期間まとめ, ネットワーク全体の時間変化を捉えたもの
• ストリーム・グラフは, テンポラルな頂点や枝を時間との集合表現で示したものであり, 特にテンポラルな頂点, つまりは, ネットワーク上で頂点が発生したり, 消えたりするという概念は, イベント表現やスナップショット表現にはない独特な表現方法である

ここまでの内容でテンポラル・ネットワークの表現方法をいくつか確認できた. 次回以降は, テンポラル・ネットワークの具体的な解析量として, 長さや中心性の扱っていけたらと思う.

雑記

書籍を読んだとき, テンポラルなネットワークをどのように表現するのかイマイチわかっていなかった. いろいろと表現する方法はあるだろうが, 大事なのは, 元のネットワーク構造の情報を極力失わず, かつ今後の解析処理に適した形式で表現できることが望ましいだろう. そうした観点では, イベント表現やスナップショット表現など, （正直なところ）従来の静止したネットワークではなじみのない, テンポラル・ネットワークに独特な表現形式を導入されていることは新鮮かつ納得できた.

脚注

1. ネットワークのサイズ$N$に対し, 枝の数 $M$ がそこまで増えないという事態のことを示す. 身近な例にも多くあるだろう.

2. つまりは, 静的ネットワークにおける枝リストに対応するデータ表現といえよう.

3. 書籍とスナップショット表現が異なるが, 各スナップショットの境界条件に違いによる...