【線分交差】GISを作るデータ構造とアルゴリズム【計算幾何学】

概要

前回の記事では, GISの基本機能のひとつ,「凸包計算」を実装した. 計算幾何学のなかで培われてきた幾何情報へのアルゴリズムの美しさの一端が見えたかと思う.

今回から, より実用的なGIS機能に合わせた処理を考えていく.まずは, 「地図の重ね合わせ」 である.

GISを使っているといくつかの地図データ（レイヤー） を重ねて,新たなデータを作ったり分析したりすることがある.例えば, 異なる災害のハザードマップの重ねて, 自分が住んでいるエリア・街の被災リスクを検討することが挙げられる.

以下は国土交通省が公開している「重ねるハザードマップ」の例である.

洪水・内水のハザードマップ

津波のハザードマップ

こうした「地図の重ね合わせ」処理について実装していこうと思う.
重要なテクニックとして, 地物のポリゴンを「二重辺リスト」と呼ばれるデータ構造で表現し, 「平面走査法」と呼ばれるアルゴリズムを用い, 「地図の重ね合わせ」に関わるさまざまな処理を効率的に解いていることだ.

今回はそのうちの「平面走査法」を説明する.
今回も「コンピュータ・ジオメトリ　第3版　計算幾何学：アルゴリズムと応用」を参考にしていく.

https://www.kindaikagaku.co.jp/book_list/detail/9784764903883/

地図の重ねあわせ

「地図も重ねあわせ」の簡単な例をみながら, アルゴリズムの入力と出力についてまずは考えていこう.
いま下図のような図形$P$と図形$Q$を使った重ね合わせの処理を実装したい.

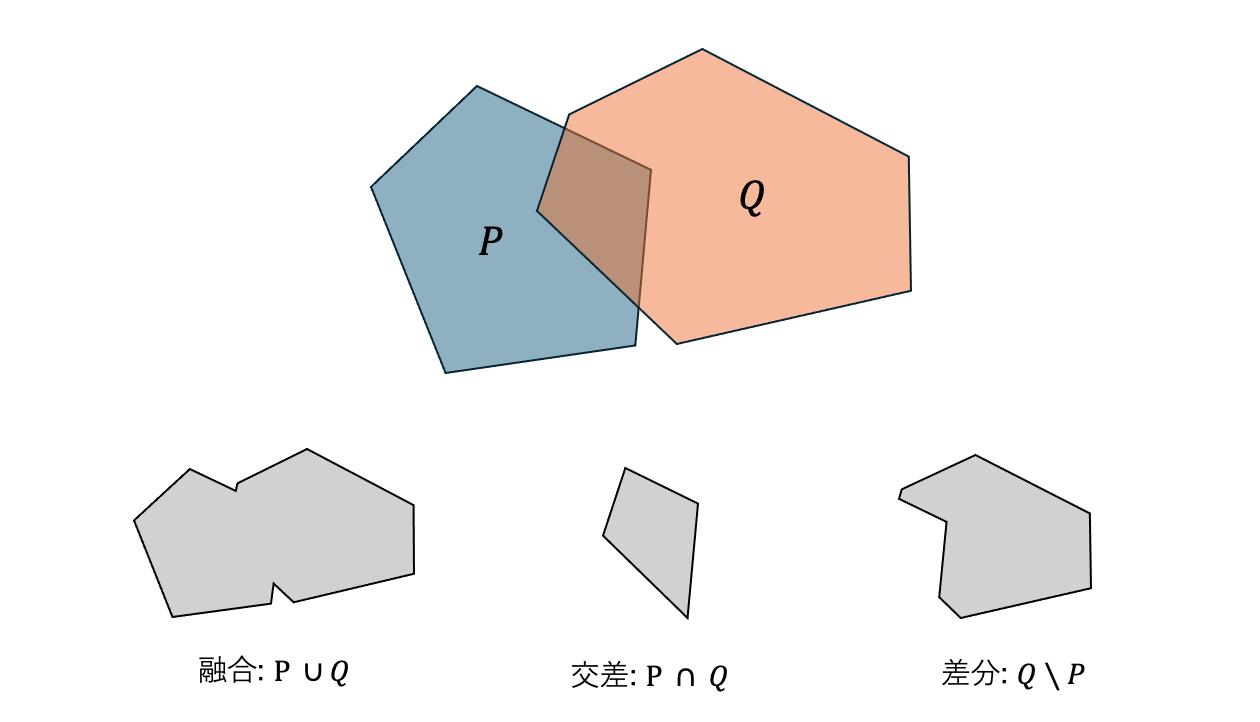
重ね合わせには, 「融合」「交差」「差分」といった種類の処理方法がある. 目的に応じて処理後の図形の形も変わっていることがわかる.^[1]

ここで考えたいことは,どのようにしたら「融合」「交差」「差分」といった「重ねあわせ」の処理が実装できるか, ということだ.
どのように「処理」するかの前に, どのような「出力」であれば目的合うかを考えてみよう.

ポイントは, 前回の記事で扱った「凸包」がそうであったように, 「重ね合わせ」後の図形（=領域）は, 点集合により表現できることにある.

改めて図形$P,Q$の頂点に番号を振り, そして２つの図形の交差点を$A,B$とおく.
すると, 「重ねあわせ」の処理の入出力は次のようにすべて点集合で表現できる.

• 入力: 図形$P=[p_1,p_2, ..., p_5]$, 図形 $Q=[q_1,q_2,...,q_6]$
• 出力：
  • 融合: 図形$[p_1,p_2,A, q_2, ..., B, p_4,p_5]$
  • 交差: 図形$[q_1,A, p_3, B]$
  • 差分: 図形$[A, q_2, ..., q_6, B, p_3]$

注目してほしいのは, どの「重ねあわせ」方法であっても, ２つの図形の交差点を$A,B$が出てきうるということだ. 「重ねあわせ」の処理において, 異なる図形間での交差点は重要な情報である.

そして, 処理への入力時にはまだ交差点の情報が入っていないことから, 「重ねあわせ」の処理のどこかで交差点を求める必要がある.

本記事は, その「交差点」を求める方法に焦点を当てよう.
わかりやすくするため, 図形を複数の線分の集合とみなし, 交差点は異なる図形に含まれる線分同士の交差により発生する, ものとしてアルゴリズムを考えよう.

線分交差

素直なやり方

前段で, 「地図の重ねあわせ」処理において, 異なる図形間での交差点を求める(あるいは, 交差するかどうかも含め）必要があると述べた.

シンプルな方法は, すべての線分の組み合わせで交差点の判定および交差点の座標を求める方法だ.いわゆる総当たり法（=ブルートフォース） と呼ばれるものだ.

言わずもがな, この方法はシンプルすぎるが故に, 大規模なデータにはとてもじゃないほどの計算コストがかかる.なぜなら, 総当たり法の計算量は$0(n^2)$のオーダーである.

地図のデータは, 何千,何万という線分をもつデータに平気でなりうる. そのため, $0(n^2)$で求まるアルゴリズムでは耐えられないだろう.

よく考えると, 線分が交差するケースはそこまでないはずだ. ある線分が,他のすべての線分のうち, 交差する可能性があるものはそもそもとても少ないはずで, 計算の対象をかなり削減できるはずである.

ここでは, 実行時間が入力の線分数だけではなく, 交点の個数にも依存するようなアルゴリズムがほしいのである. こうしたものを, 出力サイズに敏感なアルゴリズムという. できるだけ無駄を排した計算方法を探したいのだが, そのヒントが「幾何学的な特徴」に隠れている.

平面走査法

「幾何学的な特徴」といえば, 何よりも座標から求まる「距離」がイメージできるだろう.
線分が交差するには,そもそも線分同士が近くなければ発生し得ない...と考えることはできないだろうか.

簡易的な方法で, 線分の長さ,つまり, ２頂点をy座標に投影してみると, なんとなく線分が交差する線分のペアが絞られてくる.(下図）

下図では,線分$A$と線分$B$はy軸上で重なっているので交差の可能性はありそうだ!^[2] 逆に, 線分$A$と線分$C$はy軸上で重なっていないので,はじめから交差の可能性はないだろう.

y軸上に各線分を投影することで, そもそも交差する線分のペアを限定できそうだ!
つまり, y軸上での区間が重なりをもつような線分対だけを, つまり両方の線分と交わる水平線が存在するような線分対だけを調べたらよい, ことになる.

そこで, どの線分のy軸よりも高い位置から低い位置へ移動する走査線$l$を導入し, y軸上での区間が重なりをもつような線分対を調査していく処理を考える. このようなアルゴリズムを平面走査法(Plane Sweep algorithm) と呼ぶ.

具体的には, 走査線$l$は, 走査線$l$と交差する線分集合を状態(これを走査線状態とよぶ)として保持し, その集合内に含まれる線分だけで交差判定をしていく.

もちろん走査線$l$はy軸に沿って移動するため, 走査線状態も逐次更新される. ただ, 更新のタイミングは連続的ではなく, 線分の端点に重なったときのみでよい. こうした更新タイミングにかかわる点をイベント点とよぶ.^[3]

上図でイメージをしてもらう. 走査線状態の更新タイミングとして,

1. 線分上端に走査線が通ったとき
2. 線分下端に走査線が通ったとき

のふたつのイベント点が重要である.
1)の場合, この線分を走査線状態に加え, 既存の走査線状態内の線分との交差判定に利用する.2)の場合い, この線分を走査線状態から排除し, 以後, 交差判定には使わないようにする.

上図でもう少し口語的に述べると,

1)走査線$l$が線分$s_{k}$の上端に触れたとき, 走査線状態に線分$s_{k}$を加え, 走査線状態内の線分集合$[s_j,s_i,s_p]$との交差判定を行う.
2)今度は走査線$l$が線分$s_{j}$の下端に触れたとき, 走査線状態から線分$s_{j}$を排除し, 以降走査線状態内に加えられる他の線分との交差判定を回避させる.

上記の方法でうまくいけるかなー🧐と思うも, 実は意地悪な例もあり, その場合には総当たり法との優位性が出てこなくなる. 例えば, 下図の左のように, y軸方向に並行な線分がほどよく範囲を共有している場合だ. 実際には交点が一つもないのに, かなりの数の交差判定を要求される.

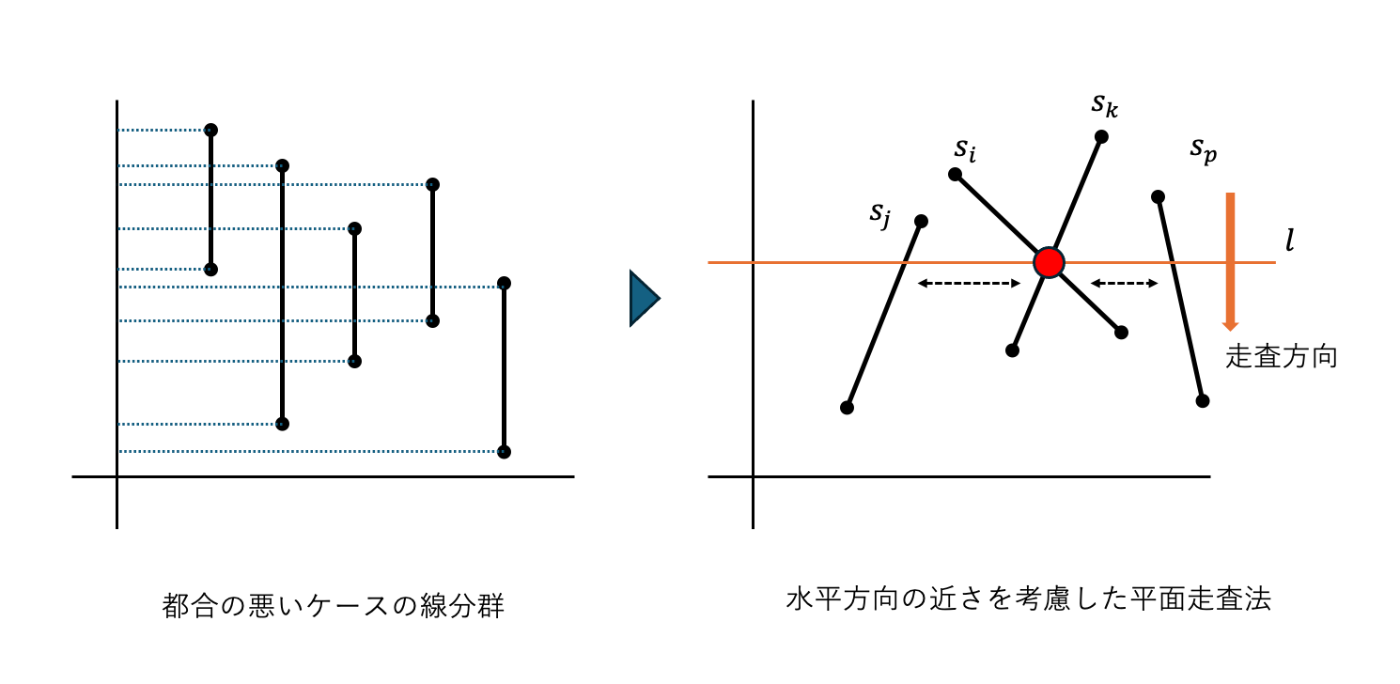
そこでさらに改良が加えられ, 水平方向の近似性を交差判定に考慮されるようにする.
つまり, x軸方向で隣接している線分同士のみで交差の判定をすることで, さらに無駄な処理を減らす.

すると,走査線状態としては単なる線分集合ではなく, 各線分の隣接関係を保持できるものに変える.

そして, 走査線状態の更新タイミングとして,

1. 線分上端に走査線が通ったとき
2. 線分下端に走査線が通ったとき
3. (New)交差点に走査線が通ったとき

の3つのイベント点が重要である.さらに, 3番目の"交差点"をイベント点を考慮しはじめているのに注目だ.

それぞれ, 1)において, この線分を走査線状態に加え, 既存の走査線状態内の線分との隣接関係を更新し, その後, 交差判定に利用する. 2)において, この線分を走査線状態から排除し, 走査線状態内の線分との隣接関係を再更新する. 3)において, 交差点前後で, この交差点をつくる２つの線分の左右関係が変化することから, 走査線状態内の線分との隣接関係を更新する.

上図でもう少し口語的に述べると,

3.について, 線分$s_i,s_k$の交差点を走査線が通ると, $s_i,s_k$の位置関係は, $[s_i,s_k]$から,$[s_k,s_i]$へと入れ替わる. すると, 線分$s_j$の右隣接の線分が, 線分$s_i$から線分$s_k$へと変化する. 他も同様である.

これならうまくいきそうだ. これらを整理して,必要なデータ構造とアルゴリズムを用意しよう.

データ構造とアルゴリズム

イベントキューと走査線状態構造

それでは必要なデータ構造から定義していく.
平面走査法では,走査線状態の更新タイミングはイベント点にあると述べた. つまり, イベントキューではこれらのイベント点を格納し, 走査線状態の更新のトリガーを管理させる.

キュー$Q$には, イベント点として線分の端点を全て格納する. この時, 線分の端点を, 走査線の向きに合わせて自動的に並べ替えると便利だろう.

例えば, 走査線がy軸の大きい方向から小さい方向へ移動する場合, キュー$Q$では, y座標の大きな端点が先頭に来るように管理する. 同じy座標の時は, さらにx座標が小さいものを優先するなどの大小関係を明確に定義しておこう.

そして, イベント点は平面走査法の処理過程で増えることもある. つまり, 交点が発見された場合だ. 交点がイベント点として重要な意味を持つことは先に述べたとおりである.
よって, キュー$Q$に交点をイベント点として追加・更新できる仕組みも必要だ. もちろん, 用済みの端点・交点をキューから除外する処理も導入する.

キューには,単なる点座標だけでなく, その点がどの線分のものか, そして,その点が始点・終点・交点のどれかを管理しておこう. これらの情報は, あとで定義する状態構造ツリーの操作にて重要な情報となる.

pythonであれば, headqライブラリを使用すると簡単に優先度付きキューを実装できるのでおすすめだ. headqライブラリそのものの説明は以下の記事たちに任せる.

https://qiita.com/ell/items/fe52a9eb9499b7060ed6
https://qiita.com/T_Wakasugi/items/dac6eb77a3cace54f95e

イベントキュー実装例

from heapq import heappush, heappop, heapify

class EmptyQueueException(Exception):
    def __str__(self):
        return "Cannot pop an empty queue"

class PriorityQueue:
    '''
    各イベント点を管理し　逐次処理をサポートするキュー
    '''
    def __init__(self):
        self.queue = []
        self.dup = set()

    def __str__(self):
        return '[' + ' '.join([str(i) for i in self.queue]) + ']'

    def isEmpty(self):
        return len(self.queue) == 0

    def pushAll(self, l):
        for a in l:
            self.push(a)

    # for inserting an element in the queue
    def push(self, e):
        if e.status != "int": # 交点以外なら素直にキューに入れる
            heappush(self.queue, e)

        elif e not in self.dup: # 交点であり, まだ未登録であれば追加（異なる線分での同じイベント点を重複登録するのを避ける）
            heappush(self.queue, e)
            self.dup.add(e)

    def __len__(self):
        return len(self.queue)

    def pop(self):
        if self.isEmpty():
            raise EmptyQueueException()
        else:
            return heappop(self.queue)

    def __iter__(self):
        """
        Do ascending iteration for TreeSet
        """
        for element in self.queue:
            yield element

    def clear(self):
        self.queue = []

次に,線分の隣接関係を記録する状態構造$T$ である.
隣接関係という言葉からわかるように, ある線分の左隣の線分, 右隣の線分という二つの情報を記録する必要がある. とすれば, 平衡２分木が便利であろう.

このツリーが更新されるタイミングは, イベントキュー$Q$からイベント点を取り出した時と同じで, それぞれ取り出されたイベント点の意味によって異なる処理へ分岐させる.

1. イベント点が線分の始点の時： 状態構造$T$にイベント点を始点とする線分$s$を加える.
2. イベント点が線分の終点の時： 状態構造$T$にイベント点を終点とする線分$s$を除外する.
3. イベント点が線分間の交点の時： 状態構造$T$上で, イベント点を構成する２つの線分の位置を交換（Swap)する.

どの処理であっても, ツリー上で隣接関係が変動し, イベント点に関連する線分を中心とした隣接する線分との交差判定を実施する.　もし, 交差判定により交点が見つかった場合には, イベントキュー$Q$へと格納する.

平衡２分木については, pythonでのbisectライブラリを使用するのが良いだろう.
こちらも以下の記事たちにライブラリの説明は任せる.
https://qiita.com/seigot/items/5091499d75a11cc77e41
https://qiita.com/T_Wakasugi/items/c979e977f56531942de4

状態構造の実装例

import bisect

class TreeSet(object):
    """
    bisectを用いた２分木データ構造
    各セグメントの大小関係を管理させる
    """
    def __init__(self): # 初期化
        self._treeset    = []
        self.pop_number  = 0
        self.push_number = 0

    def isEmpty(self):  # 空判定
        return len(self) == 0

    def addAll(self, elements): # treesetにない要素であれば追加
        for element in elements:
            if element in self: continue
            self.add(element) 

    def add(self, element):
        if self.isEmpty() or element not in self:
            bisect.insort_right(self._treeset, element)
            self.push_number += 1

    def add_high_low(self, element): # ツリーに新しい線分を追加
        if element not in self: # 未登録であれば
            index = bisect.bisect_right(self._treeset, element)
            self._treeset.insert(index, element) # 新規挿入

            low = self._treeset[index - 1] if index > 0 else None
            high = self._treeset[index + 1] if index < len(self._treeset) - 1 else None
            self.push_number += 1 # ツリーサイズの更新
            return low, high # 両隣の線分を返す

        return None

    def push(self, element):
        self.add(element)

    def pushAll(self, l):
        for a in l:
            self.push(a)

    def pop(self):
        if not self.isEmpty():
            res = self._treeset[0]
            self._treeset = self._treeset[1:]
            return res
        return None

    def higher(self, e): # 与えられた値よりも大きいtreesetのうち最小のものを返す(つまりセグメントeのお隣)
        index = bisect.bisect_right(self._treeset, e)
        if index < self.__len__():
            return self[index]
        else:
            return None

    def lower(self, e): # 与えられた値よりも小さいtreesetのうち最大のものを返す(つまりセグメントeのお隣)

        index = bisect.bisect_left(self._treeset, e)
        if index > 0:
            return self[index - 1]
        else:
            return None

    def swap(self, e1, e2): # treeset内の要素を交換
        i1                = self._treeset.index(e1)
        i2                = self._treeset.index(e2)
        self._treeset[i1] = e2
        self._treeset[i2] = e1

    def __getitem__(self, num): # treeset[i]
        return self._treeset[num]

    def __len__(self):
        return len(self._treeset)

    def clear(self):
        """
        ツリーを空にする
        """
        self._treeset     = []

    def remove(self, element):
        """
        指定した要素をツリーから排除する
        """
        try:
            self._treeset.remove(element)
        except ValueError:
            return False
        return True

    def __iter__(self):
        """
        繰り返し処理
        """
        for element in self._treeset:
            yield element

    def __str__(self):
        return '[' + ' '.join([str(i) for i in self._treeset]) + ']'

    def __eq__(self, target):
        if isinstance(target, TreeSet):
            return self._treeset == target._treeset
        elif isinstance(target, list):
            return self._treeset == target

    def __contains__(self, e): # e in self の処理
        """
        Fast attribution judgment by bisect
        """
        try:
            return e == (self._treeset[bisect.bisect_left(self._treeset, e)])
        except:
            return False

擬似プログラミング

---

アルゴリズム: $FindIntersections(S)$
入力：　平面上の線分集合$S$
出力: $S$の線分間の交点の集合

1. イベントキュー$Q$を空に初期化する. 次に線分の端点を$Q$に挿入する. 線分の上端点を挿入するときは, 対応する線分も一緒に蓄えること
2. 状態構造$T$を空に初期化する.
3. while $Q$が空ではない.
4. ---- do $Q$における次のイベント点$p$を求め,それを削除する.
5. ---- $HandleEventPoint(p)$

---

アルゴリズム: $HandleEventPoint(p)$

1. $U(p)$を$p$を上端点とする線分の集合とする; これらの線分はイベント点$p$と一緒に蓄えられている.
2. $T$上で$p$を含むすべての線分を求める. それらは$T$において隣接している.これまでに見つけた線分のうち, $p$を下端点とする線分集合を$L(p)$とし, これまでに見つけた線分のうち, $p$をその内部に含む線分の集合を$C(p)$とする.
3. if $L(p) \cup U(p) \cup C(p)$が２本以上の線分を含んでいる.
4. ---- then $p$を交点として報告し, 同時に$L(p), U(p), C(p)$も出力する.
5. $L(p) \cup C(p)$の線分を$T$から排除する.
6. $U(p) \cup C(p)$の線分を$T$に挿入する. $T$における線分の順序は$p$のすぐ下の走査線と交差する順序に対応していなければいけない.
7. ($C(p)$の線分を削除して再び挿入すると, 順序が逆転する)
8. if $U(p) \cup C(p) = 0$
9. ---- then $T$において$p$のすぐ左とすぐ右の線分を$s_l, s_r$とする.
10. -------- $FindNewEvent(s_l, s_r,p)$
11. ---- else $T$において$U(p) \cup C(p)$の左端の線分を$s'$とする.
12. -------- $s_l$を$T$において$s'$の左端の線分とする.
13. -------- $FindNewEvent(s_l, s',p)$
14. -------- $T$において$U(p) \cup C(p)$の右端の線分を$s''$とする.
15. -------- $s_r$を$T$において$s''$の右端の線分とする.
16. -------- $FindNewEvent(s'',s_r,p)$

---

アルゴリズム: $FindNewEvent(s_l,s_r,p)$

1. if $s_l$と$s_r$が走査線より下で交差するか, 走査線上でかつ現在のイベント点$p$の右で交差し, しかもその交点はイベント点としてまだ$Q$にはない.
2. ---- then この交点をイベント点として$Q$に挿入する.

---

具体例

最後に, 一体全体平面走査法のなかで, イベントキュー$Q$や状態構造$T$がどのように変化しているのかをイメージしてみる.

下図の左のような線分集合に対し交点を求めていく. それぞれ走査線の位置が,$l,l',l''$の場合のイベントキュー$Q$や状態構造$T$の中身を右側で示している.

走査線位置$l$では,処理開始前の段階で, イベントキュー$Q$は, 線分集合を構成する線分の端点をイベント点として蓄えている.^[4]

走査線位置$l'$へと移動すると, 端点4,6がイベントキュー$Q$から出てきて, 状態構造$T$にて,これらの端点を抱える線分集合$s_1,s_2,s_5,s_6,s_7$による隣接関係がツリー上で構築される. その後,隣接する線分同士で交差判定を行う.結果として, 線分$s_1,s_2$間で交点9が見つかり, イベントキュー$Q$へ格納される.

ここで重要なのは, まだこの状態では線分$s_1,s_5$間では隣接関係になっていないので, 交点10は見つかっていないことである.

その後, 走査線位置$l''$へと移動すると, 線分$s_1,s_2$の位置関係が代わり, 線分$s_1,s_5$間では隣接関係となって, 交点10が発見される.

まとめ

今回は「地図の重ねあわせ」処理に必要な交点を見つけるアルゴリズム「平面走査法」について説明した. 次回は, アルゴリズム「平面走査法」を駆使し, いよいよ「地図の重ねあわせ」処理へと拡張していく.

P.S.
プログラムコードについては必要であれば公開する予定である. かなり長くなるので記事に載せることは避けた. 兎にも角にも, 第二章の段階で高度な話になってきていて辛い🥹

脚注

1. illustratorのような描画ツールでもお馴染みだ

2. 実際は交差しないのだが, 可能性としては候補に残しても良いだろう

3. なので, 実際には走査線$l$自身を一定間隔移動させるのではなく,走査線$l$を線分の各端点の高さまでワープさせるような離散的な動かし方になる.

4. 走査線の位置に合わせて,蓄えられる端点のIDがソートされていること, 複数の線分を構成する端点は複数回格納されていることに注意. 同じ端点のIDであっても,それぞれが所属する線分や始点・終点の位置付けが異なるため区別できる.