【凸包】GISを作るデータ構造とアルゴリズム【計算幾何学】
概要
地理空間情報システム(GIS)は, いまや都市計画, 防災, 経済学, 生物学...さまざまなドメインで不可欠な地理空間情報の可視化・分析ツールとなっている.
有名なGISツールではArcGISがあるし, 無料で利用できるQGISはお世話になったひとも多いだろう.
GISを使ってできる地理空間情報を扱うが, もう少し定義を広げ, 「地理空間情報を幾何学的構造」[1]とみなすと, 今後は「計算幾何学」という研究分野がみえてくる.
逆に, GISはこの「計算幾何学」の理論やアルゴリズムを活かし, 幾何学的構造をもつ地理空間情報に基づく問題を効率的に解いている.
いまとなっては,内部のそういった処理をユーザーが直接見る機会はないかもしれない.[2]
ただ, 今一度**GISが実装している機能を支えるデータ構造やアルゴリズムを学ぼう!!**という記事である.
この手の話を, 日本語で読める書籍は以下の「コンピュータ・ジオメトリ 第3版 計算幾何学:アルゴリズムと応用」だけだと思っている.[3]
この本の内容に添いつつ, 有名どころの幾何学アルゴリズムをわかりやすく, かつ実装例をまとめたいいとおもう.
今回は, 基本的な処理である「凸包計算」である.
凸包とは
凸包計算は,
"ある点集合Pに対し,それらを内包する最小の凸領域" を求めることである.
イメージをもってもらうため, 「輪ゴムと釘」の例を持ち出す.
板に打ちつけた複数の釘に対し, それらをすべて囲むように輪ゴムを広げて手を離す.
輪ゴムが元のサイズに戻るときに, いくつかの釘にゴムがひっかかるはずだ. この時できたゴムの形こそすべての釘を囲む最小凸包領域である.

凸包計算の最終成果物のイメージができたところで,計算的にはどんな入出力なるのか考えよう.
幾何学アルゴリズムなので, 入力に対し, どのような処理で, 出力があるという3つの定義が必要だ.
入力は点集合であり, 出力は最小凸包領域,,,であるが, もう少し厳密に定義したい.
図を見ると, 実は最小凸包領域は元の点集合の部分集合で示せることがわかる.
つまり,
- 入力: 点集合
{p_1, p_2, ..., p_9} - 出力:最小凸包領域
{p_1, p_2, p_6,p_9,p_8,p_4}
よって, 処理にあたる凸包計算は, 入力となる点集合のなかから, 複数の点を結ぶことで最小凸包領域を構成できる元の点集合の部分集合を探す, こととなる.
最後, もう少し概念的な部分を説明する.
そもそも「凸(convex)とは🧐?」という部分だ.
本の言葉を持ってくると,
平面の部分集合Sが凸(convex)であるための必要十分な条件は, Sの中の任意の点
に対し, 線分 p,q が \bar{pq} に完全に含まれることである. S

次に説明するアルゴリズムでは点と点を結んでいく処理が入るが, その際に破ってはいけないルールがこの凸性である.
アルゴリズム
では, 具体的に凸包を求めるアルゴリズムを説明していく.
ここでは, 逐次構成法(incremental algorithm) による, ある点集合Pを内包する最小の凸領域を求める.
以前, 「凸包計算は入力となる点集合のなかから, 複数の点を結ぶことで最小凸包領域を構成できる元の点集合の部分集合を見つける」と説明した.
逐次構成アルゴリズムでは, 入力となる点集合
擬似プログラミング
入力: 平面上の点P
出力: CH(P)の頂点を時計回りの順に並べたリスト
- 点を
x p_1,p_2,...,p_n - リスト
L_{upper} [p_1, p_2] - for i <- 3 to n:
- ---- do
p_i L_{upper} - -------- while
L_{upper} L_{upper} - -------- do 最後の3点のうちの中央の点をリスト
L_{upper} - リスト
L_{lower} [p_n, p_{n-1}] - for i <- n-2 downto 1:
- ---- do
p_i L_{lower} - -------- while
L_{lower} L_{lower} - -------- do 最後の3点のうちの中央の点をリスト
L_{lower} -
L_{upper} L_{lower} -
L_{lower} L_{upper} L - return
L
まず凸包の計算では,入力となる二次元上の点を
ソート後の点集合のうち,
そこで,
見ればわかるが, 一点一点を処理し, 凸包の解を更新していることがわかる.
更新時, (5,6)のように, "最後の3点が右回りではない"という判定による点の除去もされている.
この判定による点の除去のイメージを共有しておこう.
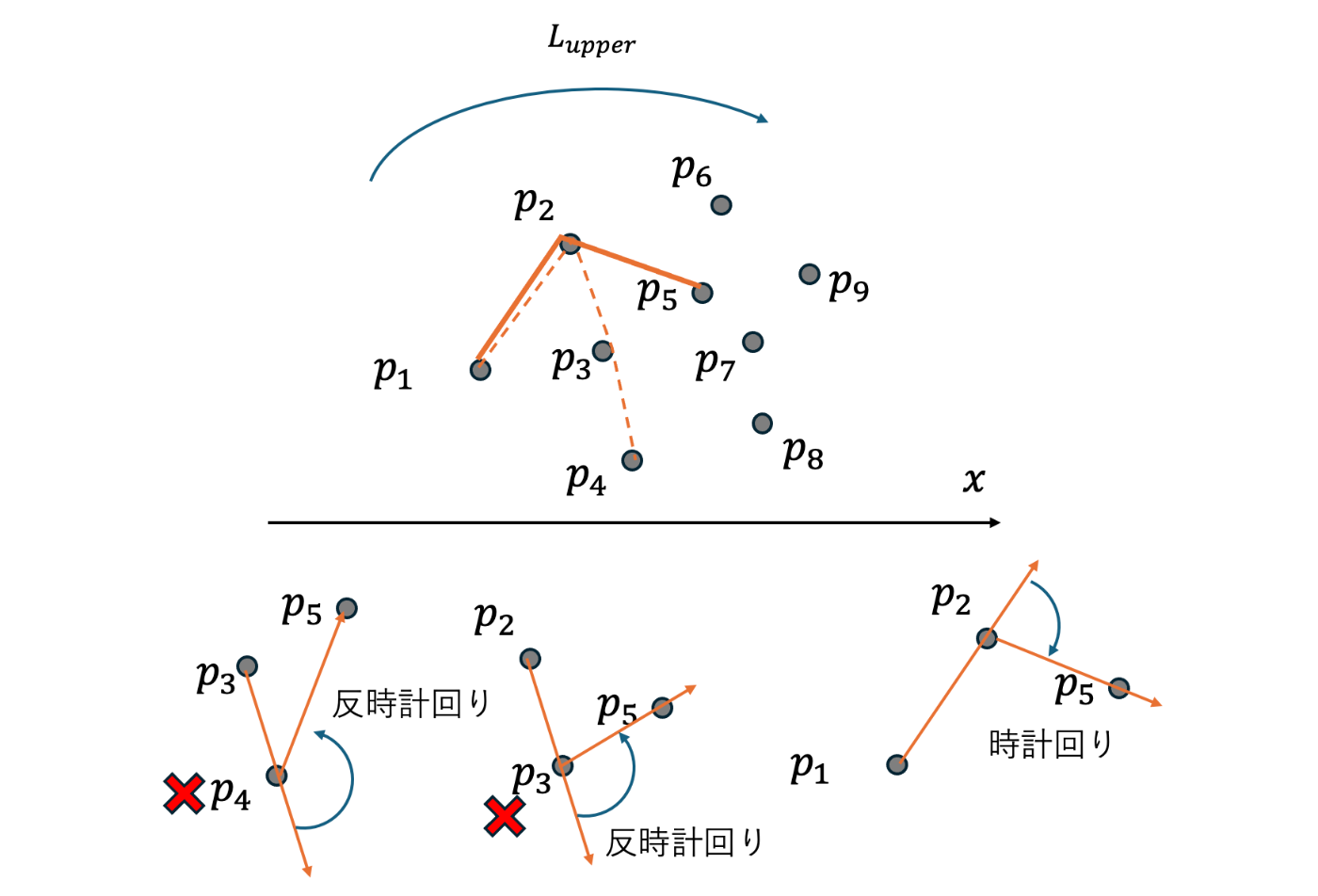
上の図は,
まず,
ここで"右回り(=時計回り)"といっているのは, ベクトル
ベクトル
逆に, ベクトル
結果として,
Pythonコード
さてPythonでの簡単な実装例を挙げておこう.
import random
import numpy as np
import matplotlib.pyplot as plt
P = np.random.uniform(0, 10, (10,2)) # 0-10の範囲で10個の点をランダム生成
xP = np.argsort(P[:,0], axis=0)
SP = P[xP]# X座標でソート
def judge_clockwise(L): # 右回り判定処理
# p,q,r:numpy.narray = [x1,y1],[x2, y2],[x3,y3]
p,q,r = L[-3], L[-2], L[-1]
v = q - p
u = r - q
o = v[0]*u[1] - v[1]*u[0] # 外積の計算
if o >= 0:
return True
else:
return False
# 上側凸
Lu = [SP[0], SP[1]]
step = 2
while step < len(SP):
Lu.append(SP[step]) # 点の追加
while len(Lu) >=3 and judge_clockwise(Lu):
Lu.pop(-2) # 後ろから2番目を排除
step += 1
# 下側凸
np = len(SP)
Ll = [SP[np-1], SP[np-2]]
step = 2
while step < len(SP):
Ll.append(SP[np-step-1]) # 点の追加
while len(Ll) >=3 and judge_clockwise(Ll):
Ll.pop(-2) # 後ろから2番目を排除
step += 1
# プロット
fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(1,1,1)
ax.scatter(P[:,0],P[:,1])
for i in range(len(Lu)-1):
ax.plot([Lu[i][0],Lu[i+1][0]],[Lu[i][1],Lu[i+1][1]], color='orange', linestyle='solid')
for i in range(len(Ll)-1):
ax.plot([Ll[i][0],Ll[i+1][0]],[Ll[i][1],Ll[i+1][1]], color='green', linestyle='solid')
ax.set_xlim([0,10])
ax.set_ylim([0,10])
ax.set_title('xy-points')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set(aspect=1) # 縦横比の指定
ax.grid(True) # グリッドの表示
fig.show()

まとめ
今回は, GISで使用されている基本処理のひとつ「凸包」を実装した. GISで使用されているデータは, 幾何学アルゴリズムにより効率的かつ頑健に処理できる.
次回は, GISで頻繁に使用される, 「地図の重ね合わせ」処理を支える「平面走査法」を紹介できればと思う.
Discussion