🐈
Qiskitを使った量子最適化アルゴリズムの応用へ〜パート1 量子計算の基礎〜

Victor Von Pooh
2025/03/26に公開
＊この記事はQiita記事の再投稿となります。
こんにちは！

株式会社アイディオットでデータサイエンティストをしています、秋田と申します。

このシリーズは、量子最適化アルゴリズムを具体的な問題に対して使うことによって、量子コンピュータのユースケースとしてどんなものがありそうかを妄想することを目的に、量子コンピュータの基礎から学ぼうというものになります。

その上で、IBM社が開発している量子コンピューティング用SDKのQiskitの使い方を学びながら、どのように量子計算が行われているのかを体験しましょう！

また参考までに、以前行った「初めてQiskitを使ってからQiskitで量子機械学習ができるようになるまで」シリーズも是非見てみてください(バージョン的に古いかもですが...)。

本記事と同様の実験をGoogle Colaboratoryで簡単に出来るように、このプロジェクトのGitHubリポジトリにノートブックを作成しました。

 量子コンピュータとは
 量子コンピュータのオリジンそもそも量子コンピュータとは、一体どのようなコンピュータなのでしょうか。

量子コンピュータの対比として、従来のコンピュータを古典コンピュータなどと言いますが、簡単に言うと「量子力学の理論に基づいたコンピュータ」のことです。

物理学の世界では、ニュートンが落ちるリンゴを見て運動方程式を見つけたような古典力学の他に、ミクロな世界でのみ適用されるような説明が難しい現象を取り扱う量子力学というものがあります。

これらは自然現象を解明するために日々研究されている分野になりますが、同時にコンピュータというものも自然を模倣するように考えられています。

古典コンピュータが古典力学を反映させているのだとしたら、量子力学に対応するようなコンピュータがあっても良いだろうという考えから生み出されたのが量子コンピュータです。

 量子コンピュータは万能なの？ここで何となく想像していただきたいのですが、古典力学では説明がつかないようなことが量子力学では起きているということは、あくまでも古典力学でカバーしきれない理論を量子力学で補っているという関係があり、それをそのまま古典・量子コンピュータの方にも持ってきています。

すなわち、量子コンピュータが古典コンピュータの完全上位互換ということではなく、古典コンピュータでは難しかったことでも量子コンピュータなら計算できるかもしれないと仮説を立てるレベルの話になります。

実際に、量子コンピュータにも得意・不得意な計算は存在し、もっと言うとどんな分野で量子計算が役に立つのかということがほとんど分かっていないのが現状です。

そこで、最適化の分野で量子コンピュータの優位性が見られるのではないかと研究が盛んに行われているのですが、このシリーズのゴールとしては、その最適化の分野における量子コンピュータのユースケースが無いかを探ることになります！

 量子計算量子コンピュータで行う計算を「量子計算」と言います。

量子計算を行うための「ビット」に相当するのが「量子ビット」です。

その量子ビットの状態を変化させるのに必要なのが「量子回路」です。

 量子ビット古典コンピュータでは、ビットは 0 と 1 のみで、それを \text{AND}, \text{OR}, \text{NOT} などの論理ゲートを通して計算を行っていました。

一方で、量子コンピュータでは、量子状態 |0\rangle や |1\rangle を重ね合わせた状態を、量子回路内にある量子ゲート(パウリゲートやアダマールゲート、CNOTゲートなど)を通して変化させて計算を行います。

重ね合わせ状態とは、次のような線型結合した状態を表します。

| \psi \rangle = \alpha |0\rangle + \beta |1\rangle
ここで、 \alpha, \beta は次のような条件を満たす複素数です。

|\alpha|^2 + |\beta|^2 = 1
まずは簡単な量子状態 |0\rangle, |1\rangle について、次のように定義します。

|0\rangle := \begin{pmatrix} 1 \\ 0 \\ \end{pmatrix}, \quad |1\rangle := \begin{pmatrix} 0 \\ 1 \\ \end{pmatrix}
つまり、 1 量子ビットの量子状態というのは、 2 次の複素ベクトルとして表現することができるということです。

よって、一般的な量子状態 | \psi \rangle は次のように表すことができます。

| \psi \rangle = \alpha |0\rangle + \beta |1\rangle = \alpha \begin{pmatrix} 1 \\ 0 \\ \end{pmatrix} + \beta \begin{pmatrix} 0 \\ 1 \\ \end{pmatrix} = \begin{pmatrix} \alpha \\ \beta \\ \end{pmatrix}
さらに、 1 量子ビットの量子状態はBloch球と呼ばれる球体の球面上の点の位置にマッピングさせることができます。
では、 2 量子ビット以上になるとどうなるでしょうか？

量子状態 |00\rangle, |01\rangle, |10\rangle, |11\rangle はそれぞれ次のように定義されます。

\begin{aligned}
    |00\rangle &:= \begin{pmatrix} 1 \\ 0 \end{pmatrix} \otimes \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix}, \quad
    |01\rangle := \begin{pmatrix} 1 \\ 0 \end{pmatrix} \otimes \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix}, \\
    |10\rangle &:= \begin{pmatrix} 0 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix}, \quad
    |11\rangle := \begin{pmatrix} 0 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix}
\end{aligned}
ここで、 \otimes という記号は、テンソル積を表しています。

テンソル積の計算は次のようなものになります。

\begin{pmatrix} \alpha \\ \beta \end{pmatrix} \otimes \begin{pmatrix} \gamma \\ \delta \end{pmatrix} = \begin{pmatrix} \alpha \begin{pmatrix} \gamma \\ \delta \end{pmatrix} \\ \beta \begin{pmatrix} \gamma \\ \delta \end{pmatrix} \end{pmatrix} = \begin{pmatrix} \alpha \gamma \\ \alpha \delta \\ \beta \gamma \\ \beta \delta \end{pmatrix}
n 量子ビットの場合、このテンソル積を使えば少ない量子ビットでの量子状態から表現が可能になるということです。

このとき、ベクトルの次数は 2^n となります。

 量子回路量子回路は、様々な量子ゲートを組み合わせて量子状態を変化させるための一連の流れを図式化したものになります。

まずはどのような量子ゲートがあるかを見てみましょう。

1 量子ビットゲートとして有名なものとして、以下の3種類を紹介します。
パウリゲート

X ゲート

Y ゲート

Z ゲート

I ゲート

アダマールゲート
回転ゲート

R_x ゲート

R_y ゲート

R_z ゲート

まずはパウリゲートですが、それぞれ次のように定義されます。

\begin{aligned}
    X &= \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}, \quad
    Y = \begin{pmatrix} 0 & -i \\ -i & 0 \end{pmatrix}, \\
    Z &= \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}, \quad
    I = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}
\end{aligned}
これらの量子ゲートをパウリゲートと言い、それぞれ量子状態 |0\rangle, |1\rangle に対して次のように作用します。

\begin{aligned}
    X &:
    \left\{
        \begin{array}{l}
            |0\rangle \rightarrow |1\rangle \\
            |1\rangle \rightarrow |0\rangle
        \end{array}
    \right., \quad Y :
    \left\{
        \begin{array}{l}
            |0\rangle \rightarrow i|1\rangle \\
            |1\rangle \rightarrow -i|0\rangle
        \end{array}
    \right., \\
    Z &:
    \left\{
        \begin{array}{l}
            |0\rangle \rightarrow |0\rangle \\
            |1\rangle \rightarrow -|1\rangle
        \end{array}
    \right., \quad I :
    \left\{
        \begin{array}{l}
            |0\rangle \rightarrow |0\rangle \\
            |1\rangle \rightarrow |1\rangle
        \end{array}
    \right.
\end{aligned}
続いて、アダマールゲート(H ゲート)は次のように定義されます。

\begin{aligned}
    H &= \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}, \\ \\
    H &:
    \left\{
        \begin{array}{l}
            |0\rangle \rightarrow \frac{1}{\sqrt{2}}\left(|0\rangle + |1\rangle\right) \\
            |1\rangle \rightarrow \frac{1}{\sqrt{2}}\left(|0\rangle - |1\rangle\right)
        \end{array}
    \right.
\end{aligned}
ここまでに定義された5種類の量子ゲートは、定義から次のことが言えます。

X^2 = Y^2 = Z^2 = H^2 = I
最後に回転ゲートですが、それぞれ次のように定義されます。

\begin{aligned}
    &R_x(\theta') =
    \begin{pmatrix}
        \cos\left(\frac{\theta'}{2}\right) & -i\sin\left(\frac{\theta'}{2}\right) \\
        -i\sin\left(\frac{\theta'}{2}\right) & \cos\left(\frac{\theta'}{2}\right)
    \end{pmatrix}, \notag \\
    &R_y(\theta') =
    \begin{pmatrix}
        \cos\left(\frac{\theta'}{2}\right) & -\sin\left(\frac{\theta'}{2}\right) \\
        \sin\left(\frac{\theta'}{2}\right) & \cos\left(\frac{\theta'}{2}\right)
    \end{pmatrix}, \notag \\
    &R_z(\theta') =
    \begin{pmatrix}
        e^{-i\frac{\theta'}{2}} & 0 \\
        0 & e^{i\frac{\theta'}{2}}
    \end{pmatrix}
\end{aligned}
ここで、 \theta' はBloch球上の各軸を起点にどれだけ回転させるかの角度を表しています。

量子状態 |0\rangle, |1\rangle に対しての作用はそれぞれ次のようになります。

\begin{aligned}
    &R_x(\theta') :
    \left\{
        \begin{array}{l}
            |0\rangle \rightarrow \cos\left(\frac{\theta'}{2}\right)|0\rangle - i\sin\left(\frac{\theta'}{2}\right)|1\rangle \\
            |1\rangle \rightarrow -i\sin\left(\frac{\theta'}{2}\right)|0\rangle + \cos\left(\frac{\theta'}{2}\right)|1\rangle
        \end{array}
    \right., \\
    &R_y(\theta') :
    \left\{
        \begin{array}{l}
            |0\rangle \rightarrow \cos\left(\frac{\theta'}{2}\right)|0\rangle + \sin\left(\frac{\theta'}{2}\right)|1\rangle \\
            |1\rangle \rightarrow -i\sin\left(\frac{\theta'}{2}\right)|0\rangle + \cos\left(\frac{\theta'}{2}\right)|1\rangle
        \end{array}
    \right., \\
    &R_z(\theta') :
    \left\{
        \begin{array}{l}
            |0\rangle \rightarrow e^{-i\frac{\theta'}{2}}|0\rangle \\
            |1\rangle \rightarrow e^{i\frac{\theta'}{2}}|1\rangle
        \end{array}
    \right.
\end{aligned}
今度は 2 量子ビットゲートとして有名なものを1つ紹介します。

テンソル積の考えをベクトルから行列に拡張することにより、 1 量子ビットゲート U, V のテンソル積 U \otimes V を | \psi_0 \rangle \otimes | \psi_1 \rangle に作用させられる 2 量子ビットゲートが作れます。

一方で、元から 2 量子ビットに対して作用させるための量子ゲートも存在し、その1つがCNOTゲートです。

\begin{aligned}
    \text{CNOT} &= \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix}, \\ \\
    \text{CNOT} &:
    \left\{
        \begin{array}{l}
            |0\rangle \otimes |0\rangle \rightarrow |0\rangle \otimes |0\rangle \\
            |0\rangle \otimes |1\rangle \rightarrow |0\rangle \otimes |1\rangle \\
            |1\rangle \otimes |0\rangle \rightarrow |1\rangle \otimes |1\rangle \\
            |1\rangle \otimes |1\rangle \rightarrow |1\rangle \otimes |0\rangle
        \end{array}
    \right.
\end{aligned}
この作用を見ると、1つ目の量子ビットが |0\rangle のときは2つ目の量子ビットに何もせず、1つ目の量子ビットが |1\rangle のときは2つ目の量子ビットを反転させていることがわかります。

この参照している1つ目の量子ビットのことを制御量子ビット、またはコントロール量子ビットと呼び、反転させる2つ目の量子ビットをターゲット量子ビットと呼びます。
さて、ここで量子計算特有の「量子もつれ」というものを作ってみましょう。

これは古典計算では非常に作るのが難しい状態ですが、上で定義されてきたことを踏まえると簡単に出来てしまいます！

その前に、一度テンソル積について見直しましょう。

先ほど2つの 1 量子ビットのテンソル積を定義しましたが、このテンソル積で表現できる状態のことを積状態と言います。

一方で、 1 量子ビットのテンソル積のみで記述できない状態も存在し、これらを量子もつれ、またはエンタングルメントと言います。

例えば、次のような 2 量子ビットの状態があると考えてみましょう。

| \psi_0 \rangle \otimes | \psi_1 \rangle = \begin{pmatrix} \alpha \gamma \\ \alpha \delta \\ \beta \gamma \\ \beta \delta \end{pmatrix} = \frac{1}{\sqrt{2}} \left(|00\rangle + |11\rangle\right) = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 0 \\ 0 \\ 1 \end{pmatrix}
この等式が正しい場合、 \alpha \gamma = \frac{1}{\sqrt{2}}, \alpha \delta = 0, \beta \gamma = 0, \beta \delta = \frac{1}{\sqrt{2}} が同時に成り立つ必要があります。

\alpha \delta = 0 より \alpha, \delta は複素数なので \alpha = 0 または \delta = 0 です。

ここで、 \alpha = 0 であるならば、 \alpha \gamma = \frac{1}{\sqrt{2}} は成り立ちませんし、 \delta = 0 であるならば \beta \delta = \frac{1}{\sqrt{2}} が成り立ちません。

よって4つの等式を同時に満たすことはできないため、状態 \frac{1}{\sqrt{2}} \left(|00\rangle + |11\rangle\right) は2つの 1 量子ビットのテンソル積で表せないことが分かりました。

この量子もつれをベル状態と言います。

ベル状態にはいくつか種類があり、次のようなものです。

|Bell\rangle = \frac{1}{\sqrt{2}} \left(|00\rangle \pm |11\rangle\right), \quad \frac{1}{\sqrt{2}} \left(|01\rangle \pm |10\rangle\right)
このベル状態を作る量子回路を作ってみましょう。

まず、 2 量子ビット |00\rangle を用意し、片方の量子ビットにアダマールゲートをかけます。

(H \otimes I) |00\rangle = \frac{1}{\sqrt{2}} \left(|00\rangle + |10\rangle\right)
次に、アダマールゲートを作用させた方の量子ビットを制御量子ビットとしてCNOTゲートを作用させます。

\text{CNOT}_{0, 1} \frac{1}{\sqrt{2}} \left(|00\rangle + |10\rangle\right) = \frac{1}{\sqrt{2}} \left(|00\rangle + |11\rangle\right)
このとき、 |00\rangle では制御量子ビットが |0\rangle なので何も変化しませんが、 |10\rangle では制御量子ビットが |1\rangle なのでターゲット量子ビットが反転し、 |11\rangle となります。

また、 \text{CNOT}_{0, 1} は 0 番目の量子ビットを制御量子ビットに、 1 番目の量子ビットをターゲット量子ビットにすることを意味しています。

3 量子ビット以上の2種類の量子もつれが起こる状態を一般に、Greenberger, Horne, Zeilingerの3名の頭文字をとってGHZ状態と呼びます。

 Qiskitを使ったプログラミングここからは、いよいよQiskitを使って量子計算をしてみましょう！

まずはGoogle Colaboratoryの環境下にQiskit系のライブラリをダウンロードして使えるようにします。
!pip3 install qiskit[visualization] qiskit-ibm-runtime qiskit-aer
これでライブラリが使えるようになりましたので、早速プログラムを組んでみましょう！

 量子回路の作成まずはライブラリのインポートからしましょう。
# ライブラリのインポート
from qiskit import __version__, QuantumCircuit
from qiskit.transpiler.preset_passmanagers import generate_preset_pass_manager
from qiskit.visualization import plot_histogram
from qiskit_aer import AerSimulator, StatevectorSimulator
from qiskit_ibm_runtime import QiskitRuntimeService, SamplerV2
# Qiskitバージョン確認
print(__version__)
ここでは量子回路を実際に作ってみます。

まずは量子ビットを用意して、量子ゲートを作用させる方法を紹介します。
# 1量子ビットの量子回路を作成
qc_0 = QuantumCircuit(1)

# X, Y, Z, Hゲートの作用のさせ方
qc_0.x(0) # Xゲートを作用させる
# qc_0.y(0) # Yゲートを作用させる
# qc_0.z(0) # Zゲートを作用させる
# qc_0.h(0) # Hゲートを作用させる

# 量子回路を図(画像)で表示
qc_0.draw("mpl")
簡単に解説しますと、 QuantumCircuit クラスのインスタンス qc_0 は、
qc_0 = QuantumCircuit(1)
より 1 量子ビットの量子回路の基盤を作るというものになります。

ここで引数を 2 や 3 に変更することにより n 量子ビットの量子回路を作成することができます。
続いて、この量子回路インスタンスに対してゲートを作用させるには、 qc_0.x(0) のように対応するメソッドを実行します。

この場合、 X ゲートを作用させるという意味になり、引数 0 は 0 番目の量子ビットに作用させるということになります。

もちろん今回は 1 量子ビットの量子回路なので、 1 以上の引数を入れるとエラーが発生します。

他にも量子ゲートを作用させる方法はあるのですが、少しややこしいのでまずはこれで慣れるようにしましょう。
そして、出来た量子回路を表示するのが draw() メソッドになります。

引数には "mpl" や "latex"などのオプションがあります。

今回は画像として表示/保存できる "mpl" を用いています。
では、先ほど学んだベル状態の量子回路を作って描画してみましょう！
# 2量子ビットの量子回路を作成
qc_1 = QuantumCircuit(2)

# アダマールゲートを作用
qc_1.h(0)

# CNOTゲートを作用
qc_1.cx(0, 1) # NOTはXと同じ意味なのでCNOTゲートを作用させるメソッドは .cx() となる

# 量子回路を図(画像)で表示
qc_1.draw("mpl")
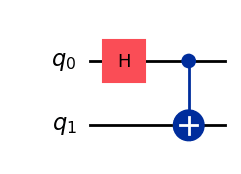
このような図が描画できました！

1つ目の量子ビットにアダマールゲートがかかり、それを制御量子ビット、2つ目の量子ビットをターゲット量子ビットとしてCNOTゲートをかけていることが分かります。

 シミュレーション量子回路を作成し、描画することが出来ました。

しかし、これだけでは本当にベル状態が作れているのかがわかりません。

状態ベクトルシミュレータを使って量子状態を確認してみましょう。
# 状態ベクトルシミュレータの実行
backend = StatevectorSimulator()
result = backend.run(qc_1).result()

# 量子状態のベクトルを出力
state_vec = result.get_statevector(qc_1)
print(state_vec)
Statevector([0.70710678+0.j, 0.        +0.j, 0.        +0.j,
             0.70710678+0.j],
            dims=(2, 2))
状態ベクトルシミュレータは、作成した量子回路が最終的にどのような量子状態になるのかを実際に計算するシミュレータです。

Qiskit Aerライブラリの StatevectorSimulator() クラスを使うことでできるようになります。

そして出力結果の1つ目の要素に、状態ベクトルが格納されています。

ベル状態のベクトル

\frac{1}{\sqrt{2}} \left(|00\rangle + |11\rangle\right) = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 0 \\ 0 \\ 1 \end{pmatrix}
と比べると、係数 \frac{1}{\sqrt{2}} \approx 0.70710678 が一致していることがわかります。
今度は「測定」まで行ってみましょう。

量子コンピュータでは、量子回路が生成する状態を途中で確認することが出来ません。

その量子回路によって状態が変化した量子ビットを繰り返し読むことで、その状態が持つ確率分布を調べることが出来ます。

これを測定と言います。
# 2量子ビットの量子回路を作成
qc_2 = QuantumCircuit(2, 2) # 2つ目の引数は古典ビット数

# ベル状態の作成
qc_2.h(0)
qc_2.cx(0, 1)

# 測定
for i in range(2):
    qc_2.measure(i, i) # measure() メソッドの引数は measure("測定する量子ビットのインデックス", "測定結果を保存する古典レジスタのインデックス") を表す

# 量子回路を図(画像)で表示
qc_2.draw("mpl")
先ほどの回路とは少し異なるのが分かります。

右側にメーターのようなアイコンのゲートが2つ出来ていると思いますが、こちらで測定を行います。

また、一番下に c とありますが、これは古典レジスタというところに古典ビットとして情報を送信しています。

この古典レジスタにあるものが量子計算の結果ということになります。
# バックエンドにシミュレータを設定
backend = AerSimulator()

# Sampler を使用しシミュレーション
sampler = SamplerV2(backend)
result = sampler.run([qc_2], shots=1024).result() # 1024回測定を行う

# 測定結果の出力
counts = result[0].data.c.get_counts()
print(counts)

# ヒストグラムを描画
plot_histogram(counts)
{'11': 531, '00': 493}
ほぼ等確率で |00\rangle と |11\rangle が測定されているのが確認出来ました！

 実機実験今度は実際の量子コンピュータを使って実験してみましょう。

まずはIBM Quantum Platformのアカウントにログインします。

そこにあるトークンをコピーして、以下のコードの QiskitRuntimeService.save_account(token="") の中に入れます。

すると自身のIBM Quantum Platformと連携出来るので、実機が使えるようになります。
# アカウント情報を連携
QiskitRuntimeService.save_account(
    channel="ibm_quantum",
    instance="ibm-q/open/main",
    token="hogehoge",
    overwrite=True
)

# 使える実機を確認
service = QiskitRuntimeService()
print(service.backends())
[<IBMBackend('ibm_brisbane')>,
 <IBMBackend('ibm_sherbrooke')>,
 <IBMBackend('ibm_kyiv')>]
上記で表示された実機をバックエンドに指定します。

各実機は、全ての量子ゲートを自在に扱えるわけではありません。

実機ごとにトポロジカルな制約があるため、それに合わせるように「翻訳」します。

よって、先ほど作った量子回路とは全く異なる形の量子回路が生成されるのですが、やっている計算そのものは同じなので安心してください。

また、馴染みのない量子ゲートも出てきますが、そこも今は理解する必要はありません。
# 実機の選択
backend = service.backend("ibm_kyiv")

# 実機が扱える量子ゲートのみで量子回路を再構築
pm = generate_preset_pass_manager(backend=backend, optimization_level=1)
isa_qc_2 = pm.run(qc_2)
isa_qc_2.draw("mpl", idle_wires=False)
それでは、実機での実験をしましょう。

IBM Quantum Platformの方でもジョブが反映されると思うので、そちらも適宜確認してください。
# Sampler でサンプリングしてジョブを作成
sampler = SamplerV2(backend)
running_job = sampler.run([isa_qc_2], shots=1024)

# ジョブのIDを取得
job_id = running_job.job_id()
print(f"Job ID:\t{job_id}")

# ジョブIDと照合
job = service.job(job_id)

# ステータスの確認
print(f"Job Status:\t{job.status()}")
QUEUED
こちら、すぐの状態だとステータスは "QUEUED" となるかと思います。

実機にジョブを投げるときに、先客がいるとキューに入った状態がしばらく続きます。

こちらが "DONE" になるまで待たなければ次のプログラムを実行することは出来ません。

ただし、上記セルを再度実行してしまうと新しいジョブを作成することになり、結局また待つことになってしまいます。

最後2行の
job = service.job(job_id)
print(f"Job Status:\t{job.status()}")
こちらだけをコピーして新しいセルで実行してステータスを確認するか、IBM Quantum Platformで実行が終わったことを確認するのが良いと思います。

もし、そのまま下記の結果確認まで同じセル内で完結させたいのであれば、 while 文と time ライブラリを駆使してステータスが "DONE" になったら次に進むというような形を取るのが良いかもしれません。
# ジョブの結果を確認
result = job.result()
counts = result[0].data.c.get_counts()
print(counts)

# ヒストグラムを描画
plot_histogram(counts)
{'11': 494, '00': 504, '01': 9, '10': 17}
結果が返ってきました！

これを見ると、ほとんどの場合 |00\rangle と |11\rangle になっているものの、少数だけ |01\rangle と |10\rangle が現れています。

これは量子コンピュータ特有のエラーによるものです。

エラーの原因はいくつかあるのですが、これらを軽減するために日々研究が行われています。

特に、今はNISQ時代と言われていて、ノイズありの中規模な量子コンピュータでしか実験が行えないため、エラーを考慮したアルゴリズムが開発されてきています。

それに対し、誤り耐性量子コンピュータ、通称FTQCの実用化もそう遠くない未来に出来ると予想されています。

今後に期待ですね！

 次回予告次回は、量子もつれを深掘りすることをテーマに進めて参ります！

GHZ状態や、あまり世間に知られていないW状態というものを扱いますので、是非また読んでみてください。