Qiskitを使った量子最適化アルゴリズムの応用へ 〜パート2 量子もつれとアルゴリズム〜

＊この記事はQiita記事の再投稿となります。

こんにちは！
株式会社アイディオットでデータサイエンティストをしています、秋田と申します。
このシリーズは、量子最適化アルゴリズムを具体的な問題に対して使うことによって、量子コンピュータのユースケースとしてどんなものがありそうかを妄想することを目的に、量子コンピュータの基礎から学ぼうというものになります。
前回は量子計算の基礎を学び、それを基にQiskitを使って量子回路を作成・実行しました。
今回は、量子もつれに焦点を当てて、特殊な量子状態を生成してみましょう！
本記事と同様の実験をGoogle Colaboratoryで簡単に出来るように、このプロジェクトのGitHubリポジトリにノートブックを作成しました。

量子もつれ

少し復習から入りましょう。
量子もつれとは、「テンソル積で表現できない状態」のことを指します。
例えば以下のベル状態

$$\frac{1}{\sqrt{2}} \left(|00\rangle + |11\rangle\right) = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 0 \\ 0 \\ 1 \end{pmatrix}$$

は典型的な量子もつれでした。
これをビット数を増やす方向に少し拡張させたGHZ状態というものと、次の

$$|W\rangle = \frac{1}{\sqrt{n}} \left(|100...0\rangle + |010...0\rangle + \cdots + |000...1\rangle\right)$$

という、 $n$ 個の量子ビットのうち1つのみを $|1\rangle$ とする $n$ 個の量子もつれの状態を表しているW状態というものを今回はマスターしましょう！
まずはQiskitの環境を整えておきましょう。

!pip3 install qiskit[visualization] qiskit-ibm-runtime qiskit-aer

# ライブラリのインポート
import numpy as np
from qiskit import __version__, QuantumCircuit
from qiskit.visualization import plot_histogram
from qiskit_aer import AerSimulator
from qiskit_ibm_runtime import SamplerV2

# Qiskitバージョン確認
print(__version__)

GHZ状態

GHZ状態は、次のような量子もつれを表します。

$$|GHZ\rangle = \frac{1}{\sqrt{2}} \left(|000...0\rangle + |111...1\rangle\right)$$

GHZ状態については、あくまでこれが一般的な表現であり、 $m$ 個目の量子ビットが反転していても同様にGHZ状態と言うことが出来ます。
ではまずは、3量子ビットのGHZ状態から作ってみましょう。

$$|GHZ\rangle = \frac{1}{\sqrt{2}} \left(|000\rangle + |111\rangle\right)$$

GHZ状態はベル状態の拡張と言いました。
考え方は同じで、アダマールゲートを1つの量子ビットにかけた後、残りの2つにCNOTゲートがかかるようにすれば大丈夫です。

# 3量子ビットの量子回路を作成
ghz_3 = QuantumCircuit(3, 3)

# GHZ状態の作成
ghz_3.h(0)
ghz_3.cx(0, 1)
ghz_3.cx(1, 2) # 1番目の量子ビットは既に0番目の量子ビットともつれているので、制御量子ビットは0, 1のどちらでも良い

# 測定
for i in range(3):
    ghz_3.measure(i, i)

# 量子回路を図(画像)で表示
ghz_3.draw("mpl")

ベル状態を作るときと同じように進めると、 $0$ 番目と $1$ 番目の量子ビットは既にエンタングル状態なので、 $2$ 番目の量子ビットをさらにもつれさせるのにどちらの量子ビットを制御量子ビットとしても構いません。
見栄えを重視すると階段状になっているのが良いかなと思いました。
さて、これで本当にGHZ状態になっているのかを測定して確かめてみましょう！

# バックエンドにシミュレータを設定
backend = AerSimulator()

# Sampler を使用しシミュレーション
sampler = SamplerV2(backend)
result = sampler.run([ghz_3], shots=1024).result() # 1024回測定を行う

# 測定結果の出力
counts = result[0].data.c.get_counts()
print(counts)

# ヒストグラムを描画
plot_histogram(counts)

{'111': 520, '000': 504}

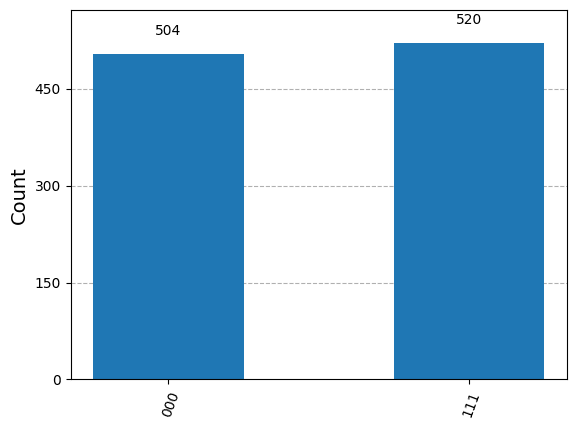
量子状態 $|000\rangle$ と $|111\rangle$ がほぼ等確率で測定されているのが確認出来ました！
それでは、今度はちょっと多くなって $8$ 量子ビットのGHZ状態を生成してみましょう。
やることは同じなので簡単ですね！

# 8量子ビットの量子回路を作成
ghz_8 = QuantumCircuit(8, 8)

# アダマールゲートを作用
ghz_8.h(0)

# 再帰的にCNOTゲートを作用
for i in range(7):
    ghz_8.cx(i, i + 1)

# バリアを使用
ghz_8.barrier()

# 測定
for i in range(8):
    ghz_8.measure(i, i)

# 量子回路を図(画像)で表示
ghz_8.draw("mpl")

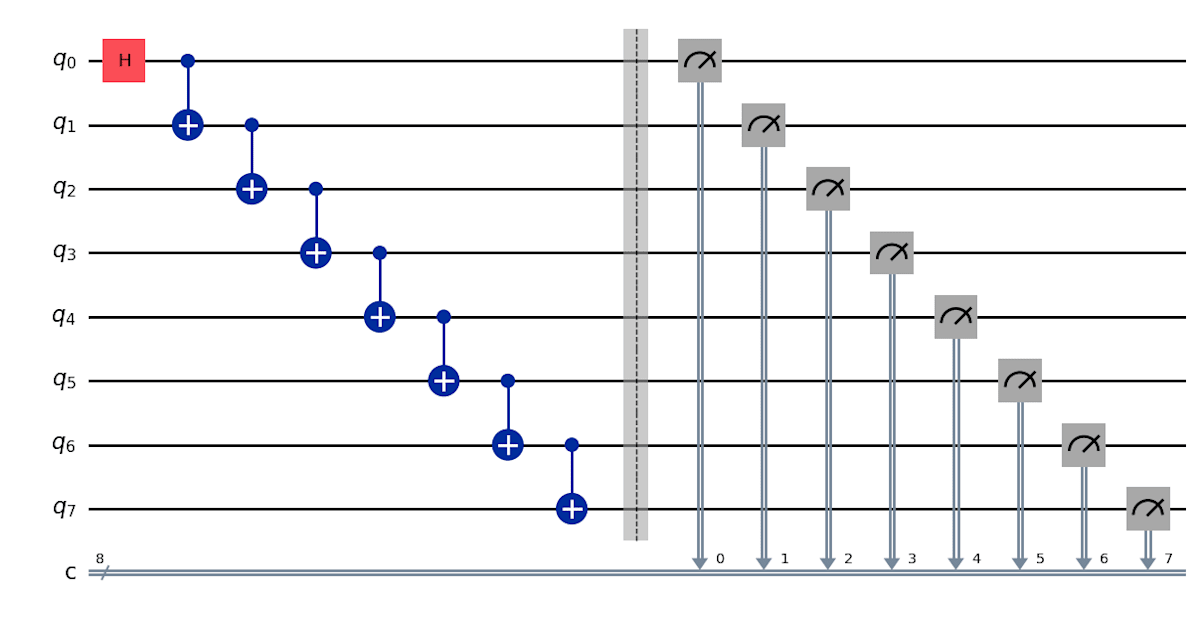
途中でバリアというものを使用していますが、これは量子回路の見栄えを良くするために書いていると理解してください。
この量子回路上で何か影響があるわけではありません。
それでは測定をして確かめてみましょう！

# バックエンドにシミュレータを設定
backend = AerSimulator()

# Sampler を使用しシミュレーション
sampler = SamplerV2(backend)
result = sampler.run([ghz_8], shots=1024).result() # 1024回測定を行う

# 測定結果の出力
counts = result[0].data.c.get_counts()
print(counts)

# ヒストグラムを描画
plot_histogram(counts)

{'11111111': 521, '00000000': 503}

$8$ 量子ビットの場合も同じように確認出来ました！
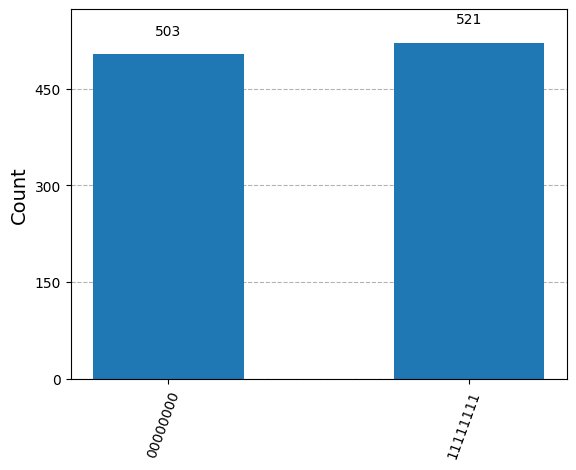
さて、ここで量子回路の「深さ」というものの考え方を導入しましょう。
先ほど作った ghz_8 の深さを depth() メソッドで確認してみましょう。

# 量子回路の深さ
print(f"Depth:\t{ghz_8.depth()}")

Depth:	9

普通、アルゴリズムを扱う上で「計算量」というものを気にします。
これは、コンピュータでの負荷を抑え、高速に計算することや、メモリを確保するためにより良いアルゴリズムを考えるというものです。
量子コンピュータでのプログラミングも例外ではなく、量子回路を設計する際にその量子回路の深さをなるべく浅く(少なく)することを心がけましょう。
例えば、 $S$ ゲートというものがあり、これを2個続けて同じ量子ビットに作用させるとそれは $Z$ ゲート1個を作用させるのと等価になります。
それであれば、 $S$ ゲートを2個続けてかけるより $Z$ ゲートを1個かけてあげる方が計算量は少なくて済むと考えられます。
より浅い回路が出来ないかを調べてみましょう！

# 8量子ビットの量子回路を作成
ghz_8_shallow = QuantumCircuit(8, 8)

# アダマールゲートを作用
ghz_8_shallow.h(0)

# CNOTゲートのかけ方を工夫
ghz_8_shallow.cx(0, 1)
ghz_8_shallow.cx(0, 2)
ghz_8_shallow.cx(1, 3)
ghz_8_shallow.cx(0, 4)
ghz_8_shallow.cx(1, 5)
ghz_8_shallow.cx(2, 6)
ghz_8_shallow.cx(3, 7)

# バリアを使用
ghz_8_shallow.barrier()

# 測定
for i in range(8):
    ghz_8_shallow.measure(i, i)

# 量子回路を図(画像)で表示
ghz_8_shallow.draw("mpl")

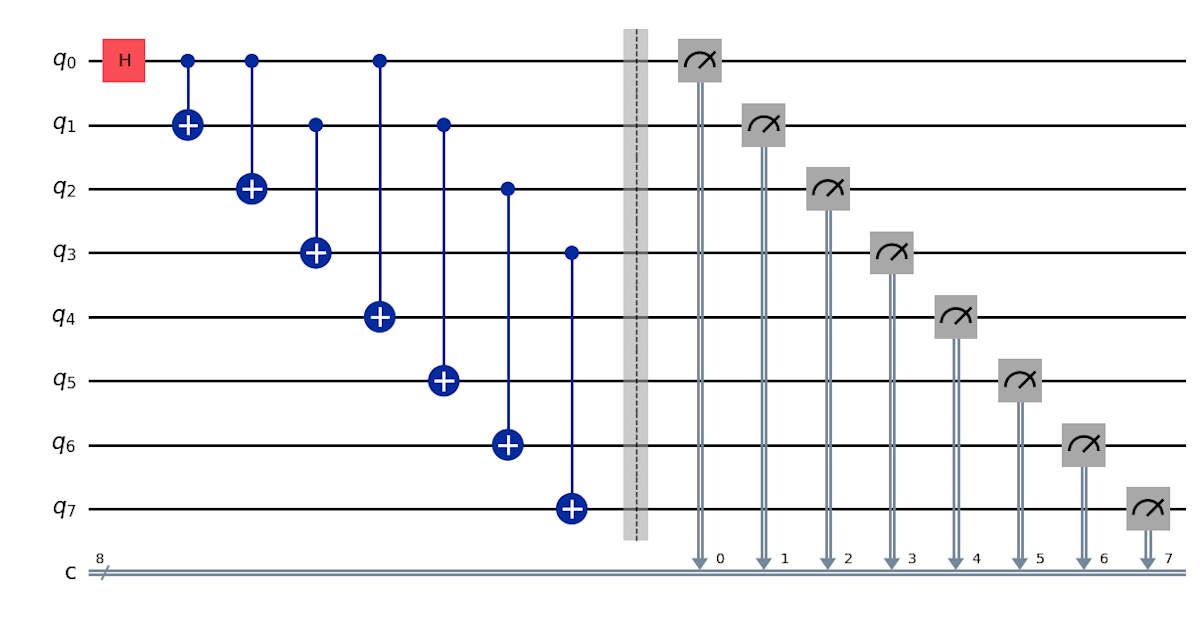
# バックエンドにシミュレータを設定
backend = AerSimulator()

# Sampler を使用しシミュレーション
sampler = SamplerV2(backend)
result = sampler.run([ghz_8_shallow], shots=1024).result() # 1024回測定を行う

# 測定結果の出力
counts = result[0].data.c.get_counts()
print(counts)

# ヒストグラムを描画
plot_histogram(counts)

{'11111111': 528, '00000000': 496}

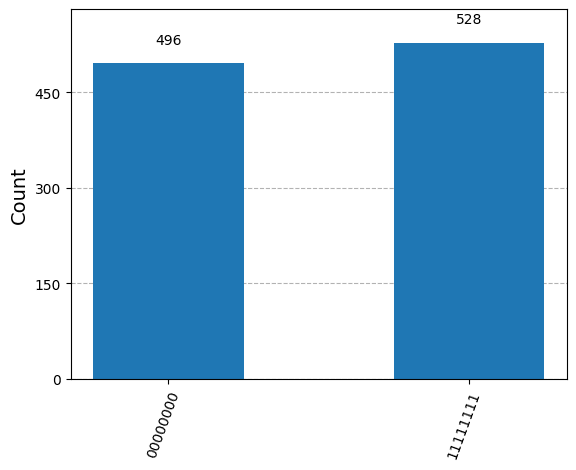
一見するとあまり変わらないように見えますが、このプログラムでは、1度もつれさせた量子ビットをなるべく満遍なく再利用することを考えています。
例えば、

ghz_8_shallow.cx(0, 4)
ghz_8_shallow.cx(1, 5)
ghz_8_shallow.cx(2, 6)
ghz_8_shallow.cx(3, 7)

ここの部分では、量子ビットのインデックス番号が1つも被っていません。
これは、それぞれのゲート作用が並行して行われていることを意味します。
一方で、先ほどの量子回路では、すべてが繋がった(線形の)ゲート作用のし方をしているため、1つ前の計算が行われてからでないと先に進めないという構造をしています。
新しい方法では、対数を用いたアルゴリズムを用いているため、線形のものより圧倒的に計算量を抑えることが出来ます！
実際に深さを確認してみましょう。

# 量子回路の深さ
print(f"Depth:\t{ghz_8_shallow.depth()}")

Depth:	5

これで浅い回路が出来たことも確認出来ました！
先ほどのプログラムだと、形が汚いので次のように関数を定めましょう。

def find_control(value: int) -> int:
    """
    制御量子ビットのインデックスを取得する関数

    Parameters
    ----------
    value: int
        ターゲット量子ビットのインデックス

    Returns
    ----------
    rem: int
        制御量子ビットのインデックス
    """
    # 2の累乗で value 以下の最大の値を求める
    power_of_two = 1 << (value.bit_length() - 1)

    # value を最大の2の累乗で割った余りを求める
    rem = value % power_of_two

    return rem

先ほどのプログラムを修正します。

# 8量子ビットの量子回路を作成
ghz_8_shallow_rec = QuantumCircuit(8, 8)

# GHZ状態の生成
ghz_8_shallow_rec.h(0)
for i in range(7):
    rem = find_control(i + 1)
    ghz_8_shallow_rec.cx(rem, i + 1)

# バリアを使用
ghz_8_shallow_rec.barrier()

# 測定
for i in range(8):
    ghz_8_shallow_rec.measure(i, i)

# 量子回路を図(画像)で表示
ghz_8_shallow_rec.draw("mpl")

だいぶスッキリしましたね！

W状態

今度は、W状態について考えてみましょう。
こちらもGHZ状態同様に、線形の作り方と対数の作り方の2種類を学びましょう。
まずは線形のやり方から始めます。
初めに、 $0$ 番目の量子ビットに $X$ ゲートをかけ、 $|100...0\rangle$ とします。
その後、次の式を満たす回転ゲートを用意します。

$$G(p) := \begin{pmatrix} \sqrt{p} & -\sqrt{1 - p} \\ \sqrt{1 - p} & \sqrt{p} \end{pmatrix}$$

ここで $p$ は $0 < p < 1$ を満たすパラメータです。
これは $R_y$ ゲートなので、 $\sqrt{p} = \cos\left(\frac{\theta'}{2}\right)$ を満たす $\theta'$ を見つけます。
実はそれほど難しくなく、 $\frac{\theta'}{2} = \arccos(\sqrt{p})$ なのですぐに見つかります(ただし、これが許容出来る近似値であることには注意が必要)。
続いて、これを使って次の変換を行うための量子ゲートのブロック $B(p)$ を定義します。

$$B(p) |00\rangle = |00\rangle, \quad B(p) |10\rangle = \sqrt{p} \space |10\rangle + \sqrt{1 - p} \space |01\rangle$$

これは、1つ目の量子ビットが $|0\rangle$ のときは2つ目の量子ビットに何もせず、1つ目の量子ビットが $|1\rangle$ のときは確率 $p$ でそのまま、確率 $1 - p$ で2つ目の量子ビットを反転させています。
1つ目の量子ビットを制御量子ビットとした $2$ 量子ビットゲートを使っていることが分かりますね！
しかし、残念ながら1つの $2$ 量子ビットゲートでは上記後半の式変換は出来ないので、2つの $2$ 量子ビットゲートを段階的にかけることで完成させましょう。
1つ目の量子ゲートは、先に定義した $G(p)$ を埋め込んだ次の $CG(p)$ ゲートを使います。

$$\begin{aligned} CG(p) &:= \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & \sqrt{p} & -\sqrt{1 - p} \\ 0 & 0 & \sqrt{1 - p} & \sqrt{p} \end{pmatrix}, \\ \\ CG(p) &: \left\{ \begin{array}{l} |00\rangle \rightarrow |00\rangle \\ |01\rangle \rightarrow |01\rangle \\ |10\rangle \rightarrow \sqrt{p} \space |10\rangle + \sqrt{1 - p} \space |11\rangle \\ |11\rangle \rightarrow \sqrt{p} \space |11\rangle - \sqrt{1 - p} \space |10\rangle \end{array} \right. \end{aligned}$$

ここで、 $|01\rangle \rightarrow |01\rangle, |11\rangle \rightarrow \sqrt{p} \space |11\rangle - \sqrt{1 - p} \space |10\rangle$ の変換は今は考える必要がありません。
次に、今度は2つ目の量子ビットを制御量子ビット、1つ目の量子ビットをターゲット量子ビットとしたCNOTゲートを作用させることで、

$$\sqrt{p} \space |10\rangle + \sqrt{1 - p} \space |11\rangle \rightarrow \sqrt{p} \space |10\rangle + \sqrt{1 - p} \space |01\rangle$$

となります。
よって先ほどの量子ゲート $B(p)$ は、

$$B(p) = \text{CNOT}_{1, 0} \space CG(p)_{0, 1}$$

として表せます。
この $B(p)$ を階段状に順番にかけていくことでW状態は出来るので、例として $4$ 量子ビットのW状態を作ってみましょう！
まずは以下の初期状態 $| \Psi_0 \rangle$ を用意します。

$$| \Psi_0 \rangle = |0000\rangle$$

ここから、1つ目の量子ビットに $X$ ゲートをかけて

$$| \Psi_1 \rangle = |1000\rangle$$

とします。
理想とするW状態は

$$|W\rangle = \sqrt{\frac{1}{4}} \space |1000\rangle + \sqrt{\frac{1}{4}} \space |0100\rangle + \sqrt{\frac{1}{4}} \space |0010\rangle + \sqrt{\frac{1}{4}} \space |0001\rangle$$

なので、 $|1000\rangle$ の係数としては $\sqrt{\frac{1}{4}}$ を残したいですね。
よってここでは $p = \frac{1}{4}$ とし、

$$| \Psi_2 \rangle = B \left( \frac{1}{4} \right) |10\rangle \otimes |00\rangle = \sqrt{\frac{1}{4}} \space |1000\rangle + \sqrt{\frac{3}{4}} \space |0100\rangle$$

とします。
続いて、 $|0100\rangle$ の係数を $\sqrt{\frac{1}{4}}$ にするために $p = \frac{1}{3}$ とし、

$$\begin{aligned} | \Psi_3 \rangle &= \sqrt{\frac{1}{4}} \left( |1\rangle \otimes B \left( \frac{1}{3} \right) |00\rangle \otimes |0\rangle \right) + \sqrt{\frac{3}{4}} \left( |0\rangle \otimes B \left( \frac{1}{3} \right) |10\rangle \otimes |0\rangle \right) \\ &= \sqrt{\frac{1}{4}} \space |1000\rangle + \sqrt{\frac{3}{4} \frac{1}{3}} \space |0100\rangle + \sqrt{\frac{3}{4} \frac{2}{3}} \space |0010\rangle \end{aligned}$$

とします。
最後に $|0010\rangle$ の係数を $\sqrt{\frac{1}{4}}$ にするために $p = \frac{1}{2}$ とすると、

$$\begin{aligned} | \Psi_4 \rangle &= \sqrt{\frac{1}{4}} \left( |10\rangle \otimes B \left( \frac{1}{2} \right) |00\rangle \right) + \sqrt{\frac{3}{4} \frac{1}{3}} \left( |01\rangle \otimes B \left( \frac{1}{2} \right) |00\rangle \right) + \sqrt{\frac{3}{4} \frac{2}{3}} \left( |00\rangle \otimes B \left( \frac{1}{2} \right) |10\rangle \right)\\ &= \sqrt{\frac{1}{4}} \space |1000\rangle + \sqrt{\frac{3}{4} \frac{1}{3}} \space |0100\rangle + \sqrt{\frac{3}{4} \frac{2}{3} \frac{1}{2}} \space |0010\rangle + \sqrt{\frac{3}{4} \frac{2}{3} \frac{1}{2}} \space |0001\rangle \\ &= |W\rangle \end{aligned}$$

となりました！

# 量子ビット数を指定
n = 4

# W状態のエンタングルメントの係数
prob_amp = np.sqrt(1 / n)

# n量子ビットの量子回路を作成
w_n = QuantumCircuit(n, n)

# W状態の作成
w_n.x(0)
for i in range(n - 1):
    comp_amp = np.sqrt(1 - i / n)
    rot_ang = 2 * np.arccos(prob_amp / (comp_amp)) # 回転角の大きさを係数から判定
    w_n.cry(rot_ang, i, i + 1) # cryゲートがCG(p)に相当する
    w_n.cx(i + 1, i)

# バリアを使用
w_n.barrier()

# 測定
for i in range(n):
    w_n.measure(i, i)

# 量子回路を図(画像)で表示
w_n.draw("mpl")

# バックエンドにシミュレータを設定
backend = AerSimulator()

# Sampler を使用しシミュレーション
sampler = SamplerV2(backend)
result = sampler.run([w_n], shots=1024).result() # 1024回測定を行う

# 測定結果の出力
counts = result[0].data.c.get_counts()
print(counts)

# ヒストグラムを描画
plot_histogram(counts)

{'0001': 253, '0100': 248, '1000': 268, '0010': 255}

W状態が確認出来ました！
では、この量子回路の深さを確認しましょう。
比較がしやすいように量子ビット数を $8$ に固定したものを再度実行します。

# W状態のエンタングルメントの係数
prob_amp = np.sqrt(1 / 8)

# 8量子ビットの量子回路を作成
w_8 = QuantumCircuit(8, 8)

# W状態の作成
w_8.x(0)
for i in range(7):
    comp_amp = np.sqrt(1 - i / 8)
    rot_ang = 2 * np.arccos(prob_amp / (comp_amp)) # 回転角の大きさを係数から判定
    w_8.cry(rot_ang, i, i + 1) # cryゲートがCG(p)に相当する
    w_8.cx(i + 1, i)

# バリアを使用
w_8.barrier()

# 測定
for i in range(8):
    w_8.measure(i, i)

# 量子回路を図(画像)で表示
w_8.draw("mpl")

# 量子回路の深さ
print(f"Depth:\t{w_8.depth()}")

Depth:	16

GHZ状態のときと同様に、より浅い量子回路を作成するために対数を用いた作り方を考えてみましょう。
こちらは少しトリッキーなので順を追って見ていきましょう。
まず、対数を用いたアルゴリズムなので、W状態の量子回路の深さというのは量子ビット数 $n$ に対し $2 \lceil \log_2 n \rceil + 2$ で求まります。
最後の $+2$ は、最初の $X$ ゲートと測定によるものなので、実質考えるべきなのは $\lceil \log_2 n \rceil$ の部分となります。
また、 $2$ を最初にかけているのは $CR_y$ ゲートとCNOTゲートの2種類をかけているためで、ブロックとしては $\lceil \log_2 n \rceil$ 個になるはずです。
そして、先ほどまでのように線形で係数の変遷を追っていけないので、それを管理するための要素数 $n$ の仮のリストを持っておきましょう。
このリストは合計が $n$ になるようにして、最終的に全て $1$ になれば係数が管理できることになります。
あとは $\lceil \log_2 n \rceil$ 回のforループの中で係数リストを更新しながらW状態を作ります。

# 8量子ビットの量子回路を作成
w_8_shallow = QuantumCircuit(8, 8)

# 対数を取った値
levels = int(np.ceil(np.log2(8)))

# 係数を管理するリスト
box = [0 for _ in range(8)]
box[0] = 8

# W状態の作成
w_8_shallow.x(0)
for level in range(levels):
    tmp = 2**level
    for i in range(tmp):
        parent = box[i]
        if parent == 1:
            continue

        left = parent//2
        right = parent - left

        prob_amp = np.sqrt(left / parent)
        rot_ang = 2 * np.arccos(prob_amp)

        for j in range(tmp, 8):
            if box[j] == 0:
                bridge = j
                break

        w_8_shallow.cry(rot_ang, i, bridge)
        w_8_shallow.cx(bridge, i)

        box[i] = left
        box[bridge] = right

# バリアを使用
w_8_shallow.barrier()

# 測定
for i in range(8):
    w_8_shallow.measure(i, i)

# 量子回路を図(画像)で表示
w_8_shallow.draw("mpl")

# 量子回路の深さ
print(f"Depth:\t{w_8_shallow.depth()}")

Depth:	8

だいぶ浅くなりましたね！

次回予告

次回は、変分量子アルゴリズムとはどういうものかを知ることをテーマに進めて参ります！
実際に、量子化学や量子最適化、量子機械学習などで扱われているアルゴリズムがどのようなものなのかを紹介しますので、是非また読んでみてください。