相関と因果は混ぜるな危険 PCアルゴリズムを用いたe-learningのデータの因果推論
※弊社の教材はe-learningではなく、オンラインDXラーニングと呼びます。弊社のコンテンツを分析したわけではないのでこのタイトルで許してください。

相関関係は因果関係を示したものではないと統計学で習い、じゃあ因果関係を示す手法を教えてくれよって頭が爆発しそうになった皆さんこんにちは。自分は何回も爆発しました。
本記事はe-learningのデータセットとPCアルゴリズムを用いてどの要素がどのように関係していくのか調べました。
前回までのあらすじ 相関関係と因果関係をごっちゃにしてはいけない

一年前に書いた記事より

一年前の宣言を忘れずにSQL力を少し身に着け、いろいろなデータを見てきました。
しかし、データは抜き出せたものの、SQLがわからない人たちにどう説明すればよいのか困るデータがたくさん出てきました。
例えば弊社ではコンテンツのリニューアルを行っており、おおよそリニューアルコースは評価は良くなります。
しかし
- 序盤は良い評価が多い
- 暫く経つと評価が下がる
と時間経過で評価が下がるような現象が起きたり(数ヶ月のスパンなので鮮度が落ちたとは考えられない)、
リニューアル後評価が上がったけど
- コースとターゲット層がマッチしたから?
- 動画の本数が増えたから?(たしかにリニューアルコースに限った話だと動画の本数と評価に一定の相関はある)
- 解説がわかりやすくなったから?
- 活用イメージが湧くようになったから?
...などデータごとの相関はあるものの、何が原因で良くなったのかがわからないからノウハウが蓄積できないなど、データ活用の面でも非常に困りました。
今回は事象の因果を読み解くべく、e-learningのデータを用いて、各要素がどのような因果関係があるのか調べました。
因果の定義
ここでの因果関係の定義は
ある変数xを増やしたとき、対応する変数yが増える状況
とします。
例えば身長をxとして体重をyをした場合xとyには相関関係はあります。
しかし身長が増えたらその人の体重は増えますが、体重が増えたから身長が伸びるとは言えないのでx→yに因果関係はあるけどy→xに因果関係はないと言えます。
使うデータセット
データセットは以下の物を使います。
概要
データセットはブラジルの大学での4ヶ月間のアルゴリズム入門クラス後に収集。
学生のパフォーマンスは従来の評価システムを使用して評価され、同時にオンライン環境では学生が投稿を共有し、絵文字ベースの反応で作品を分類しました。
上記サイトを参考に投稿の例を作ると
pythonでHelloと出力するにはどうしたらいいか?
print("Hello)
☆4
🤝3
のように投稿と他の学生からのリアクションのような形でオンラインでやりとりをしていたと推測されます。
授業はプロジェクトベースであり、スキルの評価は「21世紀のスキル」として0から10のスケールで教員が評価したそうです。評価対象のスキルには以下が含まれます:
批判的思考と問題解決スキル(SK1)
創造性とイノベーションスキル(SK2)
自己学習スキル(SK3)
コラボレーションと自己指導スキル(SK4)
社会的および文化的責任(SK5)
オンライン学習環境では、学生は投稿を行い、同じクラスの投稿に以下の反応を付けられました。
「混乱させる投稿」
「素晴らしい投稿」
「悪い投稿」
「創造的な投稿」
「協力的な投稿」
「素晴らしいコードの投稿」
「役立つ投稿」
データセットの最後の列には、学生がクラスに合格したかどうかが示されています。最終結果は5つのスキルの平均でした。
データセットの各項目は以下の通り。
Unnamed: 0: おそらく行番号またはID。
total_posts: 投稿の総数。
helpful_post: 役立つ投稿の数。
nice_code_post: 素晴らしいコードの投稿数。
collaborative_post: 協力的な投稿の数。
confused_post: 混乱させる投稿の数。
creative_post: 創造的な投稿の数。
bad_post: 悪い投稿の数。
amazing_post: 素晴らしい投稿の数。
timeonline: オンラインで過ごした時間(単位は秒)。
sk1_classroom 〜 sk5_classroom: 5つのスキル(批判的思考・問題解決、創造性・イノベーション、自己学習、コラボレーション・自己指導、社会的・文化的責任)に関するクラス内の評価。
Approved: クラスに合格したかどうか(1は合格、0は不合格)。
今回用いるPCアルゴリズムと流れ
今回用いるものはPCアルゴリズム(Peter-Clarkアルゴリズム)と呼ばれるアルゴリズムを使います。統計的データから因果関係を推論するための方法の一つで、特に観測データから変数間の因果ネットワークを構築するのに用いられます。
このアルゴリズの流れは以下のとおりです。
前処理(モデルが処理できる形にする)
→
カイ二乗検定を用いた独立性の検定をし関係図(スケルトンと呼ばれます。)を作成(関連がある要素のつながりを特定する)
→
グラフの向きの特定し、因果関係を特定(特定したものはDAGと呼ばれます。)
→
関連性の考察
前処理(モデルが処理できる形にする)
では順にデータを処理していきます。
まずは大まかにデータの特徴を把握していきます。
import pandas as pd
from ydata_profiling import ProfileReport
df = pd.read_csv("data\online_classroom_data.csv")
profile = ProfileReport(df, title="Profiling Report")
profile
出力結果(一部)
欠損値はなし。

Unnamed: 0: おそらく行番号またはID。
は使わないので削除します。
5つのスキルに関するクラス内の評価はカテゴリカル変数として格納されているので数値に変換します。
import pandas as pd
df = pd.read_csv("data\online_classroom_data.csv")
# 0行目を削除
data_cleaned = df.drop(columns=['Unnamed: 0'])
# カテゴリカル変数を数値に変換
skill_columns = ['sk1_classroom', 'sk2_classroom', 'sk3_classroom', 'sk4_classroom', 'sk5_classroom']
for col in skill_columns:
data_cleaned[col] = data_cleaned[col].str.replace(',', '.').astype(float)
data_cleaned.info()
出力結果は以下のとおりです。
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 71 entries, 0 to 70
Data columns (total 15 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 total_posts 71 non-null float64
1 helpful_post 71 non-null float64
2 nice_code_post 71 non-null float64
3 collaborative_post 71 non-null float64
4 confused_post 71 non-null float64
5 creative_post 71 non-null float64
6 bad_post 71 non-null float64
7 amazing_post 71 non-null float64
8 timeonline 71 non-null float64
9 sk1_classroom 71 non-null float64
10 sk2_classroom 71 non-null float64
11 sk5_classroom 71 non-null float64
12 sk3_classroom 71 non-null float64
13 sk4_classroom 71 non-null float64
14 Approved 71 non-null int64
dtypes: float64(14), int64(1)
memory usage: 8.4 KB
数値に変換できました。
相関関係の確認
ydata_profilingで出せるのですが見にくかったので一旦コードを書き直しました。
correlation_matrix = data_cleaned.corr()
plt.figure(figsize=(12, 8))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', fmt=".2f")
plt.title("Correlation Matrix of All Variables")
plt.show()
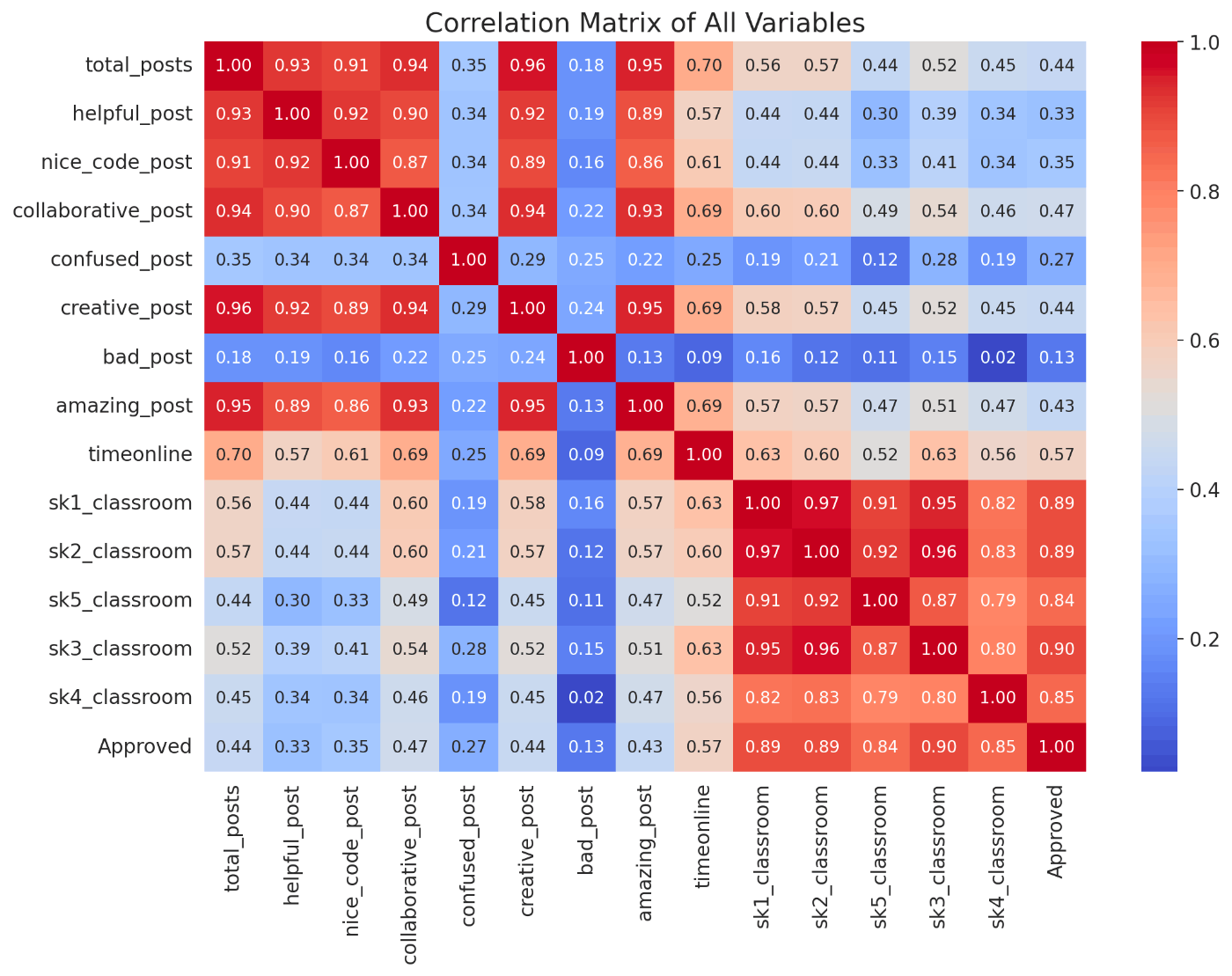
上記から以下が読み取れます。
- なにかしらの良い反応をされる人は他の良い反応をされる。
- スキル値の高さと合格には相関性がある。
- 各スキル値ごとに相関がある。
反応の合計値をまとめた値を整数値にする
今回は良い反応と悪い反応の合計値をそれぞれgood_reactionとbad_reaction、各スキル値の平均をavg_skillにまとめ、さらにカイ二乗検定をするために整数値に直します。
good_columns = ['helpful_post', 'nice_code_post', 'collaborative_post', 'creative_post', 'amazing_post']
data_cleaned['good_reaction'] = data_cleaned[good_columns].sum(axis=1)
# 'bad_reaction' 列を作成し、指定された列の合計を計算する
bad_columns = ['confused_post', 'bad_post']
data_cleaned['bad_reaction'] = data_cleaned[bad_columns].sum(axis=1)
# Avg skillを作成
avg_skill = ['sk1_classroom', 'sk2_classroom', 'sk3_classroom', 'sk4_classroom', 'sk5_classroom']
data_cleaned['avg_skill'] = data_cleaned[avg_skill].mean(axis=1)
# 必要な列を選択して新しいDataFrameを作成
selected_columns = ['total_posts', 'good_reaction', 'bad_reaction','timeonline', 'avg_skill','Approved']
data_cleaned_add_reaction = data_cleaned[selected_columns]
# 整数にする
data_cleaned_add_reaction['avg_skill'] = data_cleaned_add_reaction['avg_skill'].astype(int)
# 結果を確認する
print(data_cleaned_add_reaction.head())
出力結果
total_posts good_reaction bad_reaction timeonline avg_skill Approved
0 1.0 7.0 0.0 1600.0 2 0
1 1.0 6.0 0.0 592.0 0 0
2 2.0 40.0 1.0 1110.0 6 1
3 5.0 32.0 2.0 8651.0 5 1
4 14.0 144.0 0.0 34172.0 8 1
カイ二乗検定を用いた独立性の検定をし、関係図作成(関連がある要素のつながりを特定する)
カラムの独立性を確認していきます。
0次の独立性の確認
まずは各カラムごとの独立性を確認します。
from pgmpy.estimators.CITests import chi_square
from itertools import combinations
from pgmpy.estimators.CITests import chi_square
# あなたのデータフレーム
# data_cleaned_add_reaction = pd.read_csv('your_file.csv') # データフレームの読み込み
# データフレームのカラム名
columns = ['total_posts', 'good_reaction', 'bad_reaction', 'timeonline', 'avg_skill','Approved']
# カラムのすべての組み合わせを生成
column_combinations = list(combinations(columns, 2))
# カイ二乗検定の結果を格納するリスト
chi_square_results = []
# すべての組み合わせに対してカイ二乗検定を実行
for combo in column_combinations:
X, Y = combo
result = chi_square(X=X, Y=Y, Z=[], data=data_cleaned_add_reaction, boolean=True, significance_level=0.05)
chi_square_results.append((X, Y, result))
# 結果を表示
for result in chi_square_results:
print(f"カラム {result[0]} と {result[1]} の間のカイ二乗検定結果: {result[2]}")
出力結果
カラム total_posts と good_reaction の間のカイ二乗検定結果: False
カラム total_posts と bad_reaction の間のカイ二乗検定結果: False
カラム total_posts と timeonline の間のカイ二乗検定結果: False
カラム total_posts と avg_skill の間のカイ二乗検定結果: False
カラム total_posts と Approved の間のカイ二乗検定結果: False
カラム good_reaction と bad_reaction の間のカイ二乗検定結果: False
カラム good_reaction と timeonline の間のカイ二乗検定結果: False
カラム good_reaction と avg_skill の間のカイ二乗検定結果: False
カラム good_reaction と Approved の間のカイ二乗検定結果: True
カラム bad_reaction と timeonline の間のカイ二乗検定結果: False
カラム bad_reaction と avg_skill の間のカイ二乗検定結果: True
カラム bad_reaction と Approved の間のカイ二乗検定結果: True
カラム timeonline と avg_skill の間のカイ二乗検定結果: False
カラム timeonline と Approved の間のカイ二乗検定結果: True
カラム avg_skill と Approved の間のカイ二乗検定結果: False
以下のカラムで0次の独立性が確認できました。
カラム good_reaction と Approved の間のカイ二乗検定結果: True
カラム bad_reaction と avg_skill の間のカイ二乗検定結果: True
カラム bad_reaction と Approved の間のカイ二乗検定結果: True
カラム timeonline と Approved の間のカイ二乗検定結果: True
図にするとこう

上の描画のコードは以下の通り
import daft
from daft import PGM
import matplotlib.pyplot as plt
%matplotlib inline
pgm = PGM(shape=[6, 6]) # 幅と高さをさらに大きくしています
# ノード(変数)の追加(ノードの座標を2倍にして間隔を広げています)
nodes = ["total_posts", "good_reaction", "bad_reaction", "timeonline", "avg_skill", "Approved"]
positions = [(0, 4), (2, 4), (1, 6), (0, 2), (2, 2), (4, 2)]
scale = 2 # ノードの大きさ
for node, pos in zip(nodes, positions):
pgm.add_node(daft.Node(node, node, *pos, scale=scale))
# エッジ(関係)の追加
# 独立性が否定された変数間にエッジを追加
pgm.add_edge("total_posts", "good_reaction",directed=False)
pgm.add_edge("total_posts", "bad_reaction",directed=False)
pgm.add_edge("total_posts", "timeonline",directed=False)
pgm.add_edge("total_posts", "avg_skill",directed=False)
pgm.add_edge("total_posts", "Approved",directed=False)
pgm.add_edge("good_reaction", "bad_reaction",directed=False)
pgm.add_edge("good_reaction", "timeonline",directed=False)
pgm.add_edge("good_reaction", "avg_skill",directed=False)
pgm.add_edge("bad_reaction", "timeonline",directed=False)
pgm.add_edge("timeonline", "avg_skill",directed=False)
pgm.add_edge("avg_skill", "Approved",directed=False)
# DAGの描画
pgm.render()
plt.show()
一次の独立性の確認
次に一次の独立性をチェックします。
0次の独立性との違いは
- 0次の独立性:2つの事柄が互いに関係していないか確認
- 1次の独立性:2つの事柄が互いに関係していないかを、別の事柄(条件)を加えて確認
例えば0次なら朝ごはんの量と、学校でのテストの成績が0次の独立性を持っているとしたら、どれだけ朝ごはんを食べてもテストの成績には影響しないと判断できます。
1次の独立性なら「朝ごはんの量」と「夜の睡眠時間」が1次の独立性を持っているかどうかを考えるとき、「学校でのテストの成績」という別の条件を考慮します。この場合、朝ごはんの量と夜の睡眠時間がテストの成績によってどのように変わるかを見ます。
from itertools import permutations
# データフレームの全カラム
all_columns = ['good_reaction', 'bad_reaction', 'timeonline', 'avg_skill', 'Approved']
# 除外するカラムペア
excluded_pairs = [
('good_reaction', 'Approved'),
('bad_reaction', 'avg_skill'),
('bad_reaction', 'Approved'),
('timeonline', 'Approved')
]
# 除外されたペアに関連する条件変数を生成
excluded_conditions = {x: set() for x in all_columns}
for x, y in excluded_pairs:
excluded_conditions[x].add(y)
excluded_conditions[y].add(x)
# 一次の独立性をチェックするための結果リスト
first_order_independence_results = []
# 全てのカラムペアに対して、他の全カラムを条件としてカイ二乗検定を実行(特定のペアとその関連要素を除外)
for x, y in permutations(all_columns, 2):
if (x, y) not in excluded_pairs and (y, x) not in excluded_pairs:
for z in all_columns:
if z != x and z != y and z not in excluded_conditions[x] and z not in excluded_conditions[y]:
result = chi_square(X=x, Y=y, Z=[z], data=data_cleaned_add_reaction, boolean=True, significance_level=0.05)
first_order_independence_results.append((x, y, z, result))
# 結果を表示
first_order_independence_results
出力結果
[('total_posts', 'good_reaction', 'bad_reaction', False),
('total_posts', 'good_reaction', 'timeonline', False),
('total_posts', 'good_reaction', 'avg_skill', False),
('total_posts', 'bad_reaction', 'good_reaction', True),
('total_posts', 'bad_reaction', 'timeonline', False),
('total_posts', 'timeonline', 'good_reaction', True),
('total_posts', 'timeonline', 'bad_reaction', False),
('total_posts', 'timeonline', 'avg_skill', False),
('total_posts', 'avg_skill', 'good_reaction', True),
('total_posts', 'avg_skill', 'timeonline', False),
('total_posts', 'avg_skill', 'Approved', False),
('total_posts', 'Approved', 'avg_skill', False),
('good_reaction', 'total_posts', 'bad_reaction', False),
('good_reaction', 'total_posts', 'timeonline', False),
('good_reaction', 'total_posts', 'avg_skill', False),
('good_reaction', 'bad_reaction', 'total_posts', True),
('good_reaction', 'bad_reaction', 'timeonline', False),
('good_reaction', 'timeonline', 'total_posts', True),
('good_reaction', 'timeonline', 'bad_reaction', False),
('good_reaction', 'timeonline', 'avg_skill', False),
('good_reaction', 'avg_skill', 'total_posts', True),
('good_reaction', 'avg_skill', 'timeonline', False),
('bad_reaction', 'total_posts', 'good_reaction', True),
('bad_reaction', 'total_posts', 'timeonline', False),
('bad_reaction', 'good_reaction', 'total_posts', True),
('bad_reaction', 'good_reaction', 'timeonline', False),
('bad_reaction', 'timeonline', 'total_posts', True),
('bad_reaction', 'timeonline', 'good_reaction', True),
('timeonline', 'total_posts', 'good_reaction', True),
('timeonline', 'total_posts', 'bad_reaction', False),
('timeonline', 'total_posts', 'avg_skill', False),
('timeonline', 'good_reaction', 'total_posts', True),
('timeonline', 'good_reaction', 'bad_reaction', False),
('timeonline', 'good_reaction', 'avg_skill', False),
('timeonline', 'bad_reaction', 'total_posts', True),
('timeonline', 'bad_reaction', 'good_reaction', True),
('timeonline', 'avg_skill', 'total_posts', True),
('timeonline', 'avg_skill', 'good_reaction', True),
('avg_skill', 'total_posts', 'good_reaction', True),
('avg_skill', 'total_posts', 'timeonline', False),
('avg_skill', 'total_posts', 'Approved', False),
('avg_skill', 'good_reaction', 'total_posts', True),
('avg_skill', 'good_reaction', 'timeonline', False),
('avg_skill', 'timeonline', 'total_posts', True),
('avg_skill', 'timeonline', 'good_reaction', True),
('avg_skill', 'Approved', 'total_posts', False),
('Approved', 'total_posts', 'avg_skill', False),
('Approved', 'avg_skill', 'total_posts', False)]
以下のカラムで一次の独立を確認できました。
('total_posts', 'bad_reaction', 'good_reaction', True)
('total_posts', 'timeonline', 'good_reaction', True)
('total_posts', 'avg_skill', 'good_reaction', True)
('good_reaction', 'bad_reaction', 'total_posts', True)
('good_reaction', 'timeonline', 'total_posts', True)
('good_reaction', 'avg_skill', 'total_posts', True)
('bad_reaction', 'total_posts', 'good_reaction', True)
('bad_reaction', 'good_reaction', 'total_posts', True)
('bad_reaction', 'timeonline', 'total_posts', True)
('bad_reaction', 'timeonline', 'good_reaction', True)
('timeonline', 'total_posts', 'good_reaction', True)
('timeonline', 'bad_reaction', 'total_posts', True)
('timeonline', 'bad_reaction', 'good_reaction', True)
('timeonline', 'avg_skill', 'total_posts', True)
('timeonline', 'avg_skill', 'good_reaction', True)
('avg_skill', 'total_posts', 'good_reaction', True)
('avg_skill', 'good_reaction', 'total_posts', True)
('avg_skill', 'timeonline', 'total_posts', True)
('avg_skill', 'timeonline', 'good_reaction', True)
しかし、これだけでは独立性を確認できず、ノードを削除できません。
例えば
('bad_reaction', 'good_reaction', 'total_posts', True)
に注目したとき(赤枠が条件、赤線がつながり)、他のノード(timeonline)も考慮できていないのでここでは互いに独立とは言えません。

二、三次の独立性の確認
そこで二次、三次の独立の確認をします。
1次なら「朝ごはんの量」と「夜の睡眠時間」が1次の独立性を持っているかどうかを考えるとき、「学校でのテストの成績」という別の条件を考慮しましたが、二次では「課外活動での運動時間」の条件を追加で考慮します。
from itertools import permutations
# 一次の独立性がFalseであった結果
first_order_results = [
('total_posts', 'good_reaction', 'bad_reaction', False),
('total_posts', 'good_reaction', 'timeonline', False),
('total_posts', 'good_reaction', 'avg_skill', False),
('total_posts', 'bad_reaction', 'timeonline', False),
('total_posts', 'timeonline', 'bad_reaction', False),
('total_posts', 'timeonline', 'avg_skill', False)
,('total_posts', 'avg_skill', 'timeonline', False),
('total_posts', 'avg_skill', 'Approved', False),
('total_posts', 'Approved', 'avg_skill', False),
('good_reaction', 'total_posts', 'bad_reaction', False),
('good_reaction', 'total_posts', 'timeonline', False),
('good_reaction', 'total_posts', 'avg_skill', False),
('good_reaction', 'bad_reaction', 'timeonline', False),
('good_reaction', 'timeonline', 'bad_reaction', False),
('good_reaction', 'timeonline', 'avg_skill', False),
('good_reaction', 'avg_skill', 'timeonline', False),
('bad_reaction', 'total_posts', 'timeonline', False),
('bad_reaction', 'good_reaction', 'timeonline', False),
('timeonline', 'total_posts', 'bad_reaction', False),
('timeonline', 'total_posts', 'avg_skill', False),
('timeonline', 'good_reaction', 'bad_reaction', False),
('timeonline', 'good_reaction', 'avg_skill', False),
('timeonline', 'bad_reaction', 'good_reaction', False),
('avg_skill', 'total_posts', 'timeonline', False),
('avg_skill', 'total_posts', 'Approved', False),
('avg_skill', 'good_reaction', 'timeonline', False),
('avg_skill', 'Approved', 'total_posts', False),
('Approved', 'total_posts', 'avg_skill', False),
('Approved', 'avg_skill', 'total_posts', False)
]
# データフレームの全カラム
all_columns = ["total_posts", "good_reaction", "bad_reaction", "timeonline", "avg_skill", "Approved"]
# 二次の独立性をチェックするための結果リスト
second_order_independence_results = []
# 一次の独立性がFalseであった各ペアに対して、他の全カラムを条件としてカイ二乗検定を実行
for x, y, z, independence in first_order_results:
if not independence: # 一次の独立性がFalseであるペアに対してのみ実行
for w in all_columns:
if w not in [x, y, z]:
# 二次の独立性をチェック
result = chi_square(X=x, Y=y, Z=[z, w], data=data_cleaned_add_reaction, boolean=True, significance_level=0.05)
second_order_independence_results.append((x, y, z, w, result))
# 結果を表示
second_order_independence_results
出力結果は長いのでTrueのものだけ抽出すると
('total_posts', 'timeonline', 'bad_reaction', 'good_reaction', True),
('total_posts', 'timeonline', 'avg_skill', 'good_reaction', True),
('total_posts', 'avg_skill', 'Approved', 'good_reaction', True),
('timeonline', 'total_posts', 'bad_reaction', 'good_reaction', True),
('timeonline', 'total_posts', 'avg_skill', 'good_reaction', True),
('timeonline', 'bad_reaction', 'good_reaction', 'avg_skill', True),
('timeonline', 'bad_reaction', 'good_reaction', 'Approved', True),
('avg_skill', 'total_posts', 'Approved', 'good_reaction', True),
('avg_skill', 'Approved', 'total_posts', 'good_reaction', True),
('Approved', 'avg_skill', 'total_posts', 'good_reaction', True)
となりました。
三次も同様にして(コード略)
[('total_posts', 'timeonline', 'bad_reaction', 'Approved', 'good_reaction', True),
('total_posts', 'timeonline', 'avg_skill', 'Approved', 'good_reaction', True),
('total_posts', 'avg_skill', 'Approved', 'bad_reaction', 'good_reaction', True),
('good_reaction', 'timeonline', 'bad_reaction', 'avg_skill', 'total_posts', True),
('good_reaction', 'timeonline', 'avg_skill', 'bad_reaction', 'total_posts', True),
('good_reaction', 'timeonline', 'avg_skill', 'Approved', 'total_posts', True),
('timeonline', 'total_posts', 'bad_reaction', 'Approved', 'good_reaction', True),
('timeonline', 'total_posts', 'avg_skill', 'Approved', 'good_reaction', True),
('timeonline', 'good_reaction', 'bad_reaction', 'avg_skill', 'total_posts', True),
('timeonline', 'good_reaction', 'avg_skill', 'bad_reaction', 'total_posts', True),
('timeonline', 'good_reaction', 'avg_skill', 'Approved', 'total_posts', True),
('avg_skill', 'total_posts', 'Approved', 'bad_reaction', 'good_reaction', True),
('avg_skill', 'Approved', 'total_posts', 'bad_reaction', 'good_reaction', True),
('Approved', 'avg_skill', 'total_posts', 'bad_reaction', 'good_reaction', True)]
となりました。以上を考慮すると

赤の点線の箇所が消せます。
因果の方向づけ
これまでの検定で以下の関係性が確認できました。
オリエンテーションルールによる方向づけ
部分的に因果の方向を求めていき、全体の因果を求めていきます。
ここではV字構造になっている箇所について方向の推定をしていきます。

推定を行う箇所
print(chi_square(X='bad_reaction', Y='Approved', Z=['total_posts'], data=data_cleaned_add_reaction, boolean=True, significance_level=0.05))
print(chi_square(X='bad_reaction', Y='avg_skill', Z=['good_reaction'], data=data_cleaned_add_reaction, boolean=True, significance_level=0.05))
print(chi_square(X='bad_reaction', Y='avg_skill', Z=['timeonline'], data=data_cleaned_add_reaction, boolean=True, significance_level=0.05))
出力結果
True
True
False
timeonlineを条件にしたbad_reactionとavg_skillだけFalseになりました。
つまりbad_reactionとavg_skillはtimeonlineをもとに独立していないと判断できるので以下のように方向づけが出来ます。
時間順序による方向づけ
オリエンテーションルールでは三変数の方向しかわかりませんでしたが、ここからは時間的順序を考慮してつけていきます。
例えば
total_postとApproveなら投稿数が多いと合格しやすい(合格すると投稿数が増えるとは考えられない)
のように判断していきます。判断した結果は以下の通り。
total_postとgood_reaction:投稿が多いと良い反応ももらえる(良い反応を貰えたから投稿数が増えたとも考えられる)
total_postとbad_reaction:投稿が多いと悪い反応も増える(悪い反応が増えたから投稿が増えたはあまり考えられない、渾身のツイートが1いいねだったら投稿する気失せる)
avg_skillとApprove:最終結果は5つのスキルの平均でした。と説明文にあるので
avg_skillとgood_reaction:能力が高いとよい反応がもらえやすい
good_reactionとbad_reactionについては因果関係が判断できませんでした。
以上から方向づけすると以下のような結果になります。
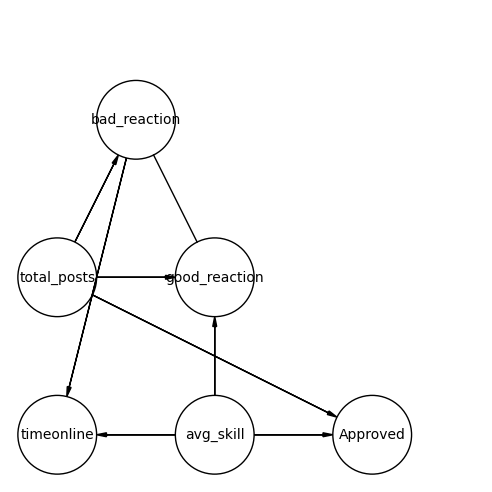
最初の頃と比べたらかなりスッキリしました。
考察
学習時間が増えたから能力が上がったって訳では無く、あくまで能力が高い生徒が学習時間が長いと分かりましたのは驚きでした。
ただ今回の手法も問題点がいくつかあり
- カイ二乗検定を相当な回数やるので偶然的に有意差が出てしまう可能性がある
- すべての向きが分かるわけではなく、やはり人間が考えて推測しないと行けない箇所が多い
- かなり時間かけたわりに当たり前と思える結果もある
のような点が挙げられます。
とはいえ検定を使った因果推論は初めてだったのでとても勉強になりました。
間違い等あればご指摘いただけると幸いです。
参考書籍
本記事は以下の書籍を参考に作成しました。
つくりながら学ぶ! Pythonによる因果分析 ~因果推論・因果探索の実践入門 (Compass Data Science) 小川雄太郎 (著)
前回書いた記事
Discussion