Zenn
Aidemy Tech BlogPublicationへの投稿
👁️

一般化線形モデル (GLM) で予知保全入門

Shingo Nakazawa
2024/08/14に公開
Julia
統計学
mcmc
ベイズ統計
線形回帰
tech

はじめに

こんにちは。株式会社アイデミーデータサイエンティストの中沢(X/Bsky)です。

弊社ではModeloyというDX内製化の伴走支援サービスを提供しており、そこで予知保全に関するご相談をいただくことがあります。
予知保全とはザックリ言うと、センサーやIoTデバイスのデータから、機器の故障や不具合を事前に予測し、適切なタイミングでメンテナンスを行うことで、突発的な故障を防ぎ、機器の稼働率を最大化する取り組みです。修理費用の抑制によるコスト削減や機器停止時間の最小化による機会損失の回避、重大事故の予防による作業者の安全確保などといったメリットが得られます。

本稿では、一般化線形モデル (Generalized Linear Model; GLM) を用いた予知保全のシンプルな実現例をご紹介します。コード例では環境構築の容易さからJulia言語のTuringを用います[1]。Turingの記法については以前の記事をご参照ください[2]。

パッケージの読み込み

最初に必要パッケージをまとめて読み込んでおきましょう[3]。

using Turing, Distributions, StatsPlots, DataFrames, CSV, Plots, Chain

データの読み込みと前処理

今回は模擬データとしてある部品製造会社の生産日誌のようなものを用意しました。生産ラインの様々な要因から不良品の発生率を予測することで、不良品が多く作られてしまう前に対策を講じ不良品数の削減を目指しているような状況を想定します。

データの読み込み

まずは模擬データを読み込みます。全部で100件のデータですが、最初の5件だけを表示します。

df = CSV.read("GLM_dataset.csv", DataFrame)
first(df, 5)

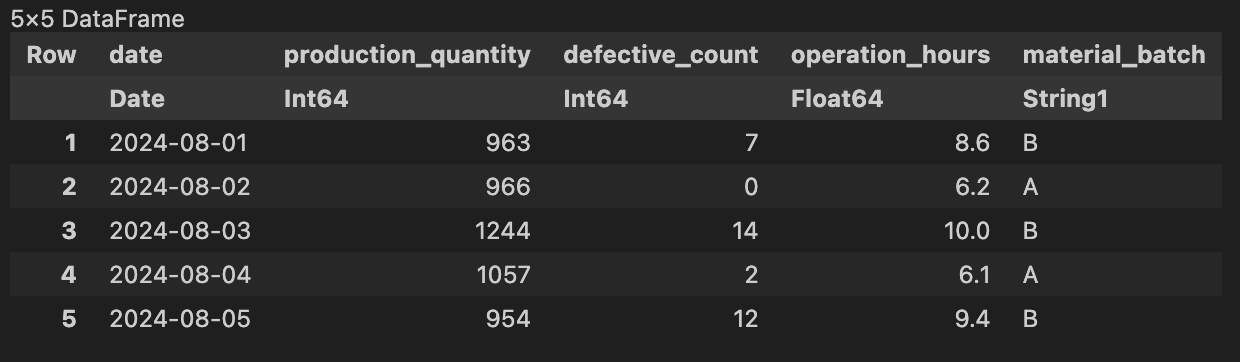
  • 日付 (date)
  • 生産数 (production_quantity)
  • 不良品数 (defective_count)
  • 生産ラインの稼働時間 (operation_hours)
  • 原材料のロット (material_batch)

を含むテーブルです。今回は簡単のために稼働時間と原材料のロットだけから不良品率の予測モデルを構築してみましょう。

前処理

予測モデル構築に先立ち、データの前処理を行います。

最初に、予測対象として不良品率という項目を作ります[4]。

# 不良品率という新しいカラムを作る
df[!, :defective_rate] = df[!, :defective_count] ./ df[!, :production_quantity]
df

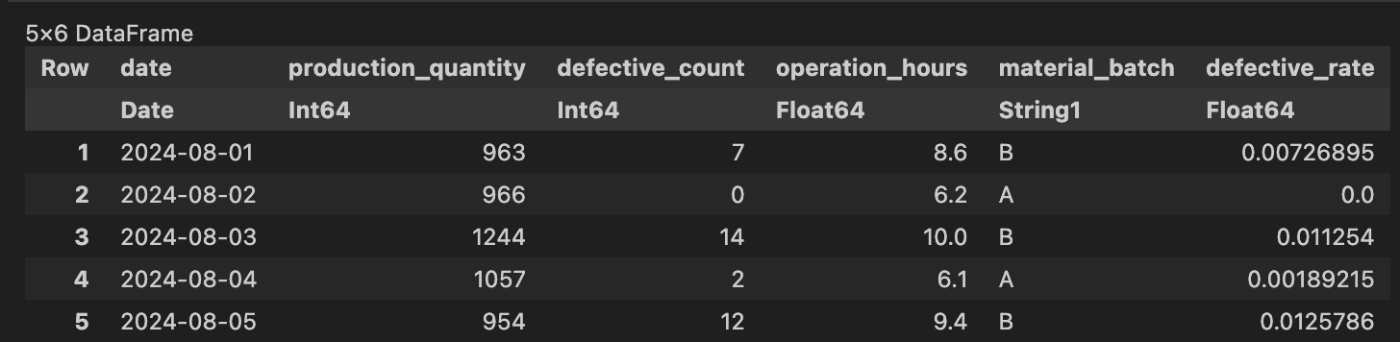
ここで不良品率と説明変数の関係を目で見ておきましょう。

# 不良品率と稼働時間の関係を散布図で確認する
p1 = scatter(df[!, :operation_hours], df[!, :defective_rate], xlabel="Operation Hours", ylabel="Defective Rate", legend=false)
# 原材料ロットごとの不良品率をbox plot
p2 = boxplot(df[!, :material_batch], df[!, :defective_rate], xlabel="Material Batch", ylabel="Defective Rate", legend=false)

plot(p1, p2, layout=(1,2), legend=false)

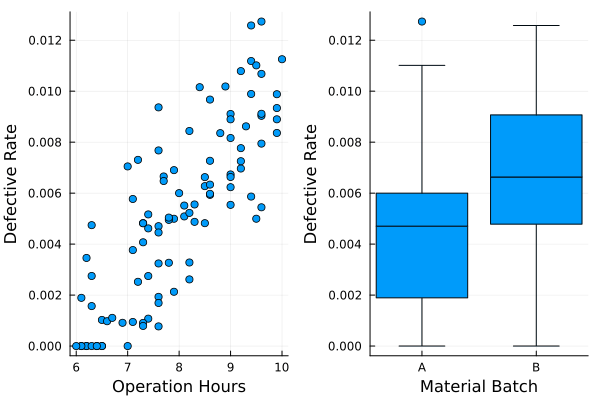
こうしてみると、稼働時間が長くなると不良品数が増えていること、ロットBの方が不良品が多く出現する傾向にあることが見て取れます。

次に、原材料のロットはカテゴリカル変数であるため、ダミー変数化しておきましょう。

# Material batchをOne-hot-encodingに置き換える
encoded_df = @chain df begin
    select(:material_batch, [:material_batch=>ByRow(isequal(v))=>Symbol("batch_is_"*v) for v in unique(df.material_batch)])
    select(Not(:material_batch, :batch_is_A)) # Bか否かだけわかれば十分なので、不要な列を削除
end

processed_df = hcat(df, encoded_df, makeunique=true)
# 不要な列の削除
processed_df = select(processed_df, Not(:date, :material_batch))

first(processed_df, 10)

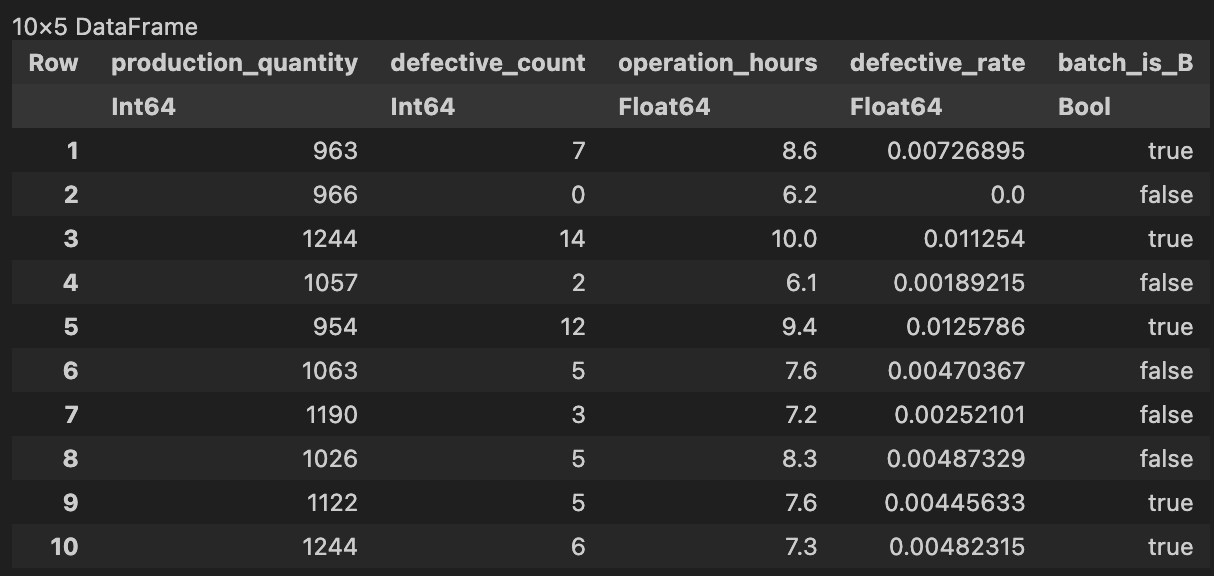
これで準備完了です。

正規分布を用いたモデリング（正規線形モデル）

1つ目の例として正規分布を用いた線形モデルを作ってみましょう。

仮説として、

  • 稼働時間と不良品率の間には線形の関係がある
  • 原材料ロットによって不良品率が異なる
  • 観測される不良品率にはノイズが乗る

を考えます。これをモデル式で表すと、

  • \mu_i = \beta_0 + \beta_{1}x_{1i} + \beta_{2}x_{2i}
  • y_i \sim Normal(\mu_i,\sigma^2)

ここで

  • x_{1i} はi番目のラインの稼働時間
  • x_{2i} はi番目のラインで用いた原材料ロットがBか否か
  • y_{i} はi番目のラインでの生産物の不良率

と書くことができます（これはすなわち重回帰分析と等価です）。

モデル式をTuringのコードに直すと以下のようになります。

@model function glm_normal(x₁, x₂, y)
    # 係数の事前分布。裾の広い正規分布を無情報事前分布的に用いる
    β₀ ~ Normal(0, 100)
    β₁ ~ Normal(0, 100)
    β₂ ~ Normal(0, 100)
    σ ~ Exponential(1)
    
    # モデル式
    for i in 1:length(y)
        y[i] ~ Normal(β₀ + β₁ * x₁[i] + β₂ * x₂[i], σ)
    end
end

MCMCサンプリングを実行します。

# MCMCサンプリング
chain = sample(glm_normal(
    processed_df[!, :operation_hours], 
    processed_df[!, :batch_is_B],
    processed_df[!, :defective_rate]
), NUTS(), 1000)

結果の一部を表示します。

rhatの値から収束していると考えられます[5][6]。

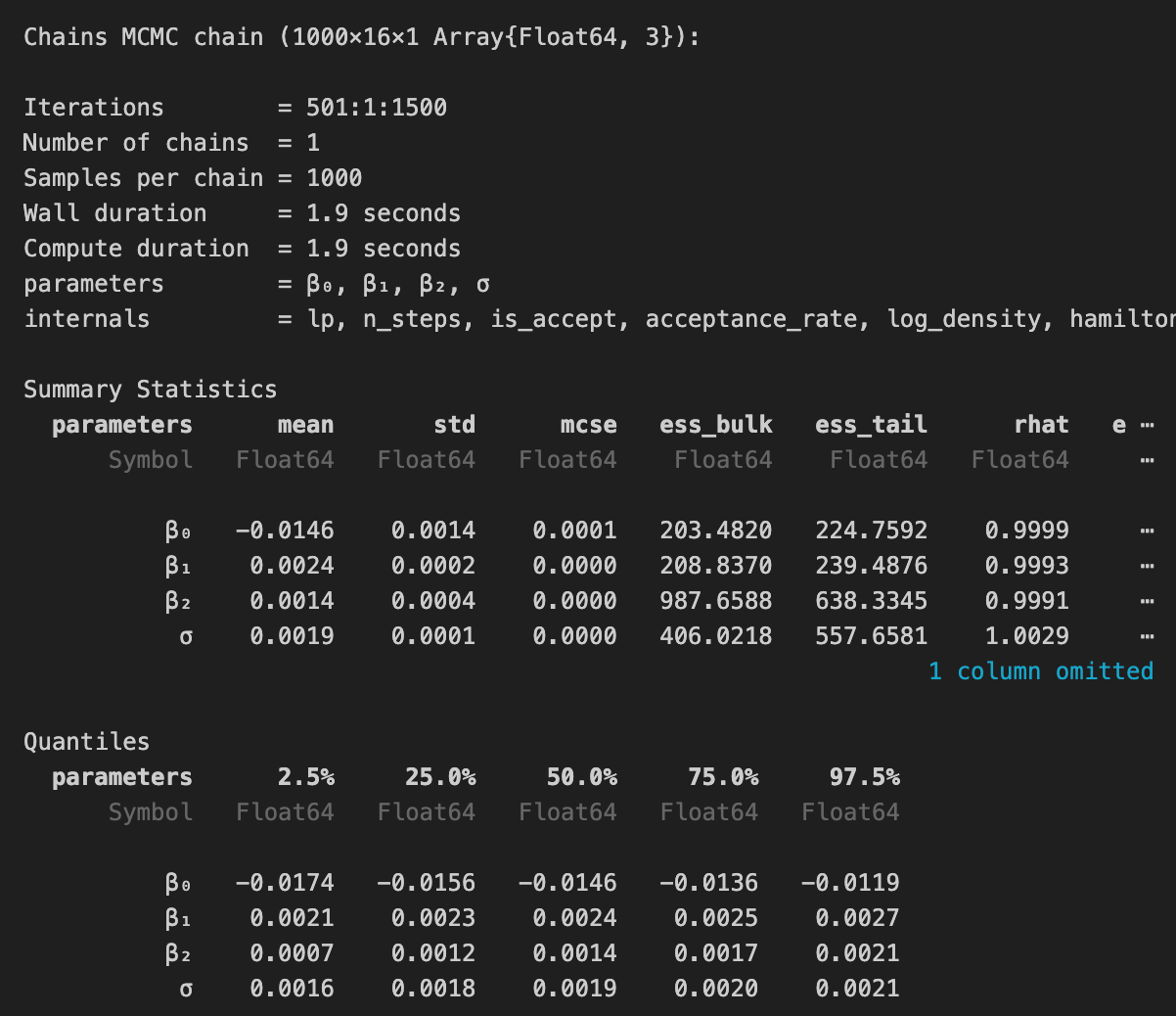
この結果から、

  • \beta_1すなわち稼働時間が1時間伸びるに従って不良品率が0.24%上昇する
  • \beta_2すなわち原材料ロットがBの場合、Aと比べて不良品率が0.14%高い

ということが見て取れます。しかし、このモデルの結果には注意すべき点があります。

サンプリング結果から95%予測区間を可視化してみると、

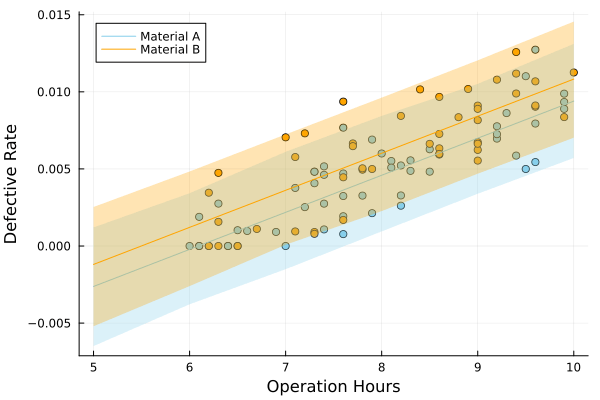
稼働時間が短いときの予測不良品率が負の値になってしまっています。不良率が負というのは現実にありえないので、そもそもの仮定が適切でないと考えられます[7]。

二項分布を用いたモデリング（ロジスティック回帰モデル）

前述のモデルの問題点は、正規分布を仮定しているため、予測される不良品率が0から1の範囲に収まらない可能性があることです。そこで、正規分布を仮定する代わりに、生産数に対して発生した不良品の個数を二項分布で表現します[8]。二項分布の確率（不良品率）が稼働時間と原材料ロットによってどう変化するのかを探ります。

改めて仮説を言葉で表現すると、

  • 稼働時間によって不良品率が変化する
  • 原材料ロットによって不良品率が異なる
  • 不良品率は0から1の範囲内にある

と書くことができ、これをモデル式で表すと、

  • logit(p_i) = \beta_0 + \beta_{1}x_{1i} + \beta_{2}x_{2i}
  • y_i \sim Binomial(n_i, p_i)

ここで

  • logit(p_i) は不良品率のロジット変換
  • x_{1i} はi番目のラインの稼働時間
  • x_{2i} はi番目のラインで用いた原材料ロットがBか否か
  • y_{i} はi番目のラインでの不良品数
  • n_i はi番目のラインでの生産数

となります[9]。これをTuringのコードに直すと、以下のようになります。

invlogit(x) = 1 / (1 + exp(-x))

@model function glm_binomial(x₁, x₂, y, n)
    # 係数の事前分布。裾の広い正規分布を無情報事前分布的に用いる
    β₀ ~ Normal(0, 100)
    β₁ ~ Normal(0, 100)
    β₂ ~ Normal(0, 100)
    
    # モデル式
    for i in 1:length(y)
        p = invlogit(β₀ + β₁ * x₁[i] + β₂ * x₂[i])
        y[i] ~  Binomial(n[i], p)
    end
end

このモデルでMCMCサンプリングを実行。

# MCMCサンプリング
chain = sample(glm_binomial(
    processed_df[!, :operation_hours], 
    processed_df[!, :batch_is_B],
    processed_df[!, :defective_count],
    processed_df[!, :production_quantity]
), NUTS(), 1000)

結果の一部を表示します。

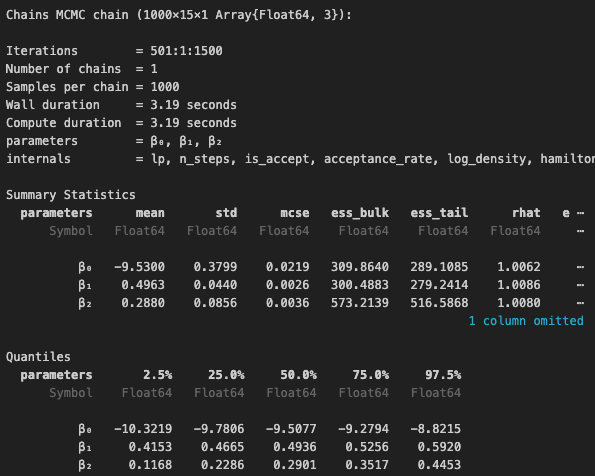
rhat < 1.1から、モデルが収束していると判断できます[10]。

不良品数→不良品率に変換しつつ、95%予測区間を可視化します。

# 予測分布を計算
hour_pred = collect(5:1:10) # 予測する稼働時間の範囲
production_quantity_pred = 1000 # 何個生産したときの値を予測するか

p_A = invlogit.(chain[:β₀] .+ chain[:β₁] .* hour_pred')
y_A = rand.(Binomial.(production_quantity_pred, p_A))
y_A_mean = mean(y_A, dims=1)'

p_B = invlogit.(chain[:β₀] .+ chain[:β₁] .* hour_pred' .+ chain[:β₂])
y_B = rand.(Binomial.(production_quantity_pred, p_B))
y_B_mean = mean(y_B, dims=1)'

# 95% 予測区間
lower_A = [quantile(y_A[:, i], 0.025) for i in 1:size(y_A, 2)]
upper_A = [quantile(y_A[:, i], 0.975) for i in 1:size(y_A, 2)]

lower_B = [quantile(y_B[:, i], 0.025) for i in 1:size(y_B, 2)]
upper_B = [quantile(y_B[:, i], 0.975) for i in 1:size(y_B, 2)]

# 予測分布の可視化
p = scatter(processed_df[!, :operation_hours], processed_df[!, :defective_rate], 
    xlabel="Operation Hours", ylabel="Defective Rate", 
    color=ifelse.(processed_df[!, :batch_is_B], :orange, :skyblue),
    label="", legend=:topleft)
# 不良品率をプロットするため、予測された不良品数をproduction_quantity_predで割る
plot!(p, hour_pred, y_A_mean/production_quantity_pred, ribbon=((y_A_mean .- lower_A)/production_quantity_pred, (upper_A .- y_A_mean)/production_quantity_pred), fillalpha=0.3, label="Material A", color=:skyblue)
plot!(p, hour_pred, y_B_mean/production_quantity_pred, ribbon=((y_B_mean .- lower_B)/production_quantity_pred, (upper_B .- y_B_mean)/production_quantity_pred), fillalpha=0.3, label="Material B", color=:orange)

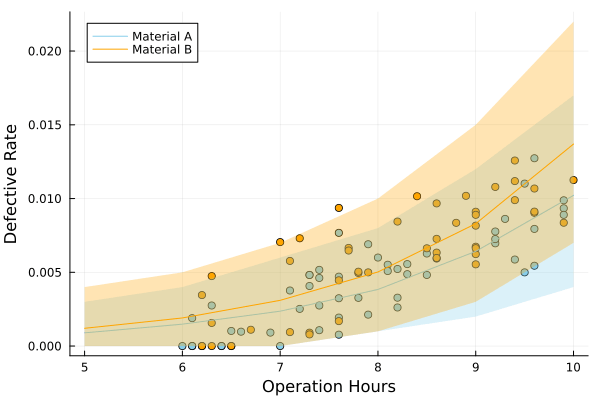
今回のモデルでは不良品率が負の値を取らず、0以上の値に収まっていることが確認できます[11]。

(Appendix) ロジスティック回帰モデルの係数の解釈

ロジスティック回帰モデルの係数の解釈は少し複雑です。今回程度にシンプルであれば図を見て解釈するのが最も簡単なのですが、数字を追う際にはオッズ比への変換が必要となります。

オッズとは「成功する確率と失敗する確率の比率」を表した指標で odds = \frac{p}{1-p} で計算されます（pは不良品率）。

オッズの変化率はオッズ比と呼ばれ、ロジスティック回帰の係数の指数、すなわち \exp(\beta_i) に一致します。これは x_i が1単位増加したときに、不良品が発生するオッズが何倍になるかを表します。

今回の例の場合、\beta_1 = 0.496 より、オッズ比は \exp(0.496) \approx 1.64 となり、稼働時間が1時間増加すると、不良品が発生するオッズが1.64倍になることを意味します。

「オッズが1.64倍」と言われてもなかなか行動に繋げづらいので、具体的に不良品率がどう変化するか計算してみましょう。

  • ロットAのラインで稼働時間が約8.5時間を基点とすると、不良品率の予測平均値が0.5%なので、オッズは\frac{0.005}{1-0.005} \approx 0.00503
  • 稼働時間が1時間伸びると新しいオッズは 0.00503 \times 1.64 \approx 0.00824となり、新しい確率は \frac{0.00824}{1+0.00824} \approx 0.00817となり、不良品率が0.817%になる
  • ロットBに変えたときには、\beta_2 = 0.288よりオッズ比は \exp(0.288) \approx 1.33、
    新しいオッズは 0.00503 \times 1.33 \approx 0.00670より、新しい確率は \frac{0.00670}{1+0.00670} \approx 0.00666となり、不良品率が0.666%になる

と計算することができます。図示された結果と一致していることが確認できました。

予測結果から予知保全へ

ここまでの結果より、稼働時間がどのくらい伸びると不良品率がどの程度増えるか、ロットが変わるとどの程度不良品率が増えるかを、楽観的・悲観的な立場から（すなわち予測区間という幅を持って）予測することができました。この分析結果を持って保全スケジュールを立てていくことになります。

ここから先はビジネスモデル次第で大きく変わるところですが、例えば

  • 不良品率が◯◯を超えると品質管理観点から許容できない
  • ロットAのときに不良品率が◯◯を超える可能性が出てくるのは△時間稼働したとき。□時間稼働するとほぼ確実に危険水準
  • ロットBのときに・・・
  • ロットAを使うラインは☆時間動かしたら、Bを使うラインは◇時間動かしたら一度メンテナンスをするようにしよう

といった判断が行えます。これができるとメンテナンススケジュールの最適化・自動設計が次に見えてきます。メンテンナンスにかかるコストや人手、時間の制約の中で不良品の発生数を最小化するには？（あるいは利益を最大化するには？）のような数理最適化の問題になります。

また、今回の予測を通して、この生産ラインそのものに対する理解を深めるきっかけも得られます。

  • 稼働時間が伸びると不良品率が増えるのはどうしてだろう？
  • ロットBは何故不良品が増えるのだろう？
  • 累積の使用回数ももモデルに組み込んでみるとどうだろう？
  • 操縦者の熟練度は関係するだろうか？

などといった調査・モデルの改良を通し、そもそもの不良率の低減施策にも繋げられます。

データへの深い理解を通じて不良率を減らし、さらに不良品の数が増える前に効率的にメンテナンスを行うことで、冒頭に挙げたような予知保全の様々なメリットを得ることができるでしょう。

おわりに

本稿では一般化線形モデルを用いた予知保全の一例をご紹介しました。今回はシンプルな模擬データを用いたため、結論は散布図から得られる印象と変わりありませんでしたが、実際の課題では、様々な要素が絡み合い、表面的には見えない複雑な関係が存在することが多々あります。データが生成される過程が複雑になってきたときにこそ、計算機の力を使った分析・予測が大きな価値を発揮します。

一般化線形モデルを発展させることで、現実の問題に対してより精度の高い予測や洞察を得られるようになります。例えば、不良品率に関係しうる全ての要素のデータの取得は現実的ではありませんが、観測できていない要素の存在を仮定し、それによる変動をモデルに組み込む手法もあります。
また、本稿では日付列を削除しましたが、いつ取得されたデータかという情報を積極的に活用し、季節性やトレンドも考慮するモデリング手法もあります。
データが非線形の関係を持つ場合や外れ値が多い場合には、データの特性に応じたモデル選択・設計を行うことで、より柔軟なモデリングができるようになります。

利用できる情報が豊富な場合は既存の機械学習パッケージを活用すれば迅速かつ効果的にモデリングを行うこともできるでしょう。しかし、情報が限られている状況では分析者独自の創意工夫が必要になります。こうした状況でこそ、本稿で紹介したような柔軟性の高い手法が大きな強みを発揮します。

本稿が皆様のデータ分析の足がかりとなれば幸いです。

更新履歴

2024-08-15: 誤字修正。「予測結果から予知保全へ」内の表現を一箇所修正。

脚注

  1. Juliaにそこまで習熟しているわけではないので、変な書き方をしている部分があるかもしれません。そういった点もご指摘いただけますと大変嬉しく思います。 ↩︎

  2. TuringからPyMCやStanなどへの書き換えが比較的容易であることも1つの理由。まぁ今どきはLLMに放り込めば大概何とかなるのですが。 ↩︎

  3. パッケージのインストール方法については以下の記事の手順4,5をご参照ください。https://zenn.dev/aidemy/articles/c5919502cb1b2e#手順4%3A-juliaのプロジェクト作成 ↩︎

  4. 今回は生産数（分母）が近しい、十分に大きい値なので割り算値を用いて進めますが、割り算値が適当にデータを表現できているかは要注意。同じ3割バッターでも500打数150安打と10打数3安打では全く異なりますよね。 ↩︎

  5. “Inference and Monitoring Convergence.” Markov Chain Monte Carlo in Practice, Chapman and Hall/CRC, 1995, pp. 149–162. http://dx.doi.org/10.1201/b14835-13 ↩︎

  6. rhatの数値だけでなく事後分布のplotも確認すべきですが、本稿ではスペースの都合上割愛。 ↩︎

  7. 必ずしも「正規分布を用いたモデリングが今回の対象に対し使えない」とは言い切れません。正規分布を用いたモデリングは解釈性が高く扱いやすいので、不良品率が負にならない領域の予測のみが対象となっているのであれば「モデルの限界を正しく認識した上で」用いるのはアリでしょう。特に今回は不良品率と稼働時間の間に明確な直線関係があるので、こちらの方が適当と考えることもできます。 ↩︎

  8. 正規分布に限らず様々な分布を使えるため、「一般化」線形モデルと言われる。 ↩︎

  9. モデル式ではリンク関数を第一式の左辺に置くのが一般的です。しかし、なぜそうするのかは把握できていません。慣習上の問題？ご存知の方がおられたら教えていただけると嬉しいです。 ↩︎

  10. こちらも事後分布のプロットは省略。 ↩︎

  11. 正規分布と二項分布のどちらが「正しい」モデルかという議論はできません。いずれも「モデル」であり、どの仮説に基づいて分析ひいては意思決定を行うのかという意志が重要です。 ↩︎

Aidemy Tech Blog
Aidemy Tech BlogPublication

株式会社アイデミーの技術ブログです。

Discussion