JuliaのTuringでベイズモデリング - 導入編

はじめに

こんにちは。株式会社アイデミーデータサイエンティストの中沢(X/Bsky)です。

7月に入ってからBDA3の邦訳版であるベイズデータ解析（第3版）や渡辺澄夫ベイズ理論100問 with Python/Stanが刊行されるなど、ベイズ統計が改めて注目を集めています。これを機にベイズ統計を本格的に学びたいと考えている方も多いでしょう。しかし、勉強を進めていく過程で1つのハードルとして立ちはだかるのが「どうやって近似推論・MCMCを実装するか」という問題です。

数式を一からフルスクラッチで書いていく方針もあれば、手軽に始められるライブラリやフレームワークを利用する方針もあります^[1]。PythonではPyMCやPyStanが、RではRStanが有名ですね。

一方で、これらのライブラリを使おうとするとそもそも環境構築でコケてしまうことが多々あります。PyMCにしろRStanにしろ、インストールしただけでは動かないことはざらで、「前は動いていたのに今日は動かない」なんてこともあります。

環境構築でつまずいて、この面白い分野を諦めてしまうのは本当にもったいないことです。
そこで本稿では環境構築の容易さからJulia言語に着目し、JuliaのTuringライブラリを使ったベイズモデリングの実装例を紹介します。

なぜJuliaか

環境構築が用意

Juliaというと「Pythonのように簡単に書くことができ、Cのように高速に動作するものを目指した^[2]」というフレーズや「数値計算やデータ分析のための言語なんだ」というところばかりが注目されがちですが、実は環境構築が非常に容易で使い始めるまでのハードルがとても低いことも強みである言語です。個人的にはこの点こそがJuliaを人に勧める一番の理由と言っても過言ではないくらいに Pythonに辟易している Juliaのセットアップの簡便さは魅力的です。
具体的にはインストールとこちらの記事の手順4, 5のみで準備完了です^[3]。

数学に近い書き方ができる

Juliaは数式をそのままコードに反映できる直感的な文法をもっており、Unicodeにも対応しています。そのため、教科書や論文中で使われている記号をそのままコードに写すことができます。例えば、線形回帰モデルを定義する場合は以下のように書けます。

using Turing

@model function linear_regression(x, y)
    α ~ Normal(0, 10)
    β ~ Normal(0, 10)
    σ ~ Exponential(1)
    
    for i in 1:length(y)
        y[i] ~ Normal(α + β * x[i], σ)
    end
end

~ や α, βと、紙面上で見た数式をほぼそのままコード中に表現できます。

高速なパフォーマンス

JuliaはC言語に匹敵する高速な数値計算が行えます。計算が速いと試行錯誤のサイクルを多く回せますし、実運用でも高いパフォーマンスが期待できます。また例えば、テーブルデータの処理ではPythonやRでは行列計算を一般に前提としますが、Juliaではforループを用いた処理でも十分に高速です。実装がシンプルで理解しやすいことは、データがどう加工されているかを追跡しやすいため、データに基づいた意思決定において非常に大きなメリットとなります。

Turingを用いたベイズモデリングの実装

本稿では、Juliaの確率的プログラミングライブラリであるTuring.jlの基本を、線形回帰の実装例を通しさらいます^[4]。

Turingのインストール

まず、JuliaのREPLで]を押しパッケージモードに入り、プロジェクトを作成します。

julia>
# ] を押すとパッケージモードに入る
(@v1.10) pkg> 

(@v1.10) pkg> activate .
Activating project at `[作業ディレクトリ]`
([作業ディレクトリ名]) pkg>

次に、Turing.jlをインストールします。ついでに可視化に使うパッケージも入れておきましょう。

pkg> add Turing DataFrames CSV Distributions Plots StatsPlots

データの準備

今回は乱数から適当に生成したモックデータを用います^[5]。ここから先はJupyter notebook上で動かす想定で記載を行います^[6]。

using DataFrames, CSV

df = CSV.read("mock_data.csv", DataFrame)
df

全部で100行のデータですが、ここでは最初の8行のみ表示しています。散布図を描くと以下のようになります。

using Plots

x_obs = df[!, :x]
y_obs = df[!, :y]
scatter(x_obs, y_obs, label="data", xlabel="x", ylabel="y")

仮説の記述

上図から $x$と$y$の間には線形の関係があると推測できます。さらに観測される$y$には正規分布に従うノイズが加わると仮定できそうに感じます。

この仮説をモデル式で表すと、

• $\mu = \beta_0 + \beta_1 * x$
• $y \sim Normal(\mu, \sigma)$

と書くことができます。仮説が適切だとした場合、それぞれのパラメータがとる値はどのようなものになるか（点推定）・どの程度の幅を持ちうるか（区間推定）を明らかにすることを分析の目的とします^[7]。

モデルの定義

上記のモデル式をTuringのドキュメンテーションを参考にコードに書き下していきます。

using Turing

@model function linear_regression(x, y)
    # パラメータの事前分布
    β₀ ~ Normal(0, 10)
    β₁ ~ Normal(0, 10)
    σ ~ Exponential(1)

    # モデル式
    for i in 1:length(x)
        y[i] ~ Normal(β₀ + β₁ * x[i], σ) 
    end
end

MCMCサンプリングの実行

Turingでのサンプリングは非常に簡単で、以下の一文で完了します^[8]。

# MCMCサンプリング
chain = sample(linear_regression(x_obs, y_obs), NUTS(), 1000)

結果の一部を以下に表示します。

Iterationsが501から始まっているように、warmupは自動的に設定されます。明示的に行いたい場合は NUTS(500, 0.65) のようにサンプリングアルゴリズムの引数で指定します^[9]。

Iterationsの二つ目の数字はthinningの値です。デフォルトは1ですが、sample()の引数に例えば thinning=6 と加えることで設定を変更できます。

複数chainでサンプリングを行うには例えば

chain = sample(linear_regression(x_obs, y_obs), NUTS(), MCMCThreads(), 1000, 4)

とすることで、4つのchainを得ることができます^[10]。

chainから特定のパラメータのサンプリングデータを得たい場合は以下のように行います。

chain[:β₀]

複数chainある場合は複数列のMatrixとして取得されます。

事後分布の可視化

得られたchainからの事後分布の可視化は以下のように行えます。

using StatsPlots

plot(chain)

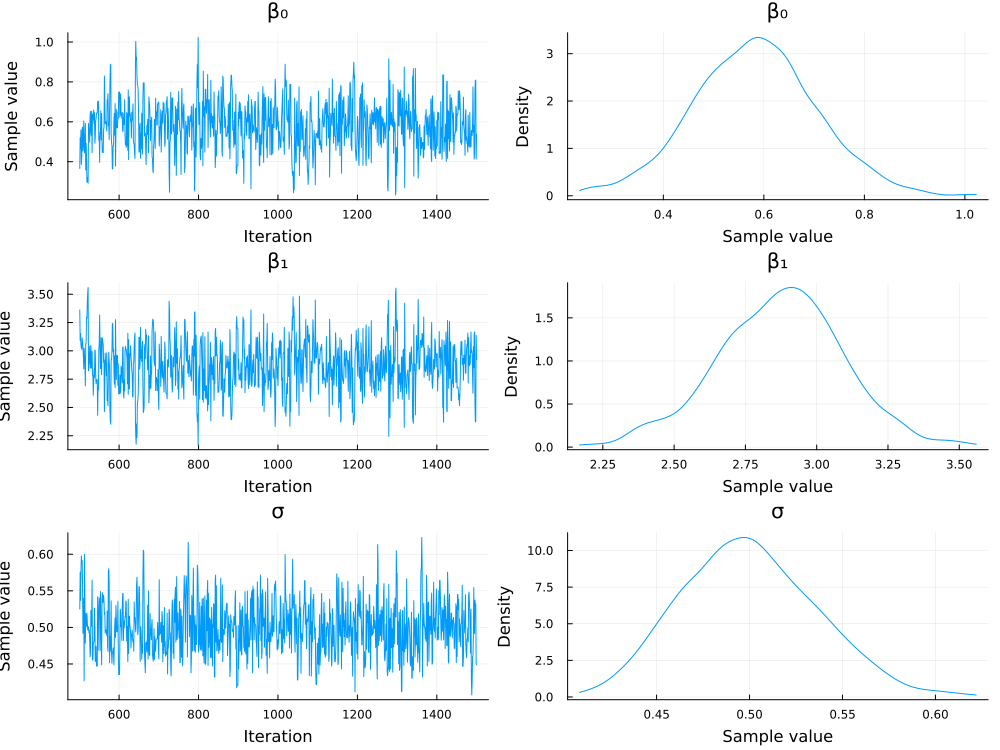
複数のchainのサンプリングを行った場合はchainごとに色分けされて図示されます。

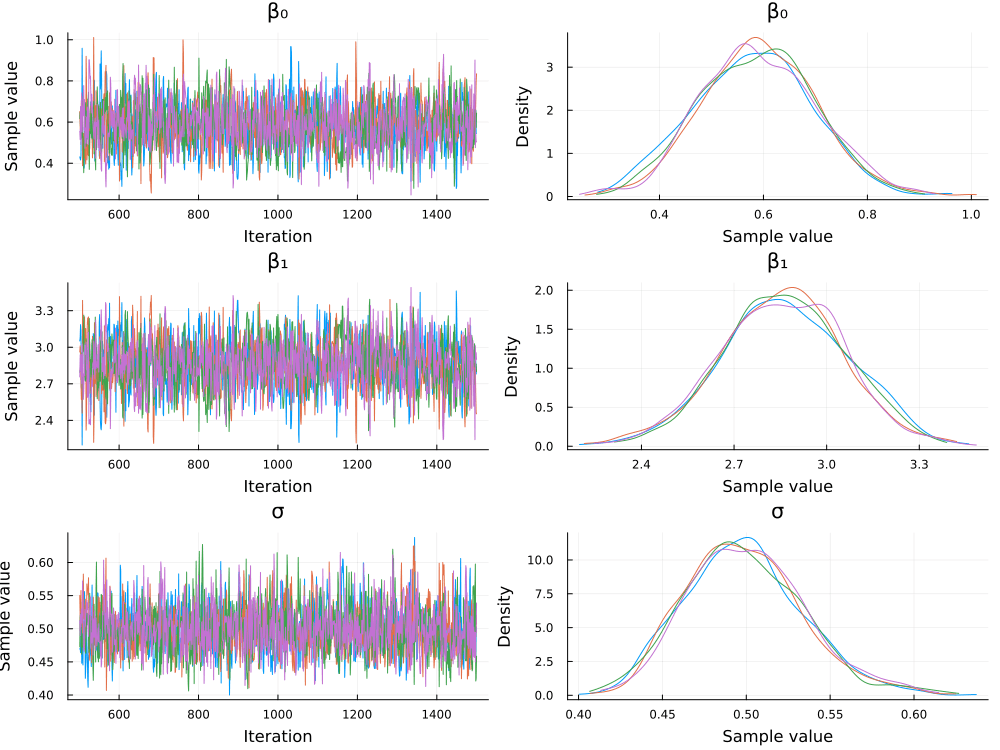
先の結果サマリーで rhatが1.1を下回ることが収束の基準としてよく用いられますが、事後分布プロットの定性的な見た目と合わせて判断するのが実践的なように思います^[11]。

回帰直線と予測分布の可視化

最後に回帰直線と95% 信用区間、95% 予測区間の可視化を行います^[12]。

# 予測分布を計算
x_pred = collect(0:0.1:1)
μ_pred = chain[:β₀] .+ chain[:β₁] .* x_pred'
y_pred = rand.(Normal.(μ_pred, chain[:σ]))

y_pred

# 95% 信用区間
lower_μ = [quantile(μ_pred[:,i], 0.025) for i in 1:length(x_pred)]
upper_μ = [quantile(μ_pred[:,i], 0.975) for i in 1:length(x_pred)]

# 95% 予測区間
lower_y = [quantile(y_pred[:,i], 0.025) for i in 1:length(x_pred)]
upper_y = [quantile(y_pred[:,i], 0.975) for i in 1:length(x_pred)]

# 予測分布の可視化
scatter(df[!, :x], df[!, :y], label="observed data", xlabel="x", ylabel="y")
μ_pred_mean = mean(μ_pred, dims=1)'
plot!(x_pred, μ_pred_mean, ribbon=(μ_pred_mean .- lower_μ, upper_μ .- μ_pred_mean), fillalpha=0.2, label="95% Credible Interval")
plot!(x_pred, μ_pred_mean, ribbon=(μ_pred_mean .- lower_y, upper_y .- μ_pred_mean), fillalpha=0.2, label="95% Prediction Interval")

オレンジが95% 信用区間、緑が95% 予測区間を表します。今回は予測区間内に観測データのほとんどが収まっていることが見て取れます。
95% 予測区間から観測データが多くはみ出していたら、モデル構造を修正するべきでしょう。

結果の考察

パラメータの期待事後推定値 (Expected A Posteriori; EAP) は以下の通りです。

• $\beta_0$ (切片) の EAP: 約 0.58
• $\beta_1$ (傾き) の EAP: 約 2.87
• $\sigma$ (標準偏差) の EAP: 約 0.50

これらの値から、観測データは $y \sim Normal(0.58 + 2.87 * x, 0.50)$ によって近似的に表現できると考えられます。

また、$\beta_0$の95%信用区間から、$x$ が1増加したときの $y$ の予測される増加量は2.46~3.25の範囲内におおよそ収まると考えられます。

分析結果のどこにどう着目するか・そもそもどういう仮説でモデルを構築するかは目的次第です。チュートリアルの本記事では上記程度の考察しかできていませんが、実践では「こんなところでも使えるのか」と驚くほど多種多様な解析にベイズモデリングが用いられています。

（Appendix）事前分布からのサンプリングの実行

ベイズモデリングでは、学習前のモデルから具体的なパラメータやサンプルを得ることによって、仮説がカバーしている実現例を視覚的に確認できます。ここで例えば $y$ が上限・下限を超えたり、非現実的な値に偏って出力されたりしていれば、そもそもモデルのデザインに問題があると判断できます。

TuringではPriorサンプラーを使うことで実行が可能です^[13]。

chain = sample(linear_regression(x_obs, y_obs), Prior(), 1000) # Priorサンプラーを使用

# 予測分布を計算
x_pred = collect(0:0.1:1)
μ_pred = chain[:β₀] .+ chain[:β₁] .* x_pred'
y_pred = rand.(Normal.(μ_pred, chain[:σ]))

# 95% 信用区間
lower_μ = [quantile(μ_pred[:,i], 0.025) for i in 1:length(x_pred)]
upper_μ = [quantile(μ_pred[:,i], 0.975) for i in 1:length(x_pred)]

# 95% 予測区間
lower_y = [quantile(y_pred[:,i], 0.025) for i in 1:length(x_pred)]
upper_y = [quantile(y_pred[:,i], 0.975) for i in 1:length(x_pred)]

# 予測分布の可視化
scatter(df[!, :x], df[!, :y], label="observed data", xlabel="x", ylabel="y", title="Prior Prediction")
μ_pred_mean = mean(μ_pred, dims=1)'
plot!(x_pred, μ_pred_mean, ribbon=(μ_pred_mean .- lower_μ, upper_μ .- μ_pred_mean), fillalpha=0.2, label="95% Credible Interval")
plot!(x_pred, μ_pred_mean, ribbon=(μ_pred_mean .- lower_y, upper_y .- μ_pred_mean), fillalpha=0.2, label="95% Prediction Interval")

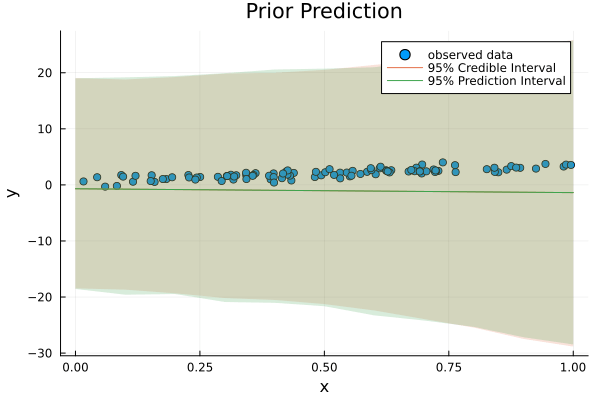
今の事前分布からのサンプリングは広い範囲に及んでいます。これは、パラメータに関する事前知識を全く与えていないことを反映しています。

「目的変数が負の値を取らない」や「パラメータが特定の範囲内に収まる」など、何かしらの事前知識がある場合は、ある程度の「入れ知恵」をすることで学習効率を大幅に改善できることもあります^[14]。

おわりに

本記事では、JuliaとTuringを用いたベイズモデリングの簡単な実装例を紹介しました。Juliaの環境構築の容易さ、直感的な文法、高速なパフォーマンスを活かして、ベイズモデリング習熟の足がかりとしていただければ幸いです。

ご意見やご質問がありましたらコメント欄やX、Blueskyでお気軽にご連絡ください。

脚注

1. 個人的には、まず須山先生のJuliaで作って学ぶベイズ統計学を参考にJuliaの基礎文法を知る＋自分でアルゴリズムを書いてベイズ統計の考え方を理解し、その後にライブラリを使って教科書や論文を再現し実践的な使い方を学ぶという順番がおすすめ。

2. Why We Created Julia https://julialang.org/blog/2012/02/why-we-created-julia/

3. Pythonと連携したい、VSCodeで使いたいという際には他の手順もご参照ください。

4. 自分もJuliaにそこまで習熟しているわけではないので、変な書き方をしている部分があるかもしれません。そういった点もご指摘いただけますと大変嬉しく思います。

5. LLMに適当に作ってもらいました。

6. 本稿では必要なパッケージを都度読み込んでいますが、実際には最初にまとめて読み込む方が良いと思います。

7. 予測の不確実性を同時に評価できることがベイズモデリングの大きな強み。

8. NUTS以外のサンプラーももちろん選べますし、外部のサンプラーを用いることも可能です。 https://turinglang.org/docs/tutorials/docs-15-using-turing-sampler-viz/#samplers

9. 第2引数の0.65はターゲットの採用率。多くの場合において適切なパフォーマンスを得られるデフォルト値として広く使用されている。

10. それぞれの引数の詳細は公式ドキュメント参照。 https://turinglang.org/docs/tutorials/docs-12-using-turing-guide/#sampling-multiple-chains

11. 例えば、事前分布の設定や範囲の制約に無茶があるとプロットに変な偏りが表れます。どう偏っているかが改善のヒントとなります。

12. 95% 信頼区間と混同されがちだが別物なので要注意。

13. 引数をmissingにする方法が公式ドキュメンテーションでは示されているが、観測値のサンプルサイズに依存するモデルではその方法は使えない。 https://turinglang.org/docs/tutorials/docs-12-using-turing-guide/#sampling-from-an-unconditional-distribution-the-prior

14. やりすぎるとそれはそれで問題。特にステークホルダーを説得する場面では事前設定の根拠を説明できることは必須。どこまでの知識、どこまでの主観を入れていいのかも結局は目的と状況による。（そもそも不適切な分析になっているというのは問題外）