🗂

Multiple Factor Analysisで質的に異なるデータを統合し分析する

Shingo Nakazawa

2024/02/15に公開

はじめに

こんにちは。株式会社アイデミーデータサイエンティストの中沢(X/Bsky)です。

みなさまは複数の実験から集めたデータを分析する際に、実験間のバランスを取って要約・可視化したいと思われたことはありませんでしょうか。例えば、「アンケートデータとセンサーデータ」であったり、「官能評価と成分評価」であったり、質的に異なるデータをまとめて分析したいという場面はときどき出てくるかと思います。そのような場面で使える手法として、本稿では多因子分析 (Multiple Factor Analysis: MFA) を紹介します。

Multiple Factor Analysis (MFA) とは

MFAとは、いくつかのグループが合わさったようなデータテーブルを分析するための手法の一つです。
イメージとしては、

それぞれのブロックごとに主成分分析 (Principal Component Analysis: PCA) を適用し
ブロック間のスケールをノーマライズし
ブロックを再統合して全体にPCAを適用する

ような感覚です^[1]。

MFAの強力な点は大きく二つ挙げられます。

一つは、線形手法であるため計算効率が良く、解釈も容易で、その妥当性も高い点です^[2]。t-SNEやUMAPなどの非線形次元削減法は解釈が難しく、恣意的な結論を導かないように注意が必要ですが、線形手法であればそこまでの心配はありません^[3]。

もう一つが、先にも述べましたが質的に異なる要素を統合できる点です^[4]。

アンケートデータとセンサーデータ
官能評価と成分評価
水質調査と微生物相
ゲノミクスとトランスクリプトミクス

を合わせるようなことも考えられますし、

個人をブロックとみなしてのアンケート分析
評価者をブロックとみなしての官能評価
異なる日に計測された時系列データ

のように、同質のデータを由来ごとにバランスさせるような使い方もできます。しかもMFAを用いる場合は、アンケートや官能評価の項目がブロック間で異なっていても構いません。
さらに、MFAはカテゴリカル変数があっても適用可能なので、カテゴリカル変数をどう前処理するかを考える手間も不要です^[5]。

ここまで聞くと良いことばかりですね。実装が難しいんじゃないか？いえ、Rなら簡単です^[6]。

Rでの実装

本稿ではRのFactoMineRパッケージを用います。

パッケージのインストール

install.packages("FactoMineR")

データの読み込み

今回はFactoMineRに入っているワインの評価データを用います。

library(FactoMineR)
data(wine)

21銘柄のワインに対し、31項目の評価が行われています。

最初の2項目は、ワインの由来を示すラベルです。

次の5項目は、スワリング前の香りに関する評価です^[7]。

次の3項目は、見た目に関する評価です。

次の10項目は、スワリング後の香りに関する評価です。

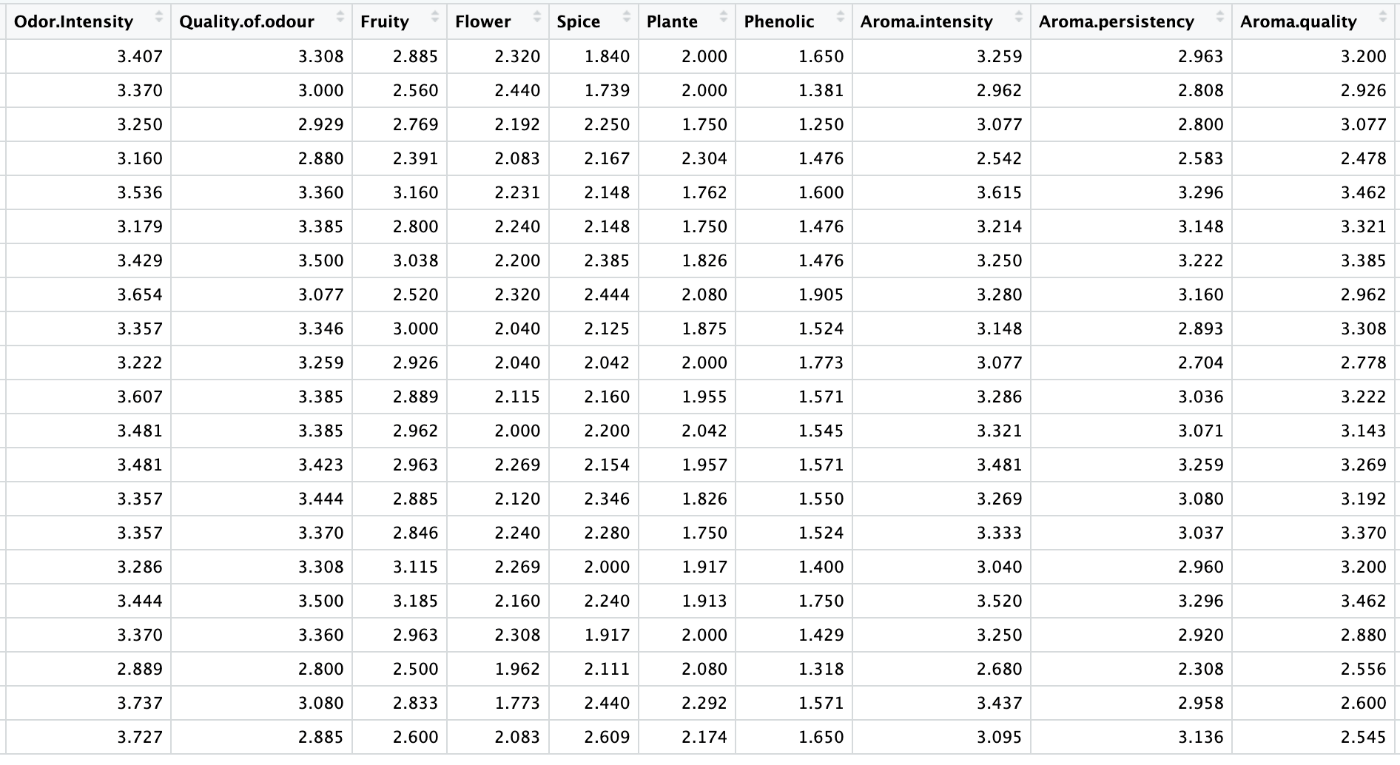
次の9項目は、味に関する評価です。

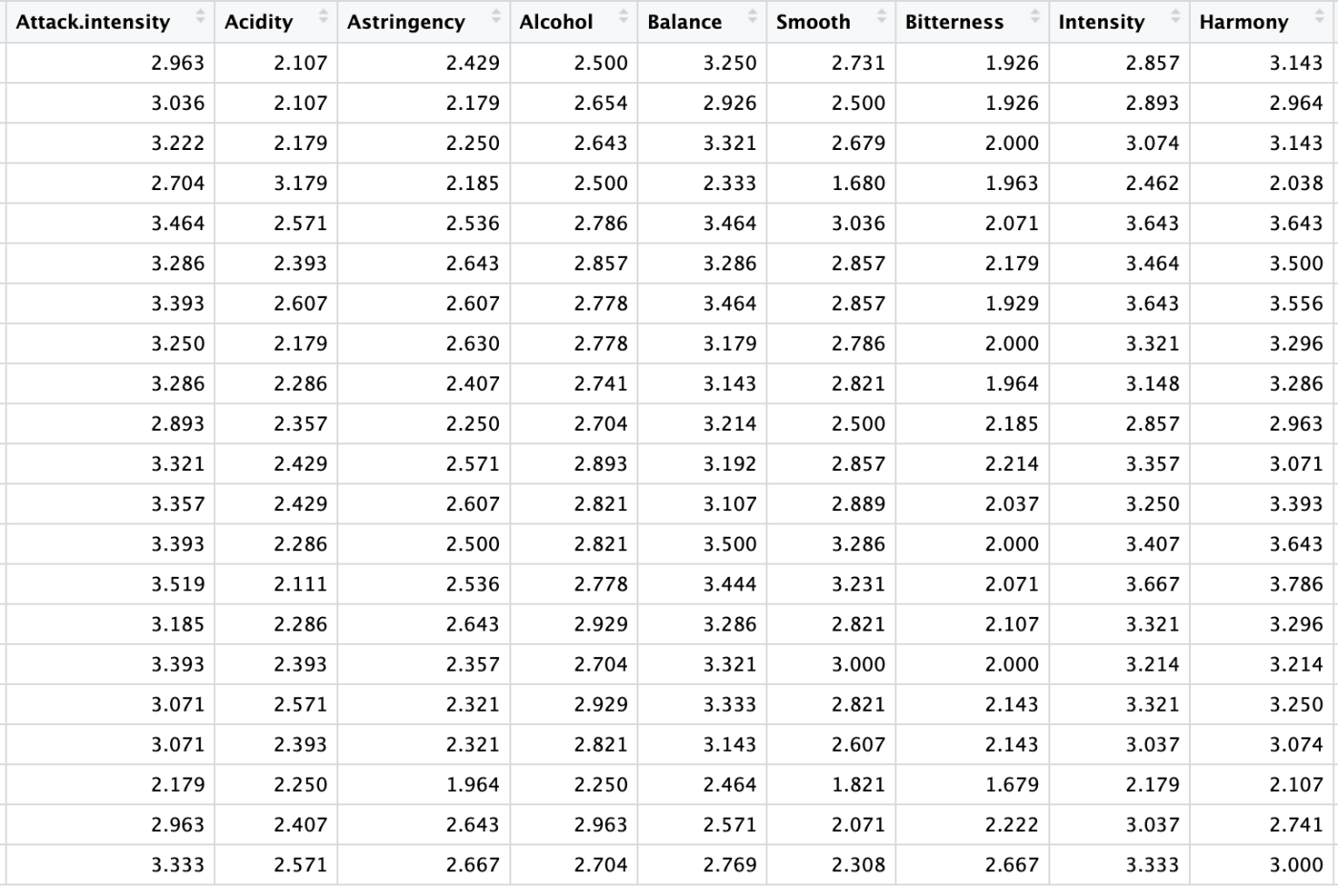
そして、最後の2項目は総評です。

このように、6つのブロックからなるデータとなっています。

MFAを実行する

上記のデータにMFAを適用します。

res.mfa <- MFA(
  wine, # データ
  group = c(2, 5, 3, 10, 9, 2), #　ブロックごとの要素の数
  type = c("n", "s", "s", "s", "s", "s"),　#　ブロックごとの要素の型
  name.group = c("origin","odor","visual", "odor.after.shaking", "taste","overall"), # 各ブロックの名前
  num.group.sup = c(1, 6), # MFAのフィッティングに使わないブロックを指定。デフォルトはNULL
  graph = TRUE # 分析結果グラフを表示するか否か
)

引数について、typeでは、

カテゴリカル変数: n
量的変数: c または s (sだと分析前に標準化される)
頻度: f

をデータブロックごとに指定します。
また、本分析においてはワインの由来と総評のブロックをMFAのフィッティングから除外したいので、num.group.supで何番目のブロックを使わないかを指定しておきます。

結果の可視化と解釈

上記のMFAをgraph=TRUEで実行すると6つのプロットが生成されます^[8]。

2次元での銘柄のプロット

まずはMFAで統合したデータを2次元に要約したプロットです。

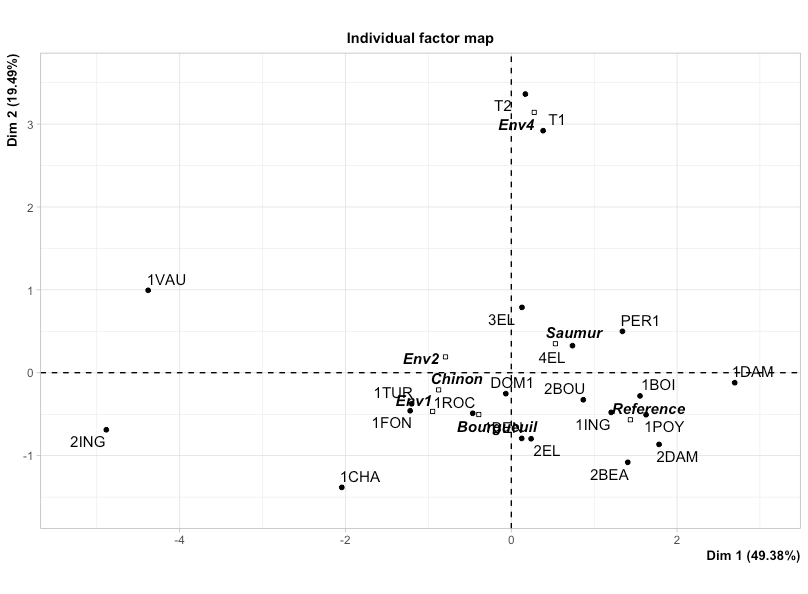
それぞれのワインの相対的な位置に加え、num.group.supで指定したラベルの相対関係も表示されています。どのワインとどのワインが似ている、といったことが考察できます。

MFAによる次元削減後の座標

MFAを適用した後の座標は以下のようにして得られます。

res.mfa$ind$coord

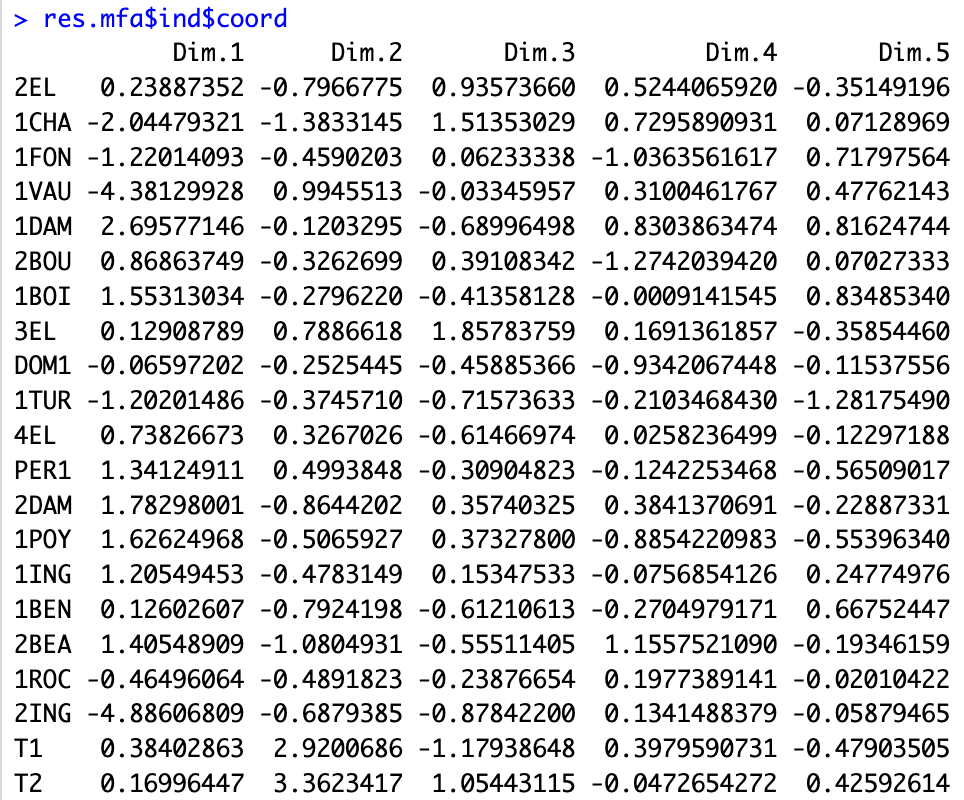
これらの座標は他の次元削減手法と同じように用いることができます。

MFAの軸と各ブロックの関係

以下では2次元に投射したときにの軸とブロックの相関関係を示しています。

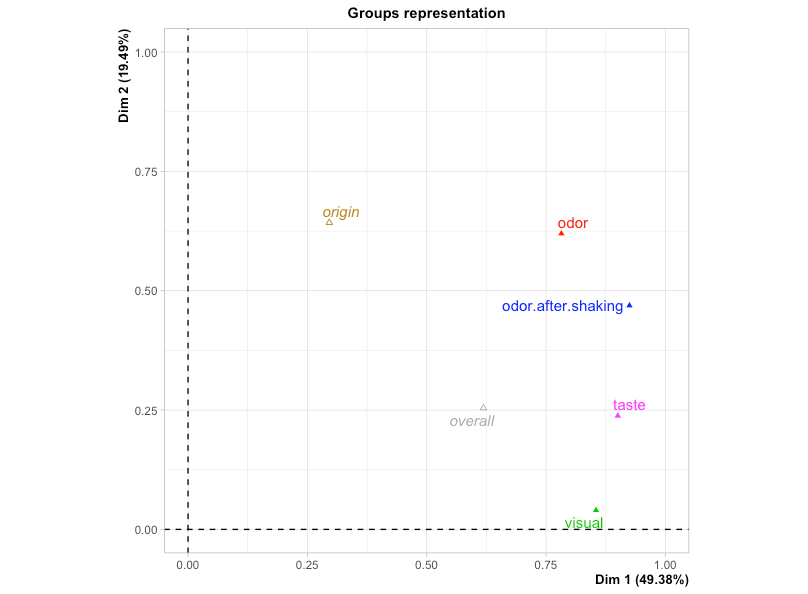
上図より、

第1軸には全てのブロックがほぼ同等に寄与している
第2軸には香りが大きく寄与している

と考察ができます。

PCAの部分軸とMFAの主軸との関係を示した図もあり、

全てのブロックの第1軸がMFAの第1軸とおおよそ同じ方向を向いている = 第1軸には全てのブロックがほぼ同等に寄与している
香り系と味のブロックの第2軸はMFAの第2軸とおおよそ同じ方向を向いている = 香り系と味のブロックが第2軸へ寄与している
味のブロックよりも香り系のブロックのほうが矢印が長い = 香り系のブロックの第2軸への寄与が大きい

と、先程の図と同じような結論が得られます。

これらの図を出せるのはMFAならではですね。

MFAの軸と各変数の関係

以下は個別の変数がどう寄与しているかの図です。

これを見ることで、

それぞれのブロックの中でも特にどの項目が、どの方向に強い寄与をしていたのか = それぞれの軸が具体的にどういう特徴を表現しているのか
どの項目とどの項目が似たような要素なのか

を考察できます。パッと見たところだと

第1軸は◯◯intensityが大きく寄与→ワインの「強さ」のようなもの？
第2軸はSpiceやAcidityなど、「クセ」のようなもの？

を表現しているのかなと考えられます。(ワインに詳しくないのでよくわからないこと言っているかもしれませんが)

このプロットと最初のプロットを合わせて眺めることで、

1DAMや1BOIは力強い銘柄なのだろう
T1やT2は辛い銘柄なのだろう
Env4の土壌は辛味への影響が強そうだ
一般にソミュール産は力強く、ブルグイユ産は優しく、シノン産は個性の強さが特徴なのだろうか

のような考察ができます。

各ブロックと各変数の関係

以下のプロットではそれぞれのラベルが各ブロックのPCAではどの位置にいたかを示しています。

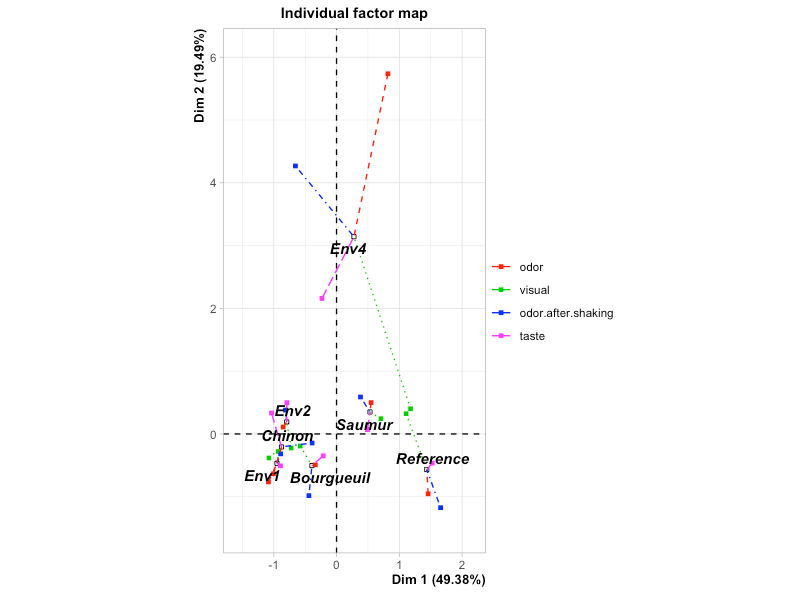
最後の1枚ではそれぞれの銘柄がそれぞれのブロックの軸ではどの位置にいたかをを示しているのですが、自動では一部の銘柄の点しか表示してくれません。「どの銘柄・ラベルに着目して」というのを指示してプロットすべきです。
追加でfactoextraというパッケージも用い、以下のコードで任意の銘柄の各ブロックの軸での位置を表示できます。

install.packages("factoextra")
library(factoextra)
fviz_mfa_ind(res.mfa, partial = c("1DAM", "1VAU", "2ING"))

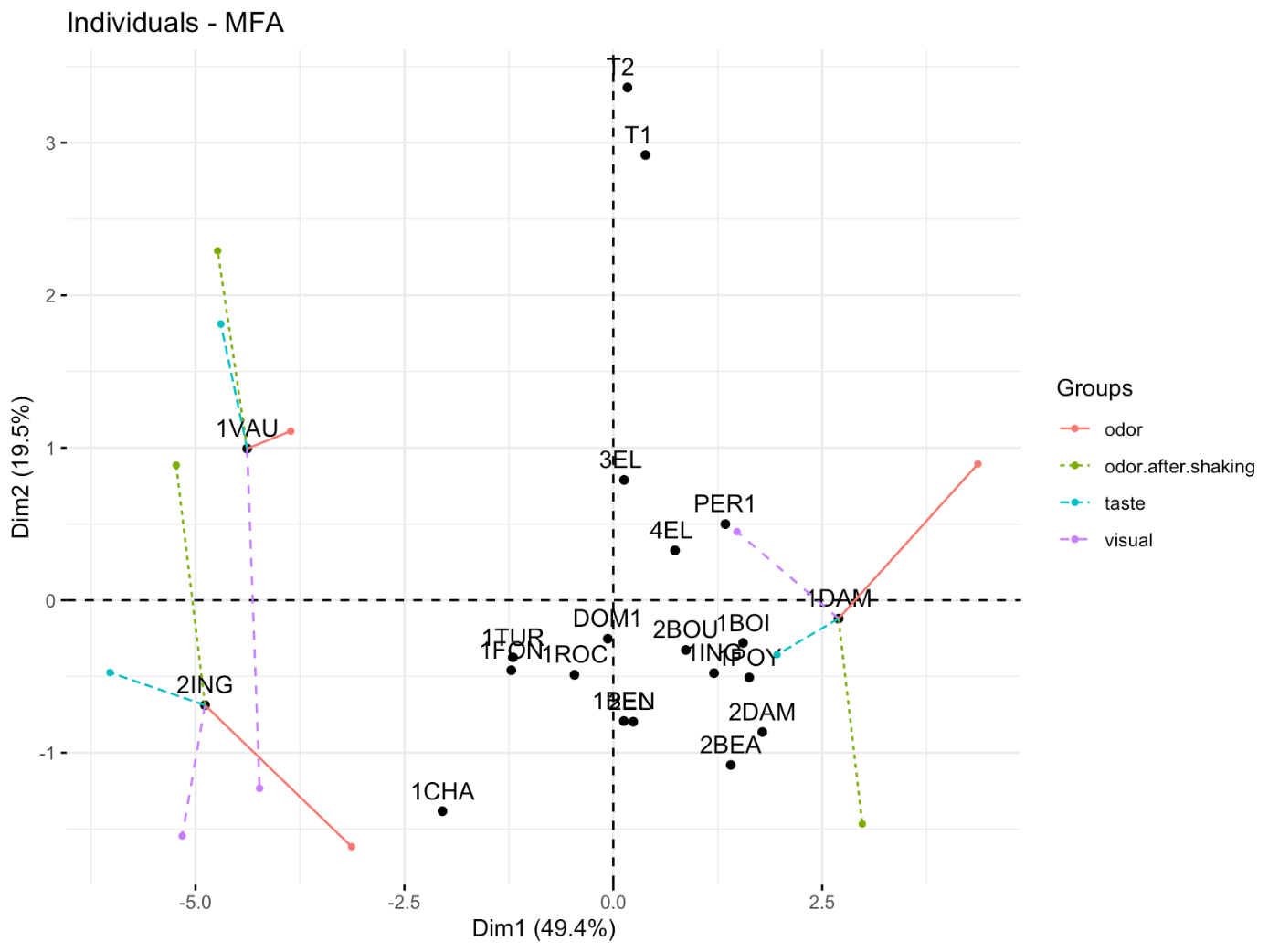
これを見ると、

スワリング前の香りの観点 (赤) から見ると2INGは1VAUよりも力強い (第1軸の座標が右にある) が、味 (青) の観点からは1VAU の方が力強い

といった考察ができます。個別銘柄の特徴みたいなものまで見えてきましたね。これらの図示・考察もMFAだからできることになります。

おわりに

本稿ではMFAを用いた質的に異なるデータの統合分析方法の一例をお示ししました。この方法を使うことで大きく性質の異なるデータや、取得できる項目が異なってしまったデータであってもバランスを取って分析・解釈することが可能になります。

また、データの解釈目的のみでなく、次元削減を目的とした活用も非常に有用です。昨今は「高次元データにはとりあえずt-SNE」のような流れがある一方で、先に述べたように恣意性が高いと批判もあります。
MFAは解釈性・妥当性の高い線形次元削減の有力な選択肢の一つとして、今後更に脚光を浴びていくのではないでしょうか。

本稿がみなさまのデータ分析のお役に立てば幸いです。

参考文献

Abdi, Hervé, et al. “Multiple Factor Analysis: Principal Component Analysis for Multitable and Multiblock Data Sets.” Wiley Interdisciplinary Reviews. Computational Statistics, vol. 5, no. 2, Mar. 2013, pp. 149–79. https://wires.onlinelibrary.wiley.com/doi/10.1002/wics.1246
Principal Component Methods in R: Practical Guide | MFA - Multiple Factor Analysis in R: Essentials http://www.sthda.com/english/articles/31-principal-component-methods-in-r-practical-guide/116-mfa-multiple-factor-analysis-in-r-essentials/

脚注

Abdi et al., 2013のFigure 1が分かりやすい。ブログでの図の引用がライセンス的に微妙なので、アクセスできる方は見てみて下さい。https://wires.onlinelibrary.wiley.com/doi/10.1002/wics.1246 ↩︎
KernelPCAなど非線形の処理を挟んだ場合を除く。 ↩︎
非線形次元削減法から恣意性を除こうという取り組みもあります。https://zenn.dev/aidemy/articles/11f3c0deef923c ↩︎
データのクオリティ・信頼度という意味での "質" はまた別の話です。ランダム割付が適切に行えているか、ブラインドテストが達成できているか、等。データの信頼度が担保できていないのであれば、何をしても強い結論は導き出せません。 ↩︎
カテゴリカル変数に対してはPCAではなくMultiple Correspondence Analysis: MCAが適用されます。 ↩︎
PythonにはPrinceというMFAを実行するパッケージがありますが、本稿執筆時点では行える分析が限られています。scikit-learnを用いて根性で実装することも可能ですが、そこまでやるなら (実装に興味がある人以外は) Rを使った方が良いかなと思います。 ↩︎
データでは "shaking" と表現されていますが、文脈からスワリングのことと勝手に解釈。実務の分析では勝手な解釈はご法度で、言葉の定義は必ず確認しましょう。 ↩︎
ラベルで色分けしたかったり、ある軸に着目して寄与の大小を比較したかったりといった発展的な可視化方法は参考文献の2つ目が詳しいです。 ↩︎

Aidemy Tech BlogPublication

株式会社アイデミーの技術ブログです。