🐷

最小二乗法と仲良くなりたい③

2024/06/04に公開

統計

最小二乗法

線型回帰

tech

3行まとめ

誤差の分布を正規分布だと仮定することで推定量の分布形状を議論できる
推定量の分布形状を議論することで、推定量に関する検定が実施できる
スクラッチで単回帰の推定量導出から検定まで実施してみました

今回は

前回の記事では、最小二乗法によって推定される係数（＝最小二乗推定量）の期待値と分散を計算することで、不偏性と一致性を満たすことを証明しました。
これによって最小二乗推定量は有用な点推定量だと見做せる一方で、そのばらつきによっては、今回の実験データから得られた推定量が（本来は小さいのにも関わらず）たまたま大きかったのかもしれませんし、得られるべくして大きい値が得られたのかもしれません。
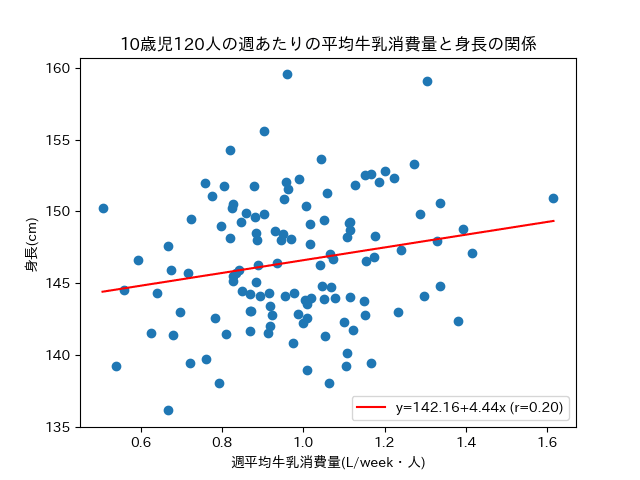
例えば、前々回に例として出した牛乳と背丈の関係でいえば、牛乳摂取量にかかる係数である $\beta_2$ について、最小二乗法で算出した推定量( $\hat{\beta_2}_{OLS}$ )では4.44だったけど、たまたま今回のサンプルが良かっただけで本当(つまり真の $\beta_2$ )は効果は0ってことがあるのかないのか？という心配が残るわけです。
今回はここについて、誤差項にさらに仮定を敷きつつ検討して行きたいと思います。

参考書籍

引き続き統計学入門 a.k.a 赤本の範疇の内容でございますー。

方針

得られたデータがたまたまだったのか、なるべくしてそうなったのかを、(頻度主義的)統計学に則って議論するための手法といえば、統計的仮説検定ですね。

統計的仮説検定は、ある気になっている事柄に対してあって欲しい結論を否定するような帰無仮説をたて、あらかじめ設定した閾値（有意水準）を元に帰無仮説の確率的な尤もらしさを評価し、帰無仮説が棄却できればあって欲しい結論を採択することができる、という取り組みです。
そして検定を実施する際に、気になっている事柄の背後にパラメトリックな確率分布を仮定する検定をパラメトリック検定、確率分布を仮定しない検定をノンパラメトリック検定と呼びます。

今回であれば、気になっている事象は $Y_i = \beta_1 + \beta_2X_i + \epsilon_i$ の $\beta_2$ であって、あって欲しい結論は「 $X$ は $Y$ に対して何かしら影響を持つこと」、それを否定する帰無仮説は「 $\beta_2 = 0$ 」となります^[1]。

この $\beta_2$ について、 $\beta_2 = 0$ を帰無仮説にした検定に持ち込むことを考えて行きましょう。

現時点でわかっていること

「 $\beta_2$ を検定する」と意気込んだところで、我々が今 $\beta_2$ についてわかっているのは、最小二乗法を使って推定した、 $\hat{\beta_2}_{OLS}$ とその分散と期待値です。

\begin{align*} \hat{\beta_2}_{OLS} &= \frac{Cov(XY)}{V(X)} \\ E(\hat{\beta_2}) &= \beta_2\\ V(\hat{\beta_2}) &= \frac{\sigma^2}{\sum_{i=1}^{n} (X_i-\bar{X})^2}\\ \end{align*}

ここから検定、特にパラメトリック検定に持ち込むために、 $\hat{\beta_2}_{OLS}$ を確率変数たらしめている確率変数 $\epsilon_i$ の分布形状に仮定を敷いて、 $\hat{\beta_2}_{OLS}$ の分布形状を考えてみたいと思います。

これまでの仮定と追加の仮定

これまでの議論の中では、確率変数である誤差 $\epsilon_i$ については平均と分散に関する仮定を3つ敷いたものの、その分布の形状については特に仮定を敷いていませんでした。

仮定①：誤差 $\epsilon_i$ の期待値は0であるものとする
仮定②：誤差の分散は常に一定である $\dotsi V(\epsilon_i) = \sigma^2$
仮定③：誤差間に相関はないものとする $\dotsi Cov(\epsilon_i, \epsilon_j)=0$

今回、 $\hat{\beta_2}_{OLS}$ の分布形状を定めるために、 $\epsilon_i$ がパラメトリックな確率分布に従っているという仮定を立てたいと思います。
そして、ちょっとずるい気もしますが^[2]、一般的に測定誤差は中心極限定理により正規分布に従うことが知られる、ということを使って、以下のように仮定を敷くことにします。

仮定④：誤差 $\epsilon_i$ は正規分布に従う

これまでの仮定と組み合わせると、誤差 $\epsilon_i$ は、平均 $\mu$ 、分散 $\sigma^2$ の正規分布から得られる確率変数であると表現することができます(というか、この表現で仮定①〜④をすべて表現することができますね)。

\epsilon_i \sim \mathit{Normal}(0,\sigma^2)

この仮定を元にすると、 $\epsilon_i$ の線型式で表される $\hat{\beta_2}_{OLS}$ もまた正規分布に従うことになり、期待値と分散は導出しているので、以下のように書き下すことが可能になります。

\hat{\beta_2}_{OLS} \sim \mathit{Normal}(\beta_2,\frac{\sigma^2}{\sum_{i=1}^{n} (X_i-\bar{X})^2})

$\sigma^2$ をどうしよう

$\hat{\beta_2}_{OLS}$ の標本分布もわかったことだし、と検定に進もうと思っても、立ちはだかるのは $\sigma^2$ ・・・
ということで、 $\sigma^2$ について考えてみましょう。

そもそも、 $\sigma^2$ は、 $\epsilon_i$ の真の分散として仮定した値でした。
真の値は神のみぞ知る値なので、我々人間ができることは推定、でしたね。
推定するときは不偏性と一致性を満たしていてほしい、でしたね。
母分散の点推定量としてふさわしいのは不偏分散、でしたね。

ということで、真の $\epsilon_i$ の分散 $\sigma^2$ を推定するために、今得られているサンプルから誤差の標本不偏分散を求めて行きます。

\begin{align*} error_i (=e_i) &= Y_i - \hat{Y_i} \\ &= Y_i - (\hat{\beta_1}_{OLS} + \hat{\beta_2}_{OLS} X_i) \\ s^2 &= \frac{\sum{(e_i - \bar{e})^2}}{dof} \end{align*}

ここで、一旦振り返りましょう。
そもそも最小二乗法を使って $\hat{\beta_1}_{OLS}$ と $\hat{\beta_2}_{OLS}$ を求める際、この $e_i$ の二乗和( $SSR$ )が最小になるように、ということで2つの偏微分方程式を立てました。
細かい導出は過去記事に戻っていただくとして、以下に整えた連立方程式を再掲します。

\begin{align} \dfrac{\partial}{\partial \beta_1} SSR(\beta_1,\beta_2) &= \sum_{i=1}^{n} e_i &= 0 \\ \dfrac{\partial}{\partial \beta_2} SSR(\beta_1,\beta_2) &= \sum_{i=1}^{n} X_ie_i &= 0 \\ \end{align}

これによって、 $e$ の標本平均 $\bar{e}$ は0であり、 $e_i$ は $(1)$ 、 $(2)$ の2つの制約を持っているため自由度 $dof$ は $n-2$ となり、誤差項の標本不偏分散 $s^2$ と、そこから求められる $\hat{\beta_2}_{OLS}$ の不偏分散を以下のように表すことができます。

s^2 = \frac{\sum{e_i^2}}{n-2} \\ s.e.(\hat{\beta_2}_{OLS})^2 = \frac{s^2}{\sum_{i=1}^{n} (X_i-\bar{X})^2}

ここで $s.e.$ は標準誤差(standard error)であり、推定値の標準偏差を示します。
このブログではまだ取り扱っていませんが、正規母集団を仮定した確率変数を期待値と標本不偏分散で標準化(と同じような計算)をした値がt統計量と呼ばれ、不偏分散と同じ自由度のt分布に従うことが一般的に知られています。

\begin{align*} t &= \frac{\hat{\beta_2}_{OLS} - E(\hat{\beta_2}_{OLS})}{\sqrt{u^2}} \\ &= \frac{\hat{\beta_2}_{OLS} - \beta_2}{s.e.(\hat{\beta_2}_{OLS})} \sim t(dof)\\ \end{align*}

t検定を実施

ここまできたらほとんどゴールですね。
帰無仮説 $\beta_2 = 0$ を代入したt統計量を計算し、t分布表からあらかじめ設定したパーセント点( $t_{\alpha/2}(n-2)$ )を求め、t統計量の絶対値がパーセント点よりも大きければ帰無仮説が真とすると今回得たt統計量が得られる確率が有意水準未満なので、統計学的に帰無仮説を棄却し対立仮説を採択するのが妥当である、というジャッジを下します。

また、設定したパーセント点を用いて、以下のように不等式を設定し、 $\beta_2$ について解くことで、 $\beta_2$ の区間推定も実施することができます。
この推定区間に0を含まないということと、検定で帰無仮説 $\beta_2 = 0$ を棄却できるということは同値ですね。

\begin{gather*} -t_{\alpha/2}(n-2) &<& t &<& t_{\alpha/2}(n-2) \\ -t_{\alpha/2}(n-2) &<& \frac{\hat{\beta_2}_{OLS} - \beta_2}{s.e.(\hat{\beta_2}_{OLS})} &<& t_{\alpha/2}(n-2) \\ \hat{\beta_2}_{OLS} - t_{\alpha/2}(n-2) \cdot s.e.(\hat{\beta_2}_{OLS}) &<& \beta_2 &<& \hat{\beta_2}_{OLS} + t_{\alpha/2}(n-2) \cdot s.e.(\hat{\beta_2}_{OLS}) \end{gather*}

牛乳摂取量と身長のデータから実際に計算してみる

もちろん、Rにせよpythonにせよ、サクッと最小二乗推定を行なって検定までしてくれるライブラリはありますが、今回は勉強のために実際に計算してみます。

コードに関して

以下、実験や製図に使用したコードをトグルにて記述します。
python3.10.11でjupyter notebook上で実施していますが、大したコードではないので細かいパッケージのバージョン情報は割愛します。
また、すべて冒頭で以下のパッケージ、ライブラリをインポートしていることが前提で記載しています。

前々回に使ったダミーデータを使います(欲しい人などいないと思いますが、一応データはgithubにあります)。
散布図

コード

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import scipy.stats as stats

# データフレームをdfとして読み込んだところからスタートします。

# x,yを設定
x = df.milk
y = df.height
# xの分散と共分散を算出
v_x, cov_xy = np.cov(x,y,ddof=0)[0]
# OLS推定量を算出
beta_2 = cov_xy/v_x
beta_1 = np.mean(y) - beta_2*np.mean(x)
# yの推定値から標本誤差を求め、OLS推定量の標準誤差を算出
y_hat = beta_1 + beta_2 * x
error = y_hat - y
s_2 = np.var(error,ddof=2)
se_beta_2 = np.sqrt(s_2/np.sum(np.power(x-np.mean(x),2)))
# t検定量を算出
t = beta_2/se_beta_2
dof = len(x)-2

x_t = np.linspace(-5,5,1000)
y_t = stats.t.pdf(x_t,dof)
p = 0.05
upper_limit = stats.t.ppf(q=1-p/2,df = dof)

plt.plot(x_t,y_t,c='gray',label = 'pdf')
plt.vlines(ymin=0,ymax=np.max(y_t),x=upper_limit,linestyles='--',color='red',label='significant level')
plt.vlines(ymin=0,ymax=np.max(y_t),x=-upper_limit,linestyles='--',color='red')
plt.fill_between(x_t,y_t,where=x_t<-upper_limit,facecolor='red',alpha=.5,label = f'reject area(p<.05)')
plt.fill_between(x_t,y_t,where=x_t>upper_limit,facecolor='red',alpha=.5)

plt.vlines(ymin=0,ymax=np.max(y_t),x=t,linestyles='-',color='c',label='t_value')

plt.title(f't distribution(dof = {dof})')
plt.legend(
    loc='upper left',
    bbox_to_anchor=(1, 1),
    ncol=1,
    )

beta_bottom = beta_2 - upper_limit*se_beta_2
beta_top = beta_2 + upper_limit*se_beta_2

print(f'beta_2の95%信頼区間は{beta_bottom:.3f}~{beta_top:.3f}')

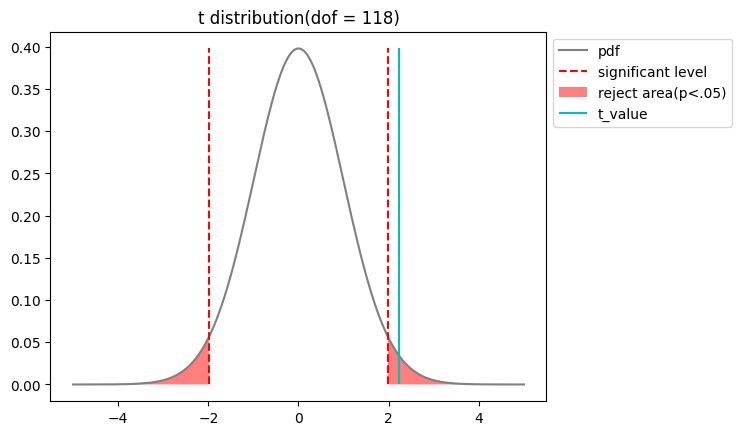
alt text
以上の結果から、有意水準5%においては $beta_2$ は非ゼロだと考えて良さそうであり、推定値は4.438、95％信頼区間は0.492~8.384だ、というように推定ができました。

終わりに

今回はあくまで単回帰というシンプルなケースを例に証明や導出を行なってきましたが、変数が複数個になる重回帰分析においても基本的には同じような考え方で検討することになります。
実際の分析においては単回帰を使うケースはあまりないように思います...関係がありそうな変数(共変量)もデータを入手しておいて、交互作用を考えたりドメイン知識から変数選択をしたり、RidgeやLassoなどの正則化を用いた変数選択のテクニックを使ったり、ということをしながら重回帰分析をしていく感じですかね。
実は重回帰分析やベイズ線型回帰にも使えるかと思って、今回のデータセット作成においては、身長に効く共変量として親の身長や運動習慣などを入れ込んでいたのですが、一旦最小二乗法についてはここで区切りとしたいと思います。

本当はベイズ線型回帰についてもまとめたいなーと思いつつ・・・

以上、ご確認のほど、よろしくお願いいたします。

脚注

今回は負の作用がないとも限らない、という立場に立って両側検定を行います。対立仮説は $\beta_2 \neq 0$ です。帰無仮説が棄却できれば、 $\beta_2$ は非ゼロ、つまり $X$ は $Y$ に対して何かしら影響を持つことが示唆され、得られた推定量が正の値であれば結果として、 $X$ は $Y$ に対して正の影響を及ぼすと推定できる、というステップになります。場合によっては、「 $X$ は $Y$ に対して負の影響が起こることはないのである」という前提に立って、対立仮説を $\beta_2 > 0$ と設定することもありますが、個人的にはロジックがない限り片側検定はちょっと怪しい気がしてしまいます・・・ ↩︎
何か測定器具で測るようなことに対する測定誤差については正規分布でもっともらしいように思うのですが、今回の例で言えば、例えば身長を牛乳摂取量で回帰した時に、牛乳摂取量だけでは表しきれない特徴が全て誤差として表現されてしまいます。例えば、月齢とか、運動習慣とか、それらの交互作用とか。中心極限定理を背景として誤差を正規分布と仮定している以上、誤差の構成要素は類似した母集団分布に従う独立な確率変数である必要があります。しかしながら、回帰する上で重要な説明変数が抜け落ちていたりすると、中心極限定理を導入するための仮定が成り立たないことになってしまったりします。 ↩︎

GitHubで編集を提案