最小二乗法と仲良くなりたい①

3行まとめ

1. 最小二乗法は残差平方和(誤差の二乗和)が最小となる回帰式を求める手法。
2. 簡単のために変数が1つのケースを具体例として最小二乗法で回帰式を求めてみる。
3. 最小二乗法で推定した係数は推定量として適切なのかが気になってくる。

きっかけ

きちんと統計学を勉強したい、というモチベーションで、赤本 → 緑本と進み、現在は*標準とは？*で有名な標準ベイズ統計学を読み進めているところ…なのですが、線型回帰の章に入って「オレは何も最小二乗法のことをわかってなかった…」と痛感するばかりの日々を送っています^[1]。
というわけで、今回からは、単変量の最小二乗法、いわゆる単回帰を取り上げて反芻していきたいと思います。

参考書籍

上述の通り、きっかけは標準ベイズですが、今回はいわゆる頻度論的な解釈で復習したいと思いますので、入門詐欺本として名高い統計学入門 a.k.a 赤本 の範疇の内容になります。

免責事項
間違いのないように理解したいという思いで学習をしていますが、なにぶん独学であり、専門ではありませんので、あくまでも私はこう解釈した、という内容であることご了承ください。
本文において断定調で記載している部分もありますが、いちいち「〜と私は理解しています」と記載すると冗長になってしまうので、体裁上「〜です」と記載しています。
決定的な誤りや、危険な解釈をしていると思われた場合は忌憚なくご指摘いただけますと幸いです。

序文 : 点の中に線を引くのってキモチイイ

最小二乗法って、人間の本能にとてもよくマッチした推定方法だと感じています(個人の感想です)。
ほら、子供の頃から点を結んで絵を作るやる、アホほどやるじゃないですか？
点を見つけると線を引きたくなるのって、人間の本能だと思うんですよね。

もちろんアカデミアだったり、企業研究者だってちゃんとリテラシを持った人であればそんなことはないとは思いますが、私の前職とかだと、ブワァっとある点の集合にもっともらしい線が引かれて、小数点以下４桁とかの数値を出して「ゆるい相関があります」とかっていうのが横行するわけです。
エクセルでグラフを書いてちょちょいのちょい、とすると、モットモらしい線とモットモらしい式が出てくるんでね、なんかすごく頭がいいことを言っているような気になるんですよね^[2]。

そういう観点でモットモらしく線を引く、という行為に対して数学的な妥当性を与えてくれる最小二乗法はすごい発明だなぁ、と勉強するたびに感嘆してしまいます。
そういえば遠い記憶で、大学1年のコンピュータリテラシの授業でも最初に最小二乗法を扱っていた気がします^[3]。

そんな大学時代〜前職での思い出に浸りつつ、真面目に最小二乗法を咀嚼していきたいと思います。

最小二乗法って何してるん？

最小二乗法は、回帰式を求めるための手法の一つです。
回帰というのは、予測したかったり解釈したかったり、といった分析者が興味を持っている数値のデータが$n$個手元にあって($Y_i \; i=1,\dots,n$)、その$n$個それぞれに対して予測や解釈に使えそうな他の数値データも持っている($\bold{X}_i \; i=1,\dots,n$)ようなときに両者の関係を数式で表そうとする取り組みのことを言いました。
そして、両者の関係を表す数式のことを回帰式、と呼ぶのでした。

ただし、どうしたって測定誤差が出てしまうだとか、持っていないデータの中にも重要なデータがあったかも知れない^[4]だとか、回帰式だけでは表現しきれない要素はどうしてもあるよね、ということで、それをまるっと誤差項($\epsilon_i$)として、以下のように表すことにします。

$$Y_i=f(\bold{X}_i) + \epsilon_i \quad \footnotesize (i=1,\dots,n)$$

最小二乗法は、一言で言ってしまえば、n個のデータの誤差項の合計が最も小さくなるような回帰式を求めよう、というコンセプトです。
とはいえ誤差はプラスだったりマイナスだったりして、単純に合計を取るとお互いに打ち消しあってしまうので、符号を無視するために二乗してから足し合わせよう、という工夫をしています。
この誤差の二乗を足し合わせた数のことを、残差平方和(Sum of Squared Residuals;SSR)と呼びます。

$$SSR = \sum_{i=1}^{n} \epsilon_i^2$$

広義でいえば、回帰モデルが線型だろうが非線形だろうが関係なく、残差平方和を最小にするような回帰式を求めることが最小二乗法の定義になります。
ただし、一般的には回帰式が線型で表される(と仮定できる)ときに最小二乗法を適応するケースがほとんどかと思います。
これは線型回帰を仮定すると残差平方和が$\beta_i$の二次関数となるため、$\beta_i$で微分した導関数が0になる時、残差平方和が極少となる、ということを導くことができるからです。

$$f(\bold{X}_i) = \boldsymbol{\beta}^\mathsf{T}\bold{X}_i = \beta_1X_{i1} + \beta_2X_{i2} + \dotsc + \beta_pX_{ip} \\ SSR(\boldsymbol{\beta}) = \sum_{i=1}^{n} \epsilon_i^2(\boldsymbol{\beta}) = \sum_{i=1}^{n} (Y_i - \boldsymbol{\beta}^\mathsf{T}\bold{X}_i)^2 \\ \frac{d}{d\boldsymbol{\beta}} SSR(\boldsymbol{\beta})=0 \to \min SSR(\boldsymbol{\beta})$$

この時の回帰式やそれによって描かれる直線を回帰直線^[5]、回帰式の係数である$\boldsymbol{\beta}$を回帰係数と言ったりします。

一般的には定数項の導入するために、$X_{i1}=1$とすることが多いかと思います。
これはいわゆるy軸切片でして、「必ずしもこの$\bold{X},Y$のグラフは原点を通るとは限らない」ということを表現しています。
これに倣い、以降も$X_{i1}=1$として進めていきます。

具体例で考える

これからの議論で使うことができる、ちょっとした例を考えてみましょう。
まずは単純に、$p=2$、つまり変数$\bold{X_i}$の要素が定数項1の他に1つだけのときの、単回帰について考えます。

<例>
牛乳メーカーのマーケティング担当者が、「牛乳をしっかり飲ませて子供の背を伸ばしましょう」みたいなキャンペーンを打ちたいので、子供の身長と1週間あたりの牛乳の摂取量の関係を知りたい、と思ったとしましょう。
その関係を見つけるために、10歳児をランダムに$i$人集めてきて、それぞれの身長と、1週間あたりの平均牛乳摂取量を調査したとします。

このとき、興味の対象は子供の身長であって、$Y_i = i$人目の子供の身長、$X_i = i$人目の子供の牛乳摂取量という対応になります。
そして「身長と牛乳摂取量は比例関係にあるはず」という仮説から$Y_i = \beta_1 + \beta_2 X_i + \epsilon_i$という式を立て、手持ちの$i$人分の観測値を使って、

$$SSR(\beta_1,\beta_2) = \sum_{i=1}^{n} (Y_i - \beta_1 - \beta_2 X_i)^2 \\ \begin{align*} \left\{ \begin{align*} & \dfrac{\partial}{\partial \beta_1} SSR(\beta_1,\beta_2)= 0 &\\ & \dfrac{\partial}{\partial \beta_2} SSR(\beta_1,\beta_2)= 0 &\\ \end{align*} \right. \end{align*}$$

導出過程

$$\begin{align*} \dfrac{\partial}{\partial \beta_1} SSR(\beta_1,\beta_2) &= \sum_{i=1}^{n} -2(Y_i - \beta_1 - \beta_2 X_i) \\ &= 2n\beta_1 + 2\beta_2 \sum_{i=1}^{n}X_i - 2\sum_{i=1}^{n}Y_i \\ &= 2n (\beta_1 + \beta_2 \bar{X} - \bar{Y}) \\ \dfrac{\partial}{\partial \beta_2} SSR(\beta_1,\beta_2) &= \sum_{i=1}^{n} -2X_i(Y_i - \beta_1 - \beta_2 X_i) \\ &= 2\beta_1\sum_{i=1}^{n}X_i + 2\beta_2 \sum_{i=1}^{n}X_i^2 - 2\sum_{i=1}^{n}X_iY_i \\ &= 2n (\beta_1\bar{X} + \beta_2 \bar{X^2} - \bar{XY}) \\ \end{align*}$$

より、

$$\begin{align*} \left\{ \begin{align} & \hat{\beta_1} + \hat{\beta_2} \bar{X} - \bar{Y}= 0 &\\ & \hat{\beta_1}\bar{X} + \hat{\beta_2} \bar{X^2} - \bar{XY}= 0 &\\ \end{align} \right. \end{align*} \\ \begin{align*} (1)から&\hat{\beta_1} = \bar{Y} - \hat{\beta_2} \bar{X} \\ (2) - \bar{X} (1)から&\hat{\beta_2} = \frac{\bar{XY} - \bar{X}\bar{Y}}{\bar{X^2} - \bar{X}^2} \end{align*}$$

ここで$\hat{\beta_2}$について、標本分散と標本共分散の定義

$$\begin{align*} V(X) &= \frac{\sum_{i=1}^{n} (X-\bar{X})^2}{n} = \bar{X^2} - \bar{X}^2 \\ Cov(XY) &= \frac{\sum_{i=1}^{n} (X-\bar{X})(Y-\bar{Y})}{n} = \bar{XY} - \bar{X}\bar{Y} \\ \end{align*}$$

を代入することで以下を得る。

$$\begin{align*} \hat{\beta_2} &= \frac{\bar{XY} - \bar{X}\bar{Y}}{\bar{X^2} - \bar{X}^2} \\ &= \frac{\sum_{i=1}^{n} (X_i-\bar{X})(Y_i-\bar{Y})}{\sum_{i=1}^{n} (X_i-\bar{X})^2} \\ &= \frac{Cov(XY)}{V(X)} \\ \hat{\beta_1} &= \bar{Y} - \hat{\beta_2} \bar{X} \end{align*}$$

を解いて$\hat{\beta_1}$と$\hat{\beta_2}$^[6]を求めていきます。

さて、今回は120人の10歳児に協力をしてもらってデータを集めて(つまり$i=120$)、頑張って上記の計算をして、以下のような結果を得ました(ダミーデータです)。

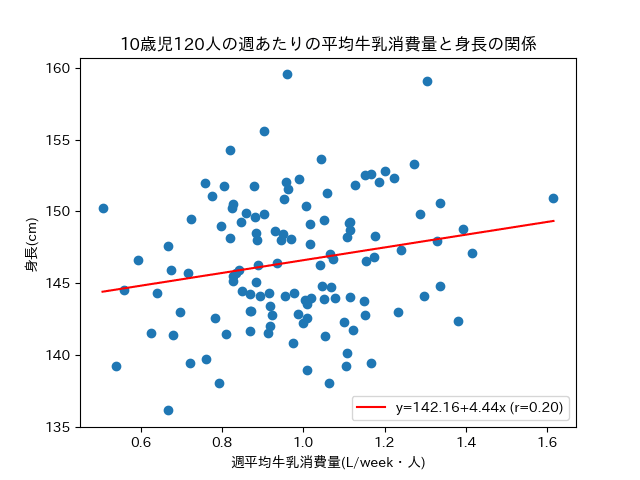
相関係数は0.2で、弱いながらも相関はありそうですね。
ところで、今算出した$\hat{\beta_1}$と$\hat{\beta_2}$は、たまたま調査で得られた120人分のデータから計算した値です。つまり神様が決めた真実の$\beta_1$、$\beta_2$を点推定するための推定量^[7]、と言うことですね。

そうなると、前回議論した、点推定が満たしておいてほしい2つの性質、一致性と不偏性が気になってきます。もしも不偏性や一致性を満たしていなかったら、どんなにサンプルを増やしても、どれだけ調査を繰り返しても、真の$\beta_1$、$\beta_2$を推定することができなくなってしまうので困ってしまいます。

次回からはこのデータを使ってもう少し上記の点を考えていきたいと思います。

終わりに

線型回帰って、点の中にうまく線を引く、と言うとっつきやすいイメージで理解した気になってしまうのですが、知れば知るほどなかなか使えなくなってきてしまいます…
とはいえ「こういう仮定を敷いている」ということをしっかり理解しておくのが大事だと思いますので、備忘のためにアウトプットをさせていただきたく。

以上、ご確認のほど、よろしくお願いいたします。

脚注

1. というか、全般的に「オレは何もわかってなかった…」という感じでございまして、それ自体がこのブログを始めたきっかけだったりします。

2. あくまで私の感想を述べているに過ぎないことにご注意賜りたく。皆々様におかれましてはそんなことあるはずがなかろう！と思われること必至かと思いますので、どこか遠い国のお話だったり、筆者の夢の中のお話だったり、反実仮想の話だと思ってお読みいただければと思います。というか、そうです。

3. 当時は計算機室にずらっと並ぶmacで、ぐるぐると虹色に回るアイコンを見ながら、よくわからないままにmatlabをいじいじしていた記憶です。

4. 厳密にいうとこの誤差項の性質によってこのあと議論する仮定が成り立たなくなったりするのですが、ここでは割愛したく。

5. 回帰"直線"というとxとyのグラフにビシッと真っ直ぐな線が惹かれることを想定するかと思いますが、この線型回帰式の$X_{ip}$には、変数のn乗の値や対数、指数が入り得ることに注意してください。例えば、$y=ax^4+b$は、$(x,y)$平面上ではぐにゃぐにゃした曲線ですが、$(x^4,y)$平面上では直線になりますので、線型回帰だと捉えることができます。

6. 頻度論的な解釈ですが、真の$\beta_1$、$\beta_2$を推定するために手持ちの観測データから計算する推定量として、$\hat{\beta_1}$、$\hat{\beta_2}$と表記しています。

7. 最小二乗法(Ordinary Least Squares)を使って求めた推定量なので、$\hat{\beta_1}$と$\hat{\beta_2}$のことをOLS推定量と言ったりします。