Hit&Blowで学ぶ最適化part2 相互情報量
はじめに
前回記事では、Hit&Blowをテーマにベイズ推定の考え方を追っていき、ランダムな方法と比べて少ない手数(平均5.27手)で数を当てることに成功しました。
一方で、前回記事の最後で触れたように、単純に現時点で最も答えの確率が高い数字を宣言していくという戦略には改善の余地がありそうです。本記事では、より良いHit&Blowの戦略として、相互情報量について扱います。(いきなり相互情報量が出てきたのはなぜかというと、AtCoder Heulistic Contest 030で使えるらしいからです。)
なお、前回記事と同様に、Hit&Blowについては探索木的なアプローチ(シンプルな再帰的探索や、mini-max法的アプローチ)がいくつか見つかります。ベイズ推定や相互情報量には興味がなく、Hit&Blowにのみ興味がある人は、(確率分布を持ち込まず解く方がアプローチとして素直なので)そちらを参照してください。
エントロピーと相互情報量の基礎
Hit&Blowで宣言する数は、直感的には(もしくは経験的には)次のどちらかが良い気がします。
- 正解の可能性が高い数字
- 正解の候補を一気に絞れる数字
「1.正解の可能性が高い数字」については、前回の記事の時点で絞れており(各ターンで残っている数字はすべて同じ確率で正解の可能性がある)、そのなかで「2.正解の候補を一気に絞れる数字」を宣言する戦略が有効だと考えられます。どれぐらい候補を絞れるか、を定量的に表すことができるのがエントロピーと相互情報量です。というわけで、この2単語の説明にしばしお付き合いください。
エントロピー 1
エントロピーは、情報理論においては不確実性や情報量をはかる概念です。(余談:自分は物理化学の文脈でエントロピー
ここで
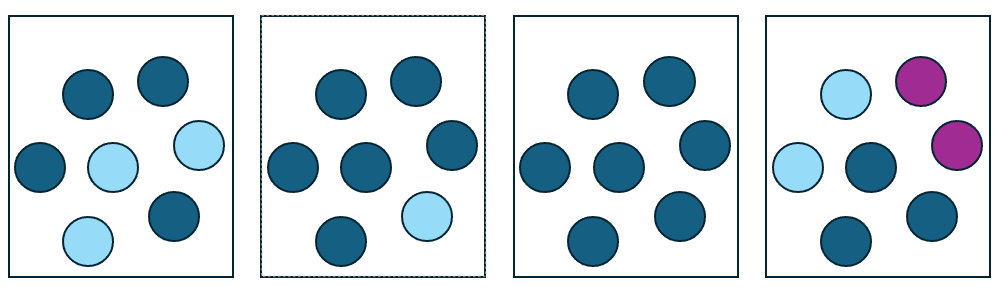
- 左から1番目の箱(青4、水3)
- 左から2番目の箱(青6、水1)
- 左から3番目の箱(青7)
- 左から4番目の箱(青3、水2、紫2)
改めて箱のごちゃごちゃ具合とエントロピーを比較すると、ごちゃごちゃ具合が大きいほどエントロピーが大きくなっていることが分かります。なお、エントロピーの最小値が0であることと、最大になるのは均等に各色があるときであることが示せますが、面倒なのでやりません。
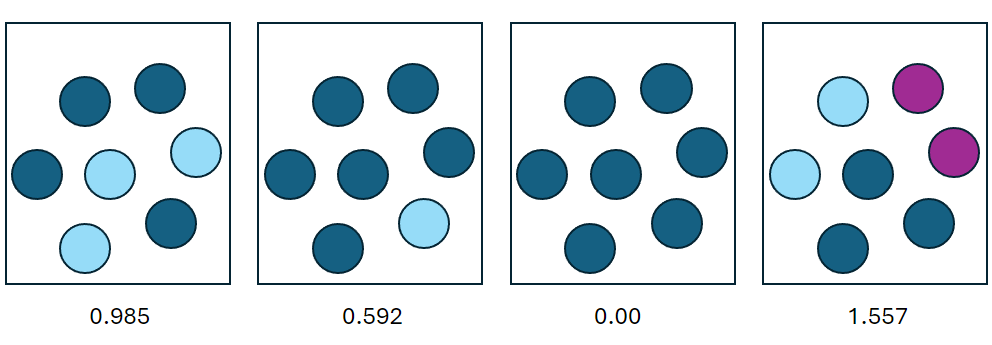
エントロピー 2
ここで少し見方を変えて、ボールではなくて箱そのもののエントロピーを考えてみます。より具体的には、目の前にボールが入った箱が1つあって、その中身は上の4つの中のどれかであることが分かっているとします(どれであるかはわかっていません)。このときのエントロピーは、
と計算できます。いま、箱から1つボールを取り出してその色を確認します。色に応じて目の前の箱が4つの中身のどれであるかを考えることができます。出た色について、それぞれその後の箱のエントロピーを考えてみます。
- 水色の球を引く
この時、目の前の箱は3番目の箱ではないことが分かります。エントロピーは
となり、最初の2からは減りました。
- 青色の球を引く
どの箱である可能性も消えません。エントロピーは
- 紫色の球を引く
一番右の箱で確定します。エントロピーは
これをまとめると次の図になります。
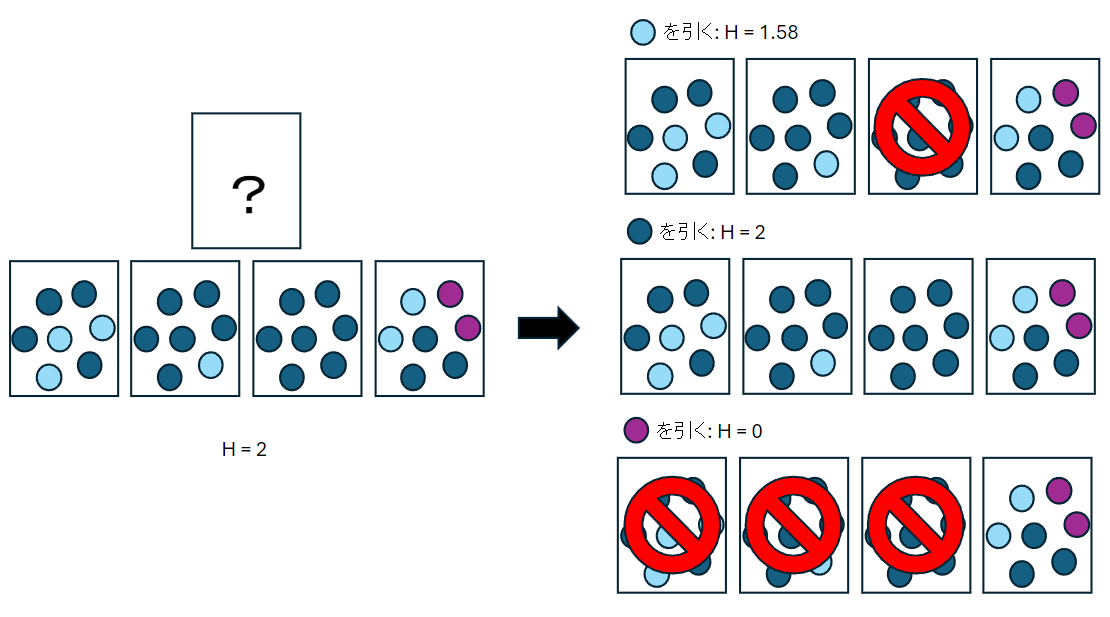
紫色の球を引いた場合は箱が確定し、それ以外でもエントロピーは同じか小さくなりました。球を引き続ければ、(直感通り)どこかのタイミングでエントロピーが
条件付きエントロピー
Hit&Blowも、数を宣言して相手からの結果に合致するもののみを残して後は捨てていくため、上と似た構造です。最終的に答えを1つに絞りたい、つまりエントロピーを0にしたいので、数を宣言して候補を絞った後のエントロピーが0に近ければ近いほど嬉しい感じがします。
相手から結果を聞くまでそれによってどれだけ候補を減らせるか(上の例でいうところの、球が何色に相当するか)が分かりません。そこで期待値を考えることにします。つまり、全ての答えの候補について、0H0Bから3H0Bまでの相手からの結果すべて考え、相手からの結果が
を条件付きエントロピーと言います。
これも式よりも例を見たほうが分かりやすいため、例を考えます。実際のHit&Blowのゲームの1シーンで、012(0H1B)→134(0H2B)と2ターンが経過して答えの候補が残り19個まで絞れている場面を考えます。
このとき、243に対して、残りの候補は次のように分布します。
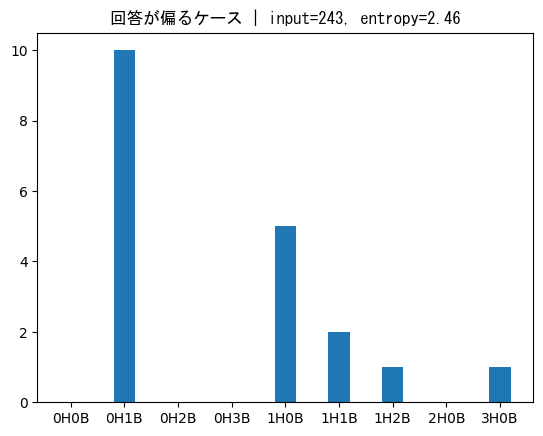
このときの条件付きエントロピーは、
より2.46となります。
一方で、451に対しては、残りの候補は次のように分布します。
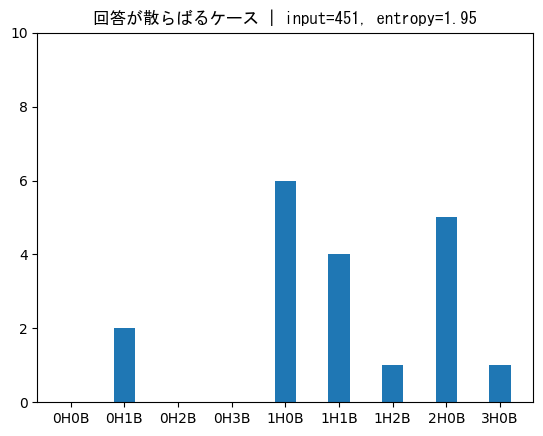
243のときよりも候補が散らばっている感じがします。このときの条件付きエントロピーは、
となり、243のときの2.46よりも小さくなります。
どちらの数字でも3H0Bでクリア、1H2Bが出ても答えを1つに絞れるところは変わりません。違いとして最大値に注目すると、243(前者)の場合は0H1Bが返ってきた場合、次のターンに10個の数の中から絞り込む必要があり大変です。一方で、451(後者)の場合は最大でも次のターンは6個の数の中から絞り込めばよくなります。これは、条件付きエントロピーが小さいほどうまく数を絞っていけることを表しています。
この節でやってきたことをコードに落とし込むだけで、前の記事よりもターン数を縮められそうです。早速実装に移ってもいいのですが、せっかくなのでもう一つ知っておくと便利そうな概念を紹介します。
相互情報量
ある数字を宣言した時にエントロピーが最初の値
前節では条件付きエントロピー
なお、この式のままだと実装のときに少し頭を使います。
せっかく書いたのですが、次の節ではこの式は使わず、
アルゴリズムの実装
ようやく実装の話に入りました。相互情報量を計算し、それに基づいて次の宣言を選ぶアルゴリズムをRustで実装します。前回のコードを拡張し、相互情報量の計算部分を追加します。calc_entropy()からmax_mutual_info()までが新しく追加した部分になります。エントロピーの計算など、事前に計算することで計算時間を短縮することができますが、毎回計算しても大して時間がかからないため、毎回計算しています。(mutual_info()内で
頑張ってコードを読んでください。
#![allow(dead_code, unused_imports, unused_variables)]
use proconio::input_interactive;
use std::collections::HashSet;
use rand::Rng;
fn main() {
let mut rng = rand::thread_rng();
for ans in 0..1000 {
//let ans = gen_answer();
if !is_valid(ans) {
continue;
}
//println!("Answer: {}", ans);
//println!("Please input 3-digit number.");
let judge = Judge::new(ans);
let mut seen_inputs = HashSet::new();
let mut probs = initialize_probs();
normalize(&mut probs);
//ベイズ推定を用いた探索
let mut turn = 0;
loop {
//前の記事と異なる部分
//相互情報量が最大となる数字をinputとして選択
let input = max_mutual_info(&probs);
if seen_inputs.contains(&input) {
panic!("Duplicate input: {}", input);
}
seen_inputs.insert(input);
let (hit, blow) = judge.judge(input);
turn += 1;
//println!("turn {}: input: {}, {} hit, {} blow", turn, input, hit, blow);
if hit == 3 {
//println!("Congratulation!");
break;
}
//ベイズ推定
bayes_update(&mut probs, input, (hit, blow));
}
println!("{}", turn);
}
}
fn initialize_probs() -> Vec<f64> {
let mut probs = vec![0.0; 1000];
for i in 0..1000 {
if is_valid(i) {
probs[i] = 1.0;
}
}
probs
}
fn calc_entropy(probs: &Vec<f64>) -> f64 {
//エントロピーの計算
probs.iter().filter(|p| **p > 0.0).map(|p| -p * p.log2()).sum::<f64>()
}
fn calc_conditional_entropy(probs: &Vec<f64>, input: usize) -> f64 {
//条件付きエントロピーの計算
let mut judge = Judge::new(input);
//results: (hit, blow)
let results = vec![(0, 0), (0, 1), (0, 2), (0, 3), (1, 0), (1, 1), (1, 2), (2, 0), (3, 0)];
let mut weights = vec![0.0; 10];
for x in 0..1000 {
if probs[x] == 0.0 {
continue;
}
let (hit, blow) = judge.judge(x);
for (i, (h, b)) in results.iter().enumerate() {
if hit == *h && blow == *b {
weights[i] += 1.0;
}
}
}
let mut new_probs = weights.clone();
normalize(&mut weights);
let mut hxy = 0.0;
for i in 0..10 {
if weights[i] == 0.0 {
continue;
}
hxy += weights[i] * new_probs[i].log2();
}
hxy
}
fn mutual_info(probs: &Vec<f64>, input: usize) -> f64 {
//相互情報量の計算
let hx = calc_entropy(probs);
let hxy = calc_conditional_entropy(probs, input);
hx - hxy
}
fn max_mutual_info(probs: &Vec<f64>) -> usize {
//相互情報量が最大となる数字を選択
let mut max_mi = 0.0;
let mut max_input = 0;
for i in 0..1000 {
if probs[i] == 0.0 {
continue;
}
let mi = mutual_info(probs, i);
if mi > max_mi {
max_mi = mi;
max_input = i;
}
}
max_input
}
fn normalize(probs: &mut Vec<f64>) {
let sum = probs.iter().sum::<f64>();
assert!(sum > 0.0);
probs.iter_mut().for_each(|x| *x /= sum);
}
fn bayes_update(probs: &mut Vec<f64>, input: usize, (hit, blow): (usize, usize)) {
//尤度の計算
let mut likelihoods = vec![0.0; 1000];
let mut judge = Judge::new(input);
for i in 0..1000 {
if is_valid(i) {
let (h, b) = judge.judge(i);
if h == hit && b == blow {
likelihoods[i] = 1.0;
}
}
}
//事後確率の更新
probs.iter_mut().zip(likelihoods.iter()).for_each(|(x, y)| *x *= y);
normalize(probs);
}
fn gen_answer() -> usize {
let mut rng = rand::thread_rng();
let mut ans = 0;
loop {
ans = rng.gen_range(0..1000);
if is_valid(ans) {
break;
}
}
ans
}
fn is_valid(n: usize) -> bool {
let digits = get_digits(n);
digits[0] != digits[1] && digits[1] != digits[2] && digits[2] != digits[0]
}
fn get_digits(mut n: usize) -> [usize; 3] {
let mut digits = [0; 3];
for i in (0..3).rev() {
digits[i] = n % 10;
n /= 10;
}
digits
}
struct Judge {
answer: [usize; 3],
}
impl Judge {
fn new(ans: usize) -> Self {
Judge { answer: get_digits(ans) }
}
fn judge(&self, input: usize) -> (usize, usize) {
let mut digits = get_digits(input);
let mut hit = 0;
let mut blow = 0;
for (i, &d) in digits.iter().enumerate() {
if self.answer[i] == d {
hit += 1;
} else if self.answer.contains(&d) {
blow += 1;
}
}
(hit, blow)
}
}
パフォーマンス評価
正解となり得る720組それぞれについて、上のコードを実行して答えを当てるまでにかかったターン数(宣言した数)を求めます。平均は5.15で分布は次のようになりました。
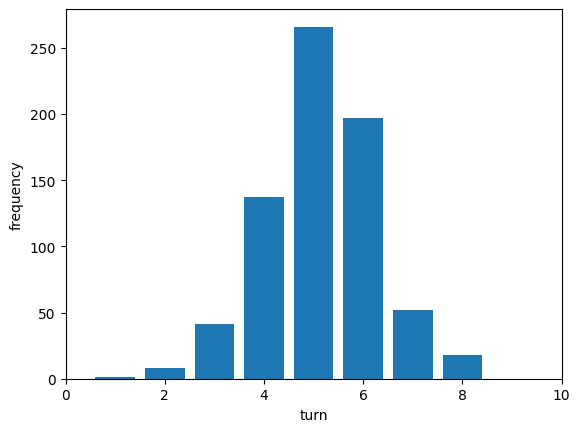
前回記事の平均手数が5.27であったことから、少し改善しています。前回と今回の2つの分布をならべて比較すると次のようになっています。 前回から3、4、5手で当てられる回数が増えて、逆に6、7、8、9手かけて当てていた数字が減っていることが分かります。平均で0.12の違いだとあまり嬉しい感じがしませんが、(当てるのに回数がかかる)苦手な数字が減っているというのは、平均的に強くなっている感じがして頼もしいです。
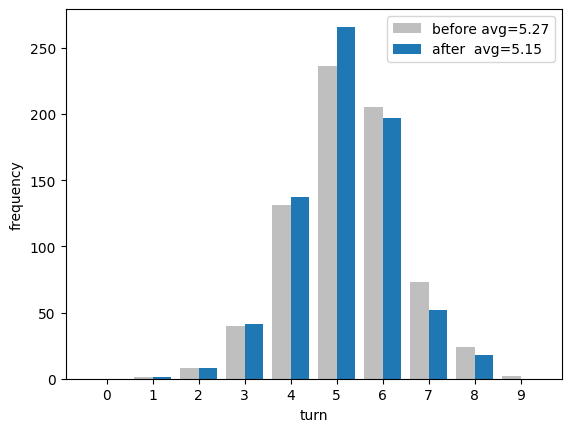
まとめ
本記事では、相互情報量をHit&Blowに適用し、より少ないターン数で数を当てることに成功しました。ベイズの入門と情報理論の入門を組み合わせるだけでこんなことができるなんて驚きです。
Discussion