Hit&Blowで学ぶベイズ推定:理論から実装まで
はじめに
Hit&Blowは、相手が秘密に設定した3桁の数字を当てるシンプルな推理ゲームです。最近の自分は、ベイズ推定のコードを書けるように、また他の題材に応用できるようになれたら嬉しいと思っています。Hit&Blowを題材にベイズ推定について考えてみることで、知識を定着させます。
なお、Hit&Blowについては探索木的なアプローチで最短手数を求める先行研究がいくつか見つかりました。ベイズ推定には興味がなく、Hit&Blowにのみ興味がある人は、(確率分布を持ち込まず解く方がアプローチとして素直なので)そちらを参照してください。
Hit&Blowの説明
Hit&Blowの基本ルールは以下の通りです:
- 出題者が000から999までの3桁の数字を秘密に設定します。
- 回答者はその数字を推測し、3桁の数字を宣言します。
- 出題者は次の基準で結果を伝えます:
- Hit:数字と桁の位置が両方正しい場合
- Blow:数字は正しいが、桁の位置が異なる場合
これを繰り返し、3Hitになるまで続けます。
例えば、正解が「567」で、回答者が「576」と答えた場合、1Hit 2Blowとなります。
ベイズ推定の簡単な説明
ベイズ推定とは、新しい証拠や情報が得られるたびに、ある仮説の確からしさ(確率)を更新していく統計的手法です。ベイズの定理に基づき、事前の知識や信念を、観測されたデータを用いて更新し、より正確な推定を行うことができます。
このように書いてある記事が巷には溢れています。分かったような何も分からないような気持になります。そこで、手を動かしてきちんと理解しようというモチベーションのもとに、この記事を書いています。
ベイズ推定の基礎
ベイズの定理の説明
ベイズの定理は、条件付き確率に関する定理です。しばらくHit&Blowのことは忘れて、式変形にお付き合いください。(式を見たくないよ~という人はこの節を飛ばして、次の節から読んでも大丈夫です。)
ある事象
ここで、
実際に計算する場面では、確率として規格化するため、分母は重要ではない場合が多いです。つまり(4)右辺の分母は気にしなくていいのですが、説明のためにこの形で書きました。
上の式の左辺と右辺を比べることで、とても面白いことが分かります。そうです、左辺は
この書き方でも何が嬉しいのかピンとこない人も一定数いると思います。(自分は最初に勉強した時よく分からなかった。)そこで、Hit&Blowを通して、この式の嬉しさを理解していきます。
事前分布、尤度、事後分布
個人的にはこれらの単語の意味を抑えなくても、(動くコードが書けるので)問題ないと考えています。また、ここで文書の説明を読むよりも、具体例を見たほうが分かるようになる気がします。しかし、ベイズの本を読むと必ず出てくる単語で、かつ、よく分からないまま放置されがちな単語です。(自分も最初全く分からなかったし、今もよく分かっていない。)特に、「事前分布ってなんだよ、どう設定すればいいんよ」となりがちです。
事前分布(Prior distribution)
事前分布は、観測データを得る前の段階で、ある事象が起こると信じられる(期待される、考えられる)確率分布のことを指します。これは、過去のデータや知識、経験などに基づいて設定されます。
例えば、6面さいころに関する推定で、各目が出る確率を1/6とするとか、あるプロスポーツプレイヤーの将来の勝率に関する推定で、過去のデータから特定の相手には勝率2/3や1/3としてそれ以外は1/2とするなどです。
ここで漫画『カイジ』におけるカイジvs班長のさいころのように出る目を偏らせていたり、スポーツにおいてどの相手に対してもが本当に勝率が2/3あるようなケースに対してでも、上の事前分布の設定で問題ありません。事前分布は(十分な数のデータにより事後分布を更新するのであれば、)その確率を0にしなければ、適当に決めても問題ありません。(最終的には確率は収束することが期待できるので。証明はできないので嘘かも。)式(3)における
尤度(Likelihood)
尤度は、観測データが与えられた時、そのデータが得られる確率のことを指します。特定のパラメータ下で、観測データがどの程度"もっともらしいか"を表します。
式(3)における
事後分布(Posterior distribution)
事後分布は、観測データを考慮に入れた後の、ある事象が起こる確率分布です。これは事前分布と尤度に基づいて、ベイズの定理を用いて計算されます。
式(3)における
Hit&Blow
ここからhHit&Blowを実際に解いていくことを考えます。前節が分からなくても多分なんとかなります。
可能な数字の組み合わせ(000から999まで)
3桁のHit&Blowでは、000から999までの1000通りの組み合わせが考えられます。同じ数字を複数含む際のhit, blowの判定が(人によって異なり)面倒なため、今回は各桁の数字は相異なるとします。このとき、答えになり得る組み合わせは以下のように計算されます:
1桁目:10通り(0~9)
2桁目:9通り(1桁目以外)
3桁目:8通り(1,2桁目以外)
したがって、答えとなりえる組み合わせの総数は10 × 9 × 8 = 720通りとなります。この720通りの組み合わせそれぞれに対して、初期状態では等しく1/720の確率が割り当てられます。これはベイズ推定に際に用いる「事前分布」になります。
各ターンでの情報(Hit数とBlow数)
各ターンで得られるHitとBlowの情報は、正解の可能性がある数字の組み合わせを絞り込む重要な手がかりとなります。改めて確認すると、
- Hit:数字と桁の位置が完全に一致。強い手がかり。
- Blow:正しい数字が含まれているが位置が異なる。弱い手がかり。
となっています。
例えば、「567」が正解で「576」と推測した場合の1Hit 2Blowという情報は、以下のことを示しています:
- 1つの数字が正しい位置にある(5xx, x6x, または xx7)
- 残りの2つの数字は含まれているが、位置が異なる
このように情報を用いて、720通りから正解の数字を絞り込んでいきます。
実際にやってみる
このゲーム自体は、ベイズ推定と関係なく簡単に遊べるため、例えば以下のようなコードを書けば一人でも楽しむことができます。
#![allow(dead_code, unused_imports, unused_variables)]
use proconio::input_interactive;
use rand::Rng;
fn main() {
let ans = gen_answer();
// println!("Answer: {}", ans);
println!("Please input 3-digit number.");
let judge = Judge::new(ans);
let mut cnt = 0;
loop {
input_interactive! {
input: usize,
}
let (hit, blow) = judge.judge(input);
cnt += 1;
println!("turn {}: {} hit, {} blow", cnt, hit, blow);
if hit == 3 {
println!("Congratulation!");
break;
}
}
}
fn gen_answer() -> usize {
let mut rng = rand::thread_rng();
let mut ans = 0;
loop {
ans = rng.gen_range(0..1000);
if is_valid(ans) {
break;
}
}
ans
}
fn is_valid(n: usize) -> bool {
let digits = get_digits(n);
digits[0] != digits[1] && digits[1] != digits[2] && digits[2] != digits[0]
}
fn get_digits(mut n: usize) -> [usize; 3] {
let mut digits = [0; 3];
for i in (0..3).rev() {
digits[i] = n % 10;
n /= 10;
}
digits
}
struct Judge {
answer: [usize; 3],
}
impl Judge {
fn new(ans: usize) -> Self {
Judge { answer: get_digits(ans) }
}
fn judge(&self, input: usize) -> (usize, usize) {
let mut digits = get_digits(input);
let mut hit = 0;
let mut blow = 0;
for (i, &d) in digits.iter().enumerate() {
if self.answer[i] == d {
hit += 1;
} else if self.answer.contains(&d) {
blow += 1;
}
}
(hit, blow)
}
}
terminalで一人悲しく遊んでいる様子↓
$ ./target/release/hit_and_blow
Please input 3-digit number.
123
turn 1: 0 hit, 1 blow
456
turn 2: 0 hit, 1 blow
789
turn 3: 0 hit, 1 blow
369
turn 4: 0 hit, 1 blow
258
turn 5: 0 hit, 1 blow
126
turn 6: 0 hit, 2 blow
726
turn 7: 0 hit, 3 blow
672
turn 8: 3 hit, 0 blow
Congratulation!
...... 2回も遊べば飽きます。
本記事のこれ以降の内容につなげるために、計算機に以下のルールに従って1000回遊んでもらいます。
- 今まで宣言していない数からランダムに選んで宣言する
hitやblowのヒントを一切使わなかったとき、当たるまでに宣言した数はこのようになりました。
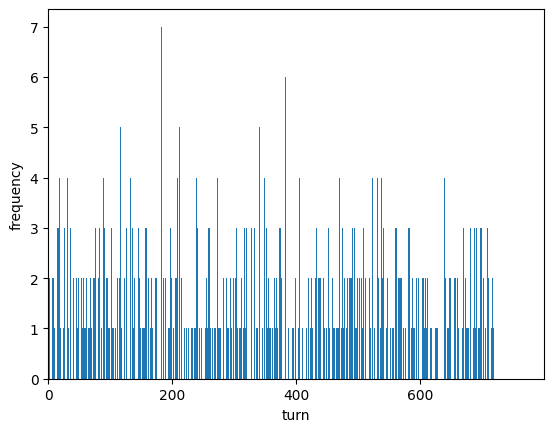
平均は349.9回で、答えの可能性が720通りであることから、約半分の回数で正解できていることが分かります。
....... いや、回数かかりすぎでしょ!!!!!
これまでの結果をもとにもっと賢く宣言すれば、正解までの回数を減らせそうな感じがします。そんなときに使うのが先ほど出てきたベイズ推定です!!
Hit&Blowへのベイズ推定の適用
ようやく本題に入ることができます。ベイズの式を改めて観測データ
Hit&Blowにおいて、観測データ
最終的に知りたいものは、
事前分布の設定
事前分布は先に述べたように割と適当でも何とかなります。今回は
尤度の計算方法(各Hit&Blow結果の確率)
続いて計算についてです。Hit&Blowでは確率が絡まない(結果について嘘をつかれることもなければ誤差が発生することもない)ので、あるデータに対してその確率は
例えば、
尤度の計算では、あるパラメータ
言葉だけだと難しいので例を考えましょう。先の例でデータ(
最初の
事後分布の更新プロセス
上のように確率を計算すると、例えば、
のように計算ができます。
""実際に計算する場面では、確率として規格化するため、分母は重要ではない場合が多い""といったのは上の計算において分母がすべて共通であるからです。候補である720通りの確率を足した和が1になればいいため、分母は計算する必要がありません。またこのような事情からベイズ推定は、
の形で書かれているのもよく目にします。
事後分布を計算すると、確率0の数字と、確率が0でない数字に分かれ、それぞれが答えとなる確率を知ることができます。今度はこの値を事前分布として、再度データを集めれば良いです。これを繰り返していくと、最終的に確率0の数字719個と確率1の数字1つになるため、Hit&Blowを解くことができます。
すみません何言っているか分からないんですが
ここまでの説明を自分も今までに何度かみて、「んんん分からん...」となっていました。もっと簡単な例を1ステップずつ追って理解を試みます。
Hit&Blowを簡単にした次のゲームを考えます。
- 2桁の数を当てる
- 各桁で使って良い数字は1,2,3の3種類のみ
- 同じ数字は一度しか使えない
- それ以外はHit&Blowと同じルール
このとき、最初の確率(事前分布、
| 11 | 12 | 13 | 21 | 22 | 23 | 31 | 32 | 33 | |
|---|---|---|---|---|---|---|---|---|---|
| 事前分布(正規化前) | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 事前分布(正規化後) | 0 | 0 | 0 |
今、答えが23だとします。そして12を宣言しました。データとして「12を宣言して"0 Hit 1 Blow"」が得られます。これをもとに尤度
| 11 | 12 | 13 | 21 | 22 | 23 | 31 | 32 | 33 | |
|---|---|---|---|---|---|---|---|---|---|
| 尤度 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
尤度と事前分布から各
| 11 | 12 | 13 | 21 | 22 | 23 | 31 | 32 | 33 | |
|---|---|---|---|---|---|---|---|---|---|
| 事前分布(正規化後) | 0 | 0 | 0 | ||||||
| 尤度 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 事後分布(正規化前) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 事後分布(正規化後) | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
今回のデータ「12を宣言して"0 Hit 1 Blow"」によって、答えは23と31がそれぞれ50%にまで絞れました。次はこれを事前分布として、再度数字を宣言し、分布を更新すればいいです。このステップを繰り返すことで、数字を推測することができます。
ポイントとしては
-
\theta_i - それぞれについてデータをもとに事後確率を計算する
- 事後確率を正規化する
ことが挙げられます。
実装
さて、先にあげたコードにベイズ推定を実装して、賢くHit&Blowを計算するように変更してみます。上のコードでmain関数からgen_answer関数までの間に新しくベイズ推定パートを実装します。考えられる全ての
Rustを使用したシミュレーションコード
#![allow(dead_code, unused_imports, unused_variables)]
use proconio::input_interactive;
use std::collections::HashSet;
use rand::Rng;
fn main() {
let mut rng = rand::thread_rng();
for _ in 0..1 {
let ans = gen_answer();
println!("Answer: {}", ans);
println!("Please input 3-digit number.");
let judge = Judge::new(ans);
let mut hs = HashSet::new();
//事前分布の初期化
let mut probs: Vec<f64> = vec![0.0; 1000];
for i in 0..1000 {
if is_valid(i) {
probs[i] = 1.0;
}
}
//正規化
normalize(&mut probs);
//ベイズ推定を用いた探索
let mut cnt = 0;
loop {
//現時点で最も確率が高い数字をinputとして選択
let mut input = 0;
let mut max_prob = 0.0;
for i in 0..1000 {
if probs[i] > max_prob && !hs.contains(&i) {
input = i;
max_prob = probs[i];
}
}
println!("input: {}, prob: {}", input, max_prob);
hs.insert(input);
let (hit, blow) = judge.judge(input);
cnt += 1;
println!("turn {}: {} hit, {} blow", cnt, hit, blow);
if hit == 3 {
println!("Congratulation!");
break;
}
//ベイズ推定
bayes_update(&mut probs, input, (hit, blow));
}
println!("{}", cnt);
}
}
fn normalize(probs: &mut Vec<f64>) {
let sum = probs.iter().sum::<f64>();
probs.iter_mut().for_each(|x| *x /= sum);
}
fn bayes_update(probs: &mut Vec<f64>, input: usize, (hit, blow): (usize, usize)) {
//尤度の計算
let mut likelihoods = vec![0.0; 1000];
let mut judge = Judge::new(input);
for i in 0..1000 {
if is_valid(i) {
let (h, b) = judge.judge(i);
if h == hit && b == blow {
likelihoods[i] = 1.0;
}
}
}
//事後確率の更新
probs.iter_mut().zip(likelihoods.iter()).for_each(|(x, y)| *x *= y);
normalize(probs);
}
//gen_answer以降省略
結果
人の手は介入しないため、あらかじめ答えを表示させ、どのような数字をどの程度の確率で宣言しているのかを見てみます。1回試してみると次のような感じです。
Answer: 960
Please input 3-digit number.
input: 12, prob: 0.001388888888888889
turn 1: 0 hit, 1 blow
input: 134, prob: 0.003968253968253979
turn 2: 0 hit, 0 blow
input: 256, prob: 0.012500000000000011
turn 3: 0 hit, 1 blow
input: 507, prob: 0.041666666666666664
turn 4: 0 hit, 1 blow
input: 680, prob: 0.16666666666666669
turn 5: 1 hit, 1 blow
input: 960, prob: 1
turn 6: 3 hit, 0 blow
Congratulation!
何が起こっているのかこの結果からはあまりよく分かりませんが、かなり少ない回数で推測できていそうです。123~987の答えとして考えられる720通り全てについて一回ずつ試して、答えを当てるまでにかかった数字を見てみます。
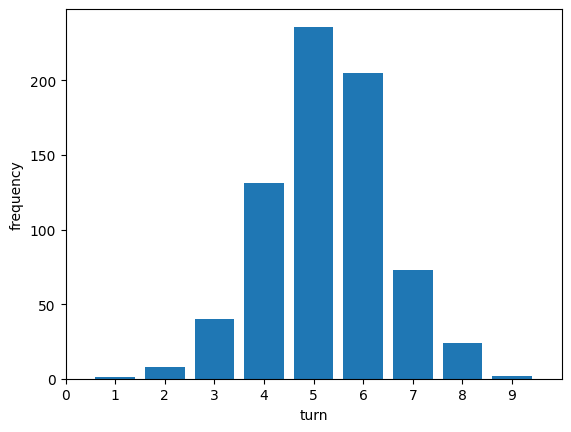
平均は5.27回と、先のランダムな方法から大幅に改善しました!!
発展的話題
より効率的なアルゴリズムの検討
平均5.27回と少ない回数で数字を推測することができました。しかし少し考えると、まだこのコードは改善の余地があることが分かります。
今、数字を宣言する際に、答えとなる確率が最も高い数字を宣言していました。例えば先の例だと、最初に
このように既に分かっている情報をもとに行動することを「活用(exploitation)]といい、逆に
(Hit&Blowの亜種で、"1 Hit 1 Blow"等の代わりに、答えと宣言した数の差に、さらに適当な誤差をいれて返してくれる問題とかも考えてみたい。答えが345で123と宣言した時に、200(差が223で23の誤差付き)が返ってくるような問題。誤差を正規分布とかにすれば、ベイズ推定で問題なく扱うことができるはず。)
まとめ
本記事では、Hit&Blowという身近(?)なゲームを通じて、ベイズ推定のの理解を深めました。
まず、ベイズ推定の基本概念である事前分布、尤度、事後分布について、具体的な例を用いて説明し、理論と実践のつながりを示しました。これにより、抽象的な概念を直感的に理解できるようになっていれば幸いです。
次に、Rustを使用して実際のシミュレーションコードを提示し、理論を実装に落とし込みました。これにより、自分で実装する際の参考にしてもらえれば幸いです。
さらに、ランダムな方法とベイズ推定を用いた方法の結果を比較し、ベイズ推定の効果を定量的に示しました。平均試行回数が349.9回から5.27回に大幅に改善されたことは、このアプローチの有効性を明確に示しています。
次回の記事では、この問題に対するアプローチとして「相互情報量」の概念を導入し、より短い手数で数字を当てることを目指します。これにより、ベイズ推定の応用をさらに深く探求し、より効率的なアルゴリズムの開発に取り組みます。
本記事がベイズ推定の理解を深め、実践的なスキルを身につける一助となれば幸いです。
Discussion