I はイデアルである.
ということで,今回からイデアル格子暗号についての解説記事を連載していきます.対象とするペーパーは
イデアル格子暗号入門
こちらになります.ドキュメントというか論文っぽくはないですが,以下では論文と呼ぶことにします.
本論文は,準同型暗号を用いた秘密計算の資料として大体紹介されるものですが,実際のところ中身はどうなんだというところに注目します.
実は何回かすでに読んでいるのですが,数学的な「整備」が必要な部分もいくつかあってモヤっていたので,今回ではっきりできたらなと思っています.
連載記事の雰囲気は
プログラマブルブートストラップの原著論文を理解する回 1/4
プログラマブルブートストラップの原著論文を理解する回 2/4
プログラマブルブートストラップの原著論文を理解する回 2.5/4
プログラマブルブートストラップの原著論文を理解する回 3/4
プログラマブルブートストラップの原著論文を理解する回 4/4
これと同じようなものを目指します.
理論の解説はもちろん,周辺の数学的な議論など大雑把な部分をはっきりさせることを目標にします.説明の都合上,論文に記載の記号とはずれることがある(早速ずれる)のですが,こっちの方が意味が伝わりやすいかなと思って修正していますので何卒.
突貫で書いてしまった部分もあるので,大いに誤りを含む可能性があります.誤字・脱字レベルでも構いませんので,ご指摘ください.
また,予告なしに内容の加筆や構成の変更を行うことがありますが,読みやすくするためのものですので,ご容赦ください
全3回通しでの目次
第1回
- 本論文全体の流れ
- 前提知識
- 今回出てくる予備知識のまとめ
- 1の3乗根
- 3分整数
- p分整数
- m分整数
- イデアル
- 衝突困難関数とSVP
第1.5回
- 記号の整理
- 衝突困難関数の構成
- 衝突困難関数の簡単な例
- 構成の証明の方針
- 構成の正当性の証明
第2回
第3回
今回は第1回です.具体的な内容としては,次のようになります:
- 本論文全体の流れ
- 前提知識
- 今回出てくる予備知識のまとめ
- 1の3乗根
- 3分整数
- p分整数
- m分整数
- イデアル
- 衝突困難関数とSVP
本論文全体の流れ
- どういう背景や課題・モチベーションがあって,
- どのようなアイディアのもとで,
- どのような結果が得られたのか
を整理します.
背景・課題
RSA暗号は量子計算機で破られることから,別のアプローチからの暗号方式が必要です
その1つが格子暗号であり,更に何かしらの「機能」を加えたいというモチベーションがあります
アイディア
通常の整数を拡張した円分整数上での暗号方式(公開鍵)を考え,更にその方式は準同型性を満たしています
結果
準同型性のうち,掛け算は非自明な構成ですが,足し算・掛け算共にうまくいく暗号方式を構成でき増した
それらを元に各章を整理すると,次のようになります:
1章:イントロ
2章:前提知識
3章:衝突困難関数の構成
4章:準同型暗号の構成
5章:まとめ
つまり,3章と4章が一番言いたいことになります.
ただ,3章は,4章以降の議論には関係ないので,ここはさらっと扱う程度にして,4章をメインに扱います.
前提知識
以下↓は,プログラマブルブートストラップの原著論文を理解する回 1/4「今回出てくる予備知識のまとめ」 のコピペです
なるべく丁寧に解説することは心がけますが,
- (素朴)集合論(\neq 公理的集合論):全射・単射・全単射・直積
- 線型代数:行列の和や積・行列式
- 確率・統計:確率分布・確率密度関数
- 代数:Abel群・可換環・体の定義
- 初等整数論:mod
- 計算量理論:クラスPとNP
ぐらいは前提知識とします(サイレント修正の可能性あり).知らなくてもググればどうにかなるかもです.
他に必要なものは,論文解説で使用するものは本文中,補足で必要なものは折りたたみで必要になったときに定義します.
また,次の記号を使います(使わないものもあるかもですが):
-
\mathbb{N} : 自然数全体の集合,0を含む
-
\mathbb{Z} : 整数全体の集合
-
\mathbb{Q} : 有理数全体の集合
-
\mathbb{R} : 実数全体の集合
-
\mathbb{C} : 複素数全体の集合
- \mathbb{B} = \{0, 1 \}
-
x \overset{\#}{\leftarrow} X : 集合 X から要素 x をランダムに取る
- Def : 定義
- Thm : 定理
*ランダムに取るときの記号は本当は$で出力したいのですが,なんか数式モードだと上手くいかない?ようなので#で代用します(有識者教えてください)
主に参考にする書籍を以下で挙げます(最後に載せているのと同じ).ただ割と数学色が強いので,
線形代数と確率・統計は自分でやる
→代数と計算量理論は暗号の本を見る
が手っ取り早いのかなって思っています(あまりよく知らない).
↓ステマではないです
集合論
初学者向け
集合と位相空間
かなりまとまっている本
集合と位相(増補新装版)(数学シリーズ)
線型代数
初学者向け
線型代数
数学書っぽい雰囲気を味わいたい方向け,あとは加群を見据えて単因子論をやりたい方向け
線型代数入門
確率・統計
実用性のコスパ的には一番良い気がします
統計学入門
代数
群の初学者向け(たぶん)
代数学1 群論入門
環・環上の加群・Galois理論の初学者向け(環以外は少し読みづらいかも)
代数学2 環と体とガロア理論
群・環・環上の加群を復習したい方むけ(初学はかなりきつそう)
代数入門(新装版): 群と加群 (数学シリーズ)
環上の加群(あまり読んでないです)
代数学〈2〉環上の加群 (大学数学の入門)
体・Galois理論の初学者向け(薄いけど例もきっちり書かれています)
代数学〈3〉体とガロア理論 (大学数学の入門)
*環上の加群,は「ホモロジー代数」を扱った本でも良いと思います(僕はそれで読んだ)
初等整数論
上の代数学シリーズの数論版(代数もまとまっているのでこれだけで良い感はある())
整数論1: 初等整数論からp進数へ
個人的にはこっちの方が好きです(僕の大学の先生方も関わっています)
初等整数論 ―数論幾何への誘い― (共立講座 数学探検 6)
計算量理論
計算理論の基礎 [原著第2版] 2.計算可能性の理論
代数とか計算量理論が載っている暗号の本
マジの聖書(耐量子計算機暗号に多かれ少なかれ関わっている方はもちろん,数学的に量子計算や高機能暗号を捉えたい方に勧められます.量子計算機の共通鍵暗号への影響もちらっとだけ触れられていて,本当に痒いところに手が届く本です)
(ですが,計算量や代数は載っているもののかなりさらっと書かれているので,初学向けではないです)
耐量子計算機暗号
代数だけならつい最近にいい感じの本が出ましたね
暗号から学ぶ代数学 (数学のみかた,考え方)
以下は洋書ですが良い本が多いです
1冊目は「正統派」な本で,
2冊目は「代数」・3冊目は「計算量・ロジック」・4冊目は「アルゴリズムなどの手法」から暗号を眺める本です.
5冊目・6冊目は僕が勉強するときに使っていた(今でも読んでいる)本です
1冊目
暗号の授業をしろ,と言われたらこれを参照するかなと(古典的な内容は網羅されています)
Understanding Cryptography: A Textbook for Students and Practitioners
2冊目
ここの要望に応えてくれる本
代数・初等整数論も計算量も書かれていて,格子も割と充実しています,英語に抵抗のない暗号理論の初学者に1冊薦めるならこれです
An Introduction to Mathematical Cryptography (Undergraduate Texts in Mathematics)
3冊目
ロジックの視点から始まり,NL完全とかPPなど計算量の観点から眺める本(代わりに代数はあっさり)
Complexity Theory and Cryptology
4冊目
アルゴリズム以外も色々書いてあります,体の拡大とか必要なんか?(計算量の記述が少ないのが惜しい)
Cryptography Made Simple (Information Security and Cryptography)
5冊目
「one-way」・「psueudorandom」・「zero-knowledge」がかなり丁寧に書かれていて,これらを読むだけでも相当な実力になるかと(お陰でくどいし長い)
Foundations of Cryptography v1
6冊目
5冊目の続き,徹底的にセキュリティを定式化するって感じです(上もそうですが,厳密に暗号を扱いたい方向けかなと)
Foundations of Cryptography
今回出てくる予備知識のまとめ
前提知識以外の数学的な予備知識は適宜まとめてはいますが,一覧がほしい方もいらっしゃるかもなので,先にまとめます.折りたたみで出てくる概念のみを対象で,本文中に出てくるものは目次を参考にしてください.
順番は今回の記事で出てくる順で,内容は定義だけざっと並べています.
- 巡回群
- 線型独立
- 基底
- 原始n乗根
- 円分多項式
- イデアル
巡回群
\underline{\mathrm{Def(巡回群)}}
G を群,S を G の部分集合とする.x_1, x_2, \cdots, x_n \in S により,x_1^{\pm 1} x_2^{\pm 1} \cdots x_n^{\pm 1} の形をした G の元を S の元による語という.
\langle S \rangle を S の元による語全体の集合として,S によって,生成された部分群という.
S の元が1つのとき,\langle S \rangle を巡回群という.
線型独立
\underline{\mathrm{Def(線型結合)}}
体 K 上の n 次元ベクトル空間 V において,V のベクトル a_1, a_2, \cdots, a_k に対して,c_1 a_1 + c_2 a_2 + \cdots + c_k a_k \ (c_i \in K) なるベクトルを a_1, a_2, \cdots, a_k の線型結合という.
\underline{\mathrm{Def(線型関係)}}
体 K 上の n 次元ベクトル空間 V において,V のベクトル a_1, a_2, \cdots, a_k に対して,c_1 a_1 + c_2 a_2 + \cdots + c_k a_k = 0 \ (c_i \in K) なる関係を線型関係という.
c_1 = c_2 = \cdots = c_k = 0 なる関係を自明な線型関係という.
\underline{\mathrm{Def(線型従属・独立)}}
体 K 上の n 次元ベクトル空間 V において,V のベクトル a_1, a_2, \cdots, a_k に対して,自明でない線型関係が存在するとき,a_1, a_2, \cdots, a_k は線型従属であるといい,自明でない線型関係が存在しないとき,a_1, a_2, \cdots, a_k は線型独立であるという.
基底
\underline{\mathrm{Def(基底)}}
体 K 上の n 次元ベクトル空間 V において,n 個の V のベクトル a_1, a_2, \cdots, a_n が次の2つの条件を満たすとき,a_1, a_2, \cdots, a_n は V の基底であるという.
(i) a_1, a_2, \cdots, a_n は線型独立
(ii) V の任意のベクトルは,a_1, a_2, \cdots, a_n の線型結合で表せる
原始n乗根
\underline{\mathrm{Def(n乗根と原始n乗根, nth \ root \ and \ primitve \ nth \ root)}}
n を正整数とするとき,z \in \mathbb{C} であって,z^n = 1 を満たす z を1の n 乗根という.
\zeta が1の n 乗根であり,0 < m < n で \zeta^m \neq 1 を満たすとき,\zeta を1の原始 n 乗根という.
円分多項式
\underline{\mathrm{Def(円分多項式, cyclotomic \ polynomial)}}
n を正整数,\zeta_n \in \mathbb{C} を1の原始 n 乗根とするとき,n 次の円分多項式 \Phi_n(X) は次のように表せる:
\begin{align*} \displaystyle
\Phi_n(X) = \prod_{1 \leq i \leq n, iとnは互いに素} (X - \zeta_n^i)
\end{align*}
イデアル
\underline{\mathrm{Def(イデアル)}}
m 分整数 g = g_0 + g_1 \zeta_n + \cdots + g_{n - 1} \zeta_n^{n - 1} に対して,次の集合 I_g をイデアルという:
\begin{align*}
I_g = \{ a_0 g + a_1 \zeta_n g + \cdots + a_{n - 1} \zeta_n^{n - 1} g \ | \ a_0, a_1, \cdots, a_{n - 1} \in \mathbb{Z} \}
\end{align*}
1の3乗根
突然ですが,\displaystyle \zeta_3 = \frac{-1 + \sqrt{-3}}{2} を考えます.\sqrt{-3} = \sqrt{-1 \cdot 3} = \sqrt{3} \cdot \sqrt{-1} ですので,\sqrt{-1} は実数ではありませんから,\zeta_3 も実数ではありません.
視点を変えてみると,\displaystyle \zeta_3 = \frac{-1}{2} + \frac{\sqrt{-3}}{2} = \frac{-1}{2} + \frac{\sqrt{3} \cdot \sqrt{-1}}{2} = \frac{-1}{2} + \frac{\sqrt{3}}{2} \sqrt{-1} と考えることができます.さて,唐突ですが,\displaystyle \cos \left( \frac{2 \pi}{3} \right) = \frac{-1}{2}, \ \sin \left( \frac{2 \pi}{3} \right) = \frac{\sqrt{3}}{2} なので,\displaystyle \zeta_3 = \cos \left( \frac{2 \pi}{3} \right) + \sin \left( \frac{2 \pi}{3} \right) \sqrt{-1} となります.
つまり,\zeta_3 を図示すると次のようになります:

ここで,\zeta_3^2 を計算してみましょう.
\begin{align*}
\displaystyle
\zeta_3^2
& = \left( \frac{-1}{2} + \frac{\sqrt{3}}{2} \sqrt{-1} \right)\left( \frac{-1}{2} + \frac{\sqrt{3}}{2} \sqrt{-1} \right) \\
& = \left( \frac{1}{4} + \frac{3}{4} (-1) \right) + \left( 2 \cdot \frac{-1}{2} \frac{\sqrt{-3}}{2} \right) \sqrt{-1} \\
& = \frac{- 1}{2} + \frac{- \sqrt{3}}{2} \sqrt{-1} \\
& = \cos \left( \frac{4 \pi}{3} \right) + \sin \left( \frac{4 \pi}{3} \right) \sqrt{-1} \\
& = \cos \left( \frac{2 \cdot 2 \pi}{3} \right) + \sin \left( \frac{2 \cdot 2 \pi}{3} \right) \sqrt{-1}
\end{align*}
このようになります.こちらも図示すると次のようになります:

ここで,\zeta_3 と \zeta_3^2 を見比べると,\zeta_3^2 は \zeta_3 の角度を2倍にしたものに対応しています.すると,\zeta_3^3 は \zeta_3 の角度を3倍にしたものに対応しそうです.
*De Moivreの定理 と呼ばれるものです
このことから,\displaystyle \cos \left( \frac{3 \cdot 2 \pi}{3} \right) + \sin \left( \frac{3 \cdot 2 \pi}{3} \right) \sqrt{-1} = \cos (2 \pi) + \sin (2 \pi) \sqrt{-1} = 1 を得られます.実際,
\begin{align*}
\displaystyle
\zeta_3^3 = \zeta_3 \cdot \zeta_3^2
& = \left( \frac{-1}{2} + \frac{\sqrt{3}}{2} \sqrt{-1} \right) \left( \frac{- 1}{2} + \frac{- \sqrt{3}}{2} \sqrt{-1} \right) \\
& = \left( \frac{1}{4} + \frac{-3}{4} (-1) \right) + \left( \frac{3}{4} + \frac{-3}{4} \right) \sqrt{-1} \\
& = 1 + 0 \cdot \sqrt{-1} \\
& = 1
\end{align*}
となります.つまり,\zeta_3 は3乗すると1になる,ということは\zeta_3 は X^3 - 1 = 0 の解(\zeta_3 は X^3 - 1 の根)になります.X^3 - 1 = 0 の解を考えると,X = 1 は自明で,X = \zeta_3 も解になることが分かりました.
X^3 - 1 = 0 の解は3つあるので,1, \zeta_3 以外にもう1つあります.それは \zeta_3^2 です.
上記を確かめる
\zeta_3^2 が X^3 - 1 = 0 の解になっているかどうかは,(\zeta_3^2)^3 = 1 かどうかを確かめればOKです.
\begin{align*}
\displaystyle
(\zeta_3^2)^2
& = \left( \frac{- 1}{2} + \frac{- \sqrt{3}}{2} \sqrt{-1} \right) \left( \frac{- 1}{2} + \frac{- \sqrt{3}}{2} \sqrt{-1} \right) \\
& = \left( \frac{1}{4} + \frac{3}{4} (-1) \right) + 2 \left( \frac{-1}{2} \right) \left( \frac{- \sqrt{3}}{2} \right) \sqrt{-1} \\
& = \frac{-1}{2} + \frac{\sqrt{3}}{2} \sqrt{-1}
\end{align*}
\begin{align*}
\displaystyle
(\zeta_3^2)^3 = (\zeta_3^2) (\zeta_3^2)^2
& = \left( \frac{- 1}{2} + \frac{- \sqrt{3}}{2} \sqrt{-1} \right) \left( \frac{-1}{2} + \frac{\sqrt{3}}{2} \sqrt{-1} \right) \\
& = \left( \frac{1}{4} + \frac{- 3}{4} (-1) \right) + \left( \frac{- \sqrt{3} + \sqrt{3}}{4} \right) \sqrt{-1} \\
& = 1 + 0 \sqrt{-1} \\
& = 1
\end{align*}
よって,示されました.
つまり,X^3 - 1 = 0 の解は X = \zeta_3, \zeta_3^2, 1 の3つです.これらを極座標表示すると,
\begin{align*}
\displaystyle
X = \cos \left( \frac{2 \pi}{3} \right) + \sin \left( \frac{2 \pi}{3} \right) \sqrt{-1}, \cos \left( \frac{2 \cdot 2 \pi}{3} \right) + \sin \left( \frac{2 \cdot 2 \pi}{3} \right) \sqrt{-1}, \cos \left( \frac{3 \cdot 2 \pi}{3} \right) + \sin \left( \frac{3 \cdot 2 \pi}{3} \right) \sqrt{-1}
\end{align*}
となっています.これらを図示すると,次のようになります.

つまり,X^3 - 1 = 0 の解は,単位円周上にちょうど3等分する位置に存在しています.
さらに,k を自然数とすると,\zeta_3^{3 k} = 1 であることが分かります.\zeta_3^{3k} = (\zeta_3^3)^{k} = 1^k = 1 となるからです.とすると,\zeta_3^{3k + 1} = \zeta_3^{3k} \zeta_3 = \zeta_3 ですし,\zeta_3^{3k + 2} = \zeta_3^{3k} \zeta_3^2 = \zeta_3^2 です.
そして,もう1つ,\zeta_3 と \zeta_3^2 の関係について,今一度考察しましょう.それぞれの値は,
\begin{align*}
\displaystyle
\zeta_3 & = \frac{-1}{2} + \frac{\sqrt{3}}{2} \sqrt{-1} \\
\zeta_3^2 & = \frac{-1}{2} - \frac{\sqrt{3}}{2} \sqrt{-1}
\end{align*}
でした.実は,ここでグッと睨むと,\zeta_3^2 = - 1 - \zeta_3 であることが分かります.実際,
\begin{align*}
\displaystyle
- 1 - \zeta_3 & = - 1 - \left( \frac{-1}{2} + \frac{\sqrt{3}}{2} \right) = \frac{-1}{2} - \frac{\sqrt{3}}{2}
\end{align*}
ですので,確かに \zeta_3^2 = - 1 - \zeta_3 が成り立ちます.
(この性質は,閃きによるものなのか・・・!と思った方もいらっしゃるかもしれませんが,実は案外簡単なものです)
種明かし
重要な部分は,
つまり,X^3 - 1 = 0 の解は,単位円周上にちょうど3等分する位置に存在しています.
です(後でもう一度引用します).
ここで,X^3 - 1 = (X - 1)(X^2 + X + 1) ですから,X^3 - 1 = 0 というのは,(X - 1)(X^2 + X + 1) = 0,つまり,X - 1 = 0 または X^2 + X + 1 = 0 ということになります.X - 1 = 0 の方から X = 1 が分かります.
X^2 + X + 1 = 0 については,2次方程式の解の公式を使うと,\zeta_3, \zeta_3^2 が解になることが分かります.逆に X = \zeta_3 は X^2 + X + 1 = 0 の解なので,\zeta_3^2 + \zeta_3 + 1 = 0 となります.よって,\zeta_3^2 = - 1 - \zeta_3 を得られました.
これの何が凄いかっていうと,\zeta_3^2 の値を知りたいときに,わざわざ \zeta_3 \cdot \zeta_3 をする必要はない,ということです.
これらの事実を一旦まとめておきましょう.
\underline{\mathrm{Def(1の3乗根)}}
X^3 - 1 = 0 の解のうち,X = 1 以外のものを X = \zeta_3 と置くと,もう1つの解は \zeta_3^2 と表せる.\zeta_3 のことを1の3乗根という.
\underline{\mathrm{Prop(1の3乗根)}}
1の3乗根 \zeta_3 について,k を自然数とすると,次が成り立つ:
\begin{align*}
\zeta_3^2 & = -1 - \zeta_3 \\
\zeta_3^{3k} & = 1 \\
\zeta_3^{3k + 1} & = \zeta_3 \\
\zeta_3^{3k + 2} & = \zeta_3^2 \\
\end{align*}
*群論に少し慣れている方向けだと,\zeta_3 で生成される群が巡回群,と書いた方が分かりやすいかもです
巡回群
\underline{\mathrm{Def(巡回群)}}
G を群,S を G の部分集合とする.x_1, x_2, \cdots, x_n \in S により,x_1^{\pm 1} x_2^{\pm 1} \cdots x_n^{\pm 1} の形をした G の元を S の元による語という.
\langle S \rangle を S の元による語全体の集合として,S によって,生成された部分群という.
S の元が1つのとき,\langle S \rangle を巡回群という.
例えば,群 \mathbb{Z} について,2で生成される群 2 \mathbb{Z} は巡回群です.
上の定義からも分かりますが,実は \zeta_3^2 の方を \zeta_3 とみなしても本質的な議論は変わりません(が,偏角が大きい方を採用する必要もないので,一般には \displaystyle \frac{2 \pi}{3} の方を \zeta_3 とします).
また,\zeta_3 は,1の原始3乗根などと呼ばれることもありますが,それは 今回の「m分整数」 で解説します.
3分整数
ここまで,色々と \zeta_3 について調べてきました.これからは,\zeta_3 そのものではなく,\zeta_3 を使って表せる「数」について考察します.
\underline{\mathrm{Def(3分整数)}}
a_0, a_1 を整数とするとき,a_0 + a_1 \zeta_3 の形の整数を3分整数という.
3分整数全体の集合 \{ a_0 + a_1 \zeta_3 \ | \ a_0, a_1 \in \mathbb{Z} \} を \mathbb{Z}[\zeta_3] と書く.
a_0 + a_1 \zeta_3 というのは,正確には a_0 \cdot 1 + a_1 \zeta_3 です.すると,1つ疑問に思った方もいらっしゃるかもしれません.3分整数って a_0 + a_1 \zeta_3 ではなく,a_0 + a_1 \zeta_3 + a_2 \zeta_3^2 じゃないの?というものです.
結論から書くと,a_0 + a_1 \zeta_3 で合っています.\zeta_3^2 が1と \zeta_3 の足し算とスカラー倍で表される(線型結合)ためです.
線型独立
\underline{\mathrm{Def(線型結合)}}
体 K 上の n 次元ベクトル空間 V において,V のベクトル a_1, a_2, \cdots, a_k に対して,c_1 a_1 + c_2 a_2 + \cdots + c_k a_k \ (c_i \in K) なるベクトルを a_1, a_2, \cdots, a_k の線型結合という.
\underline{\mathrm{Def(線型関係)}}
体 K 上の n 次元ベクトル空間 V において,V のベクトル a_1, a_2, \cdots, a_k に対して,c_1 a_1 + c_2 a_2 + \cdots + c_k a_k = 0 \ (c_i \in K) なる関係を線型関係という.
c_1 = c_2 = \cdots = c_k = 0 なる関係を自明な線型関係という.
\underline{\mathrm{Def(線型従属・独立)}}
体 K 上の n 次元ベクトル空間 V において,V のベクトル a_1, a_2, \cdots, a_k に対して,自明でない線型関係が存在するとき,a_1, a_2, \cdots, a_k は線型従属であるといい,自明でない線型関係が存在しないとき,a_1, a_2, \cdots, a_k は線型独立であるという.
線型従属(独立)であるかどうかの判定は,線型関係からだと難しそうに見えますが,a_1, a_2, \cdots, a_k を並べた行列がフルランクかどうか(フルランクなら線型独立で,そうでないなら線型従属)で判定できます.
基底
\underline{\mathrm{Def(基底)}}
体 K 上の n 次元ベクトル空間 V において,n 個の V のベクトル a_1, a_2, \cdots, a_n が次の2つの条件を満たすとき,a_1, a_2, \cdots, a_n は V の基底であるという.
(i) a_1, a_2, \cdots, a_n は線型独立
(ii) V の任意のベクトルは,a_1, a_2, \cdots, a_n の線型結合で表せる
上記の証明
\displaystyle \zeta_3 = \frac{-1}{2} + \frac{\sqrt{3}}{2} \sqrt{-1}, \ \zeta_3^2 = \frac{-1}{2} - \frac{\sqrt{3}}{2} \sqrt{-1} なので,
\begin{align*}
\displaystyle
a_0 + a_1 \zeta_3 + a_2 \zeta_3^2
& = a_0 + a_1 \left( \frac{-1}{2} + \frac{\sqrt{3}}{2} \sqrt{-1} \right) + a_2 \left( \frac{-1}{2} - \frac{\sqrt{3}}{2} \sqrt{-1} \right) \\
& = \left( a_0 + a_1 \frac{-1}{2} + a_2 \frac{-1}{2} \right) + \left( a_1 \frac{\sqrt{3}}{2} + a_2 (- \frac{\sqrt{3}}{2}) \right) \sqrt{-1}
\end{align*}
となります.よって,
\begin{align*}
\displaystyle
a_0 + a_1 \zeta_3 + a_2 \zeta_3^2
& = \left( a_0 + a_1 \frac{-1}{2} + a_2 \frac{-1}{2} \right) + \left( a_1 \frac{\sqrt{3}}{2} + a_2 (- \frac{\sqrt{3}}{2}) \right) \sqrt{-1} \\
& = \left( (a_0 - a_2) + (a_1 - a_2) \frac{-1}{2} \right) + (a_1 - a_2) \left( \frac{\sqrt{3}}{2} \right) \sqrt{-1} \\
& = (a_0 - a_2) + (a_1 - a_2) \left( \frac{-1}{2} + \frac{\sqrt{3}}{2} \sqrt{-1} \right) \\
& = (a_0 - a_2) + (a_1 - a_2) \zeta_3
\end{align*}
を得られます.つまり,a_0 + a_1 \zeta_3 + a_2 \zeta_3^2 を表現したいなら,(a_0 - a_2) + (a_1 - a_2) \zeta_3 で表せる,ということになります.
基底と結びつける
これはどういうことかというと,a_0 + a_1 \zeta_3 + a_2 \zeta_3^2 = 0 という線型関係は自明でない関係を持つ,つまり,1, \zeta_3, \zeta_3^2 は線型従属であることになります.
実際,a_0 + a_1 \zeta_3 + a_2 \zeta_3^2 = 0 のとき,(a_0 - a_2) + (a_1 - a_2) \zeta_3 + 0 \zeta_3^2 = 0 と変形できます.
また,行列表示で考えると,
\begin{align*}
\displaystyle
1 &= \begin{pmatrix}
1 & 0
\end{pmatrix}
\begin{pmatrix}
1 \\ \sqrt{-1}
\end{pmatrix} \\
\zeta_3 &= \begin{pmatrix}
\frac{-1}{2} & \frac{\sqrt{3}}{2}
\end{pmatrix}
\begin{pmatrix}
1 \\ \sqrt{-1}
\end{pmatrix} \\
\zeta_3^2 &= \begin{pmatrix}
\frac{-1}{2} & \frac{- \sqrt{3}}{2}
\end{pmatrix}
\begin{pmatrix}
1 \\ \sqrt{-1}
\end{pmatrix}
\end{align*}
なので,係数部分だけを並べた行列としては,
\displaystyle
\begin{align*}
\begin{pmatrix}
1 & 0 \\
\frac{-1}{2} & \frac{\sqrt{3}}{2} \\
\frac{-1}{2} & \frac{- \sqrt{3}}{2}
\end{pmatrix}
\end{align*}
ですので,行基本変形を行うと,
\displaystyle
\begin{align*}
\begin{pmatrix}
1 & 0 \\
0 & \frac{\sqrt{3}}{2} \\
0 & 0
\end{pmatrix}
\end{align*}
となり,上記の行列はフルランクではないため,a_0 + a_1 \zeta_3 + a_2 \zeta_3^2 = 0 について,線型従属であると分かります.
以下では,\mathbb{Z}[\zeta_3] にどのような代数構造が入るかに注目します.一般には環の構造が入ります.
\underline{\mathrm{Def(3分整数環)}}
\mathbb{Z}[\zeta_3] について,次の演算を定める(a_0, a_1, b_0, b_1 \in \mathbb{Z}):
\begin{align*}
(a_0 + a_1 \zeta_3) + (b_0 + b_1 \zeta_3) & = (a_0 + b_0) + (a_1 + b_1) \zeta_3 \\
(a_0 + a_1 \zeta_3) \cdot (b_0 + b_1 \zeta_3) & = (a_0 b_0 - a_1 b_1) + (a_0 b_1 + a_1 b_0 - a_1 b_1) \zeta_3
\end{align*}
上記の演算は共に閉じており,更に,\mathbb{Z}[\zeta_3] はこれらの演算で環になる.
*少し代数に詳しい方なら,\mathbb{Z}[\zeta_3] は \mathbb{Z}[X] / (X^3 - 1) に同型,と書いた方が伝わりやすいかもしれません
まず,これらの演算が本当に閉じているのかを確認しようと思います.
それは,a_0, a_1, b_0, b_1 \in \mathbb{Z} のとき,a_0 + b_0, a_1 + b_1, a_0 b_0 - a_1 b_1, a_0 b_1 + a_1 b_0 - a_1 b_1 \in \mathbb{Z} かどうか確かめればよいです.\mathbb{Z} は環(整数環)なので,特に「通常の」足し算と掛け算で閉じています.よって,a_0 + b_0, a_1 + b_1, a_0 b_0 - a_1 b_1, a_0 b_1 + a_1 b_0 - a_1 b_1 \in \mathbb{Z} が成り立つので,\mathbb{Z}[\zeta_3] は上記の足し算と掛け算で閉じていることが分かりました.
掛け算を深掘りする
足し算は分かりやすいですね.各係数を足しただけです.
掛け算はというと,各係数を掛けたものではありません.訳の分からない定義のように見えますが,一体どういうことなのかと思って,展開してみましょう.
(a_0 + a_1 \zeta_3) \cdot (b_0 + b_1 \zeta_3) = (a_0 b_0) + (a_0 b_1 + a_1 b_0) \zeta_3 + a_1 b_1 \zeta_3^2 となります.しかし,ここで1つ問題が起こります.\mathbb{Z}[\zeta_3] はあくまで,a_0 + a_1 \zeta_3 という形で表される元の集合なのですが,\zeta_3^2 が含まれてしまいます.
ここで役立つのが 今回の「1の3乗根」 のPropです.\zeta_3^2 = - 1 - \zeta_3 でした.これを使うと,
\begin{align*}
(a_0 + a_1 \zeta_3) \cdot (b_0 + b_1 \zeta_3)
&= (a_0 b_0) + (a_0 b_1 + a_1 b_0) \zeta_3 + a_1 b_1 \zeta_3^2 \\
&= (a_0 b_0) + (a_0 b_1 + a_1 b_0) \zeta_3 + a_1 b_1 (- 1 - \zeta_3) \\
&= (a_0 b_0 - a_1 b_1) + (a_0 b_1 + a_1 b_0 - a_1 b_1) \zeta_3
\end{align*}
となります.
つまり,定義されている掛け算は,「通常の多項式としての掛け算に \zeta_3^2 = - 1 - \zeta_3 の制約を加えたもの」と見ることができます.
何も突飛な定義ではなく,いたって自然な定義であることが分かりましたね.
さて,上記の定義では,論文よりも強く「環」と定義しました.種々の性質が成り立つか確認してみましょう.
環であることの証明
足し算と掛け算で閉じていることは確認済みなので,それぞれについて調べます.以下,a_0, a_1, b_0, b_1, c_0, c_1 \in \mathbb{Z} とします.
加法
結合律
\begin{align*}
((a_0 + a_1 \zeta_3) + (b_0 + b_1 \zeta_3)) + (c_0 + c_1 \zeta_3)
&= ((a_0 + b_0) + (a_1 + b_1) \zeta_3) + (c_0 + c_1 \zeta_3) \\
&= (a_0 + b_0 + c_0) + (a_1 + b_1 + c_1) \zeta_3 \\
&= (a_0 + a_1 \zeta_3) + ((b_0 + c_0) + (b_1 + c_1) \zeta_3)
\end{align*}
単位元
0 + 0 \cdot \zeta_3 が単位元です
逆元
a_0 + a_1 \zeta_3 に対して,(- a_0) + (- a_1) \zeta_3 が逆元です
乗法
結合律
\begin{align*}
((a_0 + a_1 \zeta_3) \cdot (b_0 + b_1 \zeta_3)) \cdot (c_0 + c_1 \zeta_3)
&= ((a_0 b_0 - a_1 b_1) + (a_0 b_1 + a_1 b_0 - a_1 b_1) \zeta_3) \cdot (c_0 + c_1 \zeta_3) \\
&= ((a_0 b_0 - a_1 b_1)c_0 - (a_0 b_1 + a_1 b_0 - a_1 b_1)c_1) + ((a_0 b_0 - a_1 b_1)c_1 + (a_0 b_1 + a_1 b_0 - a_1 b_1)c_0 - (a_0 b_1 + a_1 b_0 - a_1 b_1)c_1) \zeta_3 \\
&= (a_0(b_0 c_0 - b_1 c_1) - a_1(b_0 c_1 + b_1 c_0 - b_1 c_1)) + (a_0(b_0 c_1 + b_1 c_0 - b_1 c_1) + a_1(b_0 c_0 - b_1 c_1) - a_1(b_0 c_1 + b_1 c_0 - b_1 c_1)) \zeta_3 \\
&= (a_0 + a_1 \zeta_3) \cdot ((b_0 c_0 - b_1 c_1) + (b_0 c_1 + b_1 c_0 - b_1 c_1) \zeta_3) \\
&= (a_0 + a_1 \zeta_3) \cdot ((b_0 + b_1 \zeta_3) \cdot (c_0 + c_1 \zeta_3))
\end{align*}
単位元
1 + 0 \cdot \zeta_3 が単位元です
分配律
\begin{align*}
\displaystyle
(a_0 + a_1 \zeta_3) \cdot ((b_0 + b_1 \zeta_3) + (c_0 + c_1 \zeta_3))
&= (a_0 + a_1 \zeta_3) \cdot ((b_0 + c_0) + (b_1 + c_1) \zeta_3) \\
&= (a_0 (b_0 + c_0) - a_1(b_1 + c_1)) + (a_0 (b_1 + c_1) + a_1 (b_0 + c_0) - a_1 (b_1 + c_1)) \zeta_3 \\
&= ((a_0 b_0 - a_1 b_1) + (a_0 b_1 + a_1 b_0 - a_1 b_1) \zeta_3) + ((a_0 c_0 - a_1 c_1) + (a_0 c_1 + a_1 c_0 - a_1 c_1) \zeta_3) \\
&= (a_0 + a_1 \zeta_3) \cdot (b_0 + b_1 \zeta_3) + (a_0 + a_1 \zeta_3) \cdot (c_0 + c_1 \zeta_3)
\end{align*}
しかし,\mathbb{Z}[\zeta_3] は体ではありません.
掛け算の逆元
以下では,\mathbb{Q}[\zeta_3] 内で考えます.つまり,係数は整数でなく有理数の値を取るものとします.
このとき,a_0 + a_1 \zeta_3 の掛け算に関する逆元は, \displaystyle \frac{a_0 - a_1}{a_0^2 - a_0 a_1 + a_1^2} + \frac{- a_1}{a_0^2 - a_0 a_1 + a_1^2} \zeta_3 になっています.実際,A = a_0^2 - a_0 a_1 + a_1^2 として,
\begin{align*}
& (a_0 + a_1 \zeta_3) \left( \frac{a_0 - a_1}{a_0^2 - a_0 a_1 + a_1^2} + \frac{- a_1}{a_0^2 - a_0 a_1 + a_1^2} \zeta_3 \right) \\
& = \frac{a_0^2 - a_0 a_1}{A} - \frac{a_0 a_1}{A} \zeta_3 + \frac{a_0 a_1 - a_1^2}{A} \zeta_3 - \frac{a_1^2}{A} \zeta_3^2 \\
& = \frac{a_0^2 - a_0 a_1}{A} - \frac{a_0 a_1}{A} \zeta_3 + \frac{a_0 a_1 - a_1^2}{A} \zeta_3 - \frac{a_1^2}{A} ( - 1 - \zeta_3) \\
& = \frac{a_0^2 - a_0 a_1 + a_1^2}{A} \\
& = 1
\end{align*}
です.よって,逆元であることが示されました.
しかし,\displaystyle \frac{a_0 - a_1}{a_0^2 - a_0 a_1 + a_1^2} や \displaystyle \frac{- a_1}{a_0^2 - a_0 a_1 + a_1^2} は整数とは限りません.
反例は死ぬほどありますが,たとえば,a_0 = 2, a_1 = 1 などが該当します.
つまり,\mathbb{Q}[\zeta_3] であれば,掛け算の逆元は存在するが,\mathbb{Z}[\zeta_3] だと,掛け算の逆元は存在しないことが一般に言えます(元々,\mathbb{Z} に掛け算の逆元が存在するとは限らないので,それはそうって感じですが).
p分整数
この章は,論文に記載されていないですが,分かりやすさのために追記しようと思います.この章では,p を素数とします.まずは抽象論をさらっと展開して,その後に具体例で突っ込んでいくスタイルでいきます.
\zeta_3 の3の部分を一般の素数に拡張してみようと思います.つまり,1の p 乗根である \zeta_p を考えてみます.
\zeta_p の値はすぐに分かりません.しかし,\displaystyle \zeta_3 = \cos \left( \frac{2 \pi}{3} \right) + \sin \left( \frac{2 \pi}{3} \right) \sqrt{-1} でしたので,\displaystyle \zeta_p = \cos \left( \frac{2 \pi}{p} \right) + \sin \left( \frac{2 \pi}{p} \right) \sqrt{-1} になりそうな気がします.いや正しいんですが.
上の予想を正当化する
まず,1の3乗根とはなんだったかっていうと,今回の「1の3乗根」 の Def に記載したとおりで,X^3 - 1 = 0 の解(のうち,1以外で最も偏角が小さいもの)でした.それを求めると,\displaystyle \zeta_3 = \frac{-1}{2} + \frac{\sqrt{3}}{2} になっていました.
すると,1の p 乗根は,X^p - 1 = 0 の解であり,1以外で最も偏角が小さいものなので,\displaystyle \zeta_p = \cos \left( \frac{2 \pi}{p} \right) + \sin \left( \frac{2 \pi}{p} \right) \sqrt{-1} と求められます.
実際,\zeta_p^p を計算しようと思うと,De Moivreの定理 から,
\begin{align*}
\displaystyle
\zeta_p^p
& = \left( \cos \left( \frac{2 \pi}{p} \right) + \sin \left( \frac{2 \pi}{p} \right) \sqrt{-1} \right )^p \\
& = \cos \left( \frac{2 \cdot p \cdot \pi}{p} \right) + \sin \left( \frac{2 \cdot p \cdot \pi}{p} \right) \sqrt{-1} \\
& = \cos (2 \pi) + \sin (2 \pi) \sqrt{-1} \\
& = 1
\end{align*}
が成り立ちます.よって,\displaystyle \cos \left( \frac{2 \pi}{p} \right) + \sin \left( \frac{2 \pi}{p} \right) \sqrt{-1} は X^p - 1 = 0 の解であることが分かりました.
また,この偏角は 2 \pi を p で割ったものですから,これより偏角が小さくて X^p - 1 = 0 の解になる(p 乗すると1になる)ような(1以外の)ものは存在しません.
よって,1の p 乗根 \zeta_p の値が分かりました.
そして,
つまり,X^3 - 1 = 0 の解は,単位円の円周上にちょうど3等分する位置に存在することになります.
1の3乗根にはこのような特徴もありました.
すると,X^p - 1 = 0 の解は,X = 1, \zeta_p, \zeta_p^2, \cdots, \zeta_p^{p - 1} の p 個であると考えられます.
上の予想を正当化する
X = 1 が X^p - 1 = 0 の解なのはいいとして,1 \leq i \leq p - 1 として,他の \zeta_3^i で表せる複素数が X^p - 1 で表せるのかを確認します.
再び,De Moivreの定理 を使うと,
\begin{align*}
\zeta_p^i
& = \left( \cos \left( \frac{2 \pi}{p} \right) + \sin \left( \frac{2 \pi}{p} \right) \sqrt{-1} \right )^i \\
& = \cos \left( \frac{2 \cdot i \cdot \pi}{p} \right) + \sin \left( \frac{2 \cdot i \cdot \pi}{p} \right) \sqrt{-1} \\
\end{align*}
と求められます.これらに対して,更に p 乗したときの値が1と一致するかどうかを調べます.
\begin{align*}
(\zeta_p^i)^p
& = \left( \cos \left( \frac{2 \cdot i \cdot \pi}{p} \right) + \sin \left( \frac{2 \cdot i \cdot \pi}{p} \right) \sqrt{-1} \right)^p \\
& = \cos \left( \frac{2 \cdot i \cdot p \cdot \pi}{p} \right) + \sin \left( \frac{2 \cdot i \cdot p \cdot \pi}{p} \right) \sqrt{-1} \\
& = \cos (2 \cdot i \cdot \pi) + \sin (2 \cdot i \cdot \pi) \sqrt{-1} \\
& = \cos (2 \pi) + \sin (2 \pi) \sqrt{-1} \\
& = 1
\end{align*}
よって,\zeta_3^i も X^p - 1 = 0 の解であることが分かりました.
また,1の3乗根でのPropのような性質もちゃんと成り立ちます.
\underline{\mathrm{Prop(1のp乗根)}}
1のp乗根 \zeta_p について,k を自然数とすると,次が成り立つ:
\begin{align*}
\zeta_p^{p - 1} & = -1 - \zeta_p - \zeta_p^2 - \cdots - \zeta_p^{p - 2} \\
\zeta_p^{pk} & = 1 \\
\zeta_p^{pk + 1} & = \zeta_p \\
\zeta_p^{pk + 2} & = \zeta_p^2 \\
\vdots \\
\zeta_p^{pk + (p - 2)} & = \zeta_p^{p - 2}
\end{align*}
以上から,p 分整数を次のように定義できます.
\underline{\mathrm{Def(p分整数)}}
a_0, a_1, \cdots, a_{p - 2} を整数とするとき,a_0 + a_1 \zeta_p + \cdots + a_{p - 2} \zeta_p^{p - 2} の形の整数をp分整数という.
p 分整数全体の集合 \{ a_0 + a_1 \zeta_p + \cdots + a_{p - 2} \zeta_p^{p - 2} \ | \ a_0, a_1, \cdots, a_{p - 2} \in \mathbb{Z} \} を \mathbb{Z}[\zeta_p] と書く.
演算の定義は3分整数とほぼ同じです.よって,\mathbb{Z}[\zeta_p] も環になっています.
*一般のp 分整数の積を明示するのはあまりにもめんどくさいので,省略します・・・
さて,少し抽象的な話になってしまったので,具体例で確認してみます.p = 7 としてみます.今まで「ここは3分整数の議論と同じで」としてきた部分も踏み込んでみます.
すると,まずは,1の7乗根 \zeta_7 に対して,\displaystyle\zeta_7 = \cos \left( \frac{2 \pi}{7} \right) + \sin \left( \frac{2 \pi}{7} \right) \sqrt{-1} です.すると,\zeta_7 は X^7 - 1 = 0 の解であり,特に,X^6 + X^5 + X^4 + X^3 + X^2 + X + 1 = 0 の解です(X^7 - 1 = (X - 1)(X^6 + X^5 + X^4 + X^3 + X^2 + X + 1) で \zeta_7 \neq 1)から,ここに X = \zeta_7 を代入することで,
\begin{align*}
\zeta_7^6 = - 1 - \zeta_7 - \zeta_7^2 - \zeta_7^3 - \zeta_7^4 - \zeta_7^5
\end{align*}
を得られます.このことから,
\begin{align*}
\zeta_7^{7k} & = 1 \\
\zeta_7^{7k + 1} & = \zeta_7 \\
\zeta_7^{7k + 2} & = \zeta_7^2 \\
\zeta_7^{7k + 3} & = \zeta_7^3 \\
\zeta_7^{7k + 4} & = \zeta_7^4 \\
\zeta_7^{7k + 5} & = \zeta_7^5
\end{align*}
も分かります.
7分整数は,a_0, \cdots, a_5 \in \mathbb{Z} を用いて,a_0 + a_1 \zeta_7 + a_2 \zeta_7^2 + a_3 \zeta_7^3 + a_4 \zeta_7^4 + a_5 \zeta_7^5 と表せるので,
\begin{align*}
\mathbb{Z}[\zeta_7] = \{ a_0 + a_1 \zeta_7 + a_2 \zeta_7^2 + a_3 \zeta_7^3 + a_4 \zeta_7^4 + a_5 \zeta_7^5 \ | \ a_0, a_1, \cdots, a_5 \in \mathbb{Z} \}
\end{align*}
となります.
m分整数
前章では素数 p に限定して考えましたが,以下では一般の整数 m について考察します.
ただ,いきなり一般論から入ると難しいかなと思うので,今回は m = 6 の例を先にやります.
今までの話から,1の6乗根 \zeta_6 は
\begin{align*}
\displaystyle \zeta_6 = \cos \left( \frac{2 \pi}{6} \right) + \sin \left( \frac{2 \pi}{6} \right) \sqrt{-1} = \frac{1}{2} + \frac{\sqrt{3}}{2} \sqrt{-1}
\end{align*}
になります.そして,自然数 k を使って,
\begin{align*}
\zeta_6^5 &= - 1 - \zeta_6 - \cdots - \zeta_6^4 \\
\zeta_6^{6k} & = 1 \\
\zeta_6^{6k + 1} & = \zeta_6 \\
\zeta_6^{6k + 2} & = \zeta_6^2 \\
\zeta_6^{6k + 3} & = \zeta_6^3 \\
\zeta_6^{6k + 4} & = \zeta_6^4
\end{align*}
も成り立ちます.ここで,なぜ3分整数やp分整数に \zeta_3^2 や \zeta_p^{p - 1} の項が含まれなかったのかを考えると,他の項の和で表すことができる(1次従属)からでした.\zeta_3^2 = - 1 - \zeta_3 のように.
では,m = 6 の場合を考えると,実は,\zeta_6^2 = - 1 + \zeta_6 と表すことができます.それだけではなく,\zeta_6^3 = -1 ですし,\zeta_6^4 = - \zeta_6 です.
実際,
\begin{align*}
\displaystyle
\zeta_6^2 & = \cos \left( \frac{2 \cdot 2 \pi}{6} \right) + \sin \left( \frac{2 \cdot 2 \pi}{6} \right) \sqrt{-1} = \cos \left( \frac{4 \pi}{6} \right) + \sin \left( \frac{4 \pi}{6} \right) \sqrt{-1} = - \frac{1}{2} + \frac{\sqrt{3}}{2} \sqrt{-1} = - 1 + \zeta_6 \\
\zeta_6^3 & = \cos \left( \frac{2 \cdot 3 \pi}{6} \right) + \sin \left( \frac{2 \cdot 3 \pi}{6} \right) \sqrt{-1} = \cos \left( \frac{6 \pi}{6} \right) + \sin \left( \frac{6 \pi}{6} \right) \sqrt{-1} = -1 \\
\zeta_6^4 & = \cos \left( \frac{2 \cdot 4 \pi}{6} \right) + \sin \left( \frac{2 \cdot 4 \pi}{6} \right) \sqrt{-1} = \cos \left( \frac{8 \pi}{6} \right) + \sin \left( \frac{8 \pi}{6} \right) \sqrt{-1} = - \frac{1}{2} - \frac{\sqrt{3}}{2} \sqrt{-1} = - \zeta_6 \\
\end{align*}
です.
つまり,1, \zeta_6 さえあれば,\zeta_6^2, \zeta_6^3, \zeta_6^4 も表現できることが分かりました.
では一般の整数 m に拡張してみましょう.
1のm乗根 \zeta_m は \displaystyle \zeta_m = \cos \left( \frac{2 \pi}{m} \right) + \sin \left( \frac{2 \pi}{m} \right) \sqrt{-1} になります.そして,自然数 k を使って,
\begin{align*}
\zeta_m^{m - 1} &= - 1 - \zeta_m - \cdots - \zeta_m^{m - 2} \\
\zeta_m^{mk} & = 1 \\
\zeta_m^{mk + 1} & = \zeta_m \\
\zeta_m^{mk + 2} & = \zeta_m^2 \\
\vdots \\
\zeta_m^{mk + (m - 2)} & = \zeta_m^{m - 2}
\end{align*}
も成り立ちます.
では,問題の \zeta_m^i は他の 1, \zeta_m, \cdots を使って表せるのかという問題についてですが,実はこれらについて綺麗な理論が知られています.
まず,オイラー関数というものを導入します.
\underline{\mathrm{Def(オイラー関数)}}
m を正整数とするとき,\phi(m) で m - 1 以下で m と互いに素な正整数の個数を表す.
例えば,m = 6 を考えると,5以下の正整数で6と互いに素なものは 1,5 ですので,\phi(6) = 2 です.また,m が素数 p のとき,素数の定義から \phi(p) = p - 1 となります.実際,\phi(3) = 2 です.
これらの結果を見ると,今までの例で,いくつの 1, \zeta_m, \cdots を用いれば,\zeta_m^i をそれらの足し算とスカラー倍で表せるのか,という問いにたいして,\phi(m) 個と答えることができます.
そこで,m - 1 未満で m と互いに素(coprime)な正整数の集合を cp(m) = \{ c_1, \cdots, c_{n - 1} \} と表すことにします.n = \phi(m) で,c_i < c_{i + 1} です.
すると,cp(m) に属さない m - 1 未満の正整数 i について,
\begin{align*}
\zeta_m^i = a_0 \zeta_m^{0} + a_1 \zeta_m^{c_1} + \cdots + a_{n - 1} \zeta_m^{c_{n - 1}}
\end{align*}
なる整数の組 (a_0, a_1, \cdots, a_{n - 1}) が存在します.
*cp(m) = \{ c_1, \cdots, c_{n - 1} \} の要素数は n - 1 であることに注意してください,つまり,m - 1 \notin cp(m) です,これは,\zeta_m^{m - 1} = - 1 - \zeta_m - \cdots - \zeta_m^{m - 2} から除いています
もう少し詳しい理論としては,\phi(m) は次数 m の円分多項式の根の数に対応して,それらの根は1の原始 m 乗根であることが知られています.
原始n乗根
\underline{\mathrm{Def(n乗根と原始n乗根, nth \ root \ and \ primitve \ nth \ root)}}
n を正整数とするとき,z \in \mathbb{C} であって,z^n = 1 を満たす z を1の n 乗根という.
\zeta が1の n 乗根であり,0 < m < n で \zeta^m \neq 1 を満たすとき,\zeta を1の原始 n 乗根という.
よく見る i = \sqrt{-1} は1の4乗根であり,1の原始4乗根です.しかし,1の8乗根でもありますが,1の原始8乗根ではありません.
円分多項式
\underline{\mathrm{Def(円分多項式, cyclotomic \ polynomial)}}
n を正整数,\zeta_n \in \mathbb{C} を1の原始 n 乗根とするとき,n 次の円分多項式 \Phi_n(X) は次のように表せる:
\begin{align*} \displaystyle
\Phi_n(X) = \prod_{1 \leq i \leq n, iとnは互いに素} (X - \zeta_n^i)
\end{align*}
いかつい形をしていますが,なんと \Phi_n(X) は任意の n で整数係数の既約多項式であることが知られています.
少し計算をしてみると,例えば,n = 3 のとき,
\begin{align*} \displaystyle
\Phi_3(X) &= (X - \zeta_3^1)(X - \zeta_3^2) = (X - e^{\frac{2 \pi \sqrt{-1}}{3}})(X - e^{\frac{4 \pi \sqrt{-1}}{3}}) \\ &= (X - (- \frac{1}{2} + \frac{\sqrt{3}}{2} \sqrt{-1}))(X - (- \frac{1}{2} - \frac{\sqrt{3}}{2} \sqrt{-1})) = X^2 + X + 1
\end{align*}
となり,n = 4 では,
\begin{align*} \displaystyle
\Phi_4(X) &= (X - \zeta_4^1)(X - \zeta_4^3) = (X - \sqrt{-1})(X - \sqrt{-1}^3) = (X - \sqrt{-1})(X + \sqrt{-1}) \\
&= X^2 + 1
\end{align*}
となります.
さて,以上の結果を踏まえると,m 分整数は次のようにして定められます.
\underline{\mathrm{Def(m分整数)}}
正整数 m に対して,n = \phi(m) として,m - 1 未満で m と互いに素な正整数全体の集合を cp(m) = \{ c_1, \cdots, c_{n - 1} \} とする.ただし,cp(m) の要素は昇順であるとする.
このとき,a_0, a_1, \cdots, a_{n - 1} を整数とするとき,a_0 \zeta_m^{0} + a_1 \zeta_m^{c_1} + \cdots + a_{n - 1} \zeta_m^{c_{m - 1}} の形の整数を m 分整数という.
m 分整数全体の集合 \{ a_0 \zeta_m^{0} + a_1 \zeta_m^{c_1} + \cdots + a_{n - 1} \zeta_m^{c_{m - 1}} \ | \ a_0, a_1, \cdots, a_{n - 1} \in \mathbb{Z} \} を \mathbb{Z}[\zeta_m] と書く.
p 分整数のときは,a_i のインデックスが p - 2 で終わっていたのに対して,こちらは n - 1 であることに違和感がある方もいらっしゃるかもしれませんが,\phi(p) = p - 1 なので,n = p - 1 と置くと,n - 1 = (p - 1) - 1 = p - 2 なので整合性が取れています.
イデアル
さて,いよいよ「イデアル格子暗号」のイデアルに注目します.ここも初めは少し抽象的な話が続きますが,最後に具体例を取り上げてもう一度振り返ることにします.
\underline{\mathrm{Def(イデアル)}}
m 分整数 g = g_0 + g_1 \zeta_n + \cdots + g_{n - 1} \zeta_n^{n - 1} に対して,次の集合 I_g をイデアルという:
\begin{align*}
I_g = \{ a_0 g + a_1 \zeta_n g + \cdots + a_{n - 1} \zeta_n^{n - 1} g \ | \ a_0, a_1, \cdots, a_{n - 1} \in \mathbb{Z} \}
\end{align*}
I_g は和とスカラー倍で閉じています.これを証明しましょう.
上記の証明
a_0, a_1, \cdots, a_{n - 1}, g_0, g_1, \cdots, g_{n - 1} \in \mathbb{Z} に対して,
\begin{align*}
\displaystyle
& a_0 + a_1 \zeta_n g + \cdots + a_{n - 1} \zeta_n^{n - 1} g \\
& = a_0 + a_1 \zeta_n (g_0 + g_1 \zeta_n + \cdots + g_{n - 1} \zeta_n^{n - 1}) + \cdots + a_{n - 1} \zeta_n^{n - 1} (g_0 + g_1 \zeta_n + \cdots + g_{n - 1} \zeta_n^{n - 1}) \\
& = (a_0 + a_1 g_{n - 1} + \cdots + a_{n - 1} g_1) + (a_1 g_0 + a_2 g_{n - 1} + \cdots + a_{n - 1} g_2) \zeta_n + \cdots + (a_1 g_{n - 2} + a_2 g_{n - 3} + \cdots + a_{n - 1} g_0) \zeta_n^{n - 1} \\
& = \left( a_0 + \sum_{i = 1}^{n - 1} a_i g_{n - i} \right) + \left( a_1 g_0 + \sum_{i = 2}^{n - 1} a_i g_{n + 1 - i} \right) \zeta_n + \cdots + \left( \sum_{i = 1}^n a_i g_{n - 1 - i} \right) \zeta_n^{n - 1} \\
\end{align*}
です.
和で閉じている
a_0, a_1, \cdots, a_{n - 1}, b_0, b_1, \cdots, b_{n - 1}, g_0, g_1, \cdots, g_{n - 1} \in \mathbb{Z} に対して,
\begin{align*}
& (a_0 + a_1 \zeta_n g + \cdots + a_{n - 1} \zeta_n^{n - 1} g) + (b_0 + b_1 \zeta_n g + \cdots + b_{n - 1} \zeta_n^{n - 1} g) \\
& = \left( a_0 + \sum_{i = 1}^{n - 1} a_i g_{n - i} \right) + \left( a_1 g_0 + \sum_{i = 2}^{n - 1} a_i g_{n + 1 - i} \right) \zeta_n + \cdots + \left( \sum_{i = 1}^n a_i g_{n - 1 - i} \right) \zeta_n^{n - 1} + \left( b_0 + \sum_{i = 1}^{n - 1} b_i g_{n - i} \right) + \left( b_1 g_0 + \sum_{i = 2}^{n - 1} b_i g_{n + 1 - i} \right) \zeta_n + \cdots + \left( \sum_{i = 1}^n b_i g_{n - 1 - i} \right) \zeta_n^{n - 1} \\
& = \left( (a_0 + b_0) + \sum_{i = 1}^{n - 1} (a_i + b_i) g_{n - i} \right) + \left( (a_1 + b_1) g_0 + \sum_{i = 2}^{n - 1} (a_i + b_i) g_{n + 1 - i} \right) \zeta_n + \cdots + \left( \sum_{i = 1}^n (a_i + b_i) g_{n - 1 - i} \right) \zeta_n^{n - 1} \\
\end{align*}
であり(3行目の等号は \mathbb{Z}[\zeta_n] で定義されている足し算),係数は全て整数なので,これは成り立ちます.
スカラー倍で閉じている
a_0, a_1, \cdots, a_{n - 1}, g_0, g_1, \cdots, g_{n - 1}, c_0, c_1, \cdots, c_{n - 1} \in \mathbb{Z} に対して,
\begin{align*}
& (c_0 + c_1 \zeta_n + \cdots + c_{n - 1} \zeta_n^{n - 1})(a_0 + a_1 \zeta_n g + \cdots + a_{n - 1} \zeta_n^{n - 1} g) \\
& = (c_0 + c_1 \zeta_n + \cdots + c_{n - 1} \zeta_n^{n - 1}) \left( a_0 + \sum_{i = 1}^{n - 1} a_i g_{n - i} \right) + (c_0 + c_1 \zeta_n + \cdots + c_{n - 1} \zeta_n^{n - 1}) \left( a_1 g_0 + \sum_{i = 2}^{n - 1} a_i g_{n + 1 - i} \right) \zeta_n + \cdots + (c_0 + c_1 \zeta_n + \cdots + c_{n - 1} \zeta_n^{n - 1}) \left( \sum_{i = 1}^n a_i g_{n - 1 - i} \right) \zeta_n^{n - 1} \\
\end{align*}
であり(後の整理はめんどくさいので省略),係数は全て整数なので,これは成り立ちます.
以上より示されました.
もっと一般的なイデアルの定義
「もっと一般的」って書いていますが,通常の可換環に対する定義です.群を扱う際にそれよりも「小さいスケール」である部分群を考えることがあります.環でも同じようなことを考えるのですが,部分環だと制約が大きい(掛け算で閉じる,が難しい)ので,それよりも少し緩いイデアルというものを考えることが多いです.
\underline{\mathrm{Def(イデアル, ideal)}}
R を可換環,I を R の部分集合とするとき,I が R のイデアルとは,次の2つの条件を満たすことである:
\begin{align*}
& \bullet \ a, b \in I \Rightarrow a + b \in I \\
& \bullet \ a \in I, c \in R \Rightarrow ac (= ca) \in I \\
\end{align*}
まとめると,イデアルは,環の部分集合であって,
今,I_g は環 \mathbb{Z}[\zeta_n] の部分集合であって(\mathbb{Z}[\zeta_n] が環であることは,今回の「m分整数」 で見ています),
これは,1, \zeta_n, \cdots, \zeta_n^{n - 1} で張られていた「格子」を g, g \zeta_n, \cdots, g \zeta_n^{n - 1} で張られる「格子」に取り替えることに対応します.
*線型代数に慣れている方向けだと,\mathbb{Z}[\zeta_n] の基底 \{1, \zeta_n, \cdots, \zeta_n^{n - 1}\} を \{ g, g \zeta_n, \cdots, g \zeta_n^{n - 1} \} に取り替えています
つまり,「感覚的には」今まで a_0 + a_1 \zeta_n で考えていたベクトルを適当な整数 b_0, b_1 を使って,b_0 g + b_1 (g \zeta_n) で取り替えることを表しています.
もちろん全てのベクトルを取り替えられるわけではありませんし,上では2次元の場合しか考えていませんが,n - 1 次元の場合でも同様です.
これを表した図が論文に記載されているので,こちらを掲載します.
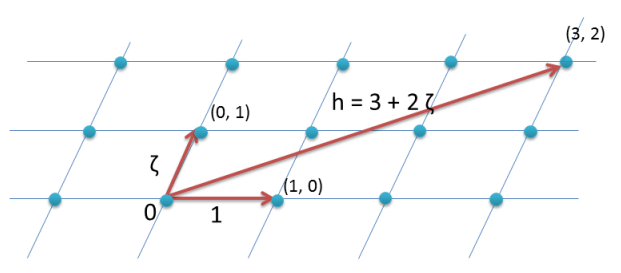
では,最後に具体例をやります.
m = 3 として,\displaystyle \zeta_3 = \frac{-1}{2} + \frac{\sqrt{3}}{2} を考えます.要するに1の3乗根です.
ここで,g = 3 + 4 \zeta_3 とすると,I_g = \{ a_0 + a_1 \zeta_3 + g \ | \ a_0, a_1 \in \mathbb{Z} \} となります.\zeta_3 g = - 4 - \zeta_3 です.
例えば,- 6 + 5 \zeta_3 を考えましょう.これは当然,1, \zeta_3 で貼られる格子点 (-6, 5) 上に存在します.
ここで,- 6 + 5 \zeta_3 = 2 (3 + 4 \zeta_3) + 3(- 4 - \zeta_3) = 2 g + 3 g \zeta_3 が成り立っていますから,これは - 6 + 5 \zeta_3 は g, g \zeta_3 で貼られる格子状では (2, 3) なる格子点上に存在することが分かります.
よって,同じ - 6 + 5 \zeta_3 でも 1, \zeta_3 で見るか,g, g \zeta_3 で見るか,で格子点(つまり座標)が異なることが分かりました.
この「同じ点をどの格子で考えるか」という視点が次の章で非常に効いてきます.
衝突困難関数とSVP
この章では,次の暗号理論への応用として,前章の円分整数が関係するNP困難な問題について考察します.
まずは,衝突困難関数についてです.
\underline{\mathrm{Def(衝突困難関数)}}
V, W を |V| > |W| なる有限集合とする.関数 H : V \rightarrow W とする.
このとき,H(v_1) = H(v_2) かつ v_1 \neq v_2 なる v_1, v_2 を求めることがNP困難な関数 H を衝突困難関数という.
まず,H(v_1) = H(v_2) かつ v_1 \neq v_2 なる v_1, v_2 が存在するのか,ということが気になりますが,これは問題ありません.V の |W| + 1 個の元について調べればいいからです.
上記の証明
鳩の巣原理を使って証明します.
部分集合 V^{\prime} \subset V かつ |V^{\prime}| = W + 1 を取ります.このとき,|V| > |W| ですから,|V| \geq |W| + 1 なので,このような V^{\prime} は存在します.
このとき,V^{\prime} = \{ v_1, v_2, \cdots, v_{|W| + 1} \} として,これらの元を H で W に送った集合 H(V^{\prime}) = \{ H(v_1), H(v_2), \cdots, H(v_{|W| + 1}) \} を考えます.このとき,H(V^{\prime}) \subset W ですが,|H(V^{\prime})| = |W + 1| なので,H(V^{\prime}) のなかに重複する元が存在します.そうでないとすると,W の中に相異なる元が |W| + 1 個存在することになり,H(V^{\prime}) \subset W に矛盾するからです.
よって証明されました.
ここで,NP困難というには何かしら根拠が必要で,今回は別のNP困難な問題を元にしています.それがSVPと呼ばれる問題で,ここで円分整数が関係してきます.
\underline{\mathrm{Def(最短円分整数問題)}}
自然数 m を取って,n = \phi(m) とする.f_0, \cdots, f_{n - 1} \in \mathbb{Z} として f = f_0 + f_1 \zeta_m + \cdots + f_{n - 1} \zeta_m^{n - 1} と置く.イデアル I_f と 0ではない円分整数 g = a_0 f + a_1 \zeta_m f + \cdots + a_{n - 1} \zeta_m^{n - 1} f \in I_f \ (a_0, \cdots, a_{n - 1} \in \mathbb{Z}) が与えられているとする.
このとき,c_0, \cdots, c_{n - 1} \in \mathbb{Z} で g = c_0 + c_1 \zeta_m + \cdots + c_{n - 1} \zeta_m^{n - 1} であって,g の大きさ ||g|| = \sqrt{c_0^2 + c_1^2 + \cdots + c_{n - 1}^2} が最小な (c_0, \cdots, c_{n - 1}) を求めよ.
*どちらかというと,最近円分整数問題のような気がしますが・・・以下では,Shortest Vector Problem ということで,SVPと省略します
では,上記のSVPを用いて,どのようにして衝突困難関数を構成にするのかについてですが,あまりに長くなりそうなので,別の記事で紹介します・・・.
今回の内容はここまでです.ここまでご覧になってくださった方々ありがとうございます!




Discussion