今回出てくる予備知識のまとめ
Appendix A : Complexity Assumptions Over the Real Torus
- TLWEとTRLWE
3章前説
- 3章の流れ
- ギリシャ文字と花文字
- $\hat{\mathbb{Z}}$ と $\hat{\mathbb{T}}$
- 3章前説の議論
- 3章前説の議論の考察
3.1 Encoding/Decoding Messages
- lift
- Upper
- 3.1の議論
- 3.1の議論の考察

第2.5回（番外編）

なぜ番外編が必要なのか
今回出てくる予備知識のまとめ
GGSW方式とは
無限ノルム
Tensor積
gadget行列
gadget decomposition
GGSW方式のアルゴリズム
GGSW方式のアルゴリズムの具体例
これまでの議論の考察１
GGSW方式の暗号文の足し算
GGSW方式の暗号文同士の内積
これまでの議論の考察２

第３回

今回出てくる予備知識のまとめ
3.2 Description
- TFHE方式のアルゴリズム
- TFHE方式のアルゴリズムの具体例
- 無限ノルム
- TFHE方式のアルゴリズムの正当性
- 3.2の議論の考察
3.3 Leveled Operation
- Tensor積
- gadget行列
- gadget decompostion
- GGSW方式の概要
- TFHE方式の暗号文の足し算
- TFHE方式の暗号文のスカラー倍
- 結局 Leveled Operaion とは何か
- TFHE方式の暗号文とGGSW方式の暗号文の外積
- Cmuxゲート
- 3.3の議論の考察

第４回（イマココ）

４章の流れ
4.1 Blind Rotation
- 4.1でやりたいこと
- Rescaling
- bootstrapでやりたいこと
- Blind Rotation
- Sample Extraction
- Key Swicthing
- bootstrapのまとめ
- 4.1の議論の考察
4.2 Look-up Table Evaluation
- 4.2の議論
- 4.2の議論の考察

今回は第４回目で，
4 Programmable Bootstrapping
4.1 Blind Rotation
4.2 Look-up Table Evaluation
理論編ラストです．最後までボリュームたっぷりです．

具体的な内容としては，次のようになります:

４章の流れ
4.1 Blind Rotation
- 4.1でやりたいこと
- Rescaling
- bootstrapでやりたいこと
- Blind Rotation
- Sample Extraction
- Key Swicthing
- bootstrapのまとめ
- 4.1の議論の考察
4.2 Look-up Table Evaluation
- 4.2の議論
- 4.2の議論の考察

今回の「４章の流れ」で詳しいことは触れますが，今回は，暗号文から平文への効率的な復号法（＝bootstrap）を4.1で解説し，前回の Leveled Operations と今回の bootstrap を組合わせて，4.2での本論文メインとなり programmable bootstrap を解説します．

４章の流れ

４章に入ります．
４章では，暗号文からノイズを取り除くことがメインで，これを bootstrap と言います．TLWE/TRLWE方式の暗号文同士の演算ができるかどうかは，ノイズによって定まるのでした．そこで，ノイズを取り除くことで，Leveled Operation を実行できます．
4.1：bootstrap
4.2：programmable bootstrap
4.1のタイトルが「Blind Rotation」になっていますが，これは bootstrap で使うアルゴリズムの1つです（~~Blind Rotation っていう名前の bootstrap の手法だと思っていました~~）．それとは別に Sample Extraction と Key Switching というアルゴリズムも使用します．これら Blind Rotation と Sample Extraction, Key Switching を順に合成したアルゴリズムが bootstrap です．これらのアルゴリズムを定義する際に，3.3 の Leveled Operations が必要になります．
そして，上記の bootstrap を使って暗号文へ任意の演算を作用させることができる手法が，4.2 で解説する programmable bootstrap です．

ちなみに４章で具体例を扱うと思うと，めちゃめちゃ計算がうるさいので，今回は具体例は省略します・・・（サイレント補筆するかもです）．その代わり？，式変形は丁寧にやるつもりです．

4.1でやりたいこと

今回は始めに状況設定を共通で行いたいので，議論パートを先に持ってきます．各アルゴリズムの細かい話を各論でやっていきます．

状況設定としては，第３回「TFHE方式のアルゴリズム」でやったアルゴリズムが必要になります．

始めにKeyGenからです．
始めに， $k$ は1以上の自然数， $\sigma$ は任意の（正の）実数， $\bar{w}, w, \Omega$ は全て正整数で， $\bar{w} + w \leq \Omega$ を満たす，ものとします．

＊論文の $n$ は上記の　 $k$ に相当しますが，変更する意味がないので $k$ で解説します

次に， $\chi$ を $\mathbb{R}_N[X]$ 上の正規分布で， $\mathcal{N}(0, \sigma^2)$ として， $p = 2^{\bar{w} + w}, \ q = 2^{\Omega}$ とします．
また，秘密鍵は， $s = (s_0, s_1, \cdots, s_{k - 1}) \overset{\#}{\leftarrow} \mathbb{B}^k$ です．
最後に，平文空間 $\tilde{P}$ を $\displaystyle \tilde{P} = (\frac{q}{p} \mathbb{Z} / q \mathbb{Z}) \subset \hat{\mathbb{Z}} = (\mathbb{Z} / q \mathbb{Z})$ と定めます．

＊ $\tilde{\cdot}$ 記号は多項式を表すことに注意してください，今は多項式ではないので，外しています

このとき，公開鍵 $pk$ を $pk = (k, \sigma, p, q)$ で秘密鍵 $sk$ を $sk = s$ とします．

続いてEncryptです．
$(a_1, a_2, \cdots, a_k) \overset{\#}{\leftarrow} \hat{\mathbb{Z}}^k$ と各係数が $\chi$ に従うノイズ $\tilde{e} \overset{\#}{\leftarrow} \mathbb{R}$ を取る．ノイズ $e$ を $\lfloor e q \rceil$ で離散化した $e^{\prime}$ を取る．

$\hat{\mathbb{Z}} = \mathbb{Z} / q \mathbb{Z}$ 内での計算で $\displaystyle c = \sum_{j = 1}^k s_j a_j + \mu + e^{\prime} \in \hat{\mathbb{Z}}$ を求める．

$C = (a_1, a_2, \cdots, a_k, c) \in \hat{\mathbb{Z}}^{k + 1}$ とする． $C$ を $\overline{\textrm{TFHE-TLWE}}_{s}(\mu)$ と書くことにする．

そして， $C$ から $\mu$ への Decrypt は次のようになるのでした．今回考えるべきところはここです．

$\hat{\mathbb{Z}} = \mathbb{Z} / q \mathbb{Z}$ 内での計算で $\mu + e^{\prime} = c - \sum_{j = 1}^k s_j a_j$ を求める．

$\mathrm{Upper}_{q, p}(\mu + e^{\prime})$ が $\mu$ と一致する．

さて，ここまでが状況設定です．

簡単のため， $\mu^{\ast} = \mu + e^{\prime}$ と置きます．つまり， $\displaystyle - \mu^{\ast} = - (c - \sum_{j = 1}^k s_j a_j) = -c + \sum_{j = 1}^k s_j a_j$ $\in \mathbb{Z} / q \mathbb{Z}$ です．今， $- \mu \in \mathbb{Z} / q \mathbb{Z}$ とさらっと書きましたが，値は $[0, q - 1]$ に制限していることに注意してください．

$\mathrm{Upper}_{q, p}(\mu + e^{\prime})$ が $\mu$ と一致する．

から， $\mathrm{Upper}_{q, p}(\mu^{\ast}) = \mu$ になっています．

ここで，test polynomial というものを考えます．

$\underline{\mathrm{Def(test \ polynomial)}}$
任意の $i \in [0, q - 1]$ に対して， $v_i = \mathrm{Upper}_{q, p}(i) \in \mathbb{Z} / q \mathbb{Z}$ として，

\begin{align*} \tilde{v} = v_0 + v_1 X + \cdots + v_{q - 1} X^{q - 1} \end{align*}

なる $\tilde{v}$ を test polynomial という．

やりたいこととしては， $- \mu^{\ast} \in \mathbb{Z} / q \mathbb{Z}$ ですから，

\begin{align*} & X^{- \mu^{\ast}} \cdot \tilde{v} \\ & = X^{- \mu^{\ast}} \cdot (v_0 + v_1 X + \cdots + v_{\mu^{\ast} - 1} X^{\mu^{\ast} - 1} + v_{\mu^{\ast}} X^{\mu^{\ast}} + v_{\mu^{\ast} + 1} X^{\mu^{\ast} + 1} + \cdots + v_{q - 1} X^{q - 1}) \\ & = v_{\mu^{\ast}} + v_{\mu^{\ast} + 1} X + \cdots v_{q - 1} X^{q - 1 - \mu^{\ast}} + v_0 X^{q - \mu^{\ast}} + v_1 X^{q + 1 - \mu^{\ast}} + \cdots + v_{\mu^{\ast} - 1} X^{q - 1} \end{align*}

となります．何をやっているのかというと，元々 $\tilde{v}$ の中に，先頭から $\mu^{\ast} + 1$ 番目に求めたい $\tilde{v}_{\mu^{\ast}} = \mathrm{Upper}_{q, p}(\mu^{\ast})$ が格納されているのが， $X^{- \mu^{\ast}} \cdot v$ だと，先頭に $\tilde{v}_{\mu^{\ast}}$ が格納されているので，求めやすい（定数項を見るだけでいい），ということです．

そして， $X^{- \mu^{\ast}} \cdot \tilde{v}$ さえ求められれば，その先頭に求めたいものが出てくる，というのは，Decrypt での

$\hat{\mathbb{Z}} = \mathbb{Z} / q \mathbb{Z}$ 内での計算で $\mu + e^{\prime} = c - \sum_{j = 1}^k s_j a_j$ を求める．
$\mathrm{Upper}_{q, p}(\mu + e^{\prime})$ が $\mu$ と一致する．

を達成したことになります．

上手くいきましたね，めでたしめでたし．

と言うとでも思ったか・・・？
実は先ほどの議論には問題点があります．大雑把には合ってるんですけどね．

そして， $X^{- \mu^{\ast}} \cdot \tilde{v}$ さえ求められれば，その先頭に求めたいものが出てくる

の部分の $X^{- \mu^{\ast}} \cdot \tilde{v}$ を求める箇所に３つ問題があります．この３つをこれから詰めます．

test polynomial $\tilde{v}$ の定義域は？
$X^{- \mu^{\ast}}$ の定義域は？
秘密鍵はそのままでいいのか？

以降ではこれらの問題を考えます．

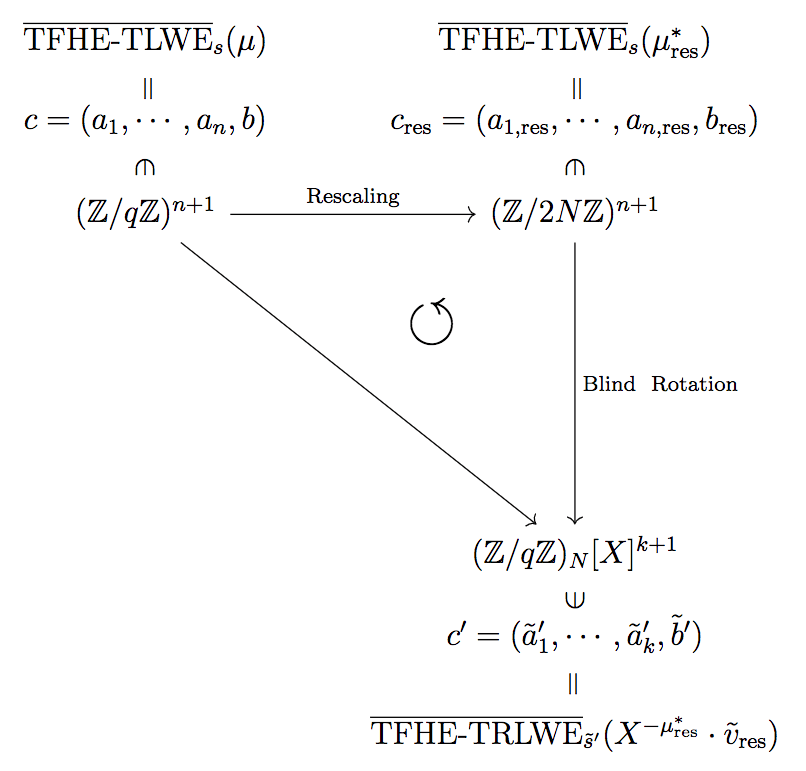
Rescaling

ここでは，

test polynomial $\tilde{v}$ の定義域は？

$X^{- \mu^{\ast}}$ の定義域は？

の2つについて考えます．まず，１つ目ですが，順当に考えたら， $\tilde{v} = v_0 + v_1 X + \cdots + v_{q - 1} X^{q - 1}$ でありますから， $\tilde{v} \in \hat{\mathbb{Z}}[X] / (X^q + 1)$ であってほしいわけです．
しかし，TFHE方式の暗号化アルゴリズムやGGSW方式の暗号化アルゴリズムであったように，暗号文空間の定義域は $\hat{\mathbb{Z}}_N[X] = \hat{\mathbb{Z}}[X] / (X^N + 1)$ でした．

参照
第３回「TFHE方式のアルゴリズム」

第2.5回「GGSW方式のアルゴリズム」

つまり， $\tilde{v}$ を何かしらで変換して $\tilde{v}^{\prime}$ のような多項式にして， $\tilde{v}^{\prime} \in \hat{\mathbb{Z}}_N[X]$ であることを考えます．
実際にどのようにして変換するかは，後に解説します．

次に，２つ目ですが， $X^{- \mu^{\ast}}$ は修正した test polynomial $\tilde{v}^{\prime}$ に作用させたいので，こちらも $X^{- \mu^{\ast}} \in \hat{\mathbb{Z}}_N[X]$ と考えるのが自然でしょう．
そこで，よくよく考えたいこととして $X^{- \mu^{\ast}}$ は $X^{\mu^{\ast}}$ の逆元でした．つまり， $X^{\mu^{\ast}}$ の逆元をどのように表すかを考えていきます．

$X^{- \mu^{\ast}} \in \hat{\mathbb{Z}}_N[X]$ ですから $X^{\mu^{\ast}} \in \hat{\mathbb{Z}}_N[X]$ なので，ここで， $\hat{\mathbb{Z}}_N[X]$ を深く考えていきます．つまり， $\hat{\mathbb{Z}}_N[X]$ での $X$ の指数の周期を考えます．
これは， $2 N$ 次の円分多項式が $X^N + 1$ であることから， $X^N = -1$ であり，また， $\hat{\mathbb{Z}}_N[X] = \hat{\mathbb{Z}}[X] / (X^N + 1)$ の $X$ の指数の周期は $2 N$ です．

参照：第１回「既約多項式と円分多項式」

2N 次の円分多項式

正式な定義の方で説明します．

参照：第１回「既約多項式と円分多項式」の折り畳み

$\underline{\mathrm{Def(原始n乗根を用いた円分多項式, cyclotomic \ polynomial)}}$
$n$ を正整数， $\zeta_n \in \mathbb{C}$ を1の原始 $n$ 乗根とするとき， $n$ 次の円分多項式 $\Phi_n(X)$ は次のように表せる:

\begin{align*} \displaystyle \Phi_n(X) = \prod_{1 \leq i \leq n, iとnは互いに素} (X - \zeta_n^i) \end{align*}

であって， $N$ は2べきなので， $2 N$ 以下の整数で $2 N$ と互いに素な整数は $N$ 個です．これは， $2 N$ と互いに素な整数は奇数ですから， $2 N$ の半分で $N$ 個であることから分かります．
よって， $2 N$ 次の円分多項式 $\Phi_{2 N}(X)$ は $\displaystyle \Phi_{2 N}(X) = \prod_{1 \leq i \leq 2 N, iと2 Nは互いに素} (X - \zeta_{2 N}^i)$ であって， $i$ の候補は $N$ 個であることから， $\mathrm{deg}(\Phi_{2 N}(X)) = N$ です．

例えば， $N = 8$ のとき， $2 N = 16$ 以下の整数で16と互いに素な整数は $1, 3, 5, 7, 9, 11, 13, 15$ の8つです．このとき，1の原始16乗根を $\zeta_{16}$ と表すと， $\zeta_{16}, \zeta_{16}^3, \zeta_{16}^5, \zeta_{16}^7, \zeta_{16}^9, \zeta_{16}^{11}, \zeta_{16}^{13}, \zeta_{16}^{15}$ は全て　 $X^{16} - 1$ の根であり，特に，「全て」1の原始16乗根です．

そして，前半の $X^N = -1$ について．
上記の $\zeta_{2 N}^i$ に関して， $\zeta_{2 N}^i$ は $X^{2 N} - 1$ の根，つまり， $X^{2 N} - 1 = 0$ の解なので， $(\zeta_{2 N}^i)^{2 N} - 1 = 0$ です．よって， $(\zeta_{2 N}^i)^{2 N} = 1$ が成り立ちます．
すると， $((\zeta_{2 N}^i)^{N})^2 = 1$ ですから， $(\zeta_{2 N}^i)^{N} = -1$ と分かります．

後半の周期について．
詳細は省きますが， $2 N$ 次の円分多項式 $\Phi_{2 N}(X)$ は $X^{2 N} - 1$ を割り切ります．
$X^{2 N} - 1 = (X^N + 1)(X^N - 1)$ で $N$ は2べきですから， $X^N - 1 = (X^{N / 2} + 1)(X^{N / 2} - 1)$ なので， $X^N - 1$ は既約多項式ではありませんから， $X^N + 1$ が既約多項式で $\Phi_{2 N}(X) = X^N + 1$ を得ます．

つまり， $X^{2 N - \mu^{\ast}} = X^{- \mu^{\ast}} \in \hat{\mathbb{Z}}_N[X]$ が成り立ちます． $X$ の指数部分は $\mathrm{mod} \ 2 N$ で考えればよいわけです．

しかし，肝心の $\mu^{\ast}$ は $\mu^{\ast} \in \mathbb{Z} / q \mathbb{Z}$ ですので， $\mathrm{mod} \ 2 N$ に収まっていませんから，ここも調整する必要があります．これは， $\displaystyle - \mu^{\ast} = - b + \sum_{j = 1}^n s_j a_j$ で $a_j, \ b \in \mathbb{Z} / q \mathbb{Z}$ であることから， $\mu^{\ast}$ を変えるには $a_j, \ b$ を変更する必要があります．

$a_j, \ b \in \mathbb{Z} / q \mathbb{Z}$ を $a_j^{\prime}, \ b^{\prime} \in \mathbb{Z} / 2 N \mathbb{Z}$ に変換するには，単純に $\cfrac{2 N}{q}$ 倍すればいい訳です．つまり， $\displaystyle a_{j, \textrm{res}} = \left \lfloor \frac{2 N a_j}{q} \right \rceil, \ b_{\textrm{res}} = \left \lfloor \frac{2 N b}{q} \right \rceil$ で実現できます．

＊res は restrict の略称で使っています，留数定理とかでは residue の略称で使う（residue の和訳に留数も含まれる）こともあるのですが，今は restrict の意味合いで使います

よって， $\displaystyle - \mu^{\ast} = - b + \sum_{j = 1}^n s_j a_j \in \mathbb{Z} / q \mathbb{Z}$ から $- \mu^{\ast \prime} \in \mathbb{Z} / 2 N \mathbb{Z}$ に変換するには， $a_{j, \textrm{res}}, \ b_{\textrm{res}}$ を使って， $\displaystyle - \mu^{\ast}_{\textrm{res}} = - b_{\textrm{res}} + \sum_{j = 1}^n s_j a_{j, \textrm{res}} \in \mathbb{Z} / 2 N \mathbb{Z}$ で実現できます．

よって， $- \mu^{\ast}_{\textrm{res}} \in \mathbb{Z} / 2 N \mathbb{Z}$ ゆえ，test polynomial $\tilde{v}_{\textrm{res}} = v_{0, \textrm{res}} + v_{1, \textrm{res}} X + \cdots + v_{N - 1, \textrm{res}} X^{N - 1} \in \hat{\mathbb{Z}}_N[X]$ は $v_i = \mathrm{Upper}_{q, p}(i)$ に対して， $\displaystyle v_{i, \textrm{res}} = \mathrm{Upper}_{q, p}(\frac{q}{2 N} i)$ とすればOKです．

まとめると， $- \mu^{\ast}$ の定義域は， $\displaystyle - \mu^{\ast} = - b + \sum_{j = 1}^n s_j a_j$ において， $\displaystyle a_{j, \textrm{res}} = \left \lfloor \frac{2 N a_j}{q} \right \rceil, \ b_{\textrm{res}} = \left \lfloor \frac{2 N b}{q} \right \rceil$ として， $\displaystyle - \mu^{\ast}_{\textrm{res}} = - b_{\textrm{res}} + \sum_{j = 1}^n s_j a_{j, \textrm{res}} \in \mathbb{Z} / 2 N \mathbb{Z}$ と修正し，test polynomial $v$ を $\tilde{v}_{\textrm{res}} = v_{0, \textrm{res}} + v_{1, \textrm{res}} X + \cdots + v_{N - 1, \textrm{res}} X^{N - 1} \in \hat{\mathbb{Z}}_N[X], \ v_{i, \textrm{res}} = \mathrm{Upper}_{q, p}(\frac{2 N}{q} i)$ と修正することで， $X^{- \mu^{\ast}_{\textrm{res}}} \cdot \tilde{v}_{\textrm{res}}$ を求めることが目標，とできます．

最後にRescalingのアルゴリズムをまとめておきます．

bootstrapでやりたいこと

上記でやりたかったことは，「暗号文のノイズを取り除く」ことです．ノイズは，下位 $\Omega - (\bar{w} + w) - 1$ bit に格納されているのですから，そこをなるべく0にすればOKです．
そのためには，

$X^{- \mu^{\ast}_{\textrm{res}}} \cdot \tilde{v}_{\textrm{res}}$ を求めることが目標

でした．
では，このことをどのようにして実現すればいいでしょうか．そして，今回の「Rescaling」の3つ目の問題点である「秘密鍵はそのままでいいのか？」についても考察します．

以下では，Blind Rotation, Sample Extraction, Key Switching と3つのアルゴリズムが出てくるのですが，（前の Rescaling もまとめて）それぞれの処理を図示しました．

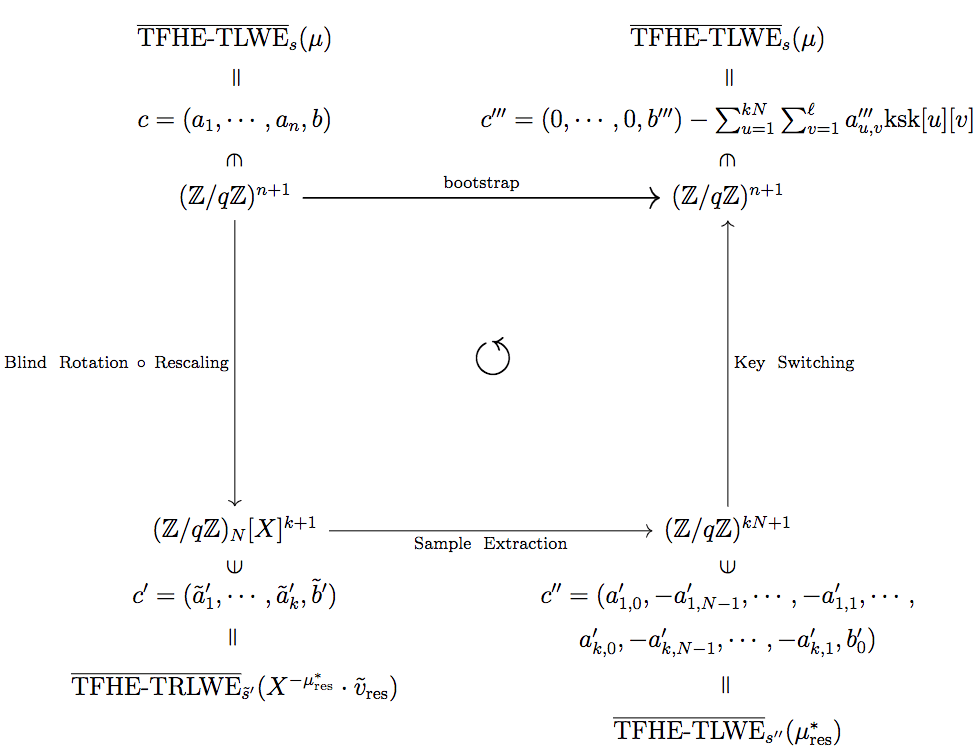
$\textrm{Blind \ Rotation} \ \circ \ \textrm{Rescaling}$ は下記の図で，左上の $(\mathbb{Z} / q \mathbb{Z})^{n + 1}$ から右下の $(\mathbb{Z} / q \mathbb{Z})_N[X]^{k + 1}$ に向かう射のことです．

＊五角形の図式にしようかとも思ったのですが，少し見栄えが悪いので，上記のような形にしました

上記の可換図式を射ごとにざっくり説明します．Rescaling 以外のそれぞれの要素については次章以降で説明します．

Blind Rotation
$\hat{\mathbb{Z}} = \mathbb{Z} / q \mathbb{Z}$ 内での計算で秘密鍵 $\tilde{s}^{\prime}$ のもとで $c = \overline{\textrm{TFHE-TLWE}}_{s}(\mu) \in \hat{\mathbb{Z}}^{n + 1}$ から $c^{\prime} = \overline{\textrm{TFHE-TRLWE}}_{\tilde{s}^{\prime}}(X^{- \tilde{\mu}^{\ast}_{\textrm{res}}} \cdot \tilde{v}^{\prime}) \in \hat{\mathbb{Z}}_N[X]^{k + 1}$ を求める

Sample Extraction
$c^{\prime} = \overline{\textrm{TFHE-TRLWE}}_{\tilde{s}^{\prime}}(X^{- \tilde{\mu}^{\ast}_{\textrm{res}}} \cdot \tilde{v}^{\prime}) \in \hat{\mathbb{Z}}_N[X]^{k + 1}$ から $c^{\prime \prime} = (a^{\prime}_{1, 0}, - a^{\prime}_{1, N - 1}, \cdots, - a^{\prime}_{1, 1}, \cdots, a^{\prime}_{k, 0}, - a^{\prime}_{k, N - 1}, \cdots, - a^{\prime}_{k, 1}, b^{\prime}_0) \in (\mathbb{Z} / q \mathbb{Z})^{kN + 1}$ を求める．

Key Switching
$c^{\prime \prime} = (a^{\prime}_{1, 0}, - a^{\prime}_{1, N - 1}, \cdots, - a^{\prime}_{1, 1}, \cdots, a^{\prime}_{k, 0}, - a^{\prime}_{k, N - 1}, \cdots, - a^{\prime}_{k, 1}, b^{\prime}_0) \in (\mathbb{Z} / q \mathbb{Z})^{kN + 1}$ から秘密鍵 $s$ による $c^{\prime \prime \prime} = (0, \cdots, 0, b^{\prime \prime \prime}) - \sum_{u = 1}^{kN} \sum_{v = 1}^{\ell} a^{\prime \prime \prime}_{u, v} \mathrm{ksk}[u][v] = \overline{\textrm{TFHE-TLWE}}_{s}(\mu) \in \hat{\mathbb{Z}}^{n + 1}$ を求める．

となります．厳密には，Blind Rotation には，Rescaling の操作も含まれています．

つまり， $c = \overline{\textrm{TFHE-TLWE}}_{s}(\mu) \in \hat{\mathbb{Z}}^{n + 1}$ に対して，
Blind Rotation → Sample Extraction → Key Swithing
と処理を施すと， $c^{\prime \prime \prime} = \overline{\textrm{TFHE-TLWE}}_{s}(\mu) \in \hat{\mathbb{Z}}^{n + 1}$ が得られて，これがほしいものでした．

上記の３つのアルゴリズムの input と output が明らかになりました．
では，その過程でやることを軽く解説しようと思います．詳細については，各項目で解説します．

Blind Rotation
秘密鍵云々はここで考えます．具体的には，CMux gate を使う際に，元の秘密鍵を別に秘密鍵 $s^{\prime}$ での $\textrm{GGSW-TRLWE}$ 方式の暗号化でマスキングをします．
更に，External product も考えるため， $\textrm{TFHE-TRLWE}$ 方式の暗号化も登場します．

Sample Extraction
実は，Blind Rotation でやりたいことはほぼできているのですが，問題が２つあります．

Blind Rotation の出力は多項式だが，実際は整数
秘密鍵が変更されたまま

Sample Extraction では前者を考えます．ここで，多項式の係数だけを取り出すことを考えます．
そこで，最終的に定数項のみに関わる部分のみを抜き出すことで，多項式の話から整数に戻します．

Key Switching
Blind Rotation で鍵を変更してから，元の秘密鍵に戻すことを考えます．そのために導出する式はいかついですが，きちんと全て修正されながら戻っていて，その結果初め（全体のinput）にあったノイズも取り除けています．

目的はこのようなものでした．

$\hat{\mathbb{Z}} = \mathbb{Z} / q \mathbb{Z}$ 内での計算で秘密鍵 $\tilde{s}^{\prime}$ のもとで $c = \overline{\textrm{TFHE-TLWE}}_{s}(\mu) \in \hat{\mathbb{Z}}^{n + 1}$ から $c^{\prime} = \overline{\textrm{TFHE-TRLWE}}_{\tilde{s}^{\prime}}(X^{- \tilde{\mu}^{\ast}_{\textrm{res}}} \cdot \tilde{v}^{\prime}) \in \hat{\mathbb{Z}}_N[X]^{k + 1}$ を求める

Rescaling は行なったものとします．やりたいことから順に手順を遡ってみます．実装ということで，少し効率性も考えます．

$X^{- \mu^{\ast}_{\textrm{res}}} \cdot \tilde{v}_{\textrm{res}}$ を求めたい
$\rightarrow$ そのためには， $X^{- \mu^{\ast}_{\textrm{res}}} = X^{- b_{\textrm{res}} + \sum_{i = 1}^n s_i a_{i, \textrm{res}}}$ を求める必要がある
$\rightarrow$ $i - 1$ 番目の $X^{- b_{\textrm{res}} + \sum_{h = 1}^{i - 1} s_h a_{h, \textrm{res}}}$ まで求まっているなら，それに $X^{s_i a_{i, \textrm{res}}}$ を掛ければいいので， $X^{s_i a_{i, \textrm{res}}}$ を求める必要がある（０番目の初期値は $X^{- b_{\textrm{res}}}$ としている）
$\rightarrow$ $X^{s_i \cdot a_{i, \textrm{res}}}$ の部分は， $s_i \in \{0, 1\}$ であり，CMux gate を使える（ $s_i$ の値で場合分けをしなくていい）
$\rightarrow$ 考える必要がある部分は，実質， $X^{- b_{\textrm{res}} + \sum_{h = 1}^{i - 1} s_h a_{h, \textrm{res}}} \cdot X^{a_{i, \textrm{res}}}$ のみ

ここで， $\textrm{CMux}$ の部分を整理してみましょう．

参照：第３回「CMuxゲート」

$\textrm{CMux}$ は，引数を3つ取り，1つめは0か1を $\textrm{GGSW-TRLWE}$ で暗号化したもので，2つめと3つめは $\textrm{TFHE-TRLWE}$ 方式の暗号文でした．
$s_i \in \{0, 1\}$ ですので， $s_i$ を $\textrm{GGSW-TRLWE}$ で暗号化したものを１つ目の引数にすればOKです．そして，そこの暗号化では別の秘密鍵が必要になります．
と同時に，今回の「4.1でやりたいこと」での「秘密鍵はそのままでいいのか？」も $s_i$ を適当な暗号化でマスクしたことになるので，これで解決したことになります．

次に $\textrm{TFHE-TRLWE}$ 方式の暗号文を用意する必要がありますが，これは， $X^{- b_{\textrm{res}} + \sum_{h = 1}^{i - 1} s_h a_{h, \textrm{res}}}$ と $X^{- b_{\textrm{res}} + \sum_{h = 1}^{i - 1} s_h a_{h, \textrm{res}}} \cdot X^{a_{i, \textrm{res}}}$ をそれぞれ $\textrm{TFHE-TRLWE}$ 方式で暗号化したものを用意すればOKです．
これは， $\textrm{CMux}$ の演算で External product が出てくるためです．

参照：第３回「TFHE方式の暗号文とGGSW方式の暗号文の外積」

以上の議論をまとめると，

\begin{align*} \textrm{CMux}(\overline{\textrm{GGSW-TRLWE}}_{\tilde{s}^{\prime}}(s_i), \overline{\textrm{TFHE-TRLWE}}_{\tilde{s}^{\prime}}(X^{- b_{\textrm{res}} + \sum_{h = 1}^{i - 1} s_h a_{h, \textrm{res}}} \cdot \tilde{v}_{\textrm{res}}), \overline{\textrm{TFHE-TRLWE}}_{\tilde{s}^{\prime}}(X^{- b_{\textrm{res}} + \sum_{h = 1}^{i - 1} s_h a_{h, \textrm{res}}} \cdot X^{a_{i, \textrm{res}}} \cdot \tilde{v}_{\textrm{res}})) \end{align*}

このようになります．ここで，新しく出てきた秘密鍵 $\tilde{s}^{\prime}$ は，このときのためだけに使用する鍵で， $\tilde{s}^{\prime} \in \mathbb{B}_N[X]^k$ です．
また，External product では，互いの秘密鍵を合わせる必要があるため， $\textrm{TFHE-TRLWE}$ 方式でも $\tilde{s}^{\prime}$ 　を使う必要があります．

とすると，最終的にでてくるアウトプットは，

\begin{align*} \overline{\textrm{TFHE-TRLWE}}_{\tilde{s}^{\prime}}(X^{- b_{\textrm{res}} + \sum_{i = 1}^{n} s_i a_{i, \textrm{res}}} \cdot \tilde{v}_{\textrm{res}}) \end{align*}

となり， $- \mu^{\ast}_{\textrm{res}} = - b_{\textrm{res}} + \sum_{i = 1}^n s_i a_{i, \textrm{res}}$ でしたから，上記のアウトプットは

\begin{align*} \overline{\textrm{TFHE-TRLWE}}_{\tilde{s}^{\prime}}(X^{- \mu^{\ast}_{\textrm{res}}} \cdot \tilde{v}_{\textrm{res}}) \end{align*}

このようにまとめられます．

最後に Blind Rotation のアルゴリズムをまとめておきます．
以下では， $\textrm{ACC}$ というのを使って（accumulatorの略），途中の

\begin{align*} \overline{\textrm{TFHE-TRLWE}}_{\tilde{s}^{\prime}}(X^{- b_{\textrm{res}} + \sum_{h = 1}^{i - 1} s_h a_{h, \textrm{res}}} \cdot \tilde{v}_{\textrm{res}}) \end{align*}

を表現していますが， $\textrm{ACC}$ だと何に依存するか分かりづらいなって思っています．

Sample Extraction

目的はこのようなものでした．

$c^{\prime} = \overline{\textrm{TFHE-TRLWE}}_{\tilde{s}^{\prime}}(X^{- \tilde{\mu}^{\ast}_{\textrm{res}}} \cdot \tilde{v}^{\prime}) \in \hat{\mathbb{Z}}_N[X]^{k + 1}$ から $c^{\prime \prime} = (a^{\prime}_{1, 0}, - a^{\prime}_{1, N - 1}, \cdots, - a^{\prime}_{1, 1}, \cdots, a^{\prime}_{k, 0}, - a^{\prime}_{k, N - 1}, \cdots, - a^{\prime}_{k, 1}, b^{\prime}_0) \in (\mathbb{Z} / q \mathbb{Z})^{kN + 1}$ を求める．

大雑把には，「TRLWEに出てくる多項式をベクトルと見て，それらを連結させて， $\mathbb{Z} / q \mathbb{Z}$ の１つのベクトルと考えることで，TLWEの暗号文とみなす」というものです．

↓を見れば難しいことはやっていないと分かると思います．

Blind Rotation で出てきた秘密鍵 $\tilde{s}^{\prime} = (\tilde{s}^{\prime}_1, \cdots, \tilde{s}^{\prime}_{N - 1}) \in \mathbb{B}_N[X]^k$ と $1 \leq j \leq k$ に対して， $\tilde{s}^{\prime}_j = s^{\prime}_{j, 0} + s^{\prime}_{j, 1} X + \cdots + s^{\prime}_{j, N - 1} X^{N - 1}$ とします．
また，input である $c^{\prime} = (\tilde{a}^{\prime}_1, \cdots, \tilde{a}^{\prime}_k, \tilde{b}^{\prime})$ と $1 \leq j \leq k$ に対して， $\tilde{a}^{\prime}_j = a^{\prime}_{j, 0} + a^{\prime}_{j, 1} X + \cdots + a^{\prime}_{j, N - 1} X^{N - 1}$ と $\tilde{b}^{\prime} = b^{\prime}_{0} + b^{\prime}_{1} X + \cdots + b^{\prime}_{N - 1} X^{N - 1}$ とします．
このとき，

\begin{align*} c^{\prime \prime} &= (a^{\prime}_{1, 0}, - a^{\prime}_{1, N - 1}, \cdots, - a^{\prime}_{1, 1}, a^{\prime}_{2, 0}, - a^{\prime}_{2, N - 1}, \cdots, - a^{\prime}_{2, 1}, \cdots, a^{\prime}_{k, 0}, - a^{\prime}_{k, N - 1}, \cdots, - a^{\prime}_{k, 1}, b^{\prime}_0) \\ &\in (\mathbb{Z} / q \mathbb{Z})^{k N + 1} \end{align*}

と秘密鍵

\begin{align*} s^{\prime \prime} &= (s^{\prime}_{1, 0}, s^{\prime}_{1, 1}, \cdots, s^{\prime}_{1, N - 1}, s^{\prime}_{2, 0}, s^{\prime}_{2, 1}, \cdots, s^{\prime}_{2, N - 1}, \cdots, s^{\prime}_{k, 0}, s^{\prime}_{k, 1}, \cdots, s^{\prime}_{k, N - 1}) \\ &= (s^{\prime \prime}_1, s^{\prime \prime}_2, \cdots, s^{\prime \prime}_{k N}) \\ &\in \mathbb{B}^{kN} \end{align*}

について

\begin{align*} c^{\prime \prime} = \overline{\textrm{TFHE-TLWE}}_{s^{\prime \prime}}(\mu) \end{align*}

が成り立っています．

上記の証明

input は $c^{\prime} = \overline{\textrm{TFHE-TRLWE}}_{\tilde{s}^{\prime}}(X^{- \tilde{\mu}^{\ast \prime}} \cdot \tilde{v}^{\prime}) = (\tilde{a}_1^{\prime}, \cdots, \tilde{a}_k^{\prime}, \tilde{b}^{\prime})$ なので， $\exists \tilde{e} \in \hat{\mathbb{Z}}_N[X]^k$ を用いて，

\begin{align*} \displaystyle \tilde{b}^{\prime} = \sum_{j = 1}^k \tilde{a}_j^{\prime} \cdot \tilde{s}_j^{\prime} + X^{- \tilde{\mu}^{\ast \prime}} \cdot \tilde{v}^{\prime} + \tilde{e} \end{align*}

が成り立っています．この式の定数項のみに着目します． $\tilde{b}^{\prime} = b^{\prime}_{0} + b^{\prime}_{1} X + \cdots + b^{\prime}_{N - 1} X^{N - 1}$ とすると，左辺の定数項は $b^{\prime}_{0}$ です．
右辺の定数項を考えます． $X^N = - 1$ であることに着目すると，まず， $\sum$ の中の定数項は

\begin{align*} & a^{\prime}_{j, 0} \cdot s^{\prime}_{j, 0} + a^{\prime}_{j, 1} \cdot s^{\prime}_{j, N - 1} \cdot (-1) + \cdots + a^{\prime}_{j, N - 1} \cdot s^{\prime}_{j, 1} \cdot (-1) \\ & = a^{\prime}_{j, 0} \cdot s^{\prime}_{j, 0} + (- a^{\prime}_{j, N - 1}) \cdot s^{\prime}_{j, 1} + \cdots + (- a^{\prime}_{j, 1}) \cdot s^{\prime}_{j, N - 1} \end{align*}

です．次に $X^{- \tilde{\mu}^{\ast \prime}} \cdot \tilde{v}^{\prime}$ の定数項は $\mu$ そのものでした．
最後に $\tilde{e}$ の定数項は $e$ とすると，以上をまとめて，

\begin{align*} \displaystyle b^{\prime}_{0} = \sum_{j = 1}^k a^{\prime}_{j, 0} \cdot s^{\prime}_{j, 0} + (- a^{\prime}_{j, N - 1}) \cdot s^{\prime}_{j, 1} + \cdots + (- a^{\prime}_{j, 1}) \cdot s^{\prime}_{j, N - 1} + \mu + e \end{align*}

を得ます． $(s^{\prime}_{j, 0}, s^{\prime}_{j, 1}, \cdots, s^{\prime}_{j, N - 1})$ を $j = 1$ から $k$ まで並べたベクトルは， $s^{\prime \prime}$ に対応します．
以上から，秘密鍵 $s^{\prime \prime}$ で $\mu$ を暗号化したものが $c^{\prime \prime}$ に対応することが示されました．

最後に Sample Extraction のアルゴリズムをまとめておきます．

Key Switching

目的はこのようなものでした．

$c^{\prime \prime} = (a^{\prime}_{1, 0}, - a^{\prime}_{1, N - 1}, \cdots, - a^{\prime}_{1, 1}, \cdots, a^{\prime}_{k, 0}, - a^{\prime}_{k, N - 1}, \cdots, - a^{\prime}_{k, 1}, b^{\prime}_0) \in (\mathbb{Z} / q \mathbb{Z})^{kN + 1}$ から秘密鍵 $s$ による $c^{\prime \prime \prime} = (0, \cdots, 0, b^{\prime \prime \prime}) - \sum_{u = 1}^{kN} \sum_{v = 1}^{\ell} a^{\prime \prime \prime}_{u, v} \mathrm{ksk}[u][v] = \overline{\textrm{TFHE-TLWE}}_{s}(\mu) \in \hat{\mathbb{Z}}^{n + 1}$ を求める．

Key Switching とは，平文をそのままだけど秘密鍵を変更することで，暗号文を変更する手法のことです．
やりたいこととしては，Blind Rotation で変わってしまった秘密鍵を元に戻します．

以下では，gadget decomposition を使用するため， $\ell$ 桁の $B$ 進展開を行うようにパラメタを予め設定しておきます．
ここで， $\mathrm{ksk}[u][v](1 \leq u \leq kN, \ 1 \leq v \leq \ell)$ という二重配列(key switching key の略)を用意し， $u, v$ を固定したとき， $\mathrm{ksk}[u][v] = \overline{\textrm{TFHE-TLWE}}_{s}(s_u^{\prime \prime} \cdot \frac{q}{B^v})$ という値を格納するものとします．
また，input である $c^{\prime \prime} = (a^{\prime}_{1, 0}, - a^{\prime}_{1, N - 1}, \cdots, - a^{\prime}_{1, 1}, a^{\prime}_{2, 0}, - a^{\prime}_{2, N - 1}, \cdots, - a^{\prime}_{2, 1}, \cdots, a^{\prime}_{k, 0}, - a^{\prime}_{k, N - 1}, \cdots, - a^{\prime}_{k, 1}, b^{\prime}_0)$ について，

\begin{align*} & (a^{\prime}_{1, 0}, - a^{\prime}_{1, N - 1}, \cdots, - a^{\prime}_{1, 1}, a^{\prime}_{2, 0}, - a^{\prime}_{2, N - 1}, \cdots, - a^{\prime}_{2, 1}, \cdots, a^{\prime}_{k, 0}, - a^{\prime}_{k, N - 1}, \cdots, - a^{\prime}_{k, 1}) \\ & = (a^{\prime \prime}_1, \cdots, a^{\prime \prime}_{kN}) \end{align*}

とインデックスを変更して， $b^{\prime}_0$ も $b^{\prime \prime \prime}$ に変更しておきます（３つ $\prime$ 付けたのは誤植ではありません）．
さらに， $1 \leq u \leq kN$ に対して， $a^{\prime \prime}_{u}$ の gadget decomposition を考えて， $g^{-1}(a^{\prime \prime}_{u}) = (a^{\prime \prime \prime}_{u, 1}, a^{\prime \prime \prime}_{u, 2}, \cdots, a^{\prime \prime \prime}_{u, \ell})$ とします．つまり， $\varepsilon < B^{- \ell}$ なる $\varepsilon$ を使って，

\begin{align*} \displaystyle a^{\prime \prime}_{u} = q \sum_{v = 1}^{\ell} a^{\prime \prime \prime}_{u, v} B^{- v} + \varepsilon \end{align*}

が成り立っています．

更に， $c^{\prime \prime \prime} \in (\mathbb{Z} / q \mathbb{Z})^{n + 1}$ を

\begin{align*} \displaystyle c^{\prime \prime \prime} = (0, \cdots, 0, b^{\prime \prime \prime}) - \sum_{u = 1}^{kN} \sum_{v = 1}^{\ell} a^{\prime \prime \prime}_{u, v} \mathrm{ksk}[u][v] \hspace{10pt} \cdots \ (\star) \end{align*}

と置くと， $c^{\prime \prime \prime}$ は秘密鍵 $s$ のもとで， $\mu$ を暗号化したものになっています．

上記の証明

まず， $c^{\prime \prime \prime}$ を考えるには， $(0, \cdots, 0, b^{\prime \prime \prime})$ と $\displaystyle \sum_{u = 1}^{kN} \sum_{v = 1}^{\ell} a^{\prime \prime \prime}_{u, v} \mathrm{ksk}[u][v]$ のベクトルの引き算が定義される必要がありますが，
後者が $(n + 1)$ 次元ベクトルとはパッと見だと分からないので，まずはここを考えます．

$\textrm{TFHE-TLWE}$ 方式の暗号文では，足し算とスカラー倍が定義されている（足し算とスカラー倍で閉じている）ことを思い出しましょう．

\begin{align*} \displaystyle & \sum_{u = 1}^{kN} \sum_{v = 1}^{\ell} a^{\prime \prime \prime}_{u, v} \mathrm{ksk}[u][v] \\ & = \sum_{u = 1}^{kN} \sum_{v = 1}^{\ell} a^{\prime \prime \prime}_{u, v} \overline{\textrm{TFHE-TLWE}}_{s}(s_u^{\prime \prime} \cdot \frac{q}{B^v}) \\ & = \sum_{u = 1}^{kN} \sum_{v = 1}^{\ell} \overline{\textrm{TFHE-TLWE}}_{s}(s_u^{\prime \prime} \cdot q \cdot a^{\prime \prime \prime}_{u, v} \cdot B^{- v}) \\ & = \sum_{u = 1}^{kN} (\overline{\textrm{TFHE-TLWE}}_{s}(s_u^{\prime \prime} \cdot q \cdot a^{\prime \prime \prime}_{u, 1} \cdot B^{- 1}) + \overline{\textrm{TFHE-TLWE}}_{s}(s_u^{\prime \prime} \cdot q \cdot a^{\prime \prime \prime}_{u, 2} \cdot B^{- 2}) + \cdots + \overline{\textrm{TFHE-TLWE}}_{s}(s_u^{\prime \prime} \cdot q \cdot a^{\prime \prime \prime}_{u, \ell} \cdot B^{- \ell})) \\ & = \sum_{u = 1}^{kN} (\overline{\textrm{TFHE-TLWE}}_{s}(s_u^{\prime \prime} \cdot q \cdot (a^{\prime \prime \prime}_{u, 1} \cdot B^{- 1} + a^{\prime \prime \prime}_{u, 2} \cdot B^{- 2} + \cdots + a^{\prime \prime \prime}_{u, \ell} \cdot B^{- \ell})) \\ & = \sum_{u = 1}^{kN} (\overline{\textrm{TFHE-TLWE}}_{s}(s_u^{\prime \prime} \cdot q \cdot \sum_{v = 1}^{\ell} a^{\prime \prime \prime}_{u, v} \cdot B^{- v} ) \\ & = \sum_{u = 1}^{kN} \overline{\textrm{TFHE-TLWE}}_{s}(s_u^{\prime \prime} \cdot a^{\prime \prime}_u) \\ & = \overline{\textrm{TFHE-TLWE}}_{s}(s_1^{\prime \prime} \cdot a^{\prime \prime}_1) + \overline{\textrm{TFHE-TLWE}}_{s}(s_2^{\prime \prime} \cdot a^{\prime \prime}_2) + \cdots + \overline{\textrm{TFHE-TLWE}}_{s}(s_{kN}^{\prime \prime} \cdot a^{\prime \prime}_{kN}) \\ & = \overline{\textrm{TFHE-TLWE}}_{s}(\sum_{u = 1}^{kN} s_u^{\prime \prime} \cdot a^{\prime \prime}_u) \\ & = (a_1, \cdots, a_n, \sum_{i = 1}^{n} a_i \cdot s_i + \sum_{u = 1}^{kN} s^{\prime \prime}_u \cdot a^{\prime \prime}_u + e^{\prime \prime}) \end{align*}

それぞれの行の式変形の根拠を下記にまとめておきます：
2. $\mathrm{ksk}[u][v]$ の定義
3. $\textrm{TFHE-TLWE}$ 方式の暗号文でのスカラー倍
4. $\displaystyle \sum_{v = 1}^{\ell}$ を展開
5. $\textrm{TFHE-TLWE}$ 方式の暗号文での足し算
6. $\displaystyle \sum_{v = 1}^{\ell}$ でまとめる
7. $a_u^{\prime \prime}$ の gadget decomposition の定義
8. $\displaystyle \sum_{u = 1}^{kN}$ を展開
9. $\textrm{TFHE-TLWE}$ 方式の暗号文での足し算
10. $\textrm{TFHE-TLWE}$ 方式の暗号文の定義

以上より， $\displaystyle \sum_{u = 1}^{kN} \sum_{v = 1}^{\ell} a^{\prime \prime \prime}_{u, v} \mathrm{ksk}[u][v]$ が長さ $n + 1$ のベクトルであることが分かりました．
さて，

\begin{align*} \displaystyle b^{\prime}_{0} = \sum_{j = 1}^k a^{\prime}_{j, 0} \cdot s^{\prime}_{j, 0} + (- a^{\prime}_{j, N - 1}) \cdot s^{\prime}_{j, 1} + \cdots + (- a^{\prime}_{j, 1}) \cdot s^{\prime}_{j, N - 1} + \mu + e \end{align*}

でしたから，インデックスを整理すると，

\begin{align*} \displaystyle b^{\prime \prime} = \sum_{u = 1}^{kN} a^{\prime \prime}_{u} \cdot s^{\prime \prime}_{u} + \mu + e \end{align*}

です．よって，

\begin{align*} \displaystyle c^{\prime \prime \prime} &= (0, \cdots, 0, b^{\prime \prime \prime}) - \sum_{u = 1}^{kN} \sum_{v = 1}^{\ell} a^{\prime \prime \prime}_{u, v} \mathrm{ksk}[u][v] \\ &= (0, \cdots, 0, b^{\prime \prime \prime}) - (a_1, \cdots, a_n, \sum_{i = 1}^{n} a_i \cdot s_i + \sum_{u = 1}^{kN} s_u^{\prime \prime} \cdot a^{\prime \prime}_u + e^{\prime \prime}) \\ &= (- a_1, \cdots, - a_n, b^{\prime \prime \prime} - \sum_{i = 1}^{n} a_i \cdot s_i - \sum_{u = 1}^{kN} s^{\prime \prime}_u \cdot a^{\prime \prime}_u - e^{\prime \prime}) \\ &= (- a_1, \cdots, - a_n, - \sum_{i = 1}^{n} a_i \cdot s_i + \mu + e^{\prime \prime \prime}) \end{align*}

となります．つまり， $\displaystyle c = (a_1, \cdots, a_n, \sum_{i = 1}^n a_i s_i + \mu + e)$ でのランダムベクトル $(a_1, \cdots, a_n)$ の全ての要素の符号を逆転した $\displaystyle c^{\prime \prime \prime} = (- a_1, \cdots, - a_n, \sum_{i = 1}^n (- a_i) s_i + \mu + e)$ も $\mu$ の暗号文と見ることができます．

以上より示されました．

また，最終的に重要な $(\star)$ については，一見するとどこからその変形が出てくるのか分からない式ですが，次のように考えることで自然と導かれます．

式の導出

本質的に重要な部分は，上の折りたたみ部分の $\overline{\textrm{TFHE-TLWE}}_{s}(\sum_{u = 1}^{kN} s_u^{\prime \prime} \cdot a^{\prime \prime}_u)$ ですので，ここまで考え方を導出します．

最終的にやりたいことは， $\mu$ を $s^{\prime \prime}$ で暗号化したものから $s$ で暗号化したものへ取り替えることです．
つまり， $c^{\prime \prime \prime}$ は，ランダムベクトル $(a_1, \cdots, a_n)$ と秘密鍵 $s$ を使って $\mu$ を暗号化することで構成されます．

よって考えるべきことはランダムベクトル $(a_1, \cdots, a_n)$ と秘密鍵 $s$ をどのようにして作り出すか，ということです．
それには， $\overline{\textrm{TFHE-TLWE}}_s()$ の暗号化を使うのが一番早いことになります．

そして，上記の暗号化に対して， $\mu$ を引数にとるようにすればいいのですが，ここで input を見返してみましょう．
inputでは，

\begin{align*} b^{\prime \prime \prime} = \sum_{u = 1}^{kN} s_u^{\prime \prime} a_u^{\prime \prime} + \mu + e^{\prime \prime} \end{align*}

が成り立っているのでした．つまり，ここから，

\begin{align*} \mu = b^{\prime \prime \prime} - \sum_{u = 1}^{kN} s_u^{\prime \prime} a_u^{\prime \prime} + e^{\prime \prime} \end{align*}

とすることで， $\mu$ の情報を引き出せます．つまり，

\begin{align*} \overline{\textrm{TFHE-TLWE}}_s(\mu) &= \overline{\textrm{TFHE-TLWE}}_s(b^{\prime \prime \prime} - \sum_{u = 1}^{kN} s_u^{\prime \prime} a_u^{\prime \prime} + e^{\prime \prime}) \\ &= \overline{\textrm{TFHE-TLWE}}_s(b^{\prime \prime \prime}) - \overline{\textrm{TFHE-TLWE}}_s(\sum_{u = 1}^{kN} s_u^{\prime \prime} a_u^{\prime \prime}) + \overline{\textrm{TFHE-TLWE}}_s(e^{\prime \prime}) \\ \end{align*}

が成り立ちます．しかし，エラーベクトル部分 $\overline{\textrm{TFHE-TLWE}}_s(e^{\prime \prime})$ が非常に扱いづらいので，どうにかして， $\overline{\textrm{TFHE-TLWE}}_s(b^{\prime \prime \prime}) - \overline{\textrm{TFHE-TLWE}}_s(\sum_{u = 1}^{kN} s_u^{\prime \prime} a_u^{\prime \prime})$ のみにしたいわけです．
ただ，このままだと $\overline{\textrm{TFHE-TLWE}}_s(\cdot)$ のランダムベクトル $(a_1, \cdots, a_n)$ 分が打ち消しあってしまいます．よって， $(0, \cdots, 0, b^{\prime \prime \prime}) - \overline{\textrm{TFHE-TLWE}}_s(\sum_{u = 1}^{kN} s_u^{\prime \prime} a_u^{\prime \prime})$ としてランダムベクトルを打ち消さないようにしているわけです．

以上より，

\begin{align*} c^{\prime \prime \prime} = (0, \cdots, 0, b^{\prime \prime \prime}) - \overline{\textrm{TFHE-TLWE}}_s(\sum_{u = 1}^{kN} s_u^{\prime \prime} a_u^{\prime \prime}) \end{align*}

と考えることができます．

個人的に思うこと

正直，個人的にはここで止めて，別にわざわざ $\mathrm{ksk}[u][v]$ までやらなくてもいいんじゃないかなと思っていて，それは，上記もそうですが，

\begin{align*} c^{\prime \prime \prime} = \overline{\textrm{TFHE-TLWE}}_s(b^{\prime \prime \prime}) - (0, \cdots, 0, \sum_{u = 1}^{kN} s_u^{\prime \prime} a_u^{\prime \prime}) \end{align*}

でも同じ結果を導けます（ランダムベクトルを打ち消す部分で，前を消すか後ろを消すかの違い）し，こっちの方が計算量が少ない気がするからです．

最後に Key Switching のアルゴリズムをまとめておきます．

bootstrapのまとめ

この項目を持って，4.1を振り返りします．まず，bootstrap では，いくつかのアルゴリズムを組合せて，暗号文のノイズを取り除くことが目的でした．

先に図式とアルゴリズムを全て再掲します．

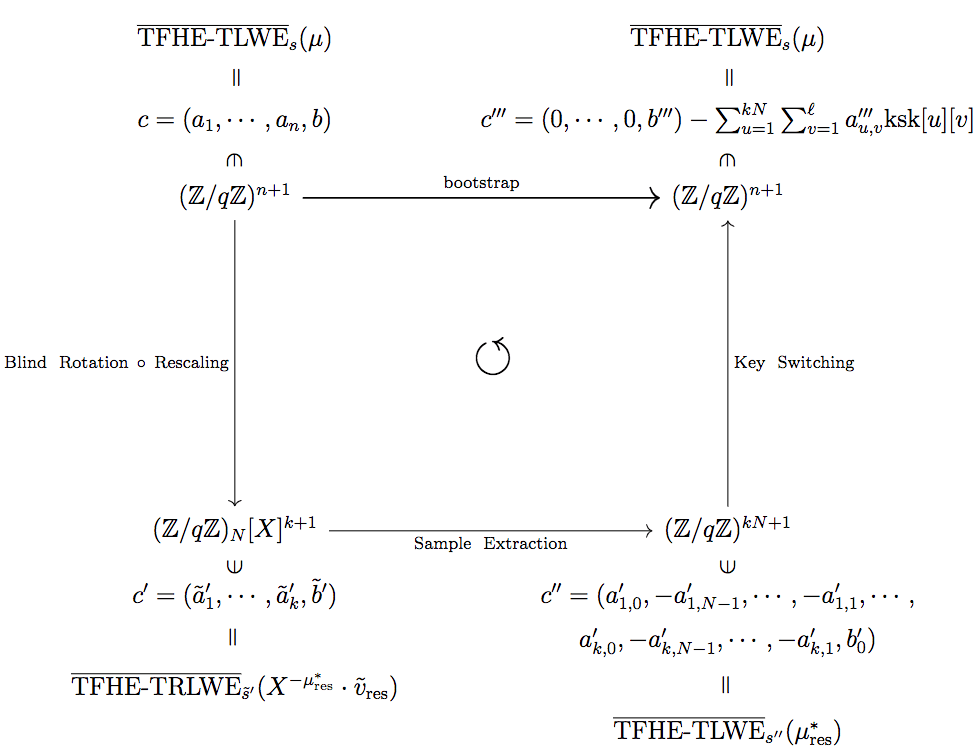
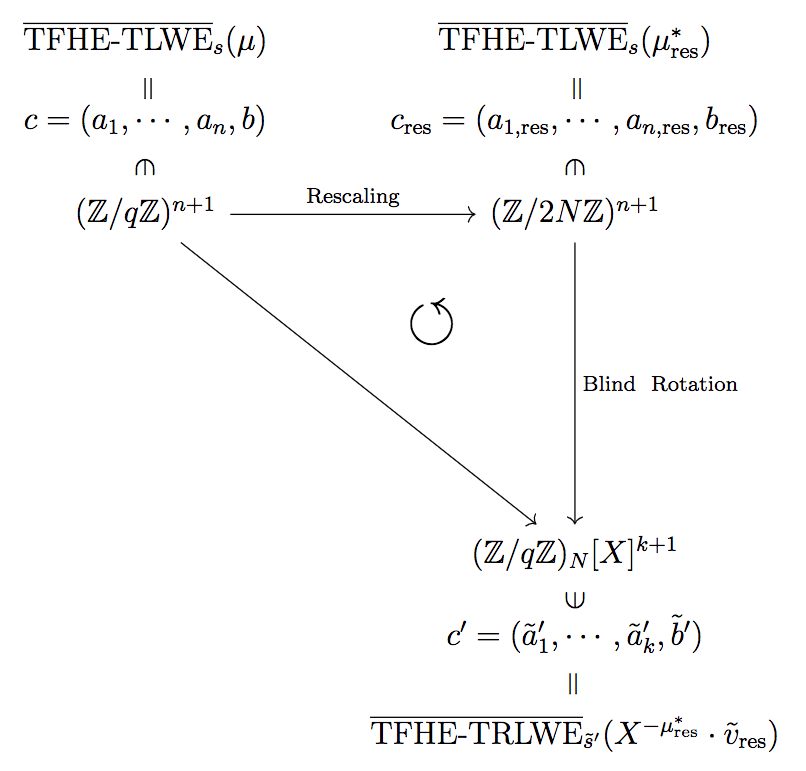
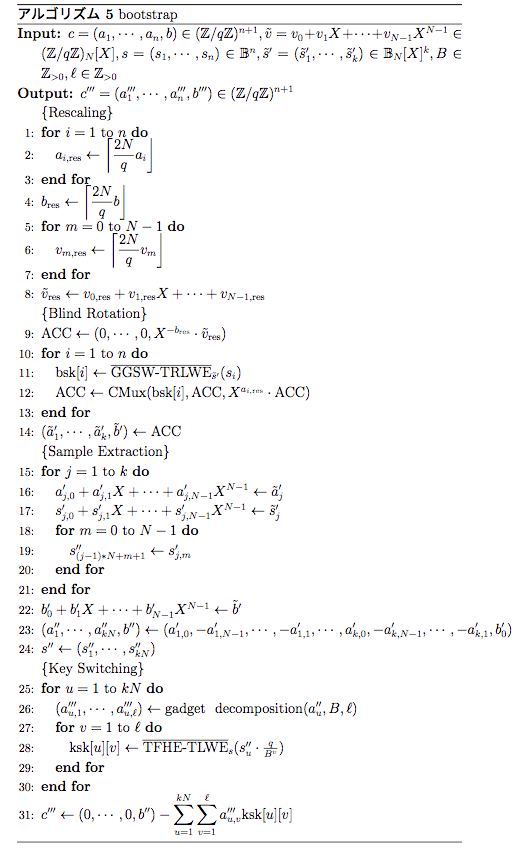
１つずつの細かい説明は，各章を確認してください．

主な流れとしては，Blind Rotation でノイズを取り除く作業を行なったものの，出力結果が多項式になっていることと秘密鍵が変更されていることを解消するために，それぞれ更に，Sample Extraction と Key Switching という関数が必要なのでした．

4.1の議論の考察

ここでは本文の議論をもう１歩踏み込んだ考察をします．踏み込み方は人それぞれだと思うので，興味のない方は飛ばしてくださって構いません．

まず，上記では TFHE-TLWE 方式での bootstrap しか扱いませんでしたが，TFHE-TRLWE 方式でも同様に bootstrap を扱えます．
それは，各係数ごとに test polynomial を作用させればいいからです．

そして，各アルゴリズムをわざわざ擬似コードで書いたのは理由があって，それぞれの計算量のオーダーも見積もってみます．
パラメタは全て今までと同じと仮定します． $q = 2^{\Omega}$ ゆえ， $(a_1, \cdots, a_n) \in (\mathbb{Z} / q \mathbb{Z})^n$ は全て $\Omega$ bit 長であることに注意してください．

まず， $\overline{\textrm{TFHE-TRLWE}}$ と $\overline{\textrm{GGSW-TRLWE}}$ の Encryption については，それぞれ， $O(k N \Omega)$ と $O(k^2 N \ell \Omega)$ です．
また，（引数が多項式のベクトルの）gadget decomposition については， $O(k N \ell \Omega)$ です．
更に， $\textrm{CMux}$ では，External product と $\overline{\textrm{TFHE-TRLWE}}$ の暗号文の和を行なっているので，その計算量は $O(k^2 N \ell^2 \Omega)$ になります．

＊覚えていたら，該当箇所に追記をして，ここにリンクを貼っておきます

では，Rescaling, Blind Rotation, Sample Extraction, Key Switching の４つのオーダーを考えます．
Rescaling
$i$ と $m$ についてループを回し，それぞれ， $a_i, b, v_m$ に関する演算しか行なっていませんので，ここでの計算量は $O(\Omega n) + O(\Omega N)$ です．つまり, $O(\mathrm{max}\{ n, N\} \Omega)$ です．

Blind Rotation
$i$ に関するループを回し，その中では， $\overline{\textrm{GGSW-TRLWE}}$ と $\textrm{CMux}$ の演算のみ行なっています．それぞれの計算量は， $O(k^2 N \ell \Omega)$ と $O(k^2 N \ell^2 \Omega)$ でしたから，トータルの計算量は $O(n k^2 N \ell^2 \Omega)$ です．

Sample Extraction
$k$ に関するループの中で $m$ に関するループを回していますので，計算量は $O(k N \Omega)$ です（データ構造とか並列化とか工夫すればここはめちゃくちゃ早くなりそう）．

Key Switching
$u$ に関するループで gadget decomposition を行なって，更にそのループ中で $v$ に関して， $\overline{\textrm{TFHE-TLWE}}$ 方式の暗号化を行なっていて，それぞれの計算量は $O(k^2 N^2 \ell \Omega)$ と $O(k^2 N \ell \Omega)$ でしたので，トータルの計算量は $O(k^2 N^2 \ell \Omega)$ です．

以上をまとめると，bootstrap 全体での計算量で一番効いているのは Blind Rotation の $O(n k^2 N \ell^2 \Omega)$ です． $\textrm{CMux}$ がめちゃくちゃかかるっていう印象です．

すると，上記の計算量を抑えようとすると， $k$ は秘密鍵 $s^{\prime}$ の鍵長で， $\ell$ は gadget decomposition での桁数指定でしたから，これらをどれだけ抑えられるか，という話になってくると思います．

後，気になっていることとしては，Sample Extraction, Key Exchange の作用させる順番は変更することができるのだろうか，ということです．
もちろん構成自体は変更することになると思いますが，多項式の状態で秘密鍵をもとに戻した後で整数に戻すっていうのもできなくはなさそうだなって思っています．

4.2の議論

4.2では Look-up Table というものが新しく出てくるのですが，大したことはやっていないので，いきなり議論に入ろうと思います．

定義域が $\tilde{D}$ で値域が $\tilde{I}$ なる任意の関数 $f$ を取ります．これは任意の演算を表すものとイメージしてください．
$f$ という任意の演算が暗号文の状態でも実現できるようにするには，次のように考えます．
$\mathrm{Encode} : \tilde{D} \rightarrow \mathbb{Z} / q \mathbb{Z}$ と $\mathrm{Encode}^{\prime} : \tilde{I} \rightarrow \mathbb{Z} / q \mathbb{Z}$ なる関数を取ります．これは cleartext から plaintext への encode を表しています．
そして，それらの逆操作として， $\mathrm{Decode} : \mathbb{Z} / q \mathbb{Z} \rightarrow \tilde{D}$ と $\mathrm{Decode}^{\prime} : \mathbb{Z} / q \mathbb{Z} \rightarrow \tilde{I}$ なる関数が取れます．これは plaintext から cleartext への decode を表しています．

ここで，修正版の test polynomial $\tilde{v} = v_0 + v_1 X + \cdots + v_{N - 1} X^{N - 1}$ で $v_i = \mathrm{Upper}_{q, p}(\frac{q}{2N}i)$ を取ります．

$v_i$ に対して，下記の可換図式を作用させて， $\textrm{Encode}^{\prime} \circ f \circ \textrm{Decode}(v_i) = T[i]$ とします．

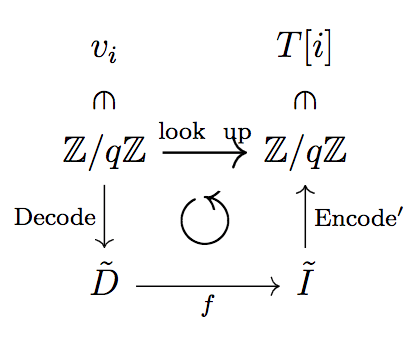
＊上では look up という関数を考えていますが，特に深い意味はなく，筆者が適当に名前をつけただけなので気にしないでください

つまり，今まで，test polynomial の $\mu^{\ast}_{\textrm{res}}$ 番目は $v_i = \mathrm{Upper}_{q, p}(\frac{q}{2N}i)$ で値が固定だったのが， $f$ は任意だったので， $T[i]$ は $\mathbb{Z} / q \mathbb{Z}$ の任意の値をとることができるようになります．

後は，任意の関数 $f$ を作用させた上記の test polynomial と 4.1 での bootstrap を組合せることで，暗号文に任意の関数を作用させた状態で bootstrap つまり暗号文のノイズを取り除けることができるようになりました．

4.2の議論の考察

ここでは本文の議論をもう１歩踏み込んだ考察をします．踏み込み方は人それぞれだと思うので，興味のない方は飛ばしてくださって構いません．

そこまで書くことはないので，上記の注意点を書くことにします．

任意の関数と書いていますが，厳密には全く任意性はありません．それは，Encode をする際に plaintext は $w$ bit までしか格納できないからです．

参照：第２回「3.1の議論」

よって，例えば，上記の図で， $\tilde{D} = \mathbb{Z}, \ \tilde{I} = \mathbb{Q}$ で $f = w^d \ (d \in \tilde{D})$ として， $\mathrm{Decode}$ の移り先が2だった場合， $w^2$ を $\mathrm{Encode}^{\prime}$ することになりますが，これはどうするのか，という問題があります．

以上を考えると，おそらく $f(d)$ を $\mathrm{Encode}^{\prime}$ するのではなく， $f(d) \ \mathrm{mod} \ w$ を $\mathrm{Encode}^{\prime}$ する，と考えるのが妥当でしょう．
すると，任意の関数，ではなく，「移り先を $\mathrm{mod} \ w$ で制限できる任意の関数」と書くのが正確だと思います．

重要な部分は，今回の「4.2の議論」でも書きましたが，

$v_i = \mathrm{Upper}_{q, p}(\frac{q}{2N}i)$ で値が固定だったのが， $f$ は任意だったので， $T[i]$ は $\mathbb{Z} / q \mathbb{Z}$ の任意の値をとることができるようになります．

ここです．値が固定だったものに任意性が入るのは確かに嬉しいですね．

今回の内容はここまでです．ここまでご覧になってくださった方々ありがとうございます！
次回にこれまでのまとめ記事を出します．

全４回通しでの目次

４章の流れ

4.1でやりたいこと

Rescaling

bootstrapでやりたいこと

Blind Rotation

Sample Extraction

Key Switching

bootstrapのまとめ

4.1の議論の考察

4.2の議論

4.2の議論の考察

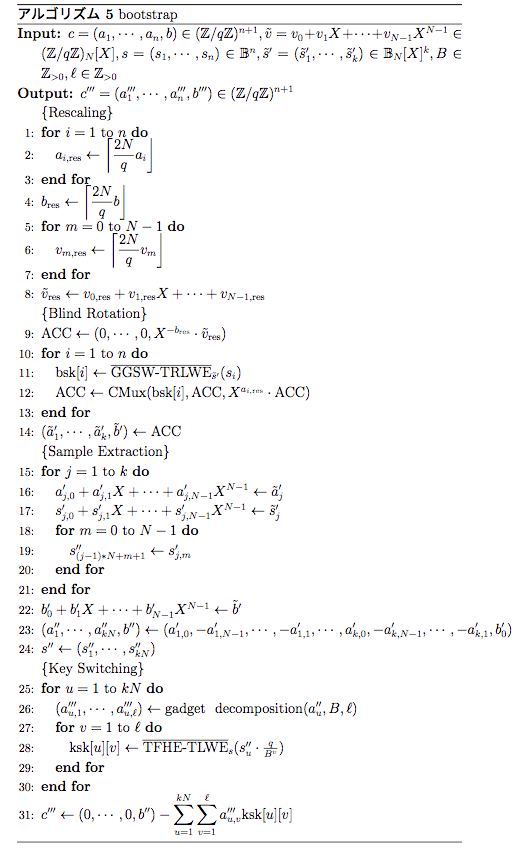
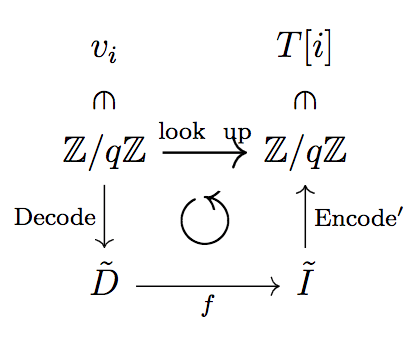
Discussion