具体例で理解するベイズ更新

概要

『ウェブ最適化ではじめる機械学習』なる書籍を読み始めたが、難しくて第一章でつまずいてしまった。数時間考えてようやく曖昧に理解できた気がするので、現時点での自分なりの理解をざっくりと残す。
https://amzn.asia/d/4DmHmxu

ベイズ更新とは

$$P(\theta \mid D) = \frac{P(D \mid \theta) \cdot P(\theta)}{P(D)}$$

という計算式に従って、事後分布を繰り返し更新することで、有用な確率分布を得る手法のこと。
ここで、$\theta$は推論したい未知のパラメータに相当する確率変数を、$D$は実際に観測されたデータを表す。

具体例を使って考える

上記の数式だけではいまいちイメージがつかない方も多いと思うので、具体例を見ながらこの数式の意味を理解してみる。

問題設定

無作為に抽出した対象者に対して

1. ある感染症の検査をおこない、1回陽性という結果が出た場合の感染確率を計算する。
2. ある感染症の検査をおこない、2回陽性という結果が出た場合の感染確率を計算する。

注意点

具体例の中で出てくるデータはすべて適当に設定したものである。
また、今回の具体例では無作為に検査の対象者を抽出することを想定しているが、実際の社会では「周りの人が感染した」とか「初期症状が出ている」といった理由で検査を受けにいく人が大半なので、今回の具体例を現実に素直に適応することは難しい。

事前に分かっているデータ

1. 世界中でこの感染症に感染している人は10%、感染していない人は90%いる。
2. 感染している人の中で、陽性反応が出る人は70%、陰性反応が出る人は30%いる。
3. 感染していない人の中で、陽性反応が出る人は1%、陰性反応が出る人は99%いる。

手順

1. 感染の有無が確定しているときの条件付き確率を表にまとめる

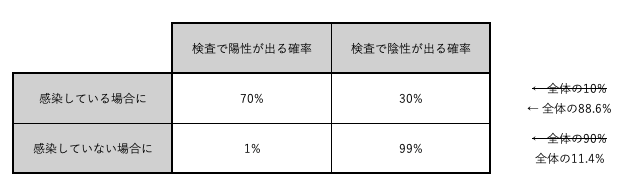
上記の事前に分かっているデータを表にまとめる。
完成した表は以下の画像のようになる。

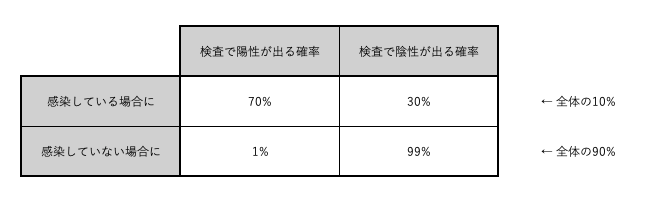
2. 検査の結果が確定しているときの条件付き確率を表にまとめる

手順1で作成した表は、感染の有無が確定しているときの検査の結果の条件付き確率を示しているが、実際の世界では検査の結果が分かっているときの感染の有無の条件付き確率の方が有用なことが多い。
そこで、手順1の表の行と列を入れ替えて、検査の結果が確定しているときの条件付き確率を表にまとめる。

2.1. 条件付き確率を同時確率に変換する

前準備として、手順1でまとめたそれぞれの条件付き確率を同時確率に変換する。
例えば「感染している場合に検査で陽性が出る条件付き確率」に「感染している確率」をかけることで、「感染している、かつ、検査で陽性が出る同時確率」を求めることができる。

手順1の表によると、「感染している場合に検査で陽性が出る条件付き確率」は70%、「感染している人の割合」は10%である。
何も情報がない状態では「感染している人の割合」と「対象者の感染している確率」は同じであると考えて良いので、「対象者の感染している確率」も10%である。
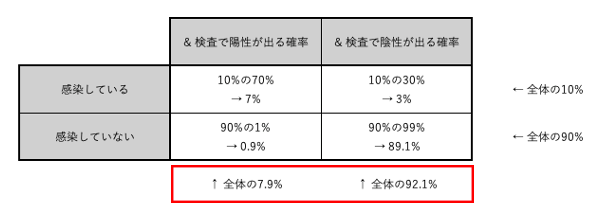
したがって、「感染している、かつ、検査で陽性が出る同時確率」は70% × 10% = 7%となる。
同様の処理を他の3つの条件付き確率に対してもおこなうと、下の画像のようになる。

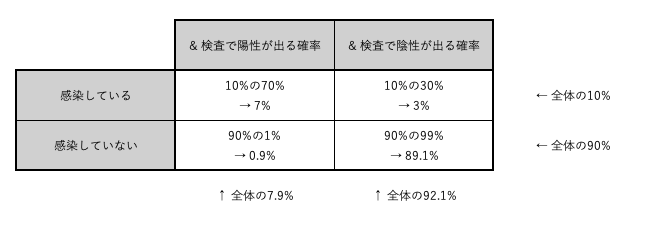
2.2. 行と列を入れ替えて、検査の結果が確定しているときの確率を求める

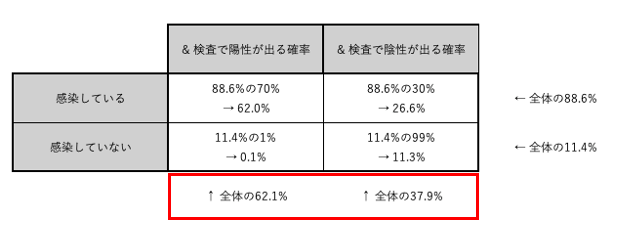
例えば、「検査で陽性が出る確率」は7 + 0.9 = 7.9%、「検査で陽性が出る、かつ、感染している確率」は7%なので、「検査で陽性が出た場合に感染している確率」は7 ÷ 7.9 = 0.8860...で約88.6%となる。
同様の処理を他の3つの同時確率に対してもおこなうと、下の画像のようになる。

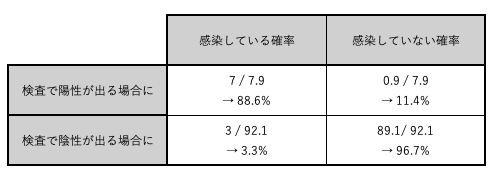
3. 検査結果と手順2.2.の表から現在の感染の確率を求める

もし1回目の検査で陽性が出た場合、手順2.2で作成した表から、感染している確率は88.6%、感染していない確率は11.4%であることがわかる。

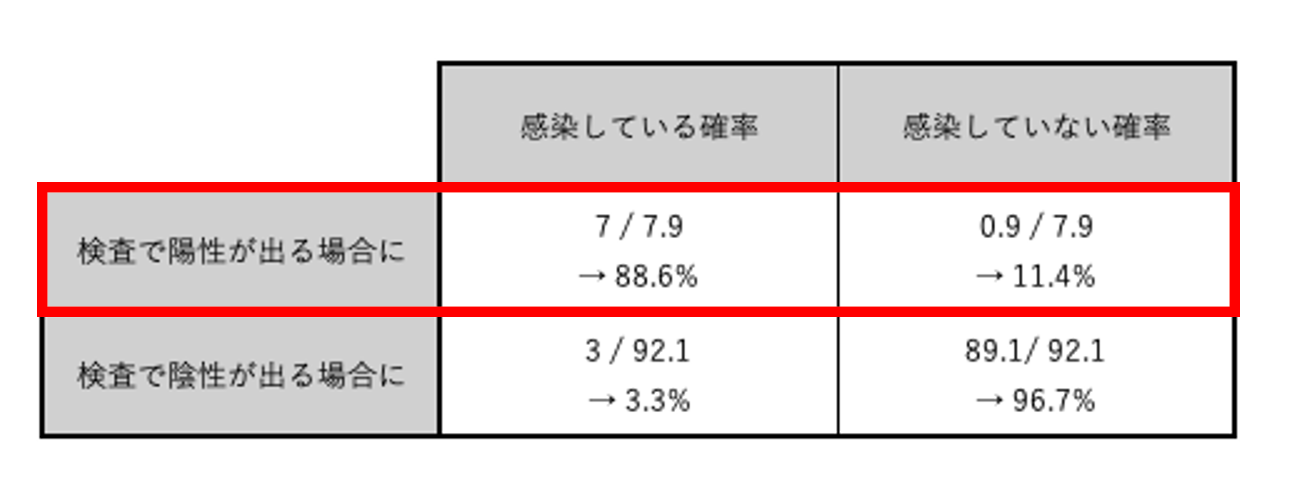
検査結果を見る前の対象者の感染確率は10%であったが、陽性という検査結果が1度出たことで、感染している確率は88.6%へと跳ね上がった。

4. 手順1~3を繰り返す（ただし、最初の感染確率は変更する）

次に、2回目の検査で陽性という結果が出た場合の感染確率を求める。
基本的には手順1 ~ 3の処理を再度繰り返せばよい。ただし、手順1で使用した対象者の感染確率は手順3で求めた感染確率に置き換える。

つまり、これが

こうなって(最初の感染確率を変更して)

こうなって（同時確率を求めて）

こうなる（行と列を入れ替えて条件付き確率を求める）。

つまり2回陽性という検査結果が出た場合、感染している確率は99.8%となる。

5. 結果をまとめる

検査結果	感染している確率
検査0回目	10%
検査1回目(陽性)	88.6%
検査2回目(陽性)	99.8%

具体例と計算式の各項の対応を確認する

$$P(\theta \mid D) = \frac{P(D \mid \theta) \cdot P(\theta)}{P(D)}$$

という計算式の各項が具体例のどのデータと対応するかを確認する。

$P(D \mid \theta)$

$P(D \mid \theta)$を自然言語に直すと、「$\theta$が分かっているときの$D$の確率分布」となる。
$\theta$は未知のパラメータを指すので、今回の場合は対象者の感染の有無に対応する。
$D$は観測されたデータを指すので、今回の場合は検査の結果に対応する。
つまり$P(D \mid \theta)$は「感染の有無が確定しているときの検査結果の確率分布」であり、手順1で使用した下の画像に対応すると考えれば良い。

例えば$P(D=陽性 \mid \theta=感染している) = 70\%$で、$P(D=陰性 \mid \theta=感染していない) = 99\%$となる。

$P(\theta)$

$P(\theta)$を自然言語に直すと、「$\theta$の確率分布」となる。つまり「感染の有無の確率分布」である。
これは手順1や手順4で使用した下の画像に対応する。

$P(\theta)$は検査するごとに変化する確率である。
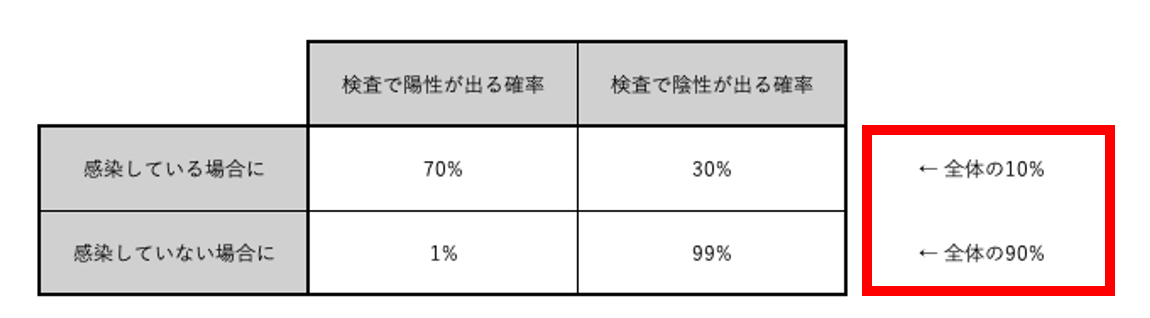
例えば、初期の$P(\theta=感染している)=10\%$で、
1回ベイズ更新をした後の$P(\theta=感染している)=88.6\%$となる。

$P(D)$

$P(D)$を自然言語に直すと、「$D$の確率分布」となる。つまり「検査結果の確率分布」である。
これは手順2や手順4で使用した下の画像に対応する。

$P(D)$も検査するごとに変化する確率である。
例えば、初期の$P(D=陽性)=7.9\%$で、
1回ベイズ更新をした後の$P(D=陽性)=62.1\%$となる。

もう一度数式に戻る

具体例を用いて、計算式の各項が何を指しているかを確認したので、もう一度計算式に戻って、「ある感染症の検査をおこない、1回陽性という結果が出た場合の感染確率」を計算してみる。

「ある感染症の検査をおこない、1回陽性という結果が出た場合の感染確率」は$P(\theta=感染 \mid D=陽性)$であり、ベイズ更新の式より、

$$P(\theta=感染 \mid D=陽性)=\frac{P(D=陽性 \mid \theta=感染) \cdot P(\theta=感染)}{P(D=陽性)}$$

となる。

事前に分かっているデータより

$$P(D=陽性 \mid \theta=感染)=0.7 \\ P(\theta=感染)=0.1$$

である。

また$P(D)$はベイズの定理を使って

$$\begin{aligned} P(D=陽性) &= P(D=陽性 \cap \theta=感染している) + P(D=陽性 \cap \theta=感染していない) \\ &= P(D=陽性 \mid \theta=感染) \cdot P(\theta=感染) + P(D=陽性 \mid \theta=感染していない) \cdot P(\theta=感染していない) \\ &= 0.7 \cdot 0.1 + 0.01 \cdot 0.9 \\ &= 0.079 \end{aligned}$$

である。
これらの結果を上のベイズ更新の式に代入して、

$$P(\theta=感染 \mid D=陽性)=\frac{0.7*0.1}{0.079}=0.886%$$

つまり、1回陽性という結果が出た場合の感染確率が88.6%であるということが計算式のみから導かれた。

まとめ

数式から具体例に行ってまた数式に戻ると理解しやすい。

参考

https://www.youtube.com/watch?v=6MAu12ask3Q

追記(2024-03-05)

もう一つ記事を書きました。
https://zenn.dev/zurukumo/articles/5a6e9182f1ebba