3ポイントシュートの上手さとフリースローの上手さは関係があるか?
概要
『3ポイントシュートの上手さとフリースローの上手さは比例する。』
バスケットボールのファンコミュニティの間では上記のような言説がしばしば常識のように語られる。特に3ポイントシュートが下手な若手の選手に対して、「この選手はフリースローの確率が良いから、そのうち3ポイントの確率も上がっていくはずだ」のような文脈で語られることが多い印象だ。
3ポイントシュートもフリースローもシュートという大枠で見れば同じだが、足を接地した状態で放つフリースローとジャンプと同時に放たれる3ポイントシュートとで本当に上手さは比例するのだろうか?
今回、nba.comのデータを分析して仮説を検証する。
使用するデータ
上記のNBAが公式で提供している2022-23シーズンのデータを使用する。
APIを直接叩くことも可能だが、あまりお行儀が良くない気がするので、今回はChrome Developer Toolsからデータを取得する方法を紹介する。
まずは上記のURLにアクセスし、Chrome Developer Toolsを開く。
次にネットワークタブを開き、検索フィルタに「leaguedashplayerstats」と入力する。
すると「leaguedashplayerstats?College=&Conference=&....」のような名前のJSONデータが1件だけ表示される。もし、該当のデータが表示されない場合はChrome Developer Toolsを開いたままページをリロードすると表示される可能性がある。
該当のデータをクリックし、レススポンスタブを開くと、JSONファイルの中を閲覧することができる。
これをコピペして「stats.json」のような名前でローカルのPCに保存しておく。
実験1
Pythonを使って分析を行う。具体的には3ポイントシュートの確率とフリースローの確率の相関係数を求めた。
そのコードが以下である。
import json
import pandas as pd
from matplotlib import pyplot as plt
# データを読み込む
with open('stats.json') as f:
response = json.load(f)
headers = response['resultSets'][0]['headers']
dataset = response['resultSets'][0]['rowSet']
df = pd.DataFrame(dataset, columns=headers)
print(f"条件を満たす選手の数: {len(df)}人")
# 散布図を描画
plt.scatter(df["FG3_PCT"], df["FT_PCT"])
plt.show()
# 相関係数を算出
df = df[["FG3_PCT", "FT_PCT"]]
corr = df.corr()
print(f"相関係数: #{corr}")
上記のコードを実行したところ、
条件を満たす選手の数: 539人
相関係数: 0.248
となった。散布図は以下。
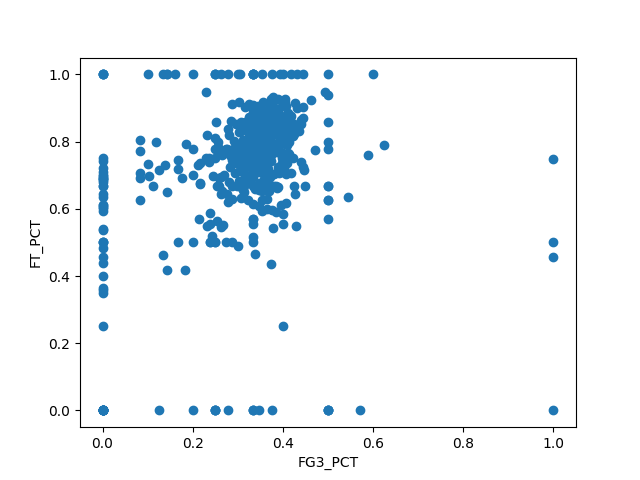
散布図を見ると、3ポイントシュートについてもフリースローについても、確率0%のデータと確率100%のデータが多くあることが分かる。これは出場機会がほとんど無く、3ポイントシュートやフリースローをほとんど放っていない(= 確率が収束するほどシュートを放っていないので両極端に振れている)選手が多数いることが原因だと考えられる。
そこで、実験2ではこれらのデータを外れ値として除外して相関係数を求めることにした。具体的には3ポイントシュートとフリースローをともに50本以上放っている選手のみを抽出して相関係数を求めた。
実験2
そのコードが以下である。
import json
import pandas as pd
from matplotlib import pyplot as plt
# データを読み込む
with open('stats.json') as f:
response = json.load(f)
headers = response['resultSets'][0]['headers']
dataset = response['resultSets'][0]['rowSet']
df = pd.DataFrame(dataset, columns=headers)
# 選手をフィルタリング
df = df[(df["FG3A"] >= 50) & (df["FTA"] >= 50)]
print(f"条件を満たす選手の数: {len(df)}人")
# 散布図を描画
plt.scatter(df["FG3_PCT"], df["FT_PCT"])
plt.xlabel("FG3_PCT")
plt.ylabel("FT_PCT")
plt.show()
# 相関係数を算出
df = df[["FG3_PCT", "FT_PCT"]]
corr = df.corr()
print(f"相関係数: #{corr}")
上記のコードを実行したところ、
条件を満たす選手の数: 246人
相関係数: 0.37073
となった。散布図は以下。
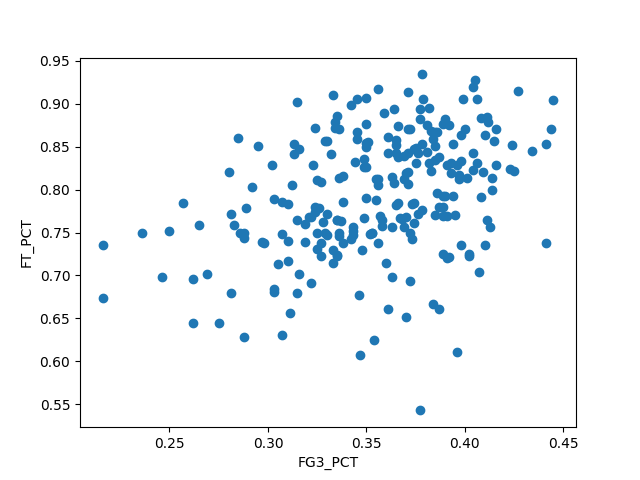
相関係数を求めるにあたって、246人分のデータで十分なのかが心配だったので、実験3では2022-23シーズンのデータに加えて、2020-21シーズンと2021-22シーズンのデータも結合して分析を行うことにした。
実験3
そのコードが以下である。
import json
import pandas as pd
from matplotlib import pyplot as plt
# データを読み込む
with open('stats20-21.json') as f:
response = json.load(f)
headers = response['resultSets'][0]['headers']
dataset = response['resultSets'][0]['rowSet']
df1 = pd.DataFrame(dataset, columns=headers)
with open('stats21-22.json') as f:
response = json.load(f)
headers = response['resultSets'][0]['headers']
dataset = response['resultSets'][0]['rowSet']
df2 = pd.DataFrame(dataset, columns=headers)
with open('stats22-23.json') as f:
response = json.load(f)
headers = response['resultSets'][0]['headers']
dataset = response['resultSets'][0]['rowSet']
df3 = pd.DataFrame(dataset, columns=headers)
# 3年分のデータを結合
df = pd.concat([df1, df2, df3])
# 選手をフィルタリング
df = df[(df["FG3A"] >= 50) & (df["FTA"] >= 50)]
print(f"条件を満たす選手の数: {len(df)}人")
# 散布図を描画
plt.scatter(df["FG3_PCT"], df["FT_PCT"])
plt.xlabel("FG3_PCT")
plt.ylabel("FT_PCT")
plt.show()
# 相関係数を算出
df = df[["FG3_PCT", "FT_PCT"]]
corr = df.corr()
print(f"相関係数: #{corr}")
上記のコードを実行したところ、
条件を満たす選手の数: 753人
相関係数: 0.346855
となった。散布図は以下。
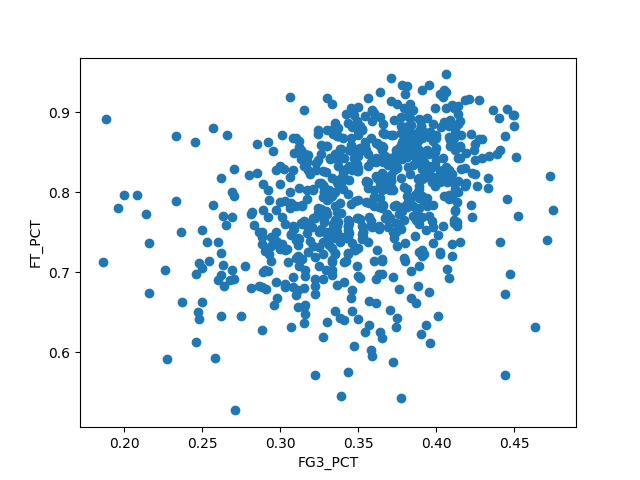
結論
相関係数は、各実験で以下のようになった。
実験1: 0.248
実験2: 0.37073
実験3: 0.346855
上記のボストン大学の資料では相関係数の目安が載っており、+0.2 ~ +0.4は弱い正の相関と定義されている。
したがって、3ポイントシュートの上手さとフリースローの上手さには弱い正の相関があると考えることができるであろう。
Discussion