素数関連のアルゴリズム
予備知識
エラストテネスのふるい
素数を求めるアルゴリズムとしてエラストテネスのふるいをとりあげます。
このアルゴリズムで出来ること
３～ある自然数までの素数をすべて求める
※素数とは「１とその数自身の他に約数を持たない正の整数」である
※０と１は素数ではない
※最小の素数は２である
動作順序
①素数を選定する ※まずは最小の素数２を使う
②３～ある自然数までの数字を①の倍数と①の倍数ではない数に分ける
③①の倍数ではない数の中で最小の数を新たに①として②に戻る
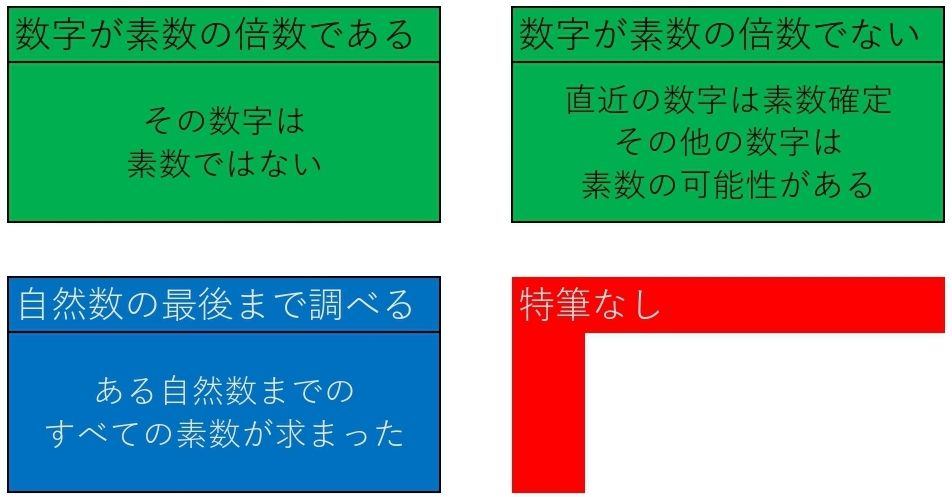
※ある自然数までに必ず素数が含まれるため特筆なしとする
※以降は「倍数ではない数」のことを「非倍数」と呼ぶこととする
計算対象選別
| 判定 | 計算対象 | 関係 | 数値 |
|---|---|---|---|
| ○ | データの比較回数 | = | 素数の倍数の個数 |
| データの交換回数 | = | なし | |
| 関数の呼び出し回数 | ≦ | 素数の個数 |
変数定義
| 変数にする対象 | 変数 | 関係 | 数値 |
|---|---|---|---|
| 自然数 | > | 1 | |
| 数列 |
一般化
例として３～４５までの計算量を求める
３～４５までの素数と計算量
３～４５について分ける手順を示していく
最小の素数２から始める
- ３～４５までの数を２の倍数と非倍数に分ける
素数２の次の素数は３であると確定する
※非倍数の中で最小のものが素数であると確定する - ３～４５までの数を３の倍数と非倍数に分ける
素数３の次の素数は５であると確定する - ３～４５までの数を５の倍数と非倍数に分ける
素数３の次の素数は７であると確定する
３～４５までの数を７の倍数と非倍数に分ける必要はない
なぜなら４５は７の２乗すなわち４９未満であるためである
例えば６×７は４２になる
同様に４９未満の数は２～６の倍数か素数となっているから
以上で３～４５までの数を素数の倍数と非倍数に分け終えた
ここで計算量は素数の倍数の個数になる
素数の倍数の個数は４５を各素数［２，３，５］で割った値の整数部分から素数自身を除いたものである
これはガウス記号を用いた床関数をつかって表せる
※ガウス記号の床関数とは実数に対するそれ以下の最大整数を表現するものである
※中括弧でも誤りではないが混同を避けたい場合は
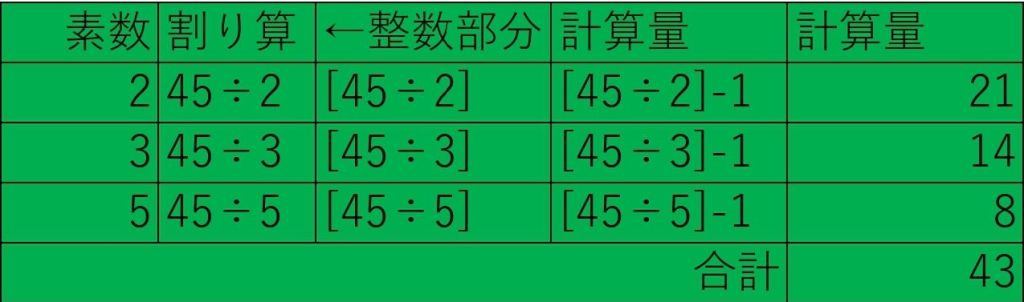
表と条件式による一般化
３～４５までの表を参考に
３からｎまでの計算量を表にすると
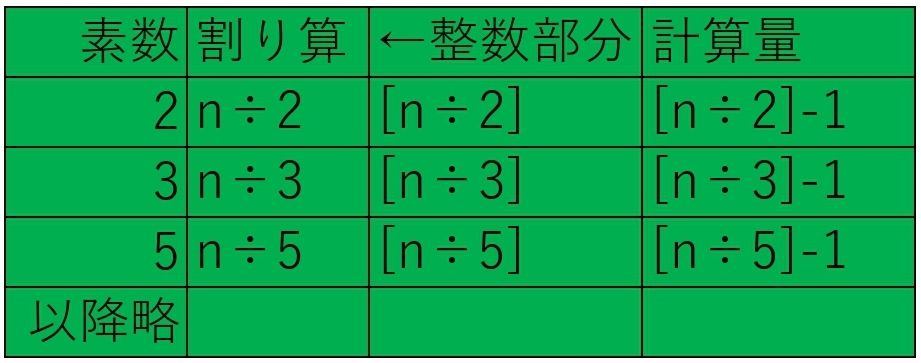
前項目での表現を一般化すると
「素数の倍数の個数は４５を各素数［２，３，５］で割った値の整数部分から素数自身を除いたものである」
↓
「素数の倍数の個数はｎを各素数［
最小の素数２を
以下の条件式を使ってｎが
その次の素数で確かめるなら式の
その次の素数で確かめるなら式の
その次の素数で…
３からｎまでの素数を求めるには
これら条件を満たす間おなじ処理を繰り返す
上記の表と条件式をもとにエラストテネスのふるいにおける合計計算量を求める
以上により３からｎまでの素数を求めることが可能である
※素数の個数は別途で数える必要がある
試し割り法
素因数分解のアルゴリズムとして試し割り法を紹介します。
このアルゴリズムで出来ること
ある自然数を素数の積の形まで分解する
※このときの素数を素因数と呼ぶ
※ある自然数に対する素因数は重複できる
動作順序
①自然数の約数を小さい順から探す
※自然数の約数は素因数である
②商が１の約数が求まった時点ですべての素因数が見つかる
※あらゆる自然数は素因数で表せるため特筆なしとする
計算対象選別
| 判定 | 計算対象 | 関係 | 数値 |
|---|---|---|---|
| データの比較回数 | = | 0 | |
| データの交換回数 | = | 0 | |
| ○ | 関数の呼び出し回数 | ≧ | 1 |
変数定義
| 変数にする対象 | 変数 | 関係 | 数値 |
|---|---|---|---|
| 自然数 | > | 1 |
一般化
例として自然数を４５としたときの計算量を求める
ある自然数を４５としたときの素因数分解と計算量
※３行目が割られる数、４行目が割る数、割り算の回数を計算量とする
※関数内で条件付き繰り返し処理を行えば計算量は１回で済むが、ここでは割り算の回数の違いを調べるために表のような書き方にしている
エラストテネスのふるいをつかって
すでに素数が求まっているとき
※整数行が素数行となり一部整数の試し割りが不要となる
※一部整数の試し割りが不要となるが、エラストテネスふるいで計算量が４３余分にかかってくる
文字式による一般化
計算量は自然数によって異なる
そのため計算量の文字式による一般化は省略する
Discussion