🎲

Python による確率分布の推定と描画

2024/06/10に公開

Python

データ解析

確率分布

tech

東工大情報理工学院高安研究室で開催されている新入生向けのプログラミングゼミの資料を一部公開します．

データ解析の現場では，データの統計的性質を把握するために確率分布を確認します．
本稿ではデータから確率分布を推定し，描画する方法を紹介します．

確率変数と確率分布

はじめに，確率変数について簡単に復習します．確率変数とは，どのような値となるかが確率的に定まっている変数です．数学的には全ての事象に数値を対応させる関数として定義され，各値にはその値を取る事象の割合が確率として乗っています．

全事象を $\Omega$ としましょう．確率変数 $X$ は全事象 $\Omega$ から数値 $E$ への写像 $X:\Omega \rightarrow E$ です．確率変数 $X$ によって値 $x$ に対応づけられる事象の集合は， $X$ による値 $x$ の逆像

X^{-1}(x) := \{ \omega \in \Omega \,|\, X(\omega) = x \} \subset \Omega

として表せます．確率変数 $X$ が値 $x$ を取る確率は，対応する事象の数の割合

P_X(x) := \frac{ \#X^{-1}(x) }{ \#\Omega } = \frac{ \#\{ \omega \in \Omega \,|\, X(\omega) = x \} }{ \#\Omega }

によって定義します．（ $\#$ は集合の大きさを表す記号）

簡単な例を用いて確率変数とその確率の定義を確認しましょう．サイコロを振って出る目 $X$ は確率変数です．全事象は $\Omega = \{1,2,3,4,5,6\}$ であり，確率変数 $X$ は各事象に対して順番に $\{1,2,3,4,5,6\}$ という数値を対応づけます．確率変数 $X$ の取る数値には事象が 1 つずつ対応するため，どの値も確率は $1/6$ です． $X$ の取る数値を基準にこれらを整理すると下記のようになります．

数値	1	2	3	4	5	6
対応する事象	1	2	3	4	5	6
対応する事象の数	1	1	1	1	1	1
確率	1/6	1/6	1/6	1/6	1/6	1/6

サイコロの出目を 2 で割った余り $X \% 2$ もまた確率変数です．取りうる値は 0,1 の 2 つであり，これらの値に対する事象や確率の対応表は次のようになります．

数値	0	1
対応する事象	2,4,6	1,3,5
対応する事象の数	3	3
確率	3/6	3/6

同じサイコロをもう 1 つ用意し，2 つのサイコロを振って出る目を $X, Y$ とすると，それらの和 $X+Y$ も確率変数になります．全事象は 2 つのサイコロの出目の組であり，下記のような36種類の組の集合として表せます．

\begin{aligned} \Omega = \big\{\, & (1,1),\, (1,2),\, (1,3),\, (1,4),\, (1,5),\, (1,6), \\ & (2,1),\, (2,2),\, (2,3),\, (2,4),\, (2,5),\, (2,6), \\ & (3,1),\, (3,2),\, (3,3),\, (3,4),\, (3,5),\, (3,6), \\ & (4,1),\, (4,2),\, (4,3),\, (4,4),\, (4,5),\, (4,6), \\ & (5,1),\, (5,2),\, (5,3),\, (5,4),\, (5,5),\, (5,6), \\ & (6,1),\, (6,2),\, (6,3),\, (6,4),\, (6,5),\, (6,6) \,\big\}\end{aligned}

$X$ の取るそれぞれの数値について，対応する事象とその数，確率を整理すると下記のようになります．

数値	2	3	4	5	6	7	8	9	10	11	12
対応する事象	(1,1)	(1,2) (2,1)	(1,3) (2,2) (3,1)	(1,4) (2,3) (3,2) (4,1)	(1,5) (2,4) (3,3) (4,2) (5.1)	(1,6) (2,5) (3,4) (4,3) (5.2) (6,1)	(2,6) (3,5) (4,4) (5,3) (6,2)	(3,6) (4,5) (5,4) (6,3)	(4,6) (5,5) (6,4)	(5,6) (6,5)	(6,6)
対応する事象の数	1	2	3	4	5	6	5	4	3	2	1
確率	1/36	2/36	3/36	4/36	5/36	6/36	5/36	4/36	3/36	2/36	1/36

確率変数が与えられたとき，取りうる値の対応する事象を列挙して確率を求めるのは面倒ですし，

一般に，確率変数の数値がどのように生成されたのか，すなわち，それぞれの数値にどの事象が対応しているのかにはあまり興味がありません．代わりに，数値と確率の対応関係に注目します．確率変数の数値に対して確率を対応させる関数を確率分布と言います．例えば，サイコロの出目 $X$ と，2 つのサイコロの出目の和 $X+Y$ の確率分布は下図のようになります．

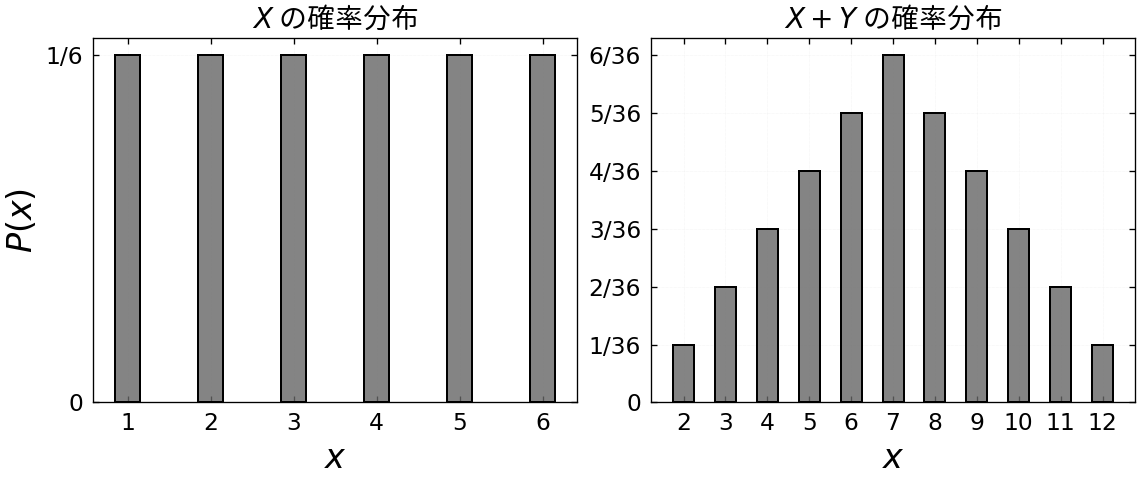
saikoro_prob

サイコロの例では確率変数の取る値が離散的でしたが，連続値を取る確率変数を考えることもできます．離散型の確率変数では各値に確率が対応しますが，連続型の確率変数では各値に確率密度が対応します（後述）．

確率分布

本章では，連続型の確率変数を想定して理論説明を行ないます

確率変数に対応する確率の見方として，確率密度関数 (Probability Density Function; PDF) と 累積分布関数 (Cumulative Density Function; CDF) の 2 つがあります．

累積分布関数 (CDF) の定義

確率変数 $X$ の累積分布関数 $F(x)$ は，次のような上側確率で定義します．

F(x) := P(X \geq x)

一般的には累積分布関数を下側確率 $P(X \leq x)$ で定義されますが，統計物理学（とそれを理論的土台とする社会経済物理学）分野では上側確率で定義する習慣があります．理由は，分野でよく登場する関数である指数分布やベキ分布を観察しやすいからです．

累積分布関数を上側確率で定義すると，

指数分布は $y$ 軸を log スケールとする片対数空間で，
ベキ分布は両対数空間で直線になります

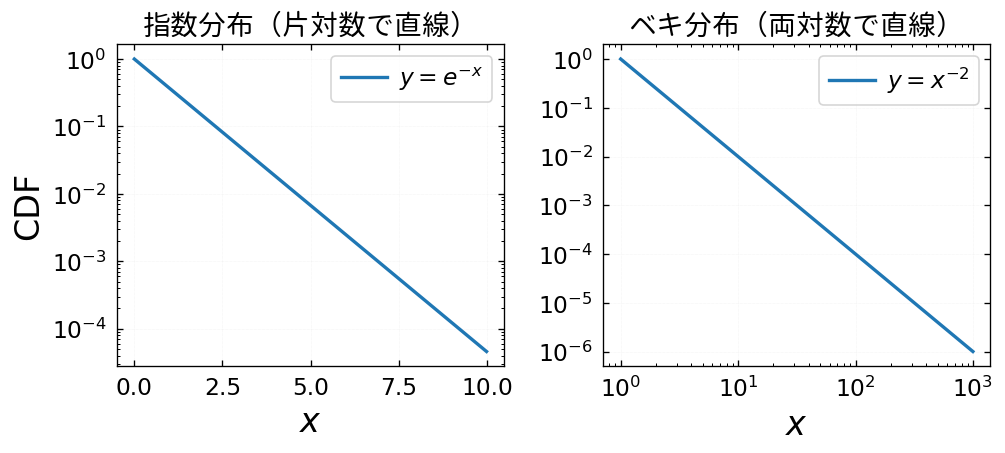
指数分布とベキ分布のCDF

指数分布の CDF が満たす性質

指数分布の CDF は

P(X \geq x) = e^{-\lambda x}\ ;\quad x \geq 0

で書けるので，

\log F = -\lambda x

を満たします．よって，指数分布の CDF は

y

軸を対数とする片対数空間で直線になります．

ベキ分布の CDF が満たす性質

ベキ分布の CDF は

P(X \geq x) = x^{-\alpha}\ ;\quad x \geq 1

で書けるので，

\log F = -\alpha \log x

を満たします．よって，ベキ分布の CDF は両対数空間で直線になります．

確率密度関数 (PDF)

確率変数 $X$ の確率密度関数 $f(x)$ は， $X$ の取りうる任意の区間 $[a,b]$ について

P(a\leq X \leq b) = \int_a^b f(x)\, dx

を満たす関数として定義されます．ただし，確率は非負であることと，その和が1であることから，

f(x)

は次の 2 つの条件を満たします．

すべての実数 $x$ に対して $f(x)\geq 0$
$\int_{-\infty}^\infty f(x)\, dx = 1$

確率「密度」と呼ばれる所以は， $X$ が微小区間 $[x,x+\delta x]\,(\delta x>0)$ を取る確率が

P(x\leq X \leq x+\delta x) \simeq f(x)\delta x

のように近似でき， $f(x)$ は確率を区間幅 $\delta x$ で割ったもの（密度）と理解できるためです．
また，この関係から

f(x) \simeq - \frac{P(X \geq x+\delta x)-P(X \geq x)}{\delta x} = - \frac{F(x+\delta x)-F(x)}{\delta x}

が導かれるので， $f(x) = -F'(x)$ の関係も自然と理解されます．

累積分布 $F(x)$ を下側確率で定義する場合は $f(x) = F'(x)$ の関係が成り立ちます．

確率分布の推定

確率変数 $X$ の実現値として，データ $D = (x_1,x_2,\dots,x_N)$ が得られたとします．この時， $X$ の CDF・PDF を推定する方法を紹介します．

累積分布関数 (CDF) の推定

$X \geq x$ となる確率を全データに占める $x$ 以上のデータの個数の割合で近似すれば，

P(X \geq x) \simeq \frac{\#\{i\ |\ x_i \geq x \}}{N} =: F_e(x)

のように累積分布を推定できます．データから得られる分布関数 $F_e(x)$ は経験分布関数と呼ばれ，真の分布関数 $F(x)$ と区別されます．データ数 $N$ が大きくなるほど $F_e(x)$ は $F(x)$ に近づくことが期待されます．経験分布の形状は，データの最小値から最大値にかけて，1 から $1/N$ 単位で下がる階段関数になっています．例えば，データに重複がなければ，最小値 $x_\mathrm{max}$ と最大値 $x_\mathrm{max}$ について

F_e(x_\mathrm{min}) = 1,\quad F_e(x_\mathrm{max}) = 1/N

が成り立ちます．最大値 $x_\mathrm{max}$ を取るデータが複数ある場合は，その個数を $N_\mathrm{max}$ と置くと

F_e(x_\mathrm{max}) = N_\mathrm{max}/N

となります．

$F_e(x_\mathrm{max})$ の例から分かるように，上記の $F_e(x)$ の定義ではデータに同じ値が含まれる場合に推定が少々面倒です．データ解析の現場では，データのソートで経験分布関数を求める下記の方法がよく用いられます．

データを大きい順に並び替える
ソートしたデータに対し，確率を $(1/N, 2/N,\dots,N/N)$ で割り当てる

ここで求まる経験分布は，同じ値に複数の値が対応する場合があり，厳密には関数ではありません．しかし，計算が簡単なことや，データから一意に定まること，データの右端の点が確率 $1/N$ に対応するため図からデータ数を見積もりやすい等の良さがあり，実用的です．

プログラムの例を示します．

def draw_cdf(x, xlabel=None, logx=False, logy=False):
    # calculation
    n = len(x)
    cdf = [(i+1)/n for i in range(n)]
    # plot
    plt.plot(sorted(x, reverse=True), cdf)
    plt.ylabel('CDF')
    if xlabel: plt.xlabel(xlabel)
    if logx: plt.xscale('log')
    if logy: plt.yscale('log')

確率密度関数 (PDF) の推定

ヒストグラム法

データから確率密度関数を推定する方法としては，ヒストグラム法がよく用いられます．ヒストグラムとは，データを区間に分け，区間の代表値を横軸に，区間内のデータ数を縦軸にとった図のことです．ヒストグラムはデータ数や区間幅を変えると縦軸が伸縮します．下図 (a),(b),(c) は標準正規分布からサンプルしたデータのヒストグラムです．3つの図の縦軸は比較しやすいよう揃えてあります．図から次の2点が確認できます．

データ数を増やすと (a→b) 各区間に入るデータの個数が増える
区間の幅を広げると (a→c) 各区間に入るデータの個数が増える

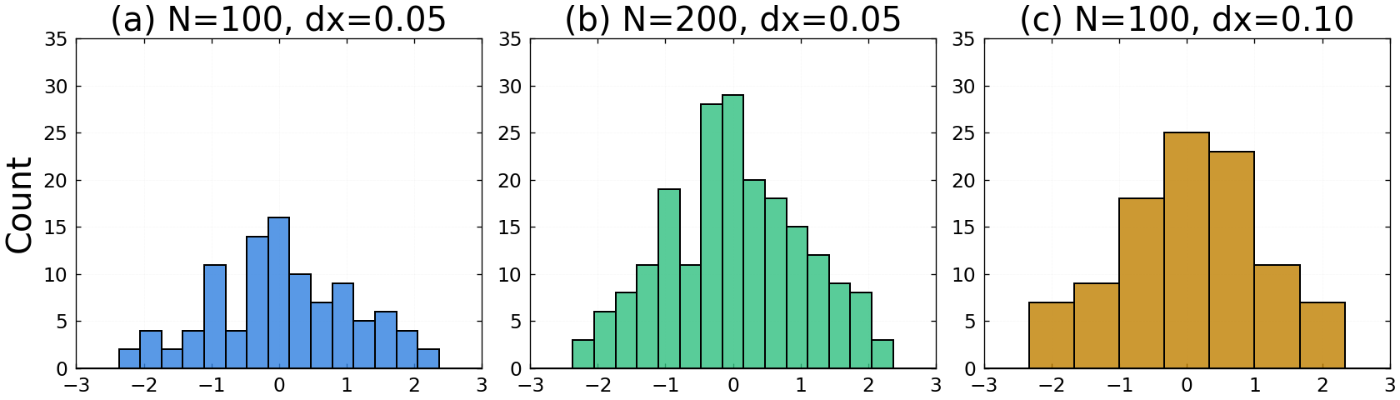
compare_histograms

データの背後にある確率分布は，データの個数や区間幅の取り方によらず一定です．そこで，ヒストグラムの縦軸をデータ数と区間幅で割ることで，面積の和が 1 になるよう規格化します．このように確率密度を推定する方法はヒストグラム法と呼ばれます．

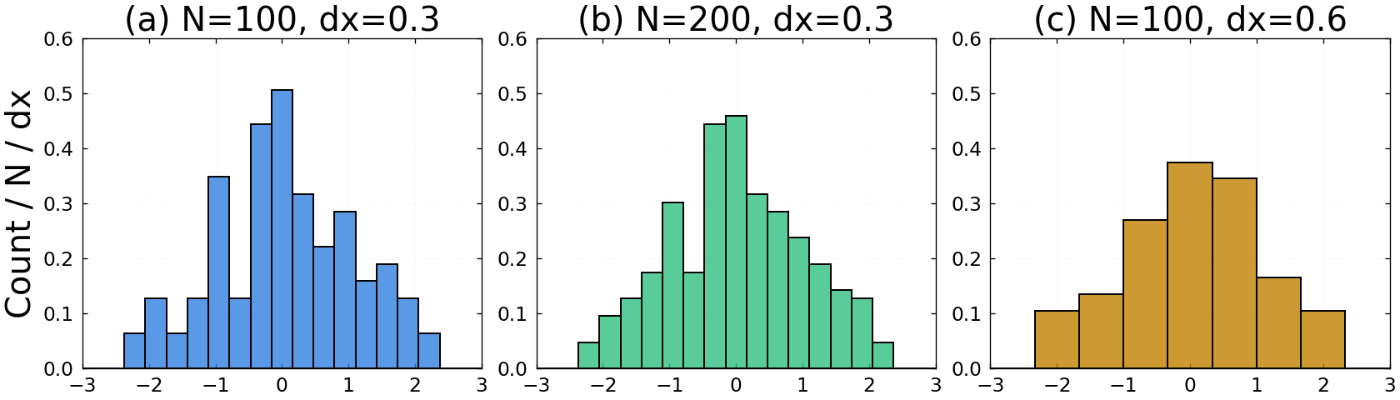
compare_histograms_density

ヒストグラム法における区間幅 $dx$ の取り方には任意性があり，描画の目的に応じて調整が必要です．調整の方針として，図からデータの最頻値や外れ値のような局所的な情報を読み取れるようにしたい場合は区間幅を小さく取り，分布の大まかな形状に興味がある場合は区間幅を大きく取るといった考え方があります．上図 (a),(c) を参考にしてください．描画に使用したデータは同じですが，区間幅の取り方によって確率密度の見え方と図に含まれるメッセージが変わることが分かります．

ヒストグラム法の数学的解釈

確率変数 $X$ が区間 $[x_i-\delta x/2, x_i+\delta x/2)$ に入る確率は，密度関数 $f$ を用いて

P(x_i-\delta x/2\leq X \leq x_i+\delta x/2) \simeq f(x_i)\,\delta x

のように近似できます．一方で，区間に入るデータ数を $N_i$ を用いて

P(x_i-\delta x/2\leq X \leq x_i+\delta x/2) \simeq \frac{N_i}{N}

とも近似できます．これらを合わせれば

f(x_i) \simeq \frac{N_i}{N\, \delta x}

の関係が得られます．この右辺がヒストグラム法によってデータから求まる（経験）確率密度関数に対応します．

ヒストグラム法の実装

ヒストグラムの左端の点 $x_\mathrm{min}$ と区間幅 $\delta x$ を決める
- 左端の区間は $I_0 = [x_\mathrm{min}, x_\mathrm{min}+\delta x)$
- 左から $i\,(=0,1,2,\dots)$ 番目の区間は $I_i = \big[x_\mathrm{min}+i\,\delta x, x_\mathrm{min}+(i+1)\,\delta x\big)$
- 区間 $I_i$ の代表値は $x_i = x_\mathrm{min}+(i+\frac{1}{2})\,\delta x$
各データ点を区間に対応させる
$\mathrm{Data} \ni x\ \longmapsto\ i = \left\lfloor \frac{x - x_\mathrm{min}}{\delta x} \right\rfloor$
各区間に入っているデータの数を数える
区間内のデータ数を $N\,\delta x$ で割って正規化する

プログラムの例を示します．

# ヒストグラム法による PDF の推定
def calc_pdf(x, xmin=None, dx=1.0):
    if not xmin: xmin = min(x)
    # xmin: ヒストグラムの左端の点（None なら最小値を使う）
    # dx  : 区間幅
    
    x = pd.Series(x)
    indices = np.floor((x-xmin)/dx) # 切り捨て

    pdf = indices.value_counts(normalize=True) / dx
    pdf.index = xmin + dx/2 + pdf.index*dx
    pdf = pdf.sort_index() # 折れ線プロットする場合に必要
    return pdf

# PDF を棒グラフで描画
def draw_pdf(x, xmin=None, dx=1.0, xlabel=None, logy=False):
    pdf = calc_pdf(x, xmin=xmin, dx=dx)
    plt.bar(pdf.index, p.values, width=dx, lw=1.5, ec='k')
    plt.ylabel('PDF')
    if xlabel: plt.xlabel(xlabel)
    if logy: plt.yscale('log')

データの要素数を数える pandas.Series.value_counts 関数はよく使うので，覚えておくと良いです．
辞書ベースのデータ構造を使って要素数を数えているため，PDF にデータ数 0 の区間は含まれません
plt.bar 内のパラメータ lw(linewidth), ec(edgecolor) は適宜調整してください
plt.hist(x, density=True) でも PDF を描画できます．ただし，用法を十分確認してください（参考：matplotlib.pyplot.hist）

PDF を折れ線プロットする際の注意点

PDF にデータ数 0 の区間が含まれず，代表値が飛び飛びになる場合があること

上述のプログラムでは PDF を棒グラフ (plt.bar) で描画していますが，折れ線グラフ (plt.plot) で描画することも可能です．棒グラフによる描画は区間幅が分かりやすいですが，見やすい図を作るには fc(facecolor), lw, ec 等のパラメータを調整する必要があり，少々面倒です．折れ線グラフはパラメータの細かい調整が必要ありません．しかし，折れ線グラフの「隣合う2点間の値を線形補完する性質」は，中間に確率密度 0 の区間がある場合に誤った情報を提示する可能性があります．例えば下記のような場合に注意が必要です．

区間幅を小さく設定する場合
データ数の少ない領域
外れ値がある場合
他峰型の分布

外れ値がある場合と二峰型の分布で例示します．下の二つ図はどちらも同じ PDF を plt.plot と plt.bar で描画したものです．左図の $3\leq x \leq 7$ 領域と右図の $3\leq x \leq 4$ 領域の付近は，どちらも確率密度の推定値が 0 です．これらの情報は棒グラフでは正しく伝わりますが，折れ線グラフでは左右の値によって線形補完された確率密度が表示され，あたかもデータが存在しているように伝わります．

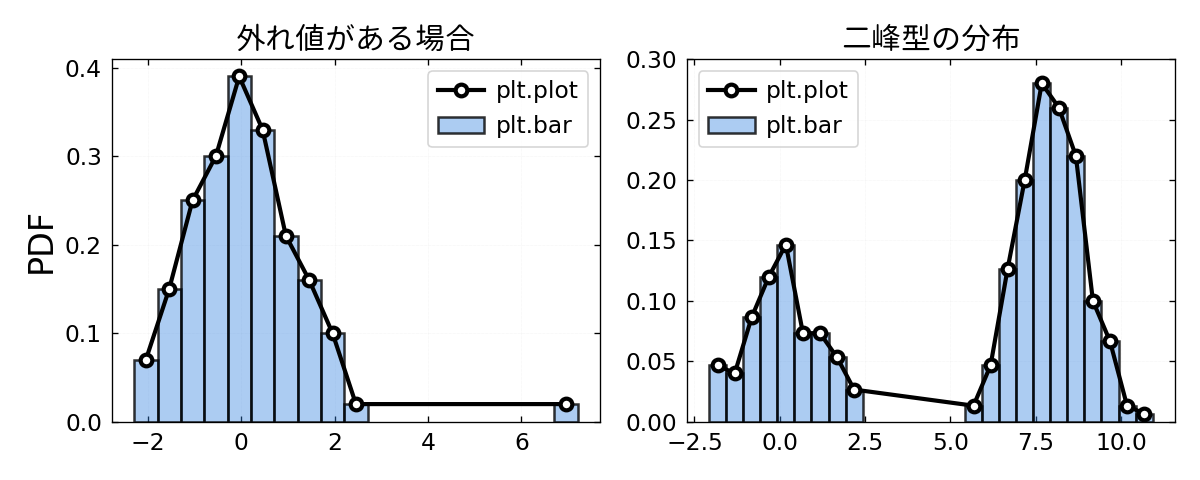
dist_pdf_caution

点にマーカーを付けないといっそう情報の正確性が失われます（下図）．特に左図では，値 7 を外れ値として識別できなくなっています．

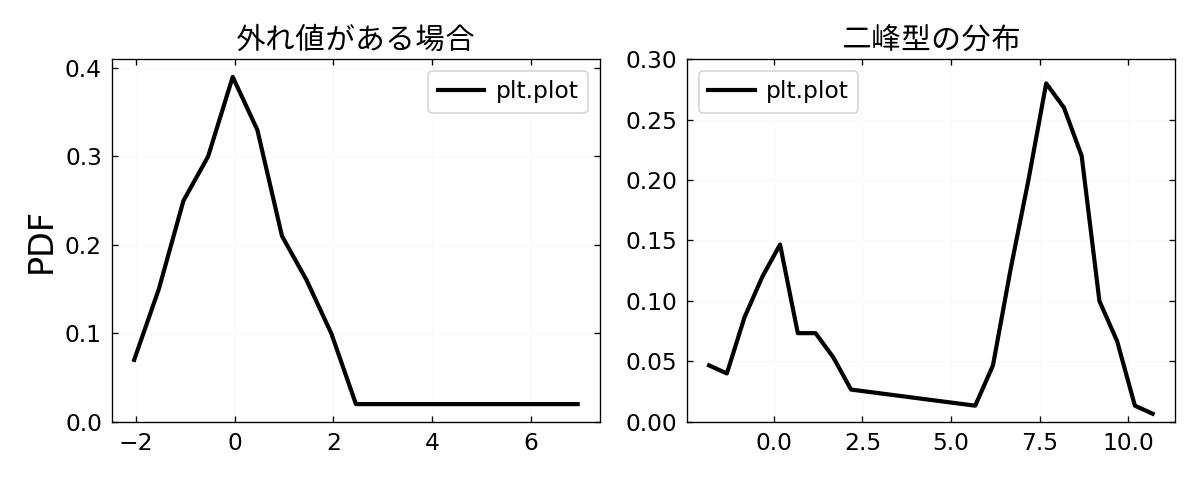
dist_pdf_caution_only_line

対策として，次の3つが考えられます．

点にマーカーを付けるだけで妥協する（厳密性不要 & パパッと分布を確認したい時）

中間の確率密度 0 の区間を追加する

pdf = calc_pdf(x, dx=dx)
# pdf.index : 各区間の代表値
# pdf.values: 各区間の確率密度

# 確率密度 0 の区間を追加
indices_filled = np.arange(pdf.index.min(), pdf.index.max()+dx, dx)
zeros = pd.Series(index=indices_filled, data=np.zeros(len(indices_filled)))
pdf = (pdf + zeros).fillna(0) # index が異なる部分の和は NaN になるので 0 埋めする

PDF を配列ベースのデータ構造で定義してヒストグラム法を書き直す（課題）

PDF を経由して CDF を求める方法は非推奨

ヒストグラム法で推定した PDF を累積すれば CDF を求めることはできますが，実際にはあまり使われません．理由は次の2点です．

単純に面倒
PDF の区間の取り方によって CDF の描像が変わる

CDF を描く際は上述した方法を用いてください．

CDF と PDF の特長比較

CDF と PDF を比較してそれぞれの特長を述べます．

CDF の特長

簡単に描ける
傾きからパラメータを大雑把に見積れる
「x 以上のユーザーは 100y %しかいない」等の割合の議論がしやすい
ミスに気づきやすい（左端の y 座標は必ず1，右端の y 座標は 1/N，N はデータ数）

PDF の特長

局所的な情報（最頻値や山の位置，異常値など）を把握しやすい
正負の両側に裾を持つ分布（正規分布，成長率分布として頻出するラプラス分布など）に向いている

課題（実データの分布推定）

約 20,000 曲の楽曲データ Spotify and Youtube について，

好きな変数をいくつか選び，CDF・PDF を描画して分布の形状や特徴を議論してください
データは人気曲に限定されていますが，世の中に存在する全ての楽曲を対象とした場合に，各変数の分布がどのようになるか考えてください

補足

確率分布の例：一様分布，正規分布，対数正規分布，指数分布，ベキ分布

データの説明

約 2,000 人のアーティストを対象に，YouTube の公式 MV の再生数上位10曲を抽出したデータ
YouTube の動画情報に加え，Spotify から楽曲情報を取得してマージされている
YouTube の動画情報の例：Title, #Views, #Likes, #Comments (#A = number of A)
Spotify の楽曲情報の例：Duration (ms), Tempo, Key, Danceability, #Streams

データ読み込み： pandas.read_csv でそのまま読み込めます．

import pandas as pd
data = pd.read_csv('Spotify_Youtube.csv')

データには 28 個のコラムがあり，半数以上に欠損値が含まれています（下記 data.info() の出力を参照）．欠損の意味を考え，適当に処理してください．

# data.info() の出力
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 20718 entries, 0 to 20717
Data columns (total 28 columns):
 #   Column            Non-Null Count  Dtype  
---  ------            --------------  -----  
 0   Unnamed: 0        20718 non-null  int64  
 1   Artist            20718 non-null  object 
 2   Url_spotify       20718 non-null  object 
 3   Track             20718 non-null  object 
 4   Album             20718 non-null  object 
 5   Album_type        20718 non-null  object 
 6   Uri               20718 non-null  object 
 7   Danceability      20716 non-null  float64
 8   Energy            20716 non-null  float64
 9   Key               20716 non-null  float64
 10  Loudness          20716 non-null  float64
 11  Speechiness       20716 non-null  float64
 12  Acousticness      20716 non-null  float64
 13  Instrumentalness  20716 non-null  float64
 14  Liveness          20716 non-null  float64
 15  Valence           20716 non-null  float64
 16  Tempo             20716 non-null  float64
 17  Duration_ms       20716 non-null  float64
 18  Url_youtube       20248 non-null  object 
 19  Title             20248 non-null  object 
 20  Channel           20248 non-null  object 
 21  Views             20248 non-null  float64
 22  Likes             20177 non-null  float64
 23  Comments          20149 non-null  float64
 24  Description       19842 non-null  object 
 25  Licensed          20248 non-null  object 
 26  official_video    20248 non-null  object 
 27  Stream            20142 non-null  float64
dtypes: float64(15), int64(1), object(12)
memory usage: 4.4+ MB

欠損処理の方法例

落とす：pandas.Series.dropna
埋める：pandas.Series.fillna

Key には 0~11 の数値が格納されています．英語名・イタリア語名（ドレミ）との対応は次の通りです．

Key 番号	0	1	2	3	4	5	6	7	8	9	10	11
英語名	C	C♯/D♭	D	D♯/E♭	E	F	F♯/G♭	G	G♯/A♭	A	A♯/B♭	B
伊語名	ド	ド♯/レ♭	レ	レ♯/ミ♭	ミ	ファ	ファ♯/ソ♭	ソ	ソ♯/ラ♭	ラ	ラ♯/シ♭	シ

Mode (= major/minor) 情報は残念ながら本データセットには含まれていないため，Key/Mode の使用率分析はできません．Spotify API からは取得できるようなのですが......

YouTube の動画タイトルや概要欄の文字数は次のようなプログラムで取得できます．

# どちらも同じ
title_length = data['Title'].dropna().str.len()
title_length = data.Title.dropna().str.len()

特にこだわりがない場合は，Key, Tempo, Duration_ms, Views 等のコラムを分析してみてください．

発展課題（ヒストグラム法の拡張）

対数軸で等間隔になるように区間を定めるヒストグラム法を実装してください
- 対数軸での区間幅を $\delta l$ とすると，対数軸での区間 $[\log x-\delta l/2, \log x+\delta l/2)$ の線形軸での区間幅は
  $\delta x = e^{\log x+\delta l/2} - e^{\log x-\delta l/2} = x\,(e^{\delta l/2} - e^{-\delta l/2})$
  のように求まります．この $\delta x$ を使ってヒストグラムを正規化してください．
- $\delta l \ll 1$ の場合は $e^{\delta l/2}$ を一次近似し，
  $\delta x \simeq x\,\delta l$
  としても構いません．こちらの方が実装は楽です．
PDF を配列ベースのデータ構造で定義してヒストグラム法を実装してください
- Python 標準の list ではなく，numpy 配列を使用してください
- 区間の数 $\lceil \frac{x_\mathrm{max}-x_\mathrm{min}}{\delta x} \rceil$ が多すぎる場合には，計算を途中で終了するか，error を出した方が良いでしょう．
```
if (num_intervals > threshold)
    message = f'No. of intervals exceeds {threshold}'
    # 例1) コメントを残して計算を終了する
    print(message)
    return
    # 例2) Error を発生させる
    raise ValueError(message)
```

確率変数と確率分布

確率分布

累積分布関数 (CDF) の定義

指数分布の CDF が満たす性質

ベキ分布の CDF が満たす性質

確率密度関数 (PDF)

確率分布の推定

累積分布関数 (CDF) の推定

確率密度関数 (PDF) の推定

ヒストグラム法

ヒストグラム法の数学的解釈

ヒストグラム法の実装

PDF を折れ線プロットする際の注意点

PDF を経由して CDF を求める方法は非推奨

CDF と PDF の特長比較

CDF の特長

PDF の特長

課題（実データの分布推定）

補足

発展課題（ヒストグラム法の拡張）

Discussion