✨

【最適解も二乗オーダーなのかーーい】パスカルの三角形は動的計画法というアルゴリズムらしい

2025/11/08に公開

 解いた問題leetcode 118. Pascal's Triangle

パスカルの三角形をプログラミングで書こうねってやつ（雑

 学び最適解も2乗オーダーになることもある
動的計画法が何かを知れた
固定値があるならそれでいったん初期化して、変更が必要な部分だけ計算しなおせばいい

[1] * (i+1)で指定要素数をもつリストの初期化ができ、out of range対策しながら簡素にリストを書ける

 最初に考えた解法 first.py
class Solution:
    def generate(self, numRows: int) -> List[List[int]]:
        if not numRows:
            return None
        list = []
        lists = {}
        for i in range(numRows):
            lists[f"list_{i}"] = []
            
            if i >= 3:
                for j in range(1, i-1):
                    lists[f"list_{i}"][j] = lists[f"list_{i-1}"][j-1] + lists[f"list_{i-1}"][j]

            else:
                lists[f"list_{i}"][0] = 1
                lists[f"list_{i}"][-1] = 1
            list.append(lists[f"list_{i}"])
        
        return list
上から二つ目の段までは何も考えず1入れればいいし、それ以降も端は1を入れればいい。

3段目からは一つ上の段の同じインデックス+1つ前のインデックスの値が入るからそれらを愚直に実装してみた。
index out of rangeでエラー。lists[f"list_{i}"][0] で空のリストの0番目を指定しているのがいけないっぽい。修正
 second.py
class Solution:
    def generate(self, numRows: int) -> List[List[int]]:
        if not numRows:
            return None
        list = []
        lists = {}
        for i in range(numRows):
            lists[f"list_{i}"] = [1] * (i + 1)
            
            if i >= 3:
                for j in range(1, i-1):
                    lists[f"list_{i}"][j] = lists[f"list_{i-1}"][j-1] + lists[f"list_{i-1}"][j]

            else:
                lists[f"list_{i}"][0] = 1
                lists[f"list_{i}"][-1] = 1
            list.append(lists[f"list_{i}"])
        
        return list
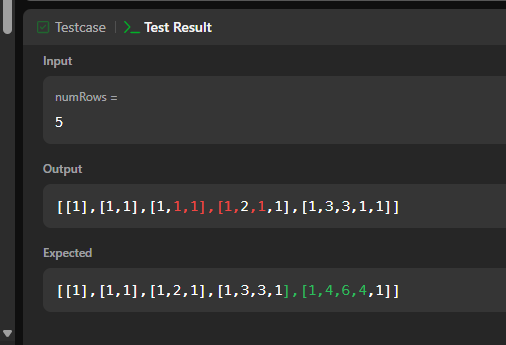
動いたが結果がおかしいのでNG

i-1やらif i >= 3やらの境界条件がおかしそうなので修正。
 third.py
class Solution:
    def generate(self, numRows: int) -> List[List[int]]:
        if not numRows:
            return None
        list = []
        lists = {}
        for i in range(numRows):
            lists[f"list_{i}"] = [1] * (i + 1)
            
            if i >= 2:
                for j in range(1, i):
                    lists[f"list_{i}"][j] = lists[f"list_{i-1}"][j-1] + lists[f"list_{i-1}"][j]

            else:
                lists[f"list_{i}"][0] = 1
                lists[f"list_{i}"][-1] = 1
            list.append(lists[f"list_{i}"])
        
        return list
うまくいった～～！

嬉しい。

でもこれO(N^2)くさいよなと思い答えを見てみた。

 答え answer.py
def generate(numRows: int) -> List[List[int]]:
    triangle = []
    for i in range(numRows):
        row = [1] * (i + 1)
        for j in range(1, i):
            row[j] = triangle[i-1][j-1] + triangle[i-1][j]
        triangle.append(row)
    return triangle
i=2のところも変に考えず前段の足し算で考えればよかったのか。

もともとi=3からjを回さないとと考えていたからおかしくなったけど、i=2から、と考えていたら最適解を最初に出せていたのかも、、、
これは動的計画法といって、各値を前の行の結果を使って再帰的に計算するアルゴリズムに分類されている。

再利用して効率的に構築し、冗長な計算を避けることができるそう。

 感想最適解もO(n^2)なんかーーーい
コードが冗長だったとはいえある程度アルゴリズムが想像できるようになってうれしい。

これからもちょくちょく進めます。

解いた問題

学び

最初に考えた解法

答え

感想

Discussion