線形計画法による最大マッチングアルゴリズム

はじめに

こんにちは。ZENKIGENデータサイエンスチーム所属のredteaです。原籍はオムロンソーシアルソリューションズ株式会社 技術創造センタですが、社外出向でZENKIGENに所属しており、数理最適化や機械学習を用いたデータの分析業務、それらの結果に基づいた顧客への提案をしております^[1]。

本記事の話題

先日、弊社ZENKIGENは、チームを超えた対話機会を生み出すシャッフルトークサービス「ENTAS(エンタス)」のベータ版を提供開始しました。ENTAS公式サイトはこちらです。

https://en-tas.jp/

本サービスは、従業員情報を元に、普段は話す機会の少ないメンバー同士をマッチングさせ、カレンダーへの予定入力まで自動で行うことで、手軽に継続的に会話の場をセッティングすることが可能です。私はこのマッチングアルゴリズム部分を担当しました。

本記事では、このマッチングアルゴリズムについて説明します。
具体的には、グラフ理論に基づいたマッチングアルゴリズムでは計算量が悪いため、線形計画法を用いて計算を工夫した話をします。

途中でマッチングに関する細かい理論にも言及します。丁寧に解説しますので、マッチングの理解を深めていければと思っています。なお、線形計画法については詳しく扱いませんので、線形計画法について詳しくない方は、例えば以下の記事・資料をご参照ください。

https://manabitimes.jp/math/930

http://www.me.titech.ac.jp/~mizu_lab/text/PDF-LP/LP1-problem.pdf

マッチング

まずはマッチングと最大マッチングについて、数学的な意味の確認から始め、ENTASで実現したいマッチングとはどんなマッチングかについて簡単に説明します。

最大マッチングとは

まずは単なるマッチングの説明からです。マッチングとは、グラフ理論で、どのノード(点)も2エッジ(辺)以上と繋がっていない部分グラフを意味します。

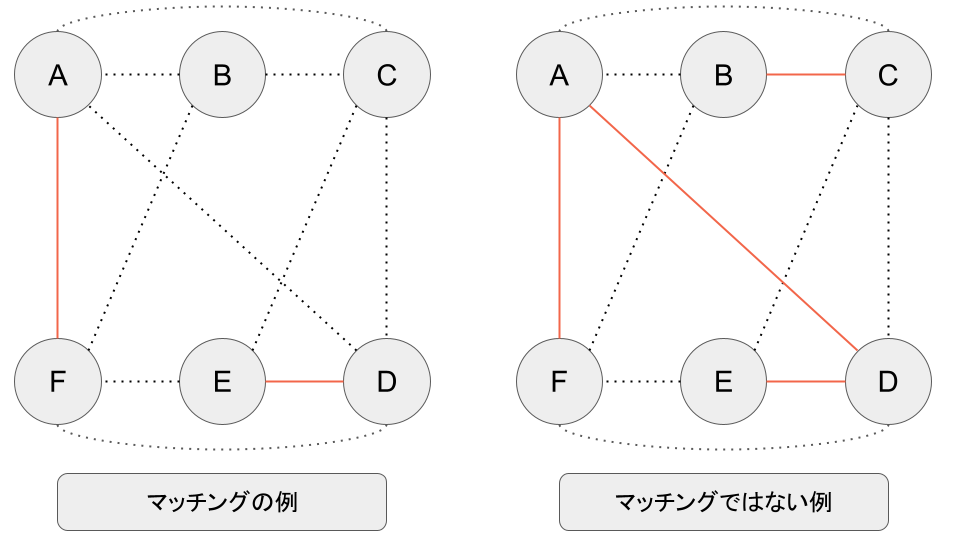
マッチングとマッチングではない部分グラフの例。点線は元のグラフのエッジを表し、オレンジ実線がマッチングを構成するエッジとします。マッチングではない例（図右）では、AとDがそれぞれ2辺持っているので、マッチングではなくなっています。

単なる「マッチング(matching)」では、3人以上のグループさえ作らなければマッチングと呼んで良いのですが、今回は余りをできるだけ少なくしたい（例えばペアを組めるはずの2人が余っている状況や、ペアを作り替えればより多くのペアが作れる状態を作りたくない）です。「最大マッチング(maximum cardinality matching)」というと、可能な限りたくさんのペアが作れている状態という意味になります。

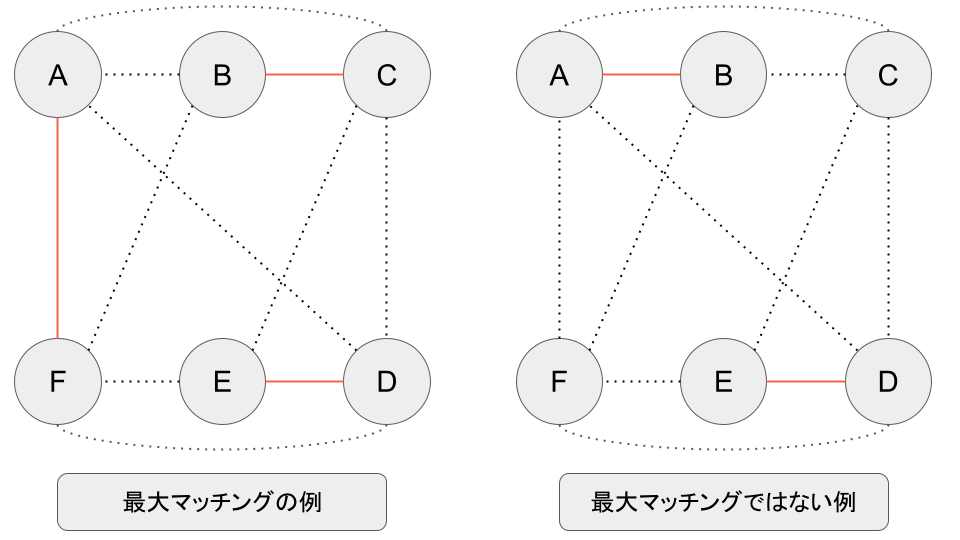
最大マッチングと最大マッチングではない部分グラフの例。点線は元のグラフを表し、オレンジ実線がマッチングを構成するエッジとします。最大マッチングではない例（図右）では、ペア数が2であるため、最大マッチングの例(図左)のペア数3より少ないです。

今回は、人をノードとし、マッチングしても良い人同士をエッジで結んだグラフを想定します。このエッジには重みがついています。例えばAさんは過去にBさんとシャッフルトークしたことがあればマッチングの必要性は低く、AさんとBさんの間のエッジ重みは小さくなったり、AさんとCさんは普段あまり話さない間柄であれば、話す機会を増やすためにAーCエッジの重みは大きくなったりします。

すなわち、ENTASのマッチングで実現したいことは、

マッチングしたノード間のエッジ重みの合計が最大になるように、最大マッチングを構成すること

です。

ENTASにおける良いマッチングとは

まずは良いマッチングとは何かを決めなければなりません。ENTASでは、普段話さないメンバー同士で話すことで、チームや部門を越えたコミュニケーションをつくることを目指しています^[2]。例えば以下のような条件を考慮します。

• AさんとBさんは同じ部署の人同士で、普段からよくコミュニケーションが取れているのでわざわざシャッフルトークで話す必要はない (所属条件)。
• AさんとDさんは以前シャッフルトークでマッチングしたことがあるので、2回目はもう少し経ってからで良い (履歴条件)。

これらの条件は、優先度に応じて設定することで、各人同士がマッチングした時の嬉しさを数値化し、マッチング重み行列$W$を作れば良いです。本記事では、マッチング重み行列$W$の作り方の説明は割愛し、$i$さんと$j$さんがマッチングしたときの嬉しさ$w_{i,j}$は既知であるものとします(行列$W$の$(i,j)$成分を$w_{i,j}$と表記します)。

ENTASマッチングの制約

ENTASのマッチングには、できるだけ満たしたい条件だけでなく、必ず満たしたい条件も存在します。例えば、AさんとCさんは、今は部署は違うものの、毎日MTGする間柄なので、シャッフルトークの必要性が全くありません。こういう場合にはNG条件^[3]とし、絶対にマッチングしないようにします。

最大マッチングのアルゴリズム

ここからはENTASのマッチングアルゴリズムについて説明します。

有名な最大マッチングアルゴリズムとして、Edmondsアルゴリズムというものがあります。これを用いることで、一般の^[4]重み付きグラフで、必ず最大マッチングを見つけることができます。

ただし、この重み和が最大となる最大マッチングを見つけるアルゴリズムの計算量は、シャッフルトーク参加人数を$N$とすると、$O(N^3)$です。大企業^[5]がシャッフルトークを実施するとなると、$N=1000$以上を想定しなければならないため、思いの外時間がかかってしまうことがあります^[6]。

そこで、より高速に動作するアルゴリズムの検討を行い、その結果、線形計画法を用いることで、効率良く重み和が最大となる最大マッチングを見つけられることがわかりました。線形計画法を用いれば、多項式計算量で解くことができますし^[7]、グラフを用いたアルゴリズムとは異なり、途中で探索を打ち切ることで、制約条件を満たしつつ、打ち切るまでに見つけた中で最良のマッチング結果を得ることができます^[8]。本章からは、重み和が最大となる最大マッチングを線形計画法で解く方法を紹介します。

最大マッチングを解く難しさ

エッジ重み和が最大となる最大マッチング^[9]を線形計画法で解くとは、何を制約にして、目的関数として何を最大化するかを決めることです。エッジ重み和を最大にしながら最大マッチングを目指すので、目的関数の設計では、エッジ重み和とペア数を勘案する必要がありそうですが、今回、エッジ重み和最大の最大マッチングを線形計画法で解く際の難しいポイントは、

NG条件が多い時、エッジ重み和を最大化することと、最大マッチングを構成することが相反する場合があること

です。

例えば以下の図のような場合を考えます。NG条件では、特定の2人をマッチングさせてはいけないので、その組間にはエッジが存在しないものとして扱います。以下の図では、エッジはA-C、A-D、B-Dの3つしかなく(マッチング可能)、A-B、B-C、C-Dの各組はNG条件(マッチング不可能)に該当します。

エッジ重み和の最大化と最大マッチングが両立しない例。

このグラフにおいて、A-C、B-Dでペアを作れば2組できますが(これが最大マッチング)、この時のエッジ重み和は$1+1=2$です。一方、最大マッチングではないものの、A-Dでペアを作ると(1組のみ)、エッジ重み和は5となり、最大マッチングではないもののエッジ重み和は最大という状況が生じることがわかります。

このように、エッジ重み和最大化と最大マッチングが両立しない可能性があるのはどんなときでしょうか？それは、NG条件が存在するときです。NG条件が存在しないときというのは、全員が自分以外の誰とでもペアを組んでも良い状況なので、任意の2ノード間にエッジが存在することになります^[10]。上図の例で、もしNG条件がなければ、B-C間にエッジ重みが0より大きな値^[11]を持つエッジが存在することになり、そのBとCをマッチングさせることでエッジ重み和を大きくさせながら、最大マッチングにすることができます。

一般的な表現をすると、NG条件が存在しないとき、「エッジ重み和が最大 $\rightarrow$ 最大マッチング」が成立します^[12]。 しかし、NG条件が存在する場合、この命題は成り立たず^[13]、線形計画法において単純にエッジ重み和を最大にするような目的関数を設定してしまうと、上図のように、最大マッチングではないエッジ重み和最大のマッチング結果になってしまう恐れがあります。

最大マッチング問題の線形計画法による定式化

シャッフルトーク参加者数を$N$とします(簡単のため$N$は偶数とします)。$N \times N$の行列$W$を、マッチング重み行列と呼び、対角成分が0で、非対角成分の要素が0より大きい値をとるものとします。$i$行目$j$列目の要素を$w_{i, j}$とすると、$w_{i, j}$は、$i$さんと$j$さんがマッチングした時の嬉しさ（高い方が望ましい）とします。本節の線形計画法の制約条件にも記載していますが、$w_{i,j}=w_{j,i}$とします^[14]。

また、マッチング行列$X$を、$i$さんと$j$さんがマッチングしている時^[15]、$x_{i, j}=1$であり、マッチングしていない時は$x_{i, j}=0$となる、要素に0または1しか値をとらない行列とします($X$のサイズも$N \times N$です)。
今回考案した線形計画法は、以下のとおりです。マッチング重み行列$W$が既知のとき、

目的関数

$$\max_{{X \in \{0,1\}}^{n \times n}} \sum_{i}\sum_{j} w_{i,j} x_{i,j} + \lambda \sum_{i}\sum_{j}x_{i,j} \\ \lambda = N \max_{i,j}w_{i,j}$$

制約条件

制約条件	補足
$x_{i,j} \in \{0,1\}$	$i$と$j$がマッチングしているかどうかを0と1で表現する。
$\forall i, \sum_{j} x_{i,j} \leq 1$	$i$は1以下のエッジしか持たない(1人以下としかペアを組めない)。
$\forall j, \sum_{i} x_{i,j} \leq 1$	$j$は1以下のエッジしか持たない(1人以下としかペアを組めない)。
$\forall i, x_{i,i} = 0$	自分同士とはペアを組めない。
$\forall i,j, x_{i,j}=x_{j,i}$	$i$と$j$がペアを組んでいるなら、$j$と$i$もペアを組む。
$(p,q) \in NG, x_{p,q}=0$	$p$と$q$がNGペアに指定されているなら、その2人はペアを組めない(グラフ上で$p$と$q$にエッジが存在しないことに相当)。

を解くことで、エッジ重み和を最大にしつつ、最大マッチングを表す行列$X$を得ることができます。目的関数の第一項$\sum_{i}\sum_{j} w_{i,j} x_{i,j}$ は、エッジ重み和を最大にしようとしており、第二項$\lambda \sum_{i}\sum_{j}x_{i,j}$は、マッチング数を最大にするための項です。それらの詳細は次の章で展開します。

最大マッチングの保証

本章では、前章で紹介した線形計画法を用いることで、最大マッチングが実現できる理由を説明します。

最大マッチングであるための条件

まずは最大マッチングについて詳しく理解します。

マッチング$M$について、$|M|$を$M$のエッジの数(マッチングのペア数)とします。あるグラフ$G=(V, E)$^[16]におけるマッチング$M$が最大マッチングである必要十分条件は、

AUGMENTING PATH(=増加道)が存在しないこと^[17]

です。

マッチング$M$について、以下の条件を満たす時、道^[18] $P$は増加道^[19]であると呼びます。

• $P$の出発点と到着点がマッチングの端点ではない
• 交互道である（$M$に含まれているエッジと含まれないエッジを交互に使う）

増加道が見つかれば、$M$を「反転」(マッチングで使っているエッジと使っていないエッジを入れ替え)することで、ペア数が多いマッチング$M'$を見つけることができます。イメージは以下のとおりです。黒点線が元のグラフのエッジ、オレンジ線がマッチングを表しています。

$M$に増加道が存在すれば、$M$よりもペア数が多いマッチング$M'$が存在するイメージ。

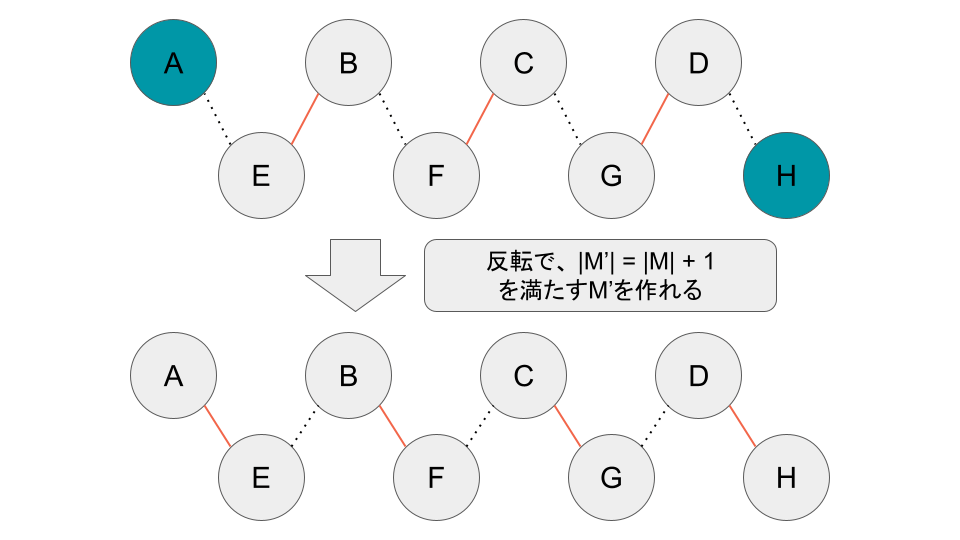
この図上側のグラフにおいて、A-E-B-F-C-G-D-Hが増加道です。確かに増加道の出発点(A)と到着点(H)はマッチングの部分グラフに含まれないので、マッチングの端点ではないですし(緑で塗りつぶしたノード)、マッチングに含まれているエッジと含まれていないエッジが交互になっています。この交互になっている道の、マッチングと非マッチングエッジを反転させることで、$|M'| = |M| + 1$なる$M'$を見つけることができます。

補足説明

マッチング$M$について、「増加道が存在しない $\Leftrightarrow$ $M$は最大マッチング」をそれぞれ補足説明^[20]します。

増加道が存在しない $\Leftarrow$ Mは最大マッチング

この対偶は、「増加道が存在すれば最大マッチングではない」となり、上の図から明らかですので、この命題は成立します。

増加道が存在しない $\Rightarrow$ Mは最大マッチング

こちらも対偶「最大マッチングではないなら、増加道が存在する」を考えて、これを確認していきます。

最大マッチングでないマッチングを$M$、真の最大マッチングを$M'$とします（$|M'|>|M|$）。

$M$のエッジと$M'$のエッジの対称差^[21]であるエッジ集合を$M\Delta M'$とします。1ノードが2つ以上のエッジを持たないというマッチングの性質より、一つのノードに隣接している$M\Delta M'$のエッジは二本以下なので、$M\Delta M'$は道(A-E-B-F)と、長さが偶数の閉路^[22](C-D-H-G)とに分けられます。

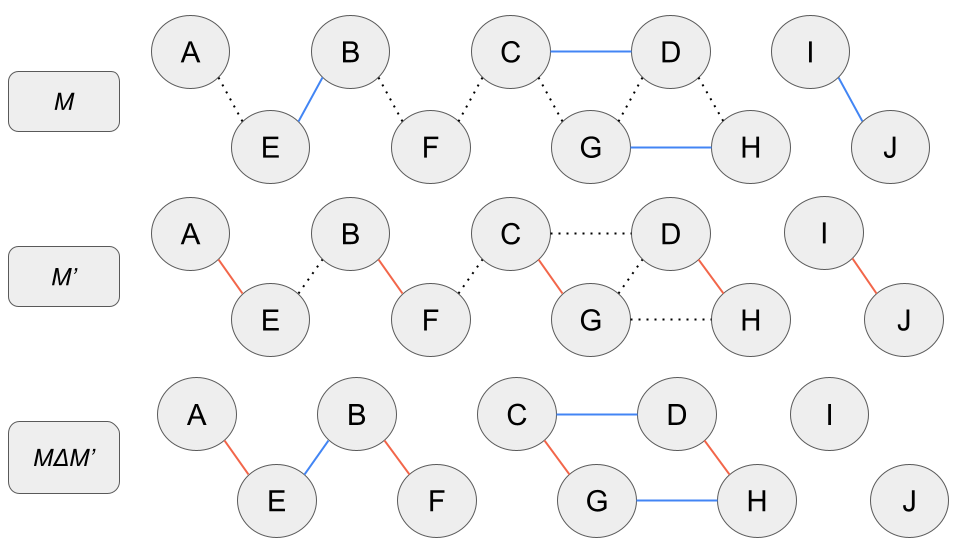
対称差の例。マッチング$M, M'$の対称差は、$M$と$M'$のどちらかで使われていてかつ、共通して使われていないエッジの集合で表されます。I-J間のエッジは共通して使われているため、対称差からは除かれます。

道のマッチングペア数:

$M$のエッジと$M'$のエッジが交互に登場することと、$|M'|>|M|$であることから、$|M'|=|M|+1$

長さ偶数の閉路のマッチングペア数：

$M$のエッジ(青色)と$M'$のエッジ(オレンジ色)が交互に登場（同じ色が連続していたらマッチングとしておかしい）するので、$|M|$=$|M'|$

以上の議論から、長さ偶数の閉路（図の例ではC-D-H-G)ではマッチングペア数は変わりません。道の方では、$M'$のエッジからはじまり$M'$のエッジで終わる増加道(図の例ではA-E-B-F)が存在し、この増加道中のマッチングで使っているエッジとマッチングで使われていないエッジのマッチング状況を反転させれば、全体としてマッチングペア数を+1することができます。

線形計画法への適用

今回の線形計画法の目的関数は、$\sum_{i}\sum_{j} w_{i,j} x_{i,j} + \lambda \sum_{i}\sum_{j}x_{i,j}$ でしたね。基本的には第一項でエッジ重み和が大きくなるように、第二項はマッチングペア数が多くなるようにする効果が期待されます。ここで、第一項が大きくなるよりも、優先的に第二項の方がが大きくなるような$\lambda$が存在すれば最大マッチングが実現できます。

グラフ理論に基づく最大マッチングアルゴリズムでは、

1. 増加道を見つける
2. 増加道中のマッチング状況を反転させる

を増加道が見つからなくなるまで繰り返す素朴な方法が用いられています。線形計画法で置き換えるのであれば、増加道が見つかった時に、それを反転させた時、必ず目的関数の値が増加するように$\lambda$を設計すれば良いです。なので、増加道が見つかった時に(最大マッチングではない状態から、サイズ$|M|$が1大きくなる時の目的関数の各項の動き方を確認していきます。

第一項$\sum_{i}\sum_{j} w_{i,j} x_{i,j}$

最大マッチングではない状態$M$から、ペア数が1増多い$M'$になる際、最も大きい増え幅を考えます。

• $M$のときに、第一項が取りうる下界
• $M'$のときに、第一項が取りうる上界

をそれぞれ計算し、差を計算すればよいですね^[23]。$M$のときの下界は、思い切って0としましょう。マッチング重み行列$W$の各要素が$>0$さえ保証すれば良いです。

次に$M'$における上界を考えます。$\sum W$と$\sum X$のそれぞれの最大値を掛け合わせた$N \times \max(W)$ が第一項の取りうる上界です。
以上から、第一項の最大変化量は

$$N \times \max(W) - 0$$

となります。

第二項$\lambda \sum_{i}\sum_{j}x_{i,j}$

これは単純にマッチングが1つ増えているので、$\sum X$は2増えるので、マッチング数$M$の状態Aから、マッチング数$(M+1)$の次の状態になると、第二項は$2\lambda$増えます。

よって、第二項の最大変化量は

$$2\lambda$$

です。

第一項と第二項の差に着目

第一項の最大変化量と第二項の最大変化量
$2 \lambda > N \times \max(W)$であれば、どんな状況でもマッチング数が多い方が、目的関数値が大きくなるように$\lambda$を設計できます。よって例えば、

$$\lambda = N \times \max(W)$$

にしておけば安全に最大マッチング条件を満たせます。

線形計画法による最大マッチングの実装

線形計画法によるエッジ重み和が最大となる最大マッチング実装は、Pythonの数理最適化ライブラリpulpを用いれば簡単に実現できます。以下にサンプルコードを記載します。

from typing import Any

import numpy as np
import pulp

N = 1000
W: np.ndarray[float, Any]  # マッチング重み行列
X: np.ndarray[int, Any]  # マッチング行列
ng_pair_list: list[list[int]]  # マッチングさせないペアのリスト
problem = pulp.LpProblem("matching", pulp.LpMaximize)

# 目的関数 maximize(ΣWX + λΣX)
lambda_ = N * np.max(W)  # 頂点数N
problem += pulp.lpDot(W, X) + lambda_ * pulp.lpSum(X)

# 制約条件
for i in range(N):
    # 1人以下としかマッチングできない
    problem += pulp.lpSum(X[i, :]) <= 1
    problem += pulp.lpSum(X[:, i]) <= 1

    # 自分自身とはマッチングできない
    problem += X[i, i] == 0

    # 対称性（iとjがマッチングしていたらjとiもマッチングしている）
    for j in range(i):
        problem += X[i, j] == X[j, i]


# NGペアをマッチングさせない制約条件を追加
for ng_pair in ng_pair_list:
    ng_idx1 = ng_pair[0]
    ng_idx2 = ng_pair[1]
    # ng_pairは絶対にマッチングしないように0にする
    problem += X[ng_idx1, ng_idx2] == 0  # 行列の対称性はbase_restrictで制約済

problem.solve(pulp.PULP_CBC_CMD(timeLimit=60))  # CPU時間が60秒で制限

結び

本記事ではENTASのベータ版リリースに併せて、マッチングアルゴリズムを紹介しました。数理最適化では、想定外の最適化が行われ、実態に即さない結果を返してしまうことがあります（今回の例ですと、最大マッチングになっていないときなどです）。こういったことが起きないように、あらゆるパターンでソフトウェアテストをすることも大切ですが、理論的にはっきりしている部分は理論的に起きないように工夫するべきと考えています。今回はまさに、最大マッチングであることが保証できると、自分の中で確信しながら業務に取り組むことができました。

今まで何件かTechブログとして記事を書いてきましたが、業務に関わるものはなかなか外に出しにくく、いずれも業務とは無関係なものでした。本記事の執筆を通じ、自分の仕事内容を外部に発信できることはとても楽しい・嬉しいことだと再認識できました。それも読み手あってのことと存じます。ここまで読んでくださった皆様にはとても感謝しております。ありがとうございました。

ENTASのリリースはもちろん、マッチングアルゴリズムだけでは到底実現できません。ビジネス、デザイナ、開発、チーム一丸で作り上げました。ENTASプロジェクトの最初に「良いマッチングとは何か」をプロジェクトメンバーみんなで議論したのが印象深かったです。これからも新機能の追加等、開発を進めてまいりますので、ENTASをどうぞ、よろしくお願いいたします。

参考文献

• 福島雅夫. 新版 数理計画入門. 朝倉書店, 2013.

お知らせ

少しでも弊社にご興味を持っていただけた方は、お気軽にご連絡頂けますと幸いです。まずはカジュアルにお話を、という形でも、副業を検討したいという形でも歓迎しています。

https://recruit.zenkigen.co.jp/career
https://speakerdeck.com/zenkigenforrecruit/detailed-version-recruitment-materials-for-data-scientists

脚注

1. 執筆執筆当時

2. TMS(誰が何を知っているかを知っている状態。1人ではなく、チームでさまざまな情報に対応できること)の向上を目指しています。

3. AさんとCさんはマッチングNGという意味合いでNG条件という表現を用いています。

4. 一般のグラフではない例としては、2部グラフが有名です。これは男女でペアを作る、道路と車を割り当てる、といった状況です。

5. 「大企業」には明確な定義はありませんが、厚生労働省等が出す資料では、1000人以上の従業員がいる会社を大企業と分類することが多いようです。

6. 実際上はマッチングの計算を始めて、翌朝くらいに計算が終わっていれば十分なのですが、何事も早く終わることに越したことはありません。

7. 必ず線形オーダーというわけではありませんが、経験的に$O(N)$で実現できることが知られています。詳細は参考文献 新版 数理計画入門をご参照ください。

8. シャッフルトークという性質上、必ずしも最も良いマッチングである必要はなく、準最適解でも全く問題ありません。

9. 「エッジ重み和が最大となる最大マッチング」のような表現は、以後何度も出てきますが、「最大」という文字が2回続き、読みにくくて恐縮です。注意してお読みください。

10. グラフ中の任意の2ノード間にエッジが存在するグラフを完全グラフと言います。

11. 後述しますが、エッジ重みは全て0より大きくなるように作ります。

12. 待遇をとれば明らかですが、最大マッチングではないとき、NG条件がないので余った2人をペアにすればエッジ重み和を増やすことができるので、エッジ重み和が最大なはずがありません。

13. 理由は図で示した反例で十分ですよね。

14. これは、$i$さんから見た$j$さんとマッチングしたときの嬉しさと、$j$さんから見た$i$さんとマッチングした時の嬉しさが等しいことを意味します(グラフの言葉では無向グラフに相当します)。これは、単に$i$さんと$j$さんが過去にマッチングしたことがあるかどうかや、普段から会話が多いかどうかの所属条件によってマッチング時の嬉しさが決まるとしているため、$i$さんが$j$さんに片想いしているというような状況は考えていません。

15. 制約条件に記載していますが、$i = j$のときは必ず0とします。

16. $V$がノード集合、$E$がエッジ集合です。

17. https://dl.acm.org/doi/pdf/10.1145/6462.6502 Theorem 1 より。

18. 単にエッジで繋がったノード列のことです。

19. 増加道についてはこちらの記事を読むと理解の助けになるかもしれません。

20. 厳密な証明は大変なので雰囲気を理解していただければと思います。

21. 集合$A$と集合$B$の対称差$A\Delta B$とは、$A$には属するが$B$には属さない$A \setminus B$の要素と、$B$には属するが$A$には属さない$B \setminus A$の要素からなる集合$(A \setminus B) \cup (B \setminus A)$を意味します。

22. ループがあるグラフのことです。

23. 厳密に最小値、最大値を計算して差をとっても良いですが、大雑把な評価で十分ですね。ペア数が1増えるので、一見シンプルに$2 \times \max(W)$と思えるかもしれませんが、1ペア増えるだけではなく、他のペア組み合わせも変わる可能性があるので、$2 \times \max(W)$ではダメです。