時計を用いないサウナ滞在時間推定法の検討と実践

はじめに

初めまして。ZENKIGENデータサイエンスチーム所属のredteaです。原籍はオムロンソーシアルソリューションズ株式会社 技術創造センタ^[1]ですが、社外出向でZENKIGENに所属しており、数理最適化や機械学習を用いたデータの分析業務をしております。今回が初執筆で張り切っています！

いきなりですが、先日私がサウナに行った時の話をさせてください。
最近はサウナを趣味にしている人が周りに増え始め、遅ればせながら私も「整って」^[2]みたいと思い、サウナに行くことにしました。サウナ初心者の私は、「整う」ための方法を事前にインターネットで調べ、例えばサウナ浴を5~10分→水風呂を30秒→休憩5分 のルーティンを何回か繰り返す必要があることを知りました。

下調べを終え意気揚々とサウナに行ったところ、サウナは非常に高温ですので、普通のメガネをしたままサウナに入ることができないことをその場で知りました‼︎サウナ室には確かにそこそこの大きさの時計がおいてはあったのですが、私の裸眼では文字盤を認識することができず、慣れない高温下でどれほどの時間を過ごしているのか全く検討がつかない状況になってしまいました。これではもちろん「整う」ことはできませんでした。

どうにか、視力が悪い人でもサウナ内でおおよその時間を測定する方法はないかと、80 ${}^\circ$C の室内で思考を巡らせた結果、

他のサウナー^[3]の方々は時計を見ながら整うための時間を計ってサウナから退室しているとするなら、退室した人数を数えることで、統計学的に時間を推定できないだろうか。

と考えました。

本記事では、統計学の知識とPythonによるシミュレーションから時間推定法を検討し、実際にサウナで実践した結果を報告します。

サウナについて

サウナの入り方

公益社団法人日本サウナ・スパ協会で紹介されている方法を参考に、サウナの入り方を以下のようにまとめました。

1. 服を全て脱ぐ（メガネ・腕時計等も全て外す）
2. シャワーを頭から浴び、全身をよく洗う
3. サウナに8~12分滞在する^[4]
4. 水で汗をしっかり流す
5. 水風呂に30秒〜1分入る
6. 5分ほど休憩する
7. 3に戻って6までを3~4回繰り返す

サウナの入り方を実践するにあたっての問題点

サウナ室の中には時計は置いてありますが、裸眼視力が悪い人はサウナ内で時間を計ることができません。サウナでも使えるメガネなど、代用品は既に市販されていますが

• できれば身体には何も付けずに過ごしたい
• まだ初心者でサウナのためだけに何かを買うのに抵抗がある

といった方々には、もっと簡単に時間を知る方法が望まれていると考えています。

用語の整理

本記事で扱う用語を以下にまとめました。入室・退室というと、サウナに入ったり出たりすることを表します。また、サウナ室に滞在することと、水風呂や休憩などを含めてサウナ浴と言ったりする場合があるので、それらとは明確に区別するために、高温のサウナ室にいることを「滞在」と定義します。

語句	意味
入室	サウナ室に入ること
退室	サウナ室を出ること
滞在	高温のサウナ室内にいること
滞在時間	高温のサウナ室内に滞在する時間
滞在人数	サウナ室内にいる人の数

時間推定方法(統計学による理論)

統計学の復習

この節では、本記事で用いる統計学の知識を簡単に紹介します。また、サウナ滞在時間においてどのような使われ方をするかについても触れます。
内容は統計学入門, 日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブックを参照して書きました。

ポアソン分布

ポアソン分布は、「ある期間に平均 $\lambda$ 回起こる事象が、ある期間に $X$ 回起こる回数の分布」を表します。まさに、ある期間(=1分間)に $\lambda$ 人の人がサウナに入室する状況を表すのにピッタリな確率分布です。

$$P(X=x) = \frac{\lambda^x e^{- \lambda}}{x!}$$

指数分布

指数分布は、「ある期間に平均して $1 / \mu$ 回起こる事象が起こってから、次に起こるまでの期間 $X$ の分布」を表します。言い換えると、平均的に $\mu$ という期間に1回起こる事象が起こる時間間隔の分布です。サウナの例では、人が入室してから退室するまでの時間分布に相当します。平均的に8分程度で退室すると仮定すれば、$\mu=8$ となります( $\mu > 0$ )。

$$P(X=x) = \begin{cases} \frac{1}{\mu} e^{-x / \mu} & (x \ge 0) \\ 0 & (x < 0) \end{cases}$$

ガンマ分布

ガンマ分布は、指数分布の一般化です。「ある期間に平均して $1/\beta$ 回起こる事象が、$\alpha$ 回起こるまでの時間 $X$ の分布」を表します。例えば自分が8分間を計りたいとした時に、パラメータ $\beta$ を推定(仮定)した上で、サウナから退室する人数が $\alpha$ 人になる時のガンマ分布の期待値が8になるような $\alpha$ を決めれば、本記事のゴールです。

また、確率分布が得られるので、サウナ室内で $\alpha$ 人数えた時の経過時間の信頼区間を求めることができ、どの程度の精度で時間を推定できるかまで分かります。

ガンマ分布の確率密度関数の定義は以下の通りです。

$$P(X=x) = \begin{cases} \frac{1}{\beta^\alpha \Gamma(\alpha)} x^{\alpha - 1}e^{-\frac{x}{\beta}} & (x \ge 0) \\ 0 & (x < 0) \end{cases}$$

ここで、$\Gamma(\alpha)$ が次に示すガンマ関数を表します。

$$\Gamma(\alpha) = \int_0^\infin x^{\alpha - 1}e^{-x} dx \qquad \alpha > 0$$

• 1分間に2人が退室するとして($1/\beta=2$)、16人退室する($\alpha=16$)までに経過する時間の分布
• 1分間に4人が退室するとして($1/\beta=4$)、32人退室する($\alpha=32$)までに経過する時間の分布

を以下に描きました。

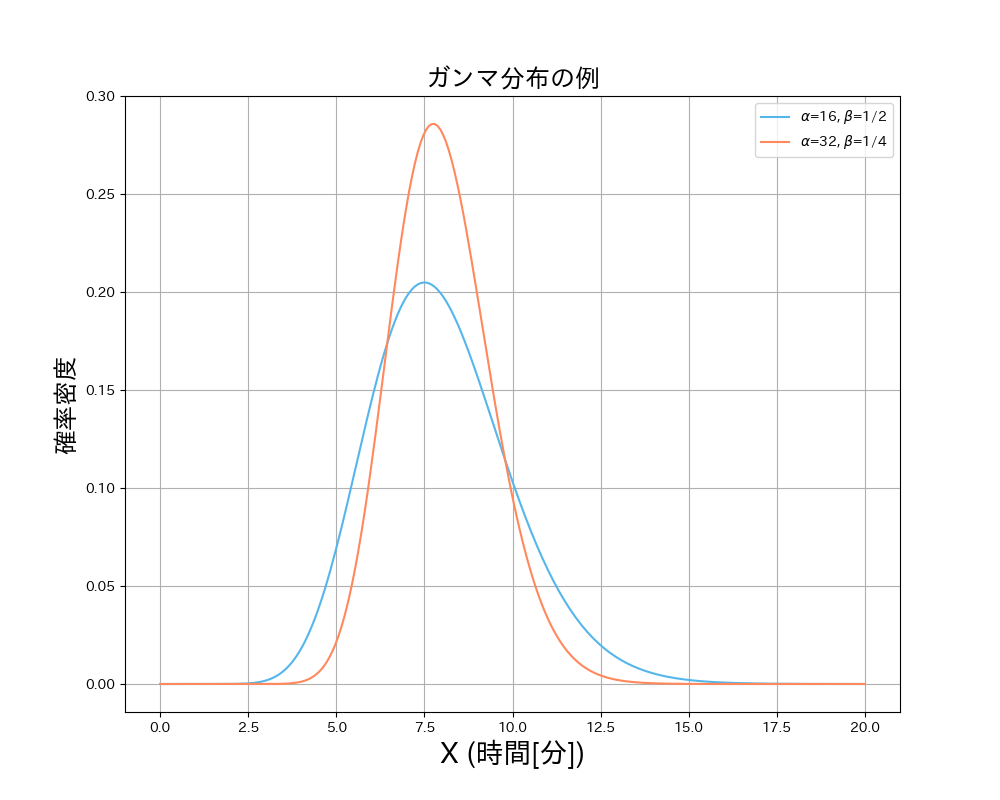
ガンマ分布の確率密度関数の例
青線の方は「平均的に1/2分に1人退室するとき、16人退室するまでの人数を数えた時の経過時間の分布」を、
オレンジ線の方は「平均的に1/4分に1人退室するとき、32人退室するまでの人数を数えた時の経過時間の分布」を表します。

ガンマ分布の期待値と分散はそれぞれ、

$$E(X)=\alpha \beta \\ V(X) = \alpha \beta^2$$

ですので、このパラメータ設定では、どちらも期待値が8分近くになっており、分散は

• 青: $16 \times (1/2)^2 = 4$
• オレンジ: $32 \times (1/4)^2 = 2$

となるので、オレンジの線の方が分散が小さくなっています。

問題の設定

統計学的に解析可能な問題とするために、以下の仮定を起きます^[5]。

• 1分間の入室人数は、パラメータ $\lambda$ のポアソン分布に従う。
• 各人の入室から退室までの時間は、パラメータ $\mu$ の指数分布に従う。
• 入室過程と退室過程は独立(「たくさん入室してきたから退室しよう」といったことは起こらない)。
• 入退室において、無記憶性を仮定する(将来の入退室は過去の入退室に依存しない。言い換えれば、「誰かが出たから自分も出よう」といったことは起こらない^[6])。
• サウナ室は十分に広く、サウナ内の人数が多すぎて入るのを断念する人はいない^[7]。
• サウナ営業の開店から十分時間が経過し、サウナの滞在人数は定常状態になっている。
• 定常状態においては、
  • 定常状態における滞在人数の平均値は、自分が入室した時のサウナ内人数$N$と一致する。
  • 1分間あたりの退室人数が一定(= $1 / \beta$ )で、退室はランダムに発生する。
  • よって、$\alpha$ 人が退室するまでの時間分布はパラメータ $\alpha, \beta$ のガンマ分布に従う。

実はこの問題設定は、レジなどの「待ち行列」という有名な問題と近しいです。今回のポイントは、レジの数が無限であるところと、関心ごとがレジで会計を終える人がどのような分布で発生するか、です。

サウナ滞在時間推定における各分布のパラメータの決定

本節では、指数分布のパラメータ $\mu$、 ポアソン分布のパラメータ $\lambda$、ガンマ分布のパラメータ $\alpha, \beta$、を定めていきます。

• $\mu$: 退室時間の期待値は、サウナで推奨の8分と仮定する( $\mu=8$ )
• $\lambda$: $\lambda$ は直接観測できないので^[8]、以下の通り推定する
  1. 自分が入室する時の滞在人数 $N$ を数える(仮定より、これは定常状態の滞在人数と一致する)。
  2. ある十分な期間$T$における合計入室人数の期待値は、$\lambda T$ 人
  3. ある十分な期間$T$における合計退室人数の期待値は、$NT / \mu$ 人
  4. 定常状態である仮定から、ある時刻において入退室する人数は釣り合っているので、$\lambda T = NT/\mu$
  5. よって、$\lambda = N/\mu = N/8$
• $\beta$: 定常状態においては、入室者数の期待値は同じであるから、$1/\beta = \lambda = N/\mu$
• $\alpha$: サウナ内で$\tau$分計測したいとすると
  • ガンマ分布の期待値 $\alpha \beta$ が $\tau$ と一致させたいので、
  • $\alpha = \tau / \beta = \tau N / \mu$

時間推定法

前節で確率分布のパラメータが決まったためあとは簡単です。手順を以下に示しますので、使ってみたい方はこの方法をお試しください！

1. 自分がサウナ内に滞在したい時間 $\tau$ 分を決める(例えば$\tau=5$分)。
2. 今回訪れたサウナ施設の客層から、他の人は平均 $\mu$ 分程度滞在するかの見立てを立てる(例えば$\mu=8$分)。
3. サウナに入室したら、サウナ内滞在人数$N$を数える(例えば$N=20$人)。
4. ガンマ分布のパラメータ $\alpha = \tau N / \mu$ を暗算する(今回の例では$5\times20\div8=12.5$)。
5. $\alpha=12.5$ 人退室するまでサウナ室内で滞在する。

$\mu=8$ 分, $N=20$ 人とした時、 「$\tau$ 分滞在したいので、$\alpha$ 人数えた時」に経過する時間の分布は以下の通りです。

自分がサウナ室内に滞在したい時間$\tau$分の時に、この理論を実践した時の滞在時間の分布

また、滞在したい時間の$\pm2$分以内に退室できる割合を以下の表にまとめています^[9]。

滞在したい時間($\tau$ 分)	数える人数 $\alpha$ 人	$\beta$	$\tau-2$ 分未満になる割合	$\tau+2$ 分以上になる割合	$\pm2$分以内に収まる割合
5	12.5	0.4	5.86%	8.82%	85.4%
8	20	0.4	12.5%	13.4%	74.1%
12	30	0.4	18.2%	17.7%	64.1%

滞在したい時間が5分のように短い場合は、ほとんどが$\pm2$分以内に収まります。一方、12分滞在しようとすると、自分の滞在時間が10~14分になる割合は64.1%であり、信頼性が低くなってしまいます。滞在したい時間が長くなるほど、$\pm2$ 分以内の範囲に収まる割合は小さくなるのは、長時間計測すればそれだけ誤差が大きくなることを表しており、直感に反しない結果となりました。

Pythonによるシミュレーション

シミュレーションの目的

問題の設定の節にて、サウナ室内で数えるべき人数を $\alpha = \tau N / \mu$ と決定することができたものの、多数の仮定をおいていました。実際は、サウナ利用客全員の滞在時間の指数分布パラメータが一定の $\mu$ とは限りませんし、退室時間の分布もガンマ分布に従うことを証明したわけでもありません。可能な限り厳密に行うためには、以下の項目の対応が必要ではないかと考えています。

• 前章では、$\alpha$ 人退室するまでの時間はガンマ分布に従うとしたが、人を個別に見ると、もっと厳密に計算する必要がある。
  • 各サウナ利用客はそれぞれ独立なパラメータ $\mu_i$ の指数分布$X_i$に従い退室する。
  • $X_i$ を小さい順に並べた時の初めの $\alpha$ 人が退室する時間の分布を考える必要がある^[10]。
  • 自分が入室した時点で既にサウナに滞在している人達の、入室から今までの滞在時間の分布も考慮する必要がある。
• 自分が入室した時のサウナ内滞在人数が、定常状態のサウナ内滞在人数と一致しているという仮定は、多くの場合で成り立たない。

これらの要素を考慮すると解析的に解くのが難しくなるため、前章では少々強めの仮定をおいて計算していました。本章では、可能な限り現実に近い状況でシミュレーションを行い、多数の仮定をおいて算出した理論値と比較することで、前章での仮定が適切であったかどうかを検証していきます。

シミュレーション結果のサマリー

まずはシミュレーション結果を先にお見せします。詳細は次の節からです。

• 退室人数を数えることで、自分の滞在時間はほぼガンマ分布に従った。
• 以下の図は自分が $\tau=5$ 分滞在したいときの滞在時間の分布であり、定性的にガンマ分布のようになっていることが確認できる。
• シミュレーションによるサウナ内滞在時間の平均値はガンマ分布による理論値よりも少し短めになり、分散は小さめな結果となった。

本記事の時間推定法に従い、退室人数を数えて退室した時の滞在時間の分布(自分が5分滞在したい時)

シミュレーション設定

本シミュレーションでは、計算が困難なためにおいていた仮定を可能な限り減らすことで、より現実に近い状況をシミュレーションすることを目指します。
シミュレーションでおく仮定と、理論でおいた仮定の違いは以下の通りです(表中の$N$は、今までと同様「定常状態の滞在人数の期待値」を表す)。

項目	理論計算時の仮定	シミュレーションでの仮定	補足
自分の入室時の滞在人数	必ず $N$ 人	仮定なし	この仮定は強すぎるので仮定しない方が自然
サウナに入室する人数の分布	$N$ 人が滞在していることを前提に $\lambda = N / \mu$のポアソン分布	観測できないパラメータ $\lambda$ のポアソン分布	-
他の人のサウナ滞在時間の分布	全員同じパラメータ$\mu$の指数分布	$i$ さんは $\mu_i$ のパタメータを持つ($\mu_i$ の分布は仮定する)	-
サウナ室を人が退室する時間間隔の分布	ガンマ分布に従う	仮定しない	仮定しなくとも理論的に計算すればガンマ分布かもしれない
自分が入室した時の滞在者が過去滞在していた時間	考慮しない	考慮する	実際の状況を再現することで考慮する

サウナ滞在時間を扱った問題なので、時間の単位は「分」で良さそうですが、連続型分布である指数分布を扱うため、本シミュレーションは微小時間を秒で捉えて、1秒単位のシミュレーションを行います^[11]。可視化や集計をする際に、適宜分単位に直します。計算量の工夫を一切しておりませんので、シミュレーションは3分程度かかります。では、シミュレーションプログラムを見ていきましょう(プログラムを信じてくださる方は読み飛ばしてOKです)！

シミュレーションプログラム(Python)

全ソースコードはGitHubにおいております。パラメータなどを変えて実行したい方は是非ご利用ください。本節では、一部抜粋して説明します。なお、ソースコードは更新し、本記事は修正しない可能性がありますので、GitHub上のコードと、本記事に記載しているコードが異なる場合がございます。ご了承ください。

https://github.com/atsushi-green/sauna_simulation/tree/main

step1. 自分以外の人の動き(入退室)をシミュレーション

まずはポアソン分布に従って人を入室させる処理です。

1秒ごとに、この judge_enter_sauna_with_poisson() 関数が呼ばれます。np.random.rand() は0以上1未満の一様乱数なので、1分間で平均 lambda_ 回 True が返る(60回この関数が呼び出されると、平均的に lambda_ 回 True が返る)ようになっています。これがまさにポアソン分布の正体です。

def judge_enter_sauna_with_poisson(lambda_: float) -> bool:
    """ポアソン分布に従って、ある微小時間(1秒)にサウナへの入室者がいるかどうかを判定
    ポアソン分布では、微小時間に2回以上事象が発生することはないことを仮定している。

    Args:
        lambda_ (float): ポアソン分布のパラメータλ(人/分)

    Returns:
        bool: この微小時間に人が入ってくるならTrue, そうでないならFalse
    """
    return np.random.rand() < (lambda_ / 60)

---

次に1人がある瞬間(秒)に入室した時、その人が退室する時間を決めてしまいます。

calc_exit_time_with_exp() 関数によって、平均$\mu$分の指数分布に従う値(秒)を返しています。
コメントアウトしている u = calc_exit_time_with_exp(ASSUMED_MU) を採用すると、サウナに来る人全員が同じ指数分布のパラメータ $\mu$ を持つことになります。今回の実装では、あらかじめ設定したパラメータ MU_DISTRIBUTION の分布に従ってランダムに選ばれるようになっています。

def main():
    (中略)
    # ■ step1-1. 自分以外の人の動きを(入退室)をシミュレーション
    for el_sec in range(MAX_SIMULATION_SECONDS):
        # 1周1秒のforループシミュレーション
        if judge_enter_sauna_with_poisson(LAMBDA):  # ポアソン分布でこの1秒間に入室があったかどうか判定
            enter_count_list[el_sec] += 1
            # 今入った人の滞在時間は、パラメータmuの指数分布に従う
            mu = random.choice(MU_DISTRIBUTION)
            # そして今入った人は、u秒後にサウナを退室する(uを指数分布で決める)
            u = calc_exit_time_with_exp(mu)
            # u = calc_exit_time_with_exp(ASSUMED_MU)  # こっちはより仮定が強い

def calc_exit_time_with_exp(mu: float) -> int:
    """指数分布に従い、サウナを退室するまでの時間を決める

    Args:
        mu (float): 指数分布のパラメータμ(分/回)

    Returns:
        int: 何秒後にサウナを退室するか
    """
    # 簡単のために、round(偶数丸め)で整数に丸める
    return round(np.random.exponential(scale=mu * 60, size=None))

step2. 自分が入室した時の振る舞いをシミュレーション

各瞬間(el_sec 秒)に入室した時の、滞在人数を数えて、数えるべき人数 $\alpha$ を計算し、実際に退室人数が $\alpha$ 人を超えるまでに経過する時間を記録しています。

理論の方では、自分がサウナに入室した時の滞在人数は必ず定常状態の滞在人数の期待値$N$であることを仮定していました。コメントアウトしてある n = N の方を採用すると、この理論通りの設定になります。今回の実装では、シミュレーション上での入室時の人数を用いています。

COUNT_ENTER_EXIT_FLG が True の時の挙動は、本記事の最後の方に出てくる入室人数も数える場合の実装ですので、ここでは気にせず、False だと思って読んでください。

def main():
    (中略)
    # ■　step2-1. 自分が入室してから、中の人を数えて、退室するまでの時間をシミュレーション
    # サウナに行く前に、自分が滞在したい時間τを決める
    result_dict: Dict[int, List[int]] = {tau: [] for tau in TAU_LSIT}
    for tau in TAU_LSIT:
        for el_sec in tqdm(range(MAX_SIMULATION_SECONDS)):
            # el_sec: 自分がサウナに入った時刻(秒)
            n = num_in_sauna_list[el_sec]  # 自分が入室した時、まずはサウナ室内の人数を数えてnを得る
            # n = N  # こっちは自分が入室する時は必ず定常状態の期待値の人数がサウナに滞在していると仮定

            # ガンマ分布のパラメータαを計算し、α人退室するまでに経過する時間(my_stay_sec)を計算する
            if COUNT_ENTER_EXIT_FLG:
                alpha = 2 * tau * n / ASSUMED_MU
                my_stay_sec = calc_my_stay_sec(el_sec, alpha, exit_count_list, enter_count_list)
            else:
                alpha = tau * n / ASSUMED_MU
                my_stay_sec = calc_my_stay_sec(el_sec, alpha, exit_count_list)

            # もし自分がサウナに入ってから退室するまでにα人数え終わらなかったら、実験結果から除く
            if my_stay_sec is not None:
                result_dict[tau].append(my_stay_sec // 60)

シミュレーション結果の確認

では結果を見ていきましょう。このプログラムを実行すると、7つの図が出力されます。出力される図のファイル名は、

• 01.1分あたりの入室人数の分布.png
• 02.1分あたりの退室人数の分布.png
• 03.サウナ室内滞在人数の変遷_4時間.png
• 03.サウナ室内滞在人数の変遷_24時間.png
• 04.自分が入室してから退室するまでの時間の分布(分)(τ=5).png
• 04.自分が入室してから退室するまでの時間の分布(分)(τ=8).png
• 04.自分が入室してから退室するまでの時間の分布(分)(τ=12).png

です。

入退室人数の分布

まずは入退室人数の分布です。図を見ると、両方とも理論通りのポアソン分布に従っていそうです。

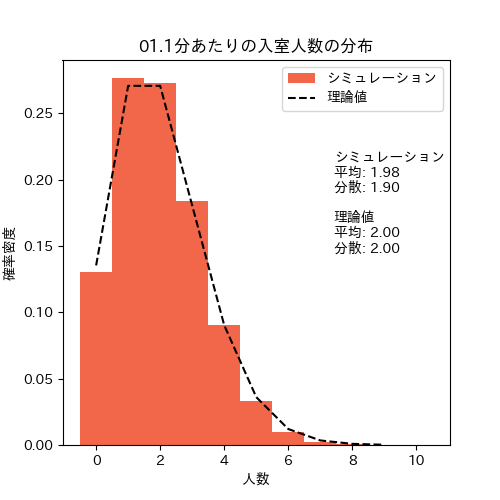
1分間の入室人数の分布

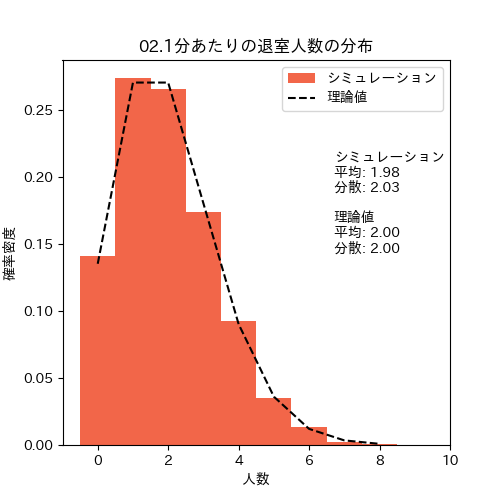
1分間の退室人数の分布

シミュレーション上では、入室人数は本当は観測できないパラメータ $\lambda$ のポアソン分布に従い、それらの人が指数分布に従って滞在するとしていますが、退室人数の分布は仮定していないにも関わらず、退室人数もポアソン分布に従ってくれました。私はできませんでしたが、数学の計算がしっかりできれば、退室人数の分布もポアソン分布であることを導けるのでしょうね。

サウナ室の定常状態の確認

サウナ室内の様子も気になりますので、1分ごとのサウナ室内人数の推移をプロットしてみました。まずは24時間分です。

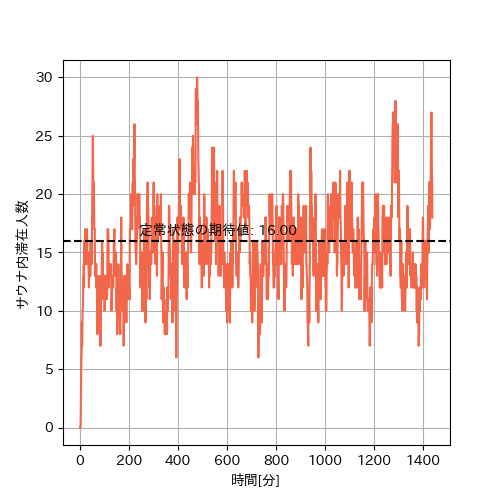
サウナ室内人数の推移(24時間分）

定常状態の期待値である16付近で、6~30くらいの間で人数推移しているように見えますね。このことから、十分な時間が経過すればサウナ室内は定常状態になることもわかりました。この図だけではどれくらいの時間で定常状態になるか見にくいので、最初の4時間だけ拡大してみてみます。

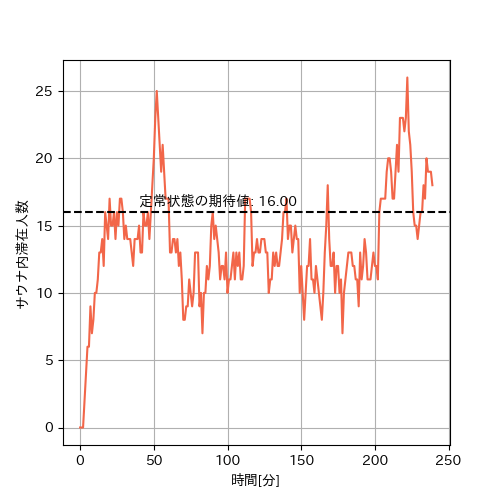
サウナ室内人数の推移(4時間分）

定性的ではありますが、図から30分も経てば定常状態になっていることを確認できます。従って、サウナ営業開始から(またはサウナ内のタオル交換などでリセットが起こってから)30分程度経てばこの理論を使って問題なさそうなことがわかりました。

自分のサウナ室内滞在時間の確認

いよいよ本題です。自分が$\tau=5,8,12$分 滞在したい時の滞在時間の平均と分散はおよそ理論値と一致しています。ただ、どの$\tau$においても滞在時間が短くななり、分散も小さくなっているようにも見えます。

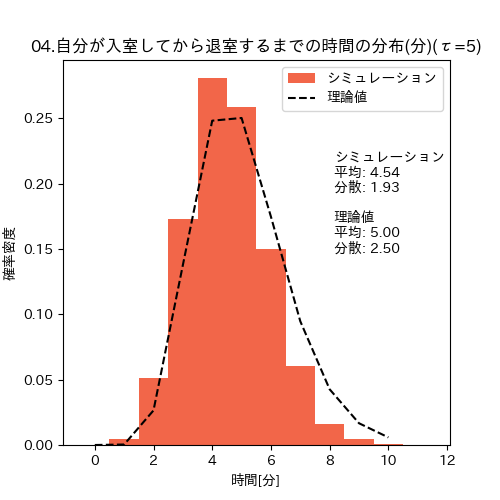
今回の理論に従って退室人数を数えて退室した時の滞在時間の分布(自分が5分滞在したい時)

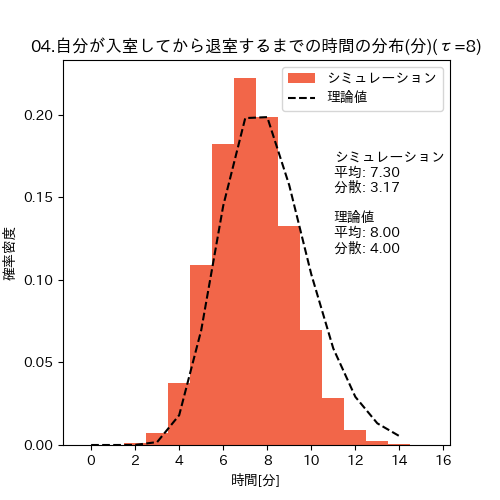
今回の理論に従って退室人数を数えて退室した時の滞在時間の分布(自分が8分滞在したい時)

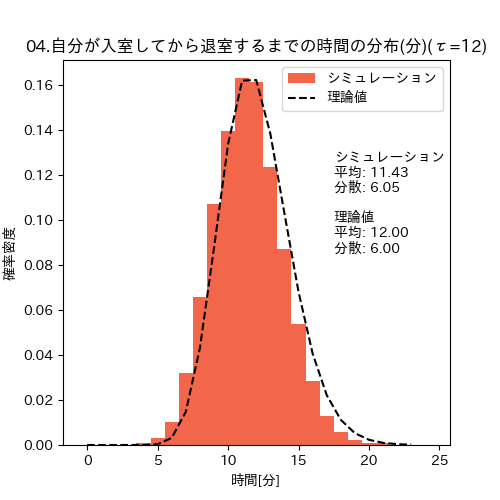
今回の理論に従って退室人数を数えて退室した時の滞在時間の分布(自分が12分滞在したい時)

この乖離の原因は、理論で計算した時においた仮定をシミュレーション上ではおいていないことによる差異と考えています。他の可能性としては、シミュレーションによる誤差や実装上の問題が含まれている可能性もありますが、シミュレーション内での時間で1万分(166時間)回しているのでシミュレーション誤差はほとんどないはずで^[12]、シミュレーションが正しいとき、実際にサウナでこの方法を試すと、想定より10%程度早く退室してしまう可能性があります。

=====自分がtau=5分滞在したいときの実際の滞在時間=====
ガンマ分布理論値: 平均=5.000, 分散=2.500
シミュレーション: 平均=4.538, 分散=1.935

=====自分がtau=8分滞在したいときの実際の滞在時間=====
ガンマ分布理論値: 平均=8.000, 分散=4.000
シミュレーション: 平均=7.301, 分散=3.169

=====自分がtau=12分滞在したいときの実際の滞在時間=====
ガンマ分布理論値: 平均=12.000, 分散=6.000
シミュレーション: 平均=11.426, 分散=6.049

サウナでの実践(実証実験)

実践環境

ついに「整いリベンジ」の日がやってきました。2023年6月某日、統計学の知識($\alpha=\tau N/\mu$)とシミュレーション結果を頭に入れ、首都圏にある人気サウナ施設で上記の時間推定方法を実践しました。この時私はサウナに行くのが2回目の初心者でしたので、サウナ室内滞在時間は$\tau=5$分と決めました。また、訪れたのはサウナ専用施設ではなく、日帰り温泉施設なのでサウナ目的の人ばかりではないことから、他の人の滞在時間の平均値は一般的な$\mu=8$分と決めました。$\tau=5$分, $\mu=8$分なので、退室人数カウント $\alpha = \tau N/ \mu = 5N/8$ ですね(室内人数を数えて5倍し、8で割る)。

先のシミュレーションでは少し早めに退室してしまうので、ゆっくりめに退室する作戦もあり得ましたが、今回の実践はシンプルに行うため、理論値をそのまま用いることにしています。

なお、入室する直前にサウナ室外にある大きな時計で時間を確認し、退室直後に再度時間を確認することで滞在時間を実測しました。では、結果を見ていきましょう。

実践結果

結果

私のサウナ耐性の都合で、サウナ滞在→水風呂→休憩のループは3周が限界でした^[13]。結果は以下の表のとおりです。

	入った時の滞在人数 $n$ 人	数えるべき人数 $\alpha$	滞在時間(分)	誤差
1周目	25	15.6	7	+2分
2周目	9	5.62	4	NA
3周目	18	11.25	6	+1分

2周目は、3人数えた段階でタオル交換^[14]のため強制中断を余儀なくされました。ガンマ分布を仮定した時、3人数えた時の待ち時間の期待値は、$\alpha \beta= 3 \times \mu/N = 3\times8 / 9 = 2.67$分なので、一応これも$\pm2$分以内に収まったことにしています。
1、3周目は$\pm2$分以内に収まっており、実践としては満足な結果でした。

考察・感想

シミュレーションでは、滞在時間がガンマ分布の理論値よりも短くなるという結果が得られていましたが、実践では逆に長く滞在する傾向になりました。原因は、

• 想定した他のサウナー達の平均滞在時間 $\mu$ が実は8分よりもっと長かった
• 実践回数が3周で少ないため、偶然偏った結果が得られた
• 理論やシミュレーションで仮定していたことの一部が、実際には成り立たないものが含まれていた

など、いろいろ考えられますが、これらの要因を特定するのは非常に難しく、もう少しサウナに通いながら分析を進めていきたいと思います。サウナ室内で使えるメガネでも買って、時計を見ながら入退室の様子を観測すれば、より良い方法が思いつきそうです^[15]。

さらなる精度向上に向けて

3回の実践ではあるものの、現時点でもそこそこの精度で推定することができます。しかし、より「整いやすく」するには精度が高いに越したことはありません。精度を高める1つのアイデアは

退室人数だけでなく、入室人数も数えることで、分散を小さくできないだろうか

です。

理論

基本的な考え方は、

• シミュレーション結果から、入室人数も退室人数もポアソン分布に従っている
• ポアソン分布には再生性^[16]という性質がある
• 入室人数と退室人数は独立と仮定できる（「人がたくさん入ってきたから出よう」は考えない）

最後の仮定は、入室人数と退室人数の期待値が等しくなる(定常状態)ことと矛盾するので、かなり怪しい仮定となっていますが、一旦は無視して議論を進めます。

この状況から、ある十分な期間 $T$ における合計入退室人数の期待値は $\lambda T + NT / \mu$ 人です。また、入退室人数の期待値は一致することから、$\lambda T = NT / \mu$　を用いて、 $\lambda = N / \mu$ だったので、入退室人数の期待値は$2 \lambda$です。

(入室or退室)をイベントだと考えた時のガンマ分布のパラメータ $1/\beta=2\lambda, \alpha=\tau/\beta=2\tau N / \mu$ と計算できます。パラメータだけ見ると、退室人数に加えて入室人数も数えるので、合計数える人数が2倍になり、$\beta$ が小さくなるので分散が小さくなることが期待できそうです。

実は本記事の「統計学の復習」のガンマ分布紹介時の図で、入退室人数を数えた場合にばらつきが抑えられる様子を描画していました。青線が退室人数のみを数えた場合で、オレンジ線が入退室人数を数えた場合です。滞在時間の期待値はもちろんどちらも同じですが、分散はそれぞれ4, 2なので、精度を高められていることがわかります。以下に図を再掲します。

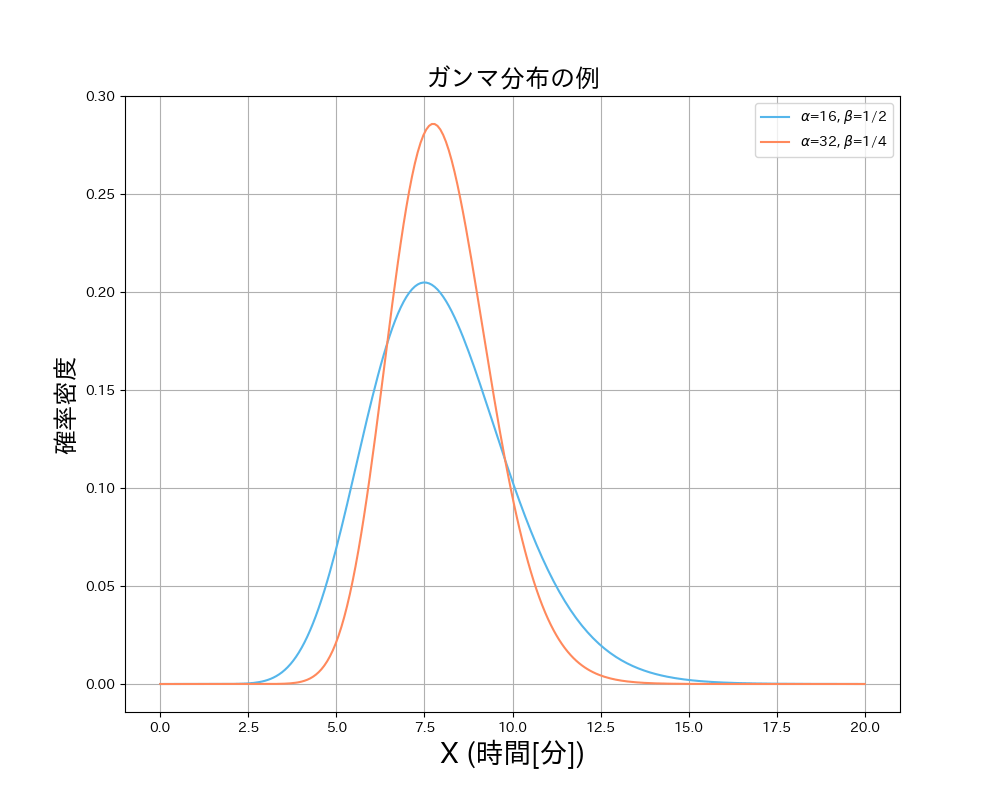
ガンマ分布の確率密度関数の例
青線の方は「平均的に1/2分に1人退室するとき、16人退室するまでの人数を数えた時の経過時間の分布」を(すなわち退室人数のみを数える場合)、
オレンジ線の方は「平均的に1/4分に1人退室するとき、32人退室するまでの人数を数えた時の経過時間の分布」を表します(すなわち入退室人数を数える場合)。

シミュレーション

先のシミュレーションプログラムのCOUNT_ENTER_EXIT_FLG を True にすれば、入室人数も数えた場合のシミュレーションができます。実行結果は以下の図の通り、シミュレーションの方の分散が小さくならず、期待したような精度向上は見られませんでした。この原因は、

入室人数と退室人数は独立と仮定できる（「人がたくさん入ってきたから出よう」は考えない）

という仮定が成立しないことが原因と考えています。実際、ランダムに入ってくる入室者が偶然多いタイミングでは、それだけ退室する人数も増えてしまうので、独立というわけにはいかないようです。

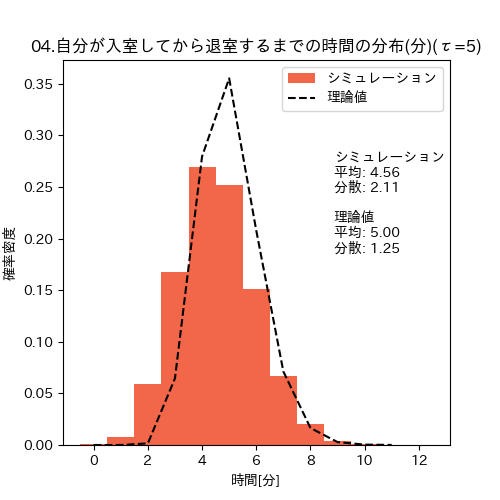
入退室人数を数えて退室した時の滞在時間の分布(自分が5分滞在したい時)

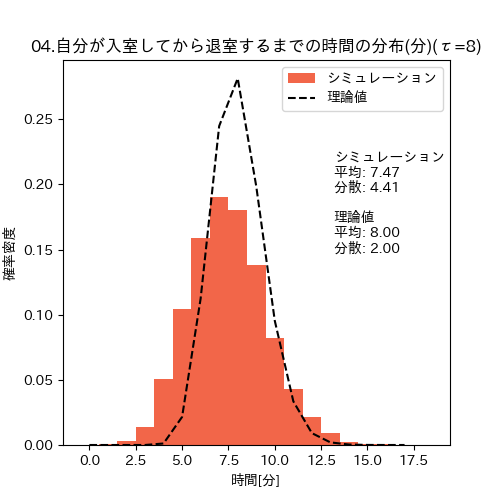
入退室人数を数えて退室した時の滞在時間の分布(自分が8分滞在したい時)

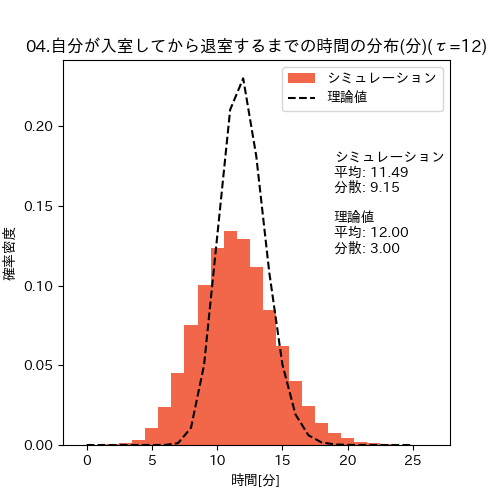
入退室人数を数えて退室した時の滞在時間の分布(自分が12分滞在したい時)

シミュレーション結果から、残念ながら単純に入室人数を足すだけでは精度向上できないことがわかりました。

結び

本記事では、サウナ室内ではメガネがかけられず時間がわからないという問題から、退室人数を数えることで時間が推定できないか検討しました。その結果、$\tau$ 分を計るには、このサウナ施設の利用者の平均サウナ滞在時間 $\mu$ を仮定し、入室時のサウナ滞在人数$N$を数え、他の人が $\alpha=\tau N/\mu$ 人退室してから自分が退室すれば良いことがわかりました。実際のサウナ施設で実践した結果、$\pm2$ 分以内の誤差でサウナ室に滞在することはできたものの、私自身はまだ「整った」実感は得られていません。これからもこの方法を用いて時間を計り、「整える」ようサウナに通ってみようと思います。皆様も是非、この方法をお試しあれ。 ただし、ご自身の身体がしんどくなってきたら退室人数を数えるのを諦めて、サッと退室しましょう。

シミュレーションを通じて、より現実に近い設定でも、多くの仮説をおいた理論通りの結果が得られました。残念ながら現状ではより精度を上げる方法が思いついておりませんが、サウナに通う中でアイデアが閃けば記事にしたいと思います。

サウナも記事執筆も初心者の身^[17]で拙くなってしまいましたが、本記事を一部でも読んでいただければ嬉しい限りです。本記事を執筆するにあたり、多数の助言をくださったZENKIGEN、オムロンソーシアルソリューションズのチームの方、ZENKIGENサウナ部の方に感謝申し上げます。

参考文献

• 東京大学教養学部統計学教室, 統計学入門[基礎統計学], 東京大学出版会, 1991.
• 一般社団法人 日本統計学会, 日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック学術図書出版社, 2020.
• 公益社団法人日本サウナ・スパ協会, 20223年6月9日閲覧, https://www.sauna.or.jp/jigyou/jigyou.html

お知らせ

少しでも弊社にご興味を持っていただけた方は、お気軽にご連絡頂けますと幸いです。まずはカジュアルにお話を、という形でも、副業を検討したいという形でも歓迎しています。

https://recruit.zenkigen.co.jp/career
https://speakerdeck.com/zenkigenforrecruit/detailed-version-recruitment-materials-for-data-scientists

脚注

1. 原籍では主に鉄道や道路のデータ分析を担当していました。

2. 脳内でリラックスと興奮が同時に生じて快感を得られる状態のことです。

3. サウナをこよなく愛する人達のことです。

4. サウナの滞在時間は個人差があり、閲覧するホームページごとに推奨時間が異なりますが、ここではこの記事を基準にします。

5. まさか計算機や筆記用具を持ち込めないサウナ室内で、定積分など複雑な計算はできないので、最終的な時間推定式はシンプルなものになるよう心がけます。

6. この記事の内容をみんなが実践するとこの仮定が成り立たなくなります。皮肉なものですね。

7. もしサウナ内の人数が多すぎるような条件下では、そもそも人数 $N$ を数えるのが難しいので考えないようにします。

8. サウナの外から時計を持って人数を数えるのは時間がかかる上、不審者になってしまいます。

9. 詳細は割愛ですが、各条件におけるガンマ分布のパラメータ $\alpha, \beta$を求め、$\tau - 2$ 分未満になる割合は、ガンマ分布の下側累積確率を算出し、$\tau + 2$ 分以上になる割合は1-{ガンマ分布の下側累積確率}で求めました。

10. このように、確率変数の中で最も小さいものや大きいものの性質を扱う概念を極値統計と呼ぶようです。

11. ポアソン分布は微小時間に2回以上事象が発生しないことを前提としている確率分布なので、1秒に2人以上入室することはないことはポアソン分布を使う上で大前提です。

12. 現状、実装の正しさは信じていただくしかないですが、ご指摘はお待ちしております！よろしくお願いします！

13. 3周目の途中では、早く$\alpha$人退室ないかなぁってずっと思いながら滞在していました。皆さんも絶対に無理のない範囲で実践してくださいね。

14. サウナ室内の座るところにはタオルが敷いてあるのですが、時間が経つと汗まみれになるので、スタッフさんが定期的にタオルを交換してくれます。タオル交換時には作業の都合上、一旦サウナ滞在者は全員外に出ることになります。

15. 本末転倒ですね。

16. ポアソン分布の再生性とは、 $X_1 \sim \text{poisson}(\lambda_1), X_2 \sim \text{poisson}(\lambda_2)$であり、$X_1$ と $X_2$ が独立の時、$X_1 + X_2 \sim \text{poisson}(\lambda_1 + \lambda_2)$が成立する性質のことです。

17. 今回が初執筆です。