🧊

NeRF-RPN：NeRF上で物体検出する技術

はまなすなぎさ

2023/04/13に公開

はじめに

こんにちは。ZENKIGEN DSチームに所属しているはまなすです。DeNA AI技術開発部より^[1]、業務委託という形で主に深層学習系の開発に携わっています。

今回は、ニューラルネットワークを用いて3次元空間を表現する NeRF という技術に基づいた、立体空間内で物体検出をおこなう手法 NeRF-RPN についてご紹介します。

https://arxiv.org/abs/2211.11646

本研究は昨年末に発表されたものですが、今のところ実験結果が限定的であるため、直ちに実応用に展開されているわけではありません。一方で、今回ご紹介するような『NeRFの上に積み重なる手法』は、NeRFを活用する土壌をさらに拡大させる一翼を担っていくことが期待されます。

近年は表現技術としてのNeRFそれ自体の発展が目覚ましいですが、NeRF-RPN は、その上で『なにをするか』を充実させるためのひとつの基礎研究となるでしょう。

▼ NeRF-RPN はなにをした研究？

Fig.1. NeRF-RPN：NeRF上での物体検出例。最も確信度の高い12領域を可視化。NeRFはINRIAの生活空間シーンにおいて訓練された。NeRF-RPN: A general framework for object detection in NeRFs より引用。

NeRF-RPN の初出は2022年11月下旬です。本研究ではその名の通り、『NeRF』で構成された立体空間において、画像における既存の物体検出モジュールである『RPN』を拡張して導入することを提案しました。概要をまとめると、本研究の貢献は以下のようになります。

★ NeRF上で直接動作する物体検出手法としての、世界初の取り組み

これまでも点群やRGBD画像、あるいは複数視点のRGB画像を用いた3次元物体検出手法は提案されてきました。一方で、これらの多くはボクセル表現への落とし込みがもたらす高いメモリ消費や、限られた参照画像視点数に依拠する精度劣化に課題を抱えていました。

提案手法では、NeRFによる空間表現をそのまま活用し、NeRFをいかなる視点からもレンダリングすることなく、空間内の物体の3次元矩形領域を直接回帰推定できることを実証しています。これにより、NeRFにより獲得された連続的な潜在表現を効果的に反映した、高精度な物体検出が実現されました。

ただし、NeRF-RPN では物体を囲む領域を検出する手法を提案するに留まっており、現行で発展している画像内物体検出のように、物体ラベルを分類するところまでは至っていないことには留意が必要です。その意味でも、今後のマイルストーン的な側面が強い研究といえるでしょう。

★ 3次元物体認識のためのデータセット構築

本研究では新規な課題を設定しているため、提案手法を適切に評価できる既存データセットが存在しない点にも留意が必要です。

そこで本研究では、室内シーンに関する合成データセットである Hypersim と 3D-FRONT、および実世界の室内シーンデータセットである ScanNet と SceneNN を組み合わせ、NeRF の学習とその中での物体検出に適した大規模ベンチマークを構築しました。

さて、ここまでで NeRF-RPN の概要をざっくり把握しました。ここからは、もう少し具体的に手法を深掘りして理解したい方向けに記事を綴っていきたいと思います。

まず、背景として NeRF と RPN についておさらいしていきましょう。いずれも既に有用な解説記事は数多く存在しているので、以下では簡潔な紹介に留めます。その後、NeRF-RPN 本体の論文解説に移るという流れで進行します。

▼ NeRF（Neural Radiance Fields）

NeRF では、ある特定の3次元シーンを任意角度で眺めた視点を表現できるよう、シーンを多角的に撮影した複数画像をもとにニューラルネットワークを訓練します。空間内の任意座標 $(x,y,z)$ が、あるカメラ角度 $(\theta,\phi)$ から見たときに何色 $(r,g,b)$ に見えるかを、密度（その点における不透明度） $\sigma$ を含む連続的な輝度場として表すことでこれを実現します。学習するモデルを $F_\Theta$ と表すと、NeRFやその派生研究に共通する入出力フォーマットは次のようになります：

F_\Theta:(x,y,z,\theta,\phi) \to (r,g,b,\sigma).

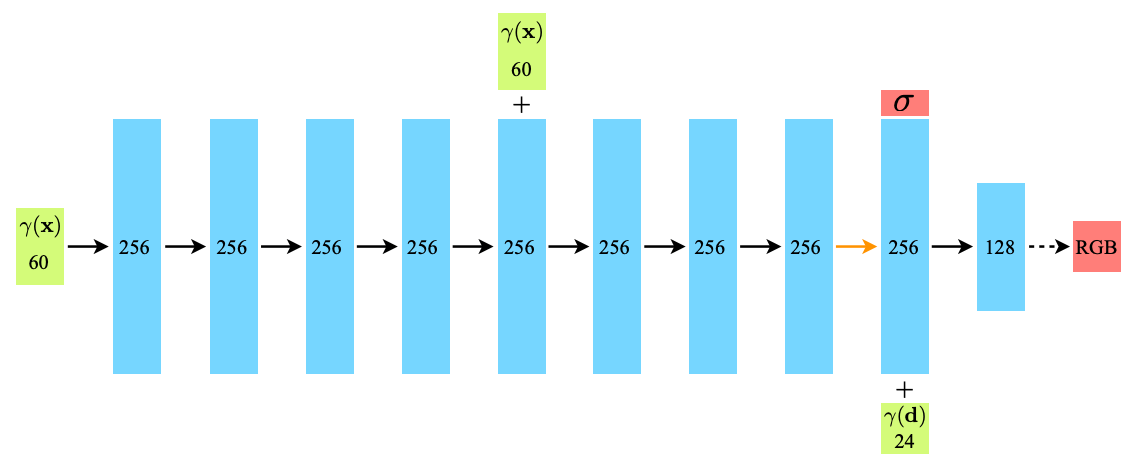
入出力が高々数個の変数であることもあり、 $F_\Theta$ としては、256次元程度の線形層を積層した比較的軽量なネットワークが用いられました。

Fig.2. NeRFの $F_\Theta$ 。図中の変数について、 $\bm{x}=(x,y,z), \bm{d}=(\theta,\phi)$ 。 $\gamma$ は位置符号化関数。黒矢印は線形層とReLU、黒点矢印は線形層とシグモイド関数、橙矢印は活性化関数を伴わない線形層。『+』は特徴ベクトルの結合。密度推定がカメラの角度に非依存となるよう、 $\sigma$ を出力するまでは $\bm{d}$ が入力されない構造となっている。NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis より引用。

その上で、NeRFではボリュームレンダリングという積分計算をおこない、対象シーンを任意視点で見た際の各画素値を獲得します。Fig.3 では目のマークから赤い矢印が伸び、その線上に点が複数並んでいると思いますが、このようにある視線上の点をサンプリングしてスクリーン上に最終的に映る色を計算するわけですね。この計算は微分可能なので、深層学習に自然に組み込めます。

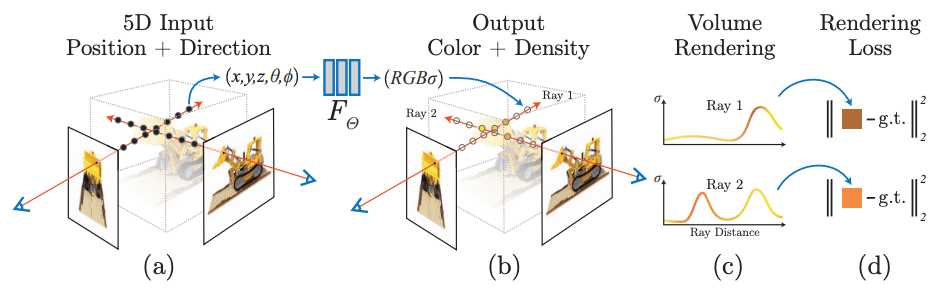
Fig.3. NeRFの概要。(a) (b) ではモデルの入出力、(c)ではボリュームレンダリングの概要、(d)では各視点でのボリュームレンダリング結果をもとに入力画像との誤差を計算して訓練することが示されている。NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis より引用。

これが訓練画像とそのカメラ角度において一致するようにモデルを学習させることで、最終的にモデル内部に一貫性を持った空間表現が獲得され、入力画像にはない任意角度からシーンを見た際の視点をも整合性をもって描画できるようになります。

こうして学習されたモデルの出力としてどのような結果が得られるのかは、オリジナルの研究に際して著者らが公開した動画を閲覧すると、非常に直感的に理解することができます。

NeRF の主な貢献は、ニューラルネットワークの表現力を高精細で破綻の少ない空間表現に上手く活用したこと、およびそれを実現するために微分可能で効率的な学習フレームワークを提案したことにあるといえるでしょう。

一方で、通常の深層学習的な観念からは誤解しやすい NeRF の特徴として、『あらゆるシーンを表現可能な汎用モデルを学習するわけではなく、ある単一シーンの表現に特化したモデルを獲得する技術である』ということには留意する必要があります。つまり、ある特定のシーンに紐づく既知の画像群が学習データで、同じシーンの未知の任意視点が全て評価データということですね。

その他、オリジナルのNeRFにおける制限としては、『対象シーンが静的でなければならない（動きや照明の変化は考慮されていない）こと』『同一シーンの画像が100枚単位で必要なこと』『ひとつのシーンを学習するために NVIDIA V100 GPU 1枚で約1~2日要すること』が挙げられます。

他に、入力が合成シーンでない場合は『各視点の画像におけるカメラパラメータが既知でなければならない』点も制限となり得ますが、NeRF では COLMAP SfM package を利用することで実画像群におけるカメラパラメータを推定し、この問題を回避しています。

NeRF の派生手法

前節のNeRFの強みを活かしつつ、弱点を克服するための研究として、様々な後続手法が提案され続けています。例えば NeRF-W（NeRF in the Wild）では、あるシーンが様々な天候や照明条件、あるいは一時的な物体や人物が写った状態で撮影され、静的とはいえないその多様な画像群が入手できるという、より現実的な設定のもとでNeRFを学習する手法を考案しています。

また NSFF（Neural Scene Flow Fields）では、単一の動画を時刻情報を含む複数視点画像群と捉えてシーンを再構成し、時空間的に滑らかなNeRF表現を獲得する手法が提案されました。

さらに、NeRF の学習に必要な画像視点数を大幅に削減する工夫も提案されています。pixelNeRF では、数枚（極端には1枚）の画像から NeRF の学習が可能です。十分な枚数で学習した NeRF と比較するとぼやけた印象の生成品質ではありますが、通常の NeRF では学習が破綻するような小規模データで学習できるのは特筆に値します（特に 4:40 付近からの比較）。

NeRFの頑健性や表現力を拡張するだけでなく、学習や推論時間を高速化するような手法も盛んに研究されています。2022年初旬に提案された Instant NeRF では、多段解像度のハッシュ符号化やCUDAカーネルの最適化といった工夫を盛り込むことにより、さながらインスタントカメラを携行するかの如き軽快さで NeRF が学習可能になりました。ハイパーパラメータによって品質と訓練時間のトレードオフを調整することもできるため、RTX 3090 程度の性能を持つ GPU ならば、数秒から数十秒で NeRF を学習し、60FPSで描画することも可能であると述べられています。

2023年2月下旬には、メモリ効率を大幅に改善した MERF が提案されました。デモ動画からは VRAM が約200MB程度であることや、Macbook Pro M1 で30FPS以上、RTX 3090 で60FPS以上で動作する様子が確認でき、従来手法よりも省メモリかつ高速であることが伺えます。

驚くべきことに、ちょうど同時期、iPhone端末上で NeRF による高画質3Dキャプチャアプリを展開する Luma AI より、当該アプリのモデルアップデートがアナウンスされました。端末上の処理で30FPSの描画を実現する軽量化により、エッジデバイス上での NeRF 活用がさらに身近なものとなっていくことが期待されます。

さらに2023年4月初旬には、次世代ゲームエンジンである Unreal Engine 5 上でリアルタイム動作する NeRF プラグインが公開され、NeRF がより一般に触れられやすい土壌が拡大しています。

NeRF の表現特性を拡張するような研究も盛んです。2023年の CVPR に採択された ${\rm F}^2$ -NeRF では、透視ワーピングという手法を考案することにより、対象空間に境界があることを暗に仮定せず、任意のカメラ軌跡から NeRF を学習できます。生成品質も高く、学習も数分程度のようです。

また、2023年の ICLR に採択された PAC-NeRF では、複数視点の動画から幾何形状だけでなく弾性のような物理特性を再現するなど、NeRF の表現力をさらに次の舞台へ引き上げています。
https://sites.google.com/view/PAC-NeRF

加えて、こうした発展はText2Imageのような近年の生成AIの発展とも結びつき、テキストからの3次元物体生成として Latent-NeRF や Magic3D といった手法へも繋がっていきました。この文脈では、特に最近、全方位から見た際の整合性を大幅に向上させる DITTO-NeRF が登場しています。
https://janeyeon.github.io/ditto-nerf/

同様に、画像編集手法の InstructPix2Pix に着想を得て、プロンプトによる指示ベースで NeRF のテクスチャやジオメトリを変換する Instruct 3D-to-3D といった手法への発展を見せたりもしています（余談：ちなみにこの研究の主著者は筆者の研究室時代の同期だったりします）。

NeRF は単なる技術的な面白さだけでなく、現実のランドマークの仮想空間上への再現・保存や、自在なカメラワークを活かしたゲーム・エンタメ領域への展開等、多岐にわたって既に応用されており、これからもますます応用されていくでしょう。その潜在的な可用性や発展性における懐の広さも、NeRF を魅力的な技術たらしめる要因といえそうです。

▼ RPN（Region Proposal Network）

さて、話は一転して、今回のもうひとつの要である RPN について触れたいと思います。RPN は画像に対する物体検出器の内部モジュールで、なにかしらの物体が映っていそうな領域を抽出する仕組みです。初出は Faster R-CNN と呼ばれる物体検出手法で、以降多くの亜種が登場しています。

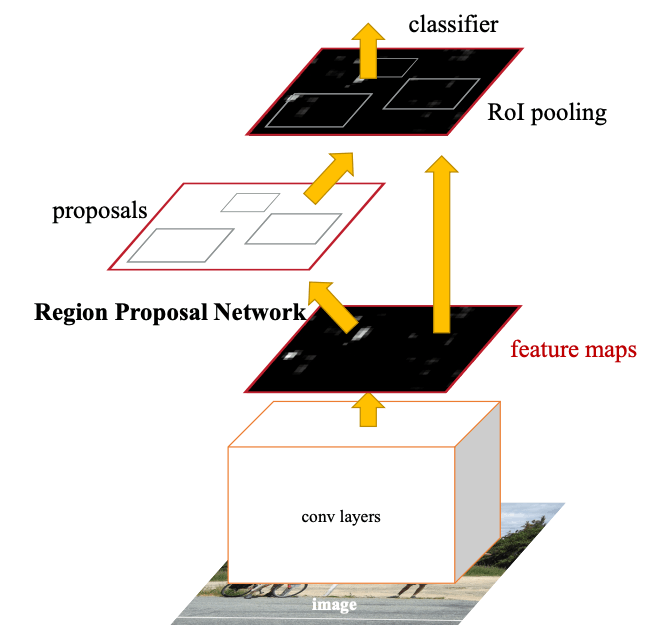
Fig.4. Faster R-CNNの概要。入力画像をCNNバックボーンに通して得られた特徴マップに基づき、RPNにて領域を提案。提案された矩形領域内の特徴マップをROIプーリングという処理で規格化したのち、写っている物体を分類器で予測する。Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks より引用。

（のちにアンカーベースとして分類される当初の）RPN は、複数種類の矩形候補の位置やサイズを回帰推定しつつ、矩形内に物体が存在する尤度を最大化するよう学習されるCNNモデルです。ニューラルネットワークで構成された RPN により End2End（入力から出力まで微分勾配が途切れない状態で一気通貫）にモデル全体を学習できるようになり、選択的探索法などの高負荷なヒューリスティック手法を用いていた従来手法と比べ、処理効率や検出精度が大きく改善されました。

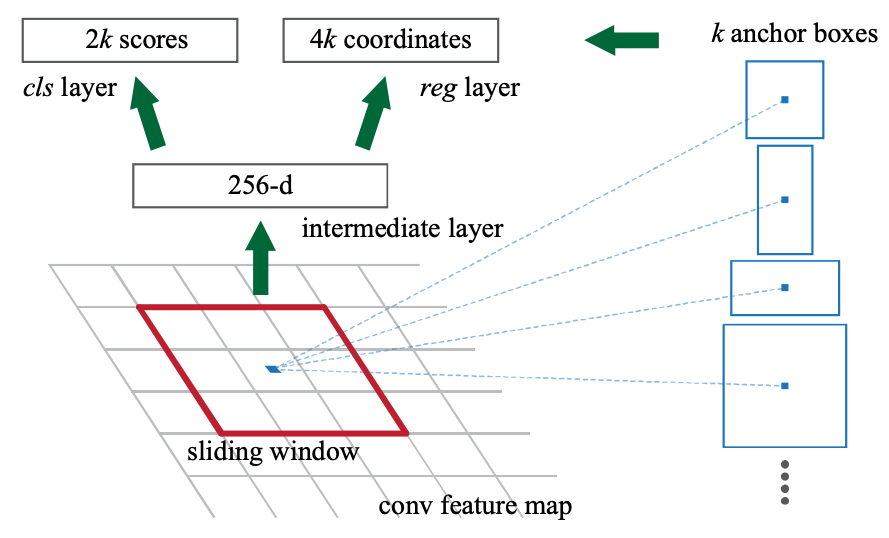
Fig.5. RPNの概要。入力画像をCNNバックボーンに通して得られた特徴マップにの各ピクセルにおいて、適切な矩形領域と物体の存在確率を学習する。Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks より引用。

Faster R-CNN で提案されたオリジナルの RPN は、まず入力画像を VGG16 等のCNNバックボーンに通して低解像度化された特徴マップを受け取ります。その各ピクセルを中心点として、予め設定した基準長と縦横比を組み合わせて作った矩形領域候補群を仮想的に照会し（Fig.5 赤枠）、各枠において物体が存在しそうな確率を推定します。

ところで、このようにテンプレート的に用意した矩形領域をそのまま用いると、元の入力画像において最終出力される物体領域はかなり粗いものになってしまうため、より精緻な矩形領域を提案する仕組みがあると望ましいです。RPN ではここにも手が届いており、物体の存在確率が一定以上と判断された候補領域について、さらに領域を微調整する変数を予測します。具体的には、矩形領域の中心座標の誤差、および領域の高さと幅の誤差を回帰推定するよう学習されます。

こうして得られた提案領域を用いて、Fig.4 に示すように特徴マップをくり抜き、最終的な物体検出の予測に用います。ここでくり抜かれる矩形領域は、RoI（Region of Interest：関心領域）プーリングと呼ばれる工夫により、元の提案領域の形に関わらず、固定サイズの特徴量として抽出されます。これによって、後段の物体クラスの予測等を共通のモジュールでおこなえるわけですね。

Faster R-CNN ではCNNバックボーンのある中間層のみを利用しますが、後続研究では、複数解像度の中間特徴をピラミッドのように用いることで矩形領域のサイズに幅を持たせる FPN なども登場し、より大域的な領域や、反対に非常に小さな領域における検出性能も向上しました。他に、矩形領域を回転させた領域も検出できる Oriented R-CNN のような派生手法も存在します。

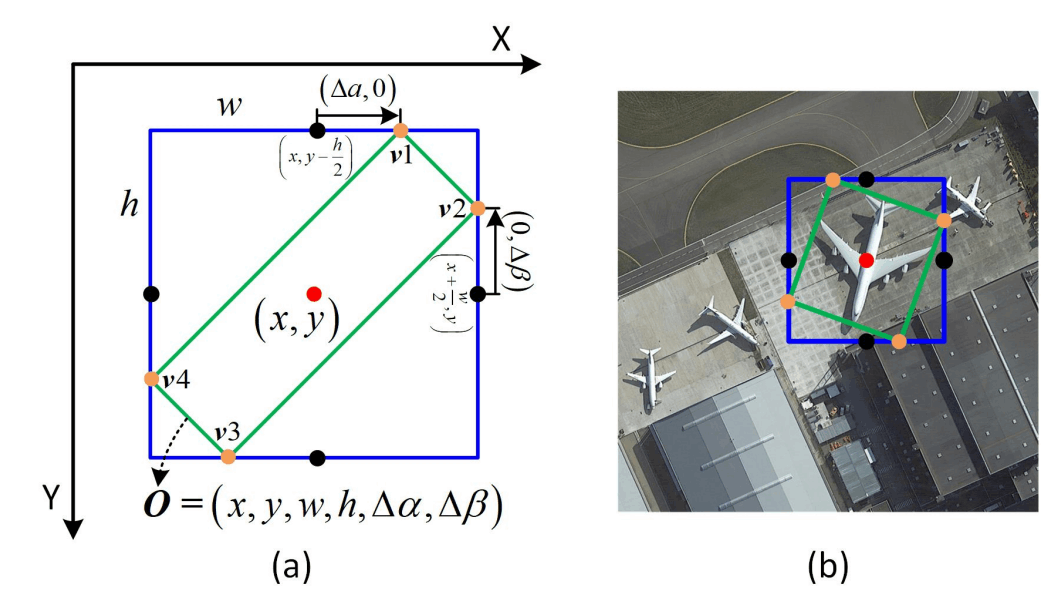
Fig.6. Oriented R-CNN による回転矩形領域の検出例。Oriented R-CNN for Object Detection より引用。

Faster R-CNN で提案された RPN のように、初めに複数の矩形領域候補を当てはめる手法はアンカーベース手法とも呼ばれます。対照的に、矩形領域とその物体存在確率を直接一気に予測する FCOS のような手法も提案されており、こちらはアンカーフリー手法と呼ばれます。

▼ NeRF-RPN

ここまでの話を組み合わせれば、NeRF-RPN の出来上がりです。詳細には、3次元空間を表現する NeRF において RPN を適用できるよう、空間方向への拡張などの工夫が施されています。以下ではこれを見ていきましょう。

アーキテクチャ

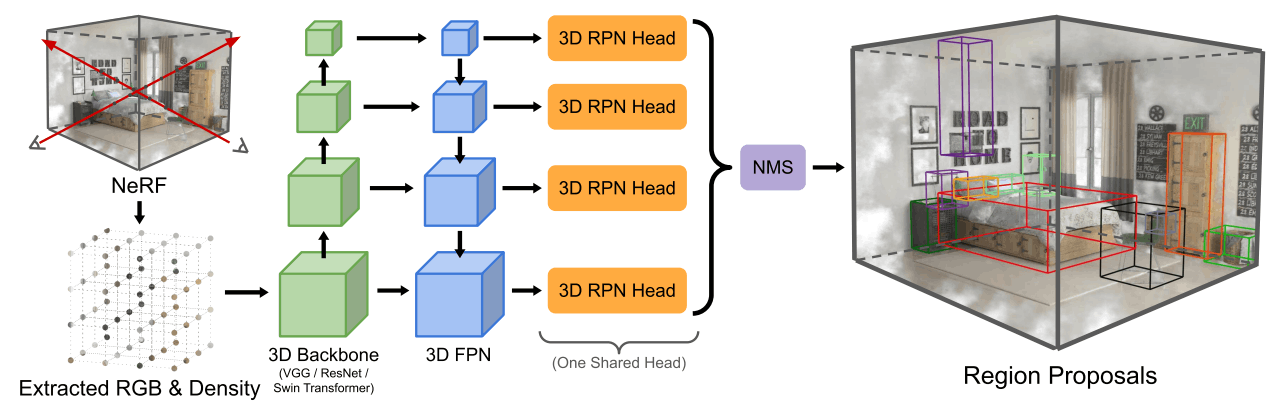
Fig.7. NeRF-RPNの概要。与えられた NeRF を3次元的にサンプリングしたのち、3D CNNから成るバックボーンネットワークにより階層的に特徴抽出。3次元拡張した RPN で領域提案し、物体検出をおこなう。NeRF-RPN: A general framework for object detection in NeRFs より引用。

NeRF-RPN では、あるシーンの学習済み NeRF を入力として受け取ることを想定します。その上で、前述のように多数存在する NeRF の亜種を広く扱えるよう、オリジナルで導入された入出力変数である $(x,y,z,\theta,\phi)$ および $(r,g,b,\sigma)$ のみに依存する構造を設計しました。

大まかな概要としては、Fig.7 に示すように、まず与えられた NeRF を対象空間内で均一にサンプリングすることでグリッド表現を得ます。これを 3D Conv層でできたバックボーンに入力したのち、前述した FPN のように階層的に解像度を変更しながら特徴量を獲得し、それぞれで RPN を適用することで物体検出をおこないます。

| NeRF のグリッド化

シーン内のすべてのカメラと物体を含む直方体領域よりもやや大きな領域をカバーできる形で、対象空間を一様にグリッド化します。ここでの一様とは、各軸において等分割するというより、小さな立方体で埋め尽くすようなイメージが近いでしょう（追跡領域が立方体とは限らないため）。

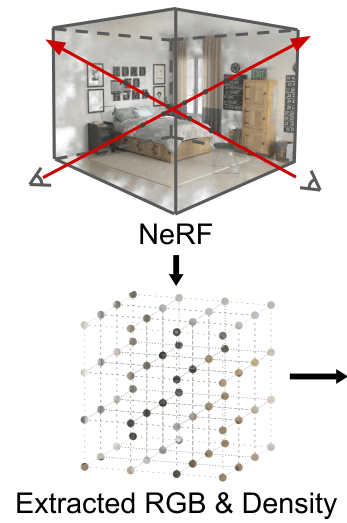
Fig.7 のこの部分。

次に、離散化した各座標における色の平均と密度を求めます。基本的には NeRF を学習するために用いた画像集合の視点群から得られる $(r,g,b)$ 値を平均しますが、カメラ角度が不明な場合、対象領域を囲む球面上から等方的にサンプリングして平均することとします。また、Fig.2 で示したように密度 $\sigma$ はカメラ角度に依存しないよう学習されるため、各グリッド座標ごとにその値が定まります。ただし、NeRF-RPN では密度を次の $\alpha$ に変換して用いることを提案しています：

\alpha={\rm clip}(1-e^{-\sigma\delta},0,1), ~~{\rm where}~~ \delta=0.01.

こうして得られる3次元グリッド表現の構成単位を、ボクセルと呼んだりもします。画像におけるピクセルに対応する言葉と考えればわかりやすいのではないかと思います。

このようにグリッド化を最初に噛ませることにより、NeRF という特殊な入力に対しても、一般的な物体検出のスキームを後段に接続できるようになるというわけですね。

| 特徴抽出器

与えられたグリッドを処理するバックボーンとして、NeRF-RPN では VGG19、ReNet-50、および Swin Transformer-S を採用し、比較しています。このとき、各モデルの2D Conv層が3D Conv層に置換されるなど、全体的に構成要素の3次元化がおこなわれました（3次元化するとメモリ消費が激しいため、ベースとなるモデルサイズは必ずしも大きくないといえます）。これに伴い、Swin Transformer では位置埋め込みも3次元化しています。

| 3D RPN

さて、ここまででピラミッド状に手に入った複数解像度の特徴量から、物体領域を推論するために、RPN を設計します。ここでの目的は、画像内物体検出における RPN と同様、物体が存在しそうな直方体領域の提案、および物体の存在確率の予測です。画像分野では一般に提案領域が縦横軸に沿った長方形であるのに対し、本手法で提案される RPN は Oriented R-CNN を応用し、鉛直方向を軸に回転したような直方体も取り扱います。

ただし、設置面は水平であるよう制約されるため、ピサの斜塔のように地面に対して傾いた物体を傾斜を考慮して綺麗に囲むことはできません（そのような対象は稀だと思いますが）。

NeRF-RPNでは、RPN としてアンカーベースとアンカーフリーなものの両方が考案されました。以下でそれを見ていきましょう。

★ アンカーベースの 3D RPN

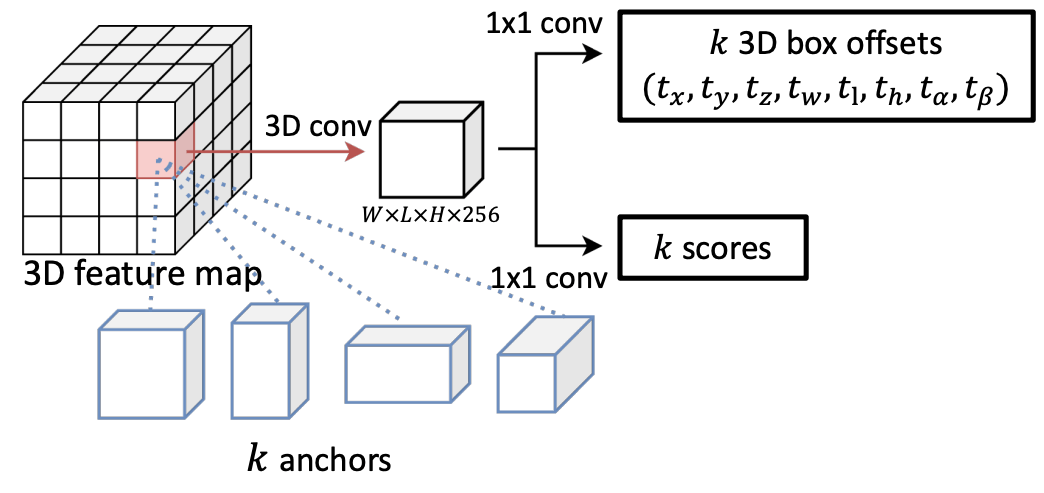
Fig.8. アンカーベース RPN。NeRF-RPN: A general framework for object detection in NeRFs より引用。

アンカーベースの 3D RPN は、基本的には Oriented R-CNN における RPN の単なる3次元拡張です。ここでは、異なるアスペクト比と大きさの直方体候補（アンカー）を、仮想的に特徴マップの各ボクセルに配置します。実際には数層から成る 3D CNNs で特徴マップをさらに処理して、それぞれのアンカーの特徴量として看做すという具合です。

これらに対して、実際に検出される直方体のオフセットと、この直方体内に物体が存在する確率を予測します。各オフセット値は、Oriented R-CNN のスキームを応用し、スケール非依存の正規化値を出力するよう訓練されます。具体的には $\bm{t}=(t_x,t_y,t_z,t_w,t_l,t_h,t_\alpha,t_\beta)$ を予測しますが、これらは着目している特徴ピラミッドにおけるアンカーパラメータと、実際に出力したい検出領域のパラメータを、次のような関係で結びつけます：

\begin{aligned} t_x&=\frac{x-x_a}{w_a}, & t_w&=\ln\left(\frac{w}{w_a}\right),\\ t_y&=\frac{y-y_a}{l_a}, & t_l&=\ln\left(\frac{l}{l_a}\right), \\ t_z&=\frac{z-z_a}{h_a}, & t_h&=\ln\left(\frac{h}{h_a}\right), \\ t_\alpha&=\frac{\Delta \alpha}{w}, & t_\beta&=\frac{\Delta \beta}{l}. \\ \end{aligned}

ただし、Fig.9 に図示するように、 $x,y,z$ は補正されたアンカー位置、 $w,l,h$ は補正されたアンカーサイズ、 $\Delta\alpha, \Delta\beta$ は最終的な提案領域（黒線）と補正されたアンカー表面（緑線）の接点が、補正アンカーの中心からどれだけずれているか（＝回転）を表す値です。同様に、添字に $a$ がつく $x_a$ 等の変数は、参照される元アンカーにおけるパラメータを表しています。

直感的には、位置のずれがアンカーサイズに対してどれくらいの比率か、およびアンカーに対する補正後のサイズ比率が対数スケールでどれくらいかを予測する、と考えれば良さそうです。

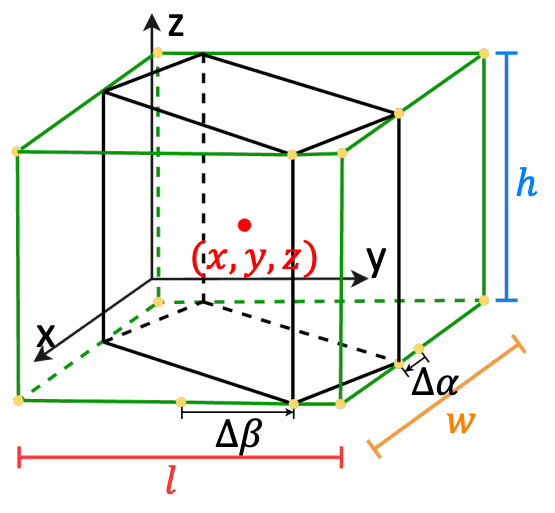
Fig.9. アンカーベース RPN。NeRF-RPN: A general framework for object detection in NeRFs より引用。

また、このようにパラメタライズされた領域は必ずしも直方体にはならないため、Oriented R-CNN に倣った変換を用いた後処理により、最終的に直方体領域が提案されるようにします。

提案領域中に物体が存在するか否かのラベルは、正解として与えられる直方体との空間的な重なり度（IoU）に基づきます。 IoU は0から1の値を取りますが、 IoU が0.35以上、または、ある正解領域に対して最も高い IoU を持つ提案領域に対しては正のラベルを付与します。また、正のラベルが振られなかった提案領域のうち、いずれの正解領域との IoU も0.2以下のものには負のラベルを与えます。正でも負でもないそのほかの提案領域は、後続の計算では無視されます。

ちなみに、 IoU は直感以上に厳しい指標で、目視ではそれなりに重なっているように見えても数値上は意外と低いということがよくあります（2次元で可視化してくれている以下の記事などが理解しやすいです）。3次元ではその傾向がより強まるため、上記は一見緩い基準に思える裏で、実際は直感的に一定以上妥当な閾値といえるのではないかと思われます（実際、同じ大きさの立方体を2つ用意して、各辺が8割ずつの長さで重なるようにすると、IoU が0.35程度になります）。

以上を踏まえ、次の損失関数の和に基づいて、アンカーベースの 3D RPN は訓練されます。

オフセット値の回帰（平滑化 $L_1$ 損失）
物体存在確率の分類（二値クロスエントロピー）

★ アンカーフリーな 3D RPN

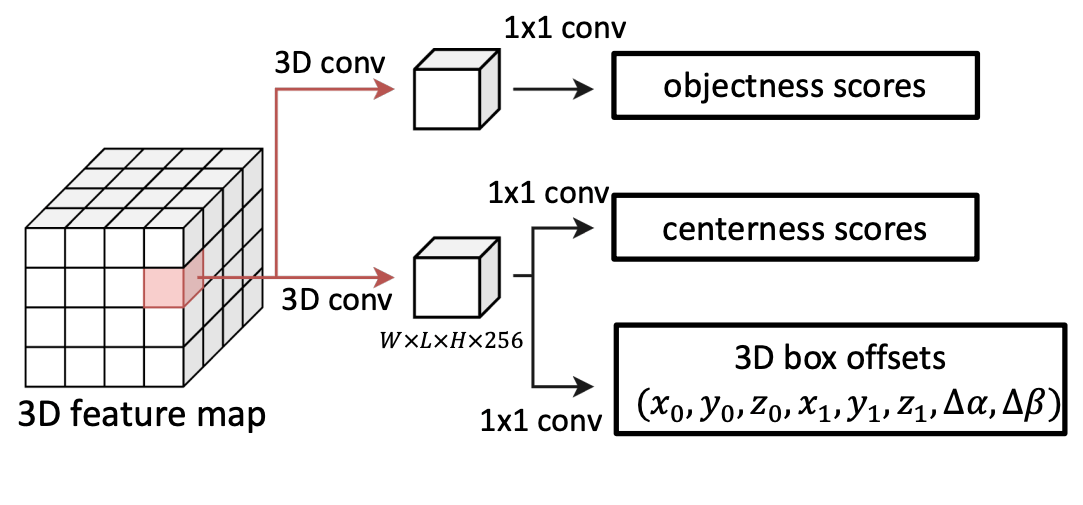
Fig.10. アンカーフリー RPN。NeRF-RPN: A general framework for object detection in NeRFs より引用。

アンカーフリー手法は、提案領域の位置やサイズ、物体存在確率を直接回帰する仕組みです。そのため、アンカーベース手法におけるアンカーごとの IoU 計算を削減できるという利点を持ちます。

NeRF-RPN では、FCOS と呼ばれる2次元での既存手法を拡張してアンカーフリーな 3D RPN を考案しました。具体的には、特徴マップの各ボクセルにおいて、物体存在確率 $p$ 、中心性スコア $c$ 、検出領域のオフセット $\bm{t}=(x_0,y_0,z_0,x_1,y_1,z_1,\Delta\alpha,\Delta\beta)$ を出力します。ここで予測されるオフセット値は、次の $\bm{t}_i^*=(x_0^*,y_0^*,z_0^*,x_1^*,y_1^*,z_1^*,\Delta\alpha^*,\Delta\beta^*)$ を対象に回帰推定されます：

\begin{aligned} x_0^*&=x - x_0^{(i)}, & x_1^*&=x_1^{(i)} - x,\\ y_0^*&=y - y_0^{(i)}, & y_1^*&=y_1^{(i)} - y, \\ z_0^*&=z - z_0^{(i)}, & z_1^*&=z_1^{(i)} - z, \\ \Delta\alpha^*&=v_x^{(i)} - x, & \Delta\beta^*&=v_y^{(i)} - y. \\ \end{aligned}

ただし、 $x,y,z$ はボクセル位置です。また、 $x_0^{(i)}<x_1^{(i)}$ は Fig.11 において、最終的な提案領域（黒線）を囲む空間軸に並行な直方体（緑線）における両側境界面の $x$ 座標を表しています。 $y_0^{(i)}$ なども各軸において同様です。また、 $v_x^{(i)}$ は提案領域の最も $y$ 座標が大きい頂点の $x$ 座標、 $v_y^{(i)}$ は最も $x$ 座標が大きい頂点の $y$ 座標を表します。直感的には、ボクセルの座標（赤点）から領域各面への距離等を予測していると考えれば理解しやすいかと思います。

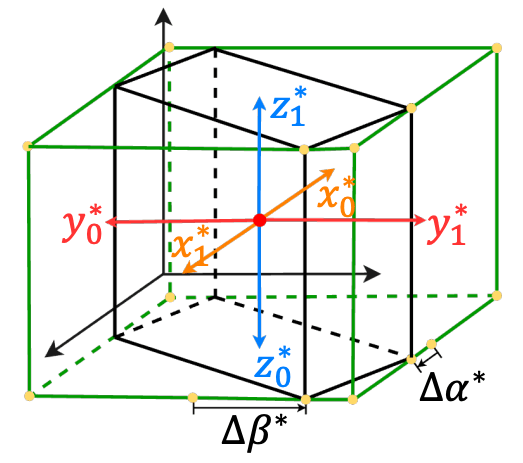
Fig.11. アンカーフリー RPN。NeRF-RPN: A general framework for object detection in NeRFs より引用。

添字の $i$ がなにを表しているのかという点ですが、NeRF-RPN の論文中では『 $i$ 番目の正解となる方向付き直方体』という説明がなされています。すると、モデル出力に対して回帰推定をおこなう対象値が正解の直方体の数だけ存在するという状況になるわけですが、ひとつの出力値が複数の正解に結びつくというのはなんだか変ですね。実際、後述する損失関数ではそのような計算は行われていない模様でした。

ここで、アンカーベース RPN が Oriented R-CNN の素直な3D拡張であることを踏まえ、このアンカーフリー RPN の元となる FCOS を参照すると、この $i$ は『特徴ピラミッドにおける $i$ 番目の層』を表していると考えるのが妥当そうであることがわかります。その上で、各ボクセルに対する正解領域は、単純にそのボクセルを内部に含むものを選択するという形となります。

論文中では、アンカーベース RPN の損失関数定義時に記号定義なしで添字 $i$ が登場しているのですが、内容的にこれがまさに『 $i$ 番目の正解領域』として用いられているようでした。この流れをうっかり引き摺ってしまったのかもしれませんね。

さらに、物体の中心性スコアは、次のスコア $c^*$ を正解として学習されます：

c^*=\sqrt{\frac{\min (x_0^*,x_1^*)}{\max (x_0^*,x_1^*)} \frac{\min (y_0^*,y_1^*)}{\max (y_0^*,y_1^*)} \frac{\min (z_0^*,z_1^*)}{\max (z_0^*,z_1^*)}}.

直感的には、3次元の各軸において、注目している座標から直方体の向かい合う両面への距離を考えていると解釈すればよさそうです（Fig.11 の橙、赤、水色の矢印）。各距離ペアが等しくなるほど $c^*$ は1に近づき（＝中心）、逆にどこかの面に接近するほど0になります（＝中心ではない）。

以上を踏まえ、次の損失関数の和に基づいて、アンカーフリーな 3D RPN は訓練されます。

オフセット値の回帰（ IoU 損失および $\Delta\alpha$ と $\Delta\beta$ に対する平滑化 $L_1$ 損失）
物体存在確率の分類（フォーカル損失）
中心性スコアの分類（二値クロスエントロピー）

| 追加の損失関数

NeRF-RPN では、精度向上と偽陽性率低減のために、追加の損失関数を提案しています。二段構えのモジュールによって領域推定をさらにリファインしようとする意図が読み取れます。

とはいえ、後段のアブレーションスタディにより、これらの追加損失は今回の実験スコープで効果がないことが判明しているため、読み飛ばしていただいても構いません。

★ 物体性分類

こちらは、アンカーベースやアンカーフリーのどちらを採用したかにかかわらず、RPN の後段に付け加えられる損失関数です。入力としてはバックボーンから得られた特徴ピラミッドと RPN により出力された関心領域を受け取り、その領域内物体が存在する確率、および関心領域のオフセットを調整するパラメータを改めて推定します。

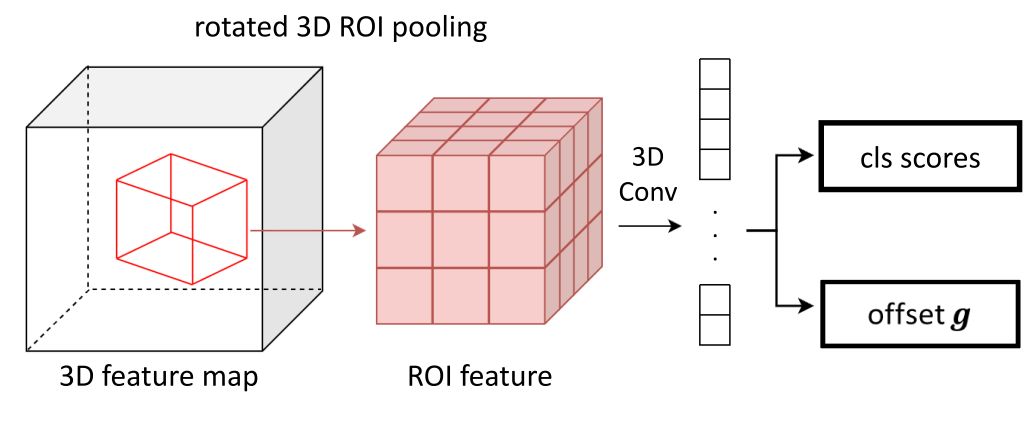
Fig.12. 物体性分類の概要。NeRF-RPN: A general framework for object detection in NeRFs より引用。

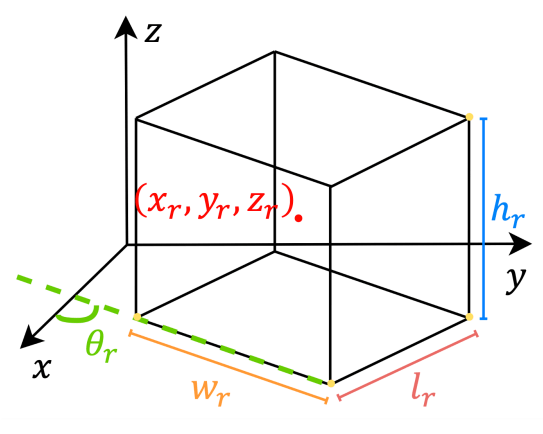
RPN から受け取る提案領域は、その中心座標 $(x_r,y_r,z_r)$ 、各辺の長さ $(w_r,l_r,h_r)$ 、および $z$ 軸周りの回転角 $\theta_r\in[-\frac{\pi}{2},\frac{\pi}{2}]$ で与えられるとします。これを各特徴ピラミッドのスケールに合わせて適切に拡縮したのち、トリリニア補間やゼロパディングを用いながら特徴マップの該当ボクセル群をくり抜きます。こうして抽出される領域は、元の提案領域の大きさにかかわらず一辺が3ボクセルの立方体になるよう固定長に調整され、後続の計算に用いられます（Faster R-CNN におけるいわゆる関心領域プーリングと同様です）。

Fig.13. 物体性分類の概要。NeRF-RPN: A general framework for object detection in NeRFs より引用。

さて、こうして得られた関心領域特徴から、物体か否かを二値分類する確率値を推定します。ここでの『物体である』というラベルは、関心領域がいずれかの正解領域と0.25以上の IoU を持つ場合に付与されます。それ以外は全て非物体として処理されます。

さらに、提案領域を最終調整するスケール非依存のオフセット $\bm{g}=(g_x,g_y,g_z,g_w,g_l,g_h,g_\theta)$ も推定します。補正後の領域パラメータ $(x,y,z,w,h,l,\theta)$ とは次のように結びついています：

\begin{aligned} g_x&=\frac{(x-x_r)\cos\theta_r+(y-y_r)\sin\theta_r}{w_r}, & g_w&=\ln\left(\frac{w}{w_r}\right),\\ g_y&=\frac{(y-y_r)\cos\theta_r-(x-x_r)\sin\theta_r}{l_r}, & g_l&=\ln\left(\frac{l}{l_r}\right), \\ g_z&=\frac{z-z_r}{h_r}, & g_h&=\ln\left(\frac{h}{h_r}\right), \\ g_\theta&=\frac{\theta-\theta_r}{2\pi}. \\ \end{aligned}

これは一見複雑そうに見えますが、 $\theta_r$ による $xy$ 平面回転を考慮した表式になっているだけで、本質的にはほとんどアンカーベース RPN と同じ推定対象であることがわかります。実際、例えば $\theta_r=0$ として空間軸と並行な直方体領域を考えれば、とてもそっくりな形になります：

\begin{aligned} g_x&=\frac{x-x_r}{w_r}, & g_w&=\ln\left(\frac{w}{w_r}\right),\\ g_y&=\frac{y-y_r}{l_r}, & g_l&=\ln\left(\frac{l}{l_r}\right), \\ g_z&=\frac{z-z_r}{h_r}, & g_h&=\ln\left(\frac{h}{h_r}\right), \\ g_\theta&=~~\frac{\theta}{2\pi} & & ~~{\rm when}~~ \theta_r=0. \\ \end{aligned}

損失関数もアンカーベース RPN と同等で、物体性スコアの二値クロスエントロピー、およびオフセットの $L_1$ 損失から構成されます。

★ 2次元射影損失

こちらは、3次元の提案領域を、あるカメラ角度から見た視点の2次元領域に落とし込んで回帰推定する損失関数です。発想としては既存の3次元物体検出手法に通ずるものを感じます。

ただ、NeRF-RPN では既に立体空間で提案領域を学習しているため、この2次元射影損失はモデルに新たな情報を授けてはくれないようです。実際、後述の実験章では、この追加損失による有意な性能向上は見られないことが確認されました。したがって、ここではアイデアの紹介に留めます。

データセット構築

さて、ここまで NeRF-RPN の仕組みについて見てきましたが、深層学習においてモデル構築と同程度、あるいはそれ以上に重要なものはデータです。著者らも述べている通り、少なくとも本論文が発表された当時は NeRF における代表的な物体検出データセットは存在しませんでした。そのため、今回の問題設定に適したベンチマークの作成も並行しておこなわれました。

そこで冒頭にも述べたように、室内の合成シーンデータセットである Hypersim と 3D-FRONT、および実世界の室内シーンデータセットである ScanNet と SceneNN の一部を組み合わせ、正解となる直方体領域を慎重にアノテーションしました。前提として、これらのデータセットは必ずしも NeRF の学習を想定して設計されていないため、著者らは NeRF の再構成品質等に基づいてデータクリーニングをおこなうなどして、データセットの品質を担保する工夫をしています。

各データセットから選ばれたシーン数やアノテーションされた領域数は下表で確認できます。

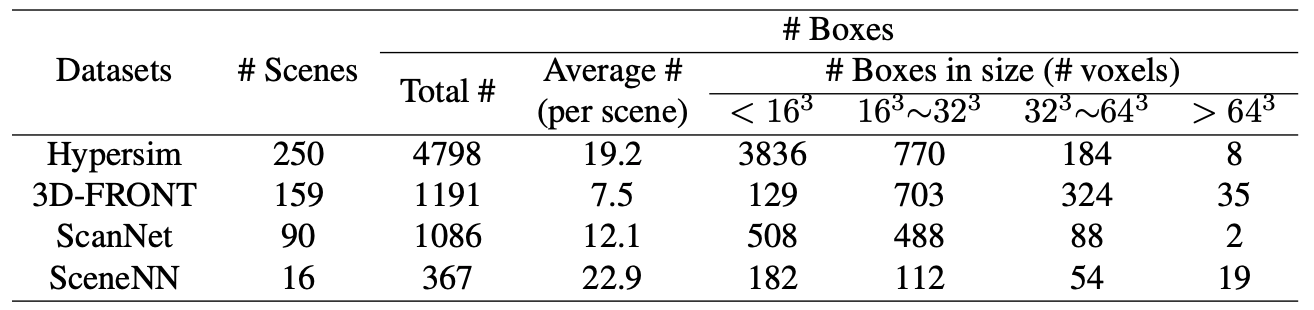
Tab.1. 構築された室内物体検出用データセットの概要。NeRF-RPN: A general framework for object detection in NeRFs より引用。

また、実際に構築されたデータセットは以下のようになっています。

Fig.14. 3D-FRONT から構築された物体検出用データセットのサンプル。1段目と2段目は NeRF 自体の再構成品質と正解領域の品質を示している。3段目と4段目は、多様な物体に対してアノテーションされていることを示す。NeRF-RPN: A general framework for object detection in NeRFs より引用。

学習と評価

| 学習

メモリ的な制限から、NeRFのグリッド化における1辺のボクセル数は Hypersim で200、その他のデータセットで160が最大値に定められました。また、入力シーンには $xy$ 軸でのランダム反転や、 $z$ 軸周りのランダムな直角回転がオーグメンテーションとして適用されました。加えて、 $z$ 軸周りにさらに0.5の確率で範囲 $[-\frac{\pi}{18},\frac{\pi}{18}]$ の回転をさせるとRPN の検出精度が大きく向上したようです。

アンカーベース手法ではさらにアンカーのためのハイパーパラメータとして、13種類の基準アスペクト比が定められました。それぞれは、特徴ピラミッドの各階層において、最も短い辺の長さを一致させて用います。またFaster R-CNNでの工夫と同様に、訓練時は想定しうる全てのアンカーを同時に計算するのではなく、各シーンに対して都度256個のアンカーをランダムに選んで損失を計算することで効率化が図られました。

| 評価

評価時は、RPN により得られた関心領域のうち、まず中心がシーン境界から逸脱しているものを除外します。その上で、各階層における上位2500件の提案領域を独立に選んだのち、NMS（Non-Maximum Suppression：非極大値抑制）により冗長な提案が排除され、最終出力となります。

また、NeRF-RPN の論文中には特に記されていませんが、アンカーフリー RPN について、FCOS では中心性スコアを物体存在確率に乗算することで、中心から離れたボクセルの予測を抑制する旨が記述されており、NeRF-RPN もこれに倣っているものと思われます。これは、正解領域の中心から離れた座標での予測が比較的低品質になりやすいとの観察に基づく工夫のようです。

実験と結果

| アブレーションスタディ

ある要素を除いて実験することで、各要素がどのように最終性能に寄与しているかを比較評価する実験をアブレーションスタディ（無理に訳すと切除実験）といいますが、NeRF-RPN でもバックボーンや RPN の様式、NeRF 表現のグリッド化におけるサンプリング方法、および損失関数についてこれをおこなっています。

★ バックボーンや RPN の様式

3種類のバックボーンと2種類の RPN の組み合わせについて比較しています。同じバックボーン同士を比較すると、アンカーフリー RPN が全体的により高い AP（平均適合率）を示していることがわかります。また、Recall（再現率）は 3D-FRONT と ScanNet にて概ね同等ですが、Hypersim においてはアンカーフリー RPN が優位に高い性能を示しています。

著者らはこの結果について、『アンカーフリー RPN における中心性スコア予測が物体中心から離れた予測を抑制することで、領域中心が物体の重心からずれていたり、NeRF 表現がノイジーな場合に役立ちうる』こと、および『アンカーベース RPN は限られたアスペクト比の候補によって性能が制約されている』ことを理由として考察しています。

また、バックボーン間の比較をすると、一般に VGG19 が Recall と AP ともによりよい結果であるとしています。一方で、アンカーベース RPN 内の比較では Hypersim における Swin-S の結果が突出していることに触れ、Hypersim のような比較的ノイジーで複雑な NeRF シーンにおいては、より広い受容野や豊かな意味表現が重要である可能性を述べています。

Tab.2. バックボーンと RPN の比較。 ${\rm AP}_{25}$ などの添字は、その数値が IoU の閾値であることを表す。NeRF-RPN: A general framework for object detection in NeRFs より引用。

★ NeRF のサンプリング戦略

先述のように、NeRF における密度は視点非依存ですが、色情報は視点依存です。したがって、グリッド化に際してどのように視点をサンプリングするかによって、NeRF 入力が変わります。

著者らは複数のサンプリング方法を比較し、興味深いことに『密度情報のみを用いる』ものが、物体を検出するという用途においては全体的に最も高性能であると結論づけました。他方で、より下流の物体の種類の分類や、二次的な物体構造の検出には色情報が有用である可能性についても言及されています。

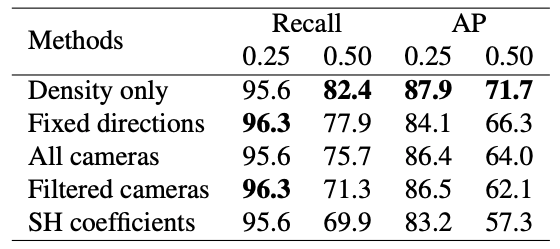
Tab.3. NeRF のサンプリング方法比較。3D-FRONT において、VGG19 とアンカーフリー RPN で実験。NeRF-RPN: A general framework for object detection in NeRFs より引用。

★ 損失関数

提案領域のオフセット予測に関する損失関数について比較実験し、Tab.4 のような結果を得ています。Tab.4 の説明にも記したように特定データセットとバックボーンにおける実験ですが、いずれにおいても IoU 損失が全体的によい性能を記録しています。

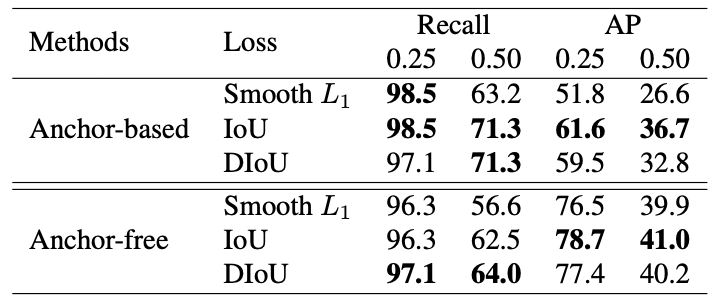
Tab.4. 提案領域に関する損失関数比較。3D-FRONT において、Swin-S で実験。NeRF-RPN: A general framework for object detection in NeRFs より引用。

また、提案された追加損失についても評価しています。まず物体性分類ですが、期待に反し、AP が大幅に低下してしまっています。原因のひとつとして、特徴ピラミッドの（特に圧縮された側の）解像度の低さが悪影響を及ぼしているとの仮説が立ててられています。

Tab.5. 物体性分類損失の比較。3D-FRONT において、Swin-S で実験。NeRF-RPN: A general framework for object detection in NeRFs より引用。

また、Tab.6 は2次元射影損失の導入有無による比較実験の結果です。こちらは性能が大幅に低下するということはありませんでしたが、有意に向上するといったこともなく、3D RPN の学習によりすでに十分な情報量を獲得できることを裏打ちしています。

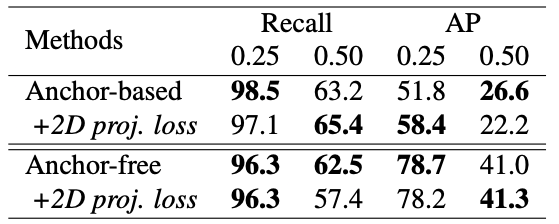
Tab.6. 2次元射影損失の比較。NeRF-RPN: A general framework for object detection in NeRFs より引用。

| 定性結果

ここまでの結果を踏まえ、VGG19 とアンカーフリー RPN の組み合わせで物体検出した結果の例が Fig.15 です。左から順に、入力された NeRF、提案の確信度を表すヒートマップ、および提案された直方体領域を示しています。全体的に良好な結果に見えますが、著者らは、入力となる NeRF の品質が悪いほど物体検出結果にも悪影響が出ることにも触れています。

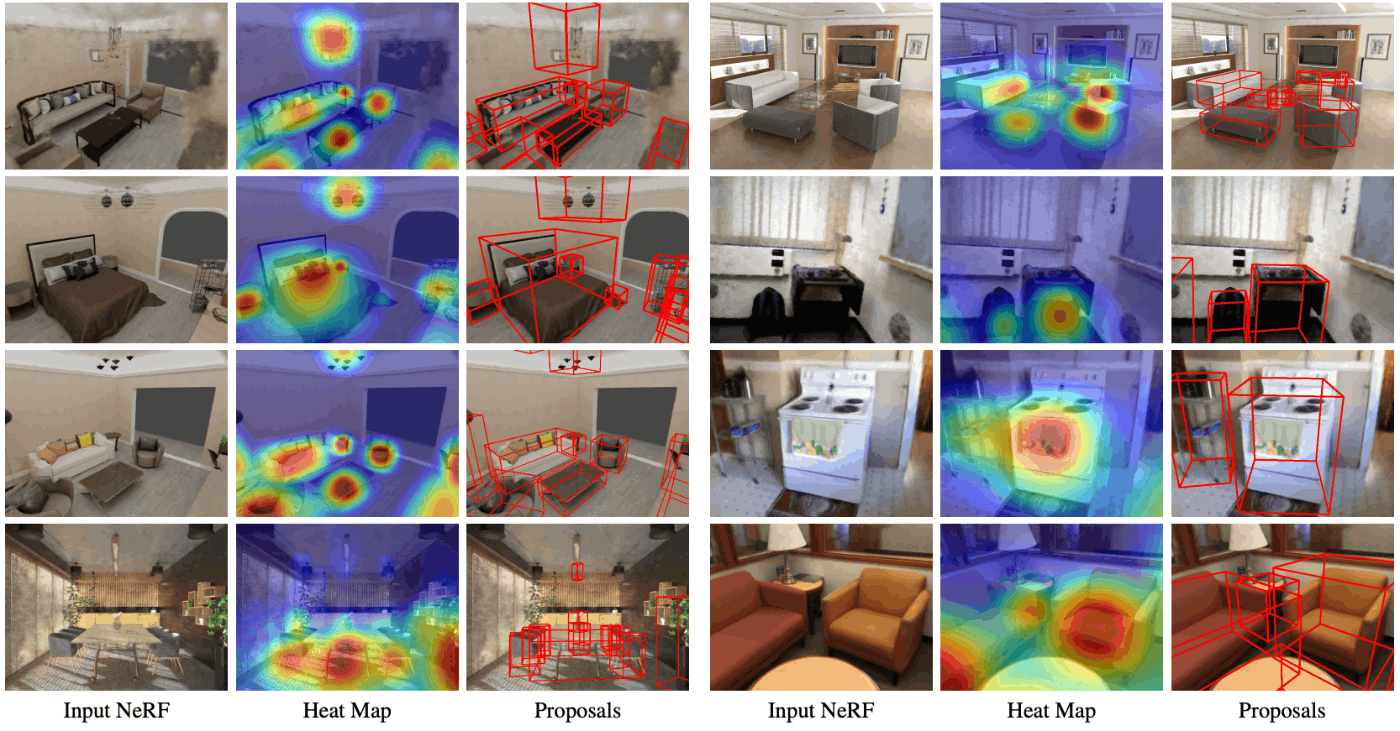
Fig.15. NeRF-RPN: A general framework for object detection in NeRFs より引用。

Fig.16 には検出失敗例が示されています。特に、本研究で構築されたベンチマークは主物体に焦点を当てたデータセットのため、より小さく副次的な物体の検出は今後の展望であるとしています。

Fig.16. (a) (b) は提案すべき領域が欠けていたり、別々であるべき領域が融合してしまったケース。(c) は回転状態の推定失敗、(d) は小さな物体や二次的な物体の検出に失敗したケース。NeRF-RPN: A general framework for object detection in NeRFs より引用。

応用例や発展性、あるいはまとめと呼ばれる類のもの

NeRF-RPN の論文では、この手法の応用例としてシーン編集が挙げられています。画像編集における対象消去に通ずるものがありますが、検出領域の NeRF 密度を 0 とすることで、あたかもその物体が存在しないかのように編集するというものです。とはいえ、Fig.17 を見てもわかるように、消去した物体と床の設置面が不自然にぼやけている（元々その箇所を NeRF 内で表す視点はなかった）ため、この方針で応用するにしても更なる研究は必要そうです。

Fig.17. シーン編集の例。NeRF-RPN: A general framework for object detection in NeRFs より引用。

などと執筆していたら、2023年にはより多彩かつ精緻に NeRF を編集可能な NeRFshop のような手法も登場してきており、界隈がますます盛り上がってきていることが感じ取れます。このように、シーン編集の方向性での応用はそれ専門の手法が発展しつつあるため、今後 NeRF-RPN が差し込まれる余地があるかは疑問符ではあります。が、物体検出そのものが画像分野でも発展してきたように、立体空間の新たな表現形式である NeRF の上で同様の機能を搭載することには、今後ますます意義が生じていくことが期待されます。

NeRF の紹介章でも触れたように、昨今では NeRF 自体の高速化や必要視点の小規模化、またコモディティ化が進んでおり、今後も進んでいくでしょう。現状の学習速度や処理速度ではまだまだ現実的ではありませんが、例えば将来的には、車載カメラを用いた自動運転支援やドローン技術への応用など、期待（というより妄想）が膨らみます。

一方で、今回の手法は限定的なシーンで実験評価されているため、より一般的な環境へ汎化するかも重要な観点です。室内のように物体がある程度整然と並んでおり、物体形状も直方体に沿うものが多いシーンと異なり、屋外では対象となる物体の形状や配置に関する複雑さが増大するはずです。これらがデータセットの単なる拡充で解決するのか、更なる手法の改善が必要なのかも含め、今後も検討していけるとよさそうですね。

参考文献

NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis [Mildenhall et al., ECCV, 2020]
NeRF-RPN: A general framework for object detection in NeRFs [Hu et al., 2022]
NeRF in the Wild: Neural Radiance Fields for Unconstrained Photo Collections [Brualla et al., CVPR, 2021]
Neural Scene Flow Fields for Space-Time View Synthesis of Dynamic Scenes [Li et al., CVPR, 2021]
pixelNeRF: Neural Radiance Fields from One or Few Images [Yu et al., CVPR, 2021]
Instant Neural Graphics Primitives with a Multiresolution Hash Encoding [Müller et al., SIGGRAPH, 2022]
MERF: Memory-Efficient Radiance Fields for Real-time View Synthesis in Unbounded Scenes [Reiser et al., 2023]
F2-NeRF: Fast Neural Radiance Field Training with Free Camera Trajectories [Wang et al., CVPR, 2023]
PAC-NeRF: Physics Augmented Continuum Neural Radiance Fields for Geometry-Agnostic System Identification [Li et al., ICLR, 2023]
Latent-NeRF for Shape-Guided Generation of 3D Shapes and Textures [Metzer et al., 2022]
Magic3D: High-Resolution Text-to-3D Content Creation [Lin et al., 2022]
Instruct 3D-to-3D: Text Instruction Guided 3D-to-3D conversion [Kamata et al., 2023]
Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks [Ren et al., NeurIPS, 2015]
Feature Pyramid Networks for Object Detection [Lin et al., CVPR, 2017]
Oriented R-CNN for Object Detection [Xie et al., ICCV, 2021]
FCOS: Fully Convolutional One-Stage Object Detection [Tian et al. ICCV, 2019]
NeRFshop: Interactive Editing of Neural Radiance Fields [Jambon et al., PACMCGIT, 2023]

参考資料

https://tech.isid.co.jp/entry/nerf_tips

https://note.com/npaka/n/n496e79df56dc

お知らせ

少しでも弊社にご興味を持っていただけた方は、お気軽にご連絡頂けますと幸いです。まずはカジュアルにお話を、という形でも、副業を検討したいという形でも歓迎しています。

https://recruit.zenkigen.co.jp/career

脚注

記事執筆当時。 ↩︎

ZENKIGENテックブログPublication

私たちは「はたらく人の理想」をつくるために、ITと科学で組織課題に立ち向かうAIテックカンパニーです。「テクノロジーを通じて人と企業が全機現できる社会の創出に貢献する」のVisionのもと、人の感覚に寄り添うテクノロジーを用いたでサービスを展開しています。