juliaのLuxでBayesian Neural ODEしてみる

summary

juliaで実装のBayesian Neural Ordinary Differential EquationsをLuxで再現するブログです．
全体コードは，機械学習訓練と，モンテカルロ法でサンプリングの二つの部分に分かれています
その中で，機械学習訓練の部分のみ，Luxに変更しています．
（サンプリングの方は，あまり変更なく，実行可能だったと思います．）

環境設定

julia 1.11.1
その他パッケージは適宜入れています．
Fulxはなくても可能と認識していますが，NeuralODEのためのDiffEqFluxは必要です．

目的

juliaを勉強するのに当たって，Bayesian Neural Ordinary Differential EquationsをLuxで再現しようとした際の記録か，記憶です．

Bayesian Neural Ordinary Differential Equationsは，約5？年前の論文で，元コードは，Fluxというライブラリで実装されています．最近では，Luxが開発され，主流っぽいです．
（Fluxもまだ使われていると思いますが，Luxに移行中らしいです．知らんけど，）

詳細は忘れましたが，julia 1.11.1で元コードを回そうと思ったら，全然うまくいかなくて，Luxに変更して，うまく行くようにしたという次第です．

元論文

Bayesian Neural Ordinary Differential Equationsでは，機械学習訓練後に，そのパラメータを固定するのではなく，確率変数と見て，ハミルトニアンモンテカルロ法でサンプリングしていたとお思います．それによって，不確実性を平均と分散から判断するみたいな感じだったと思います．

arxiv版しか見てませんが，式（3）の係数アルファの符号がなんで付いているか分かりません．
元コードの方は，ついていないです．

全体として，機械学習訓練と，モンテカルロ法でサンプリングの二つの部分に分かれています．
今回は，機械学習訓練の部分にのみフォーカスしています．
モンテカルロ法でのサンプリングは，時間がかかるので，サンプルサイズを減らした方が良いです

Flux と Lux

Flux と Lux については，しっかり理解できていないため説明できません，
他のブログを参考にしてください．

結果

得られる結果の図を先に見せます．

ロス関数

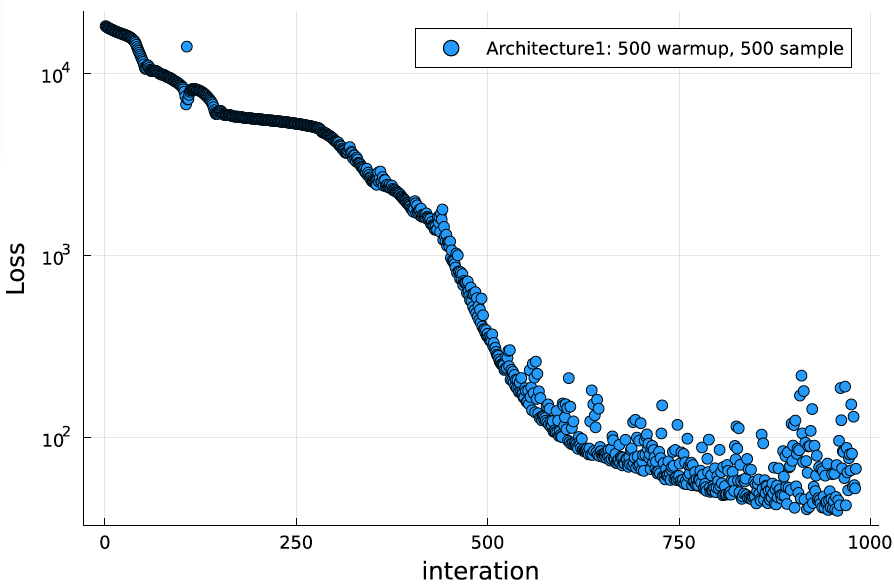
ロスの訓練後サンプリング

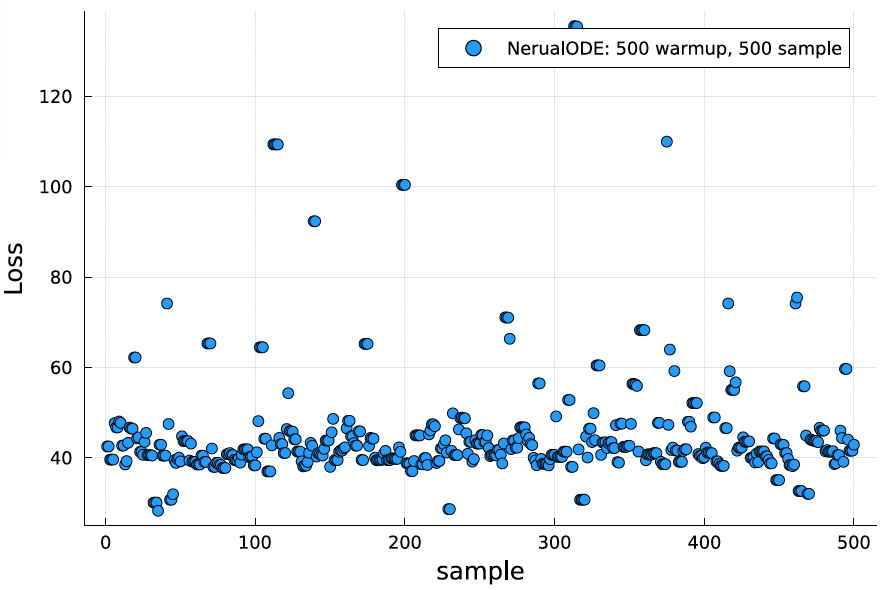
phase space plot

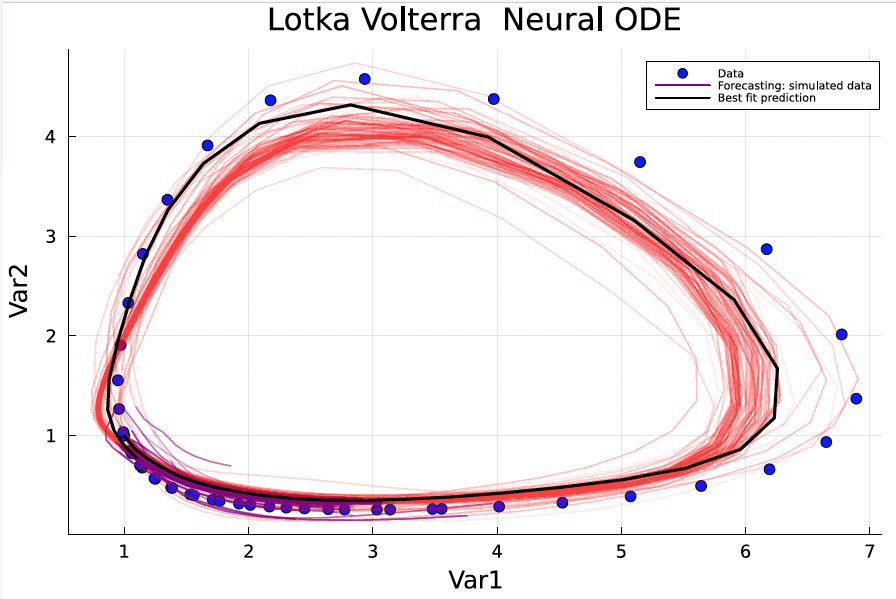
予測

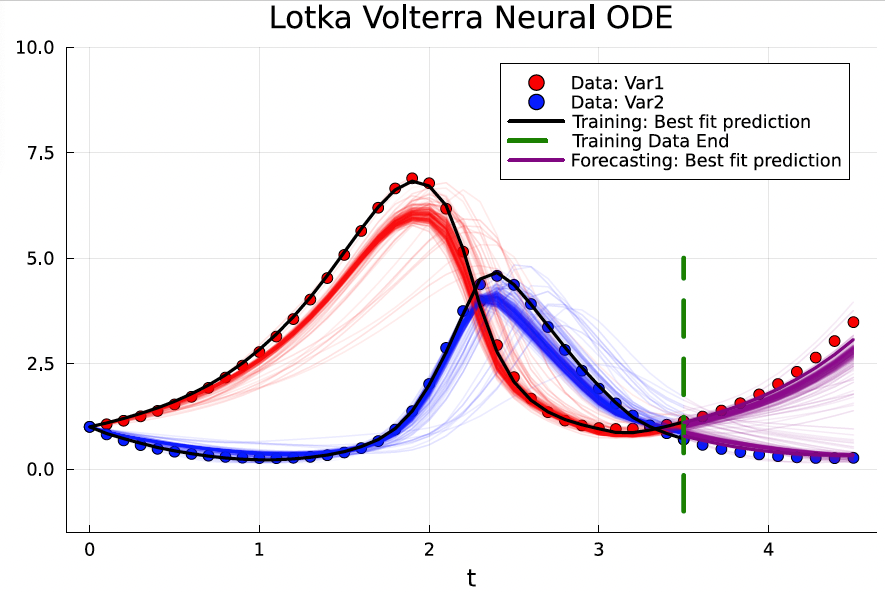
コード

コード

sample.jl

# SciML Libraries
using SciMLSensitivity, DifferentialEquations
using Lux, Zygote
using Random, Plots, AdvancedHMC, MCMCChains, StatsPlots, ComponentArrays, JLD2
using Optim, OrdinaryDiffEq, ComponentArrays, DiffEqFlux, Optimization, OptimizationOptimisers


function lotka_volterra!(du, u, p, t)
  x, y = u
  α, β, δ, γ = p
  du[1] = dx = α*x - β*x*y
  du[2] = dy = -δ*y + γ*x*y
end

# Initial condition
u0 = [1.0, 1.0]
# Simulation interval and intermediary points
tspan = (0.0, 3.5)
tsteps = 0.0:0.1:3.5
datasize = length(tsteps)
# LV equation parameter. p = [α, β, δ, γ]
parameter = [1.5, 1.0, 3.0, 1.0]
# Setup the ODE problem, then solve
prob_ode = ODEProblem(lotka_volterra!, u0, tspan, parameter)
mean_ode_data = ComponentArray{Float64}(solve(prob_ode, Tsit5(), saveat = tsteps))
ode_data = mean_ode_data .+ 0.1 .* randn(size(mean_ode_data)..., 30)

dudt2 = Lux.Chain(Lux.Dense(2, 20, relu),
                  Lux.Dense(20, 20, relu),
                  Lux.Dense(20, 20, relu),
                  Lux.Dense(20, 2))
rng = Random.default_rng()
p, st = Lux.setup(rng, dudt2)
prob_neuralode = NeuralODE(dudt2, tspan, Tsit5(), saveat = tsteps)

function predict_neuralode(p)
    Array(prob_neuralode(u0, p, st)[1])
end
pinit = ComponentArray{Float64}(p)

function loss_neuralode(p)
    pred = predict_neuralode(p)
    loss = sum(abs2, ode_data .- pred)
    return loss
end

loss_list = []
# Callback function to observe training
callback = function (p, l; doplot = false)
  push!(loss_list, l)
  if length(loss_list) % 10 == 0
    println("Current loss after $(length(loss_list)) iterations: $(loss_list[end])")
  end
  # plot current prediction against data
  if doplot
    pred = predict_neuralode(p)  # 予測値をここで計算
    plt = scatter(tsteps, ode_data[1,:,1], label = "data")
    scatter!(plt, tsteps, pred[1,:], label = "prediction")
    display(plot(plt))
  end
  return false
end
callback(pinit, loss_neuralode(pinit)...; doplot=true)

# Train using the Adam optimizer
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x, p) -> loss_neuralode(x), adtype)
optprob = Optimization.OptimizationProblem(optf, pinit)
result_neuralode = Optimization.solve(
    optprob, OptimizationOptimisers.Adam(0.005); callback = callback, maxiters = 1500)

l(θ) = -sum(abs2, ode_data .- predict_neuralode(θ)) - sum(θ .* θ)
function dldθ(θ)
    x, lambda = Zygote.pullback(l, θ)
    grad = first(lambda(1))
    return x, grad
end
metric = DiagEuclideanMetric(length(result_neuralode.minimizer)) 
h = Hamiltonian(metric, l, dldθ)
integrator = Leapfrog(find_good_stepsize(h, Float64.(result_neuralode.minimizer)))
kernel = HMCKernel(Trajectory{MultinomialTS}(integrator, GeneralisedNoUTurn()))
adaptor = StanHMCAdaptor(MassMatrixAdaptor(metric), StepSizeAdaptor(0.45, integrator))

# samples, stats = sample(h, kernel, Float64.(result_neuralode.minimizer), 500, adaptor, 500; progress = true)
# Number of chains to sample
# nchains=10
n_samples=500
n_adapts=500

samples, stats = sample(h, kernel, Float64.(result_neuralode.minimizer), n_samples, adaptor, n_adapts; progress =true)
losses = map(x-> x[1],[loss_neuralode(samples[i]) for i in 1:length(samples)] )
# losses = map(x -> loss_neuralode(x)[1], eachcol(samples))

############################ PLOT LOSS sample ##################################
scatter(losses, xlabel = "sample", ylabel = "Loss",  label = "Architecture1: 500 warmup, 500 sample")
###########################PLOT RETRODICTED DATA#########################
pl = scatter(tsteps, mean_ode_data[1,:], color = :red, label = "Data: Var1", title = "Lotka Volterra Neural ODE")
scatter!(tsteps, mean_ode_data[2,:], color = :blue, label = "Data: Var2", xlabel = "t", ylims = (0, 10))

for _ in 1:300
    resol = predict_neuralode(samples[100:end][rand(1:400)])
    plot!(tsteps, resol[1,:], alpha=0.04, color = :red, label = "")
    plot!(tsteps, resol[2,:], alpha=0.04, color = :blue, label = "")
    # plot!(resol[1,:],resol[2,:], alpha=0.04, color = :red, label = "")
end
# resol = predict_neuralode(samples[100:end][rand(1:400)])
# plot!(tsteps, resol[1,:], alpha=0.04, color = :red, label = "")
# plot!(tsteps, resol[2,:], alpha=0.04, color = :blue, label = "")

idx = findmin(losses)[2]
prediction = predict_neuralode(samples[idx][1:end-1])

plot!(tsteps, prediction[1,:], color = :black, w = 2, label = "")
plot!(tsteps, prediction[2,:], color = :black, w = 2, label = "Best fit prediction")

n = length(samples)
println("Length of samples:", n)

################################CONTOUR PLOTS##########################
pl = scatter(
    mean_ode_data[1,:],
    mean_ode_data[2,:],
    color = :blue, label = "Data",  xlabel = "Var1",
    ylabel = "Var2", title = "Lotka Volterra Neural ODE",
    legend = (0.85, 0.95), legendfontsize = 5,
)
for k in 1:size(ode_data, 3)
    scatter!(
        ode_data[1,:,k],
        ode_data[2,:,k],
        color = :blue, label = "",
    )
end

for k1 in 301:500
    σ = samples[k1][end]
    resol = predict_neuralode(samples[k1][1:end-1])
    for k2 in 1:10
        _resol = resol .+ σ .* randn.()
        label = ""
        plot!(_resol[1,:], _resol[2,:], alpha=0.04, color = :red, label = label)
    end
end

plot!(prediction[1,:], prediction[2,:], color = :red, w = 2, label = "Simulated data")
plot!(prediction[1,:], prediction[2,:], color = :black, w = 2, label = "Best fit prediction")


############################FORECASTING###################
function lotka_volterra!(du, u, p, t)
  x, y = u
  α, β, δ, γ = p
  du[1] = dx = α*x - β*x*y
  du[2] = dy = -δ*y + γ*x*y
end

# Initial condition
u0_f = [1.0, 1.0]

# Simulation interval and intermediary points
tspan_f = (0.0, 4.5)
datasize_f = length(0.0:0.1:4.5)
tsteps_f = [tsteps; range(tspan[2], tspan_f[2], length = datasize_f - datasize)]

# LV equation parameter. p = [α, β, δ, γ]
p = [1.5, 1.0, 3.0, 1.0]

# Setup the ODE problem, then solve
prob_ode_f = ODEProblem(lotka_volterra!, u0_f, tspan_f, p)
sol_ode_f = solve(prob_ode_f, Tsit5(), saveat = tsteps_f)
ode_data_f = hcat([sol_ode_f[:,i] for i in 1:size(sol_ode_f,2)]...)

prob_ode_f = ODEProblem(lotka_volterra!, u0_f, tspan_f, p)
mean_ode_data_f = Array(solve(prob_ode_f, Tsit5(), saveat = tsteps_f))
ode_data_f = cat(ode_data, mean_ode_data_f[:, datasize+1:end] .+ 0.1 .* randn(size(mean_ode_data_f, 1), size(mean_ode_data_f, 2) - datasize, 30), dims = 2)

prob_neuralode_f = NeuralODE(dudt2, tspan_f, Tsit5(), saveat = tsteps_f)

function predict_neuralode_f(p)
    Array(prob_neuralode_f(u0_f, p))
end

idx = findmin(losses)[2]
prediction_f = predict_neuralode_f(samples[idx])

training_end = 3.5

pl = scatter(
    mean_ode_data_f[1,:],
    mean_ode_data_f[2,:],
    color = :blue, label = "Data",  xlabel = "Var1",
    ylabel = "Var2", title = "Lotka Volterra  Neural ODE",
    legend = (0.8, 0.95), legendfontsize = 5,
)

for k in 1:size(ode_data_f, 3)
    scatter!(
        ode_data_f[1,:,k],
        ode_data_f[2,:,k],
        color = :blue, label = "",
    )
end

for k1 in 301:500
    σ = samples[k1][end]
    resol = predict_neuralode_f(samples[k1][1:end-1])
    for k2 in 1:10
        _resol = resol .+ σ .* randn.()
        label = ""
        plot!(_resol[1,:][1:datasize], _resol[2,:][1:datasize], alpha=0.02, color = :red, label = label)
        plot!(_resol[1,:][datasize+1:end], _resol[2,:][datasize+1:end], alpha=0.04, color = :green, label = label)
    end
end

plot!(prediction_f[1,1:datasize], prediction_f[2,1:datasize], color = :red, w = 2, label = "Training: simulated data")
plot!(prediction_f[1,datasize+1:end], prediction_f[2,datasize+1:end], color = :green, w = 2, label = "Forecasting: simulated data")
plot!(prediction_f[1,1:datasize], prediction_f[2,1:datasize], color = :black, w = 2, label = "Best fit prediction")

savefig("./results/ExtendedLV_Contour_Retrodicted_500_500_Arch2.pdf")

その他

サンプリングが遅いので，chain等を使ったら，早くなるのかと思ったんですが，早くならないですね．そして，1chainが終わるまで，サンプリングした値を持つので，メモリがきついです．

後，当然ですが，マルチスレッドでやった方がサンプリング早く終わります．
gpuでもやってみたんですが，訓練だけでも乗り切らないですね
（ご存知の方いれば，教えてください）

うるおぼえで記事書きましたので，動かない等のコメントあれば教えてください．
（何か修正点を忘れているような気がするのですが，思い出せません．）
コメントいただけたら，嬉しいです．

追記

やはり，そのままのコードでは動かないと思います．
コード修正しました．

原因として，function loss_neuralode(p)がpredを返すことで，lossだけにしろと，自動微分ライブラリZygoteがエラー吐きます．(最新の Optimization.jlはもうlossとpredを返す関数はサポートしないそうです．)

どこかで，ロスだけを渡すようにすれば良いのですが，忘れました．
とりあえず，function loss_neuralode(p)でlossだけ返すようにすれば動きました．
後．callbackのfunctionにpredを含まないようにしました．
また，callbackが綺麗に出るように更新しておきました．（03/05）