文章(データ)をベクトルにするとはどいうことなのか
TL;DR
モチベーション
どんな分野にも言えることですが、長いことにそこに浸かっていると初心を忘れてしまうものですよね。
自分も学生時代から数えて4,5年は機械学習関連の勉強をしたり開発をしているせいか、様々なデータ、例えば画像、音声、文章などをベクトルとして表現して、それらの間の類似度を計算するという行為に対して大した疑問も持つことがなくなってしまいました。
しかし、よくよく思い返してみると、文章のようなデータをベクトルとして表現することは全く直感的ではありませんし、そもそも日常会話くらいでしかベクトルという単語を使わない方にとって、その理解のハードルは非常に高いように感じます。
この記事では、対象読者に数学的素養は(ほんのちょっとしか)求めずに機械学習エンジニアがどんなニュアンスでこれらのデータをコンピュータ上で取り扱い、ビジネスや研究で活用しているのかを伝えることを目的としています。
よって、数学的・情報科学的な厳密性よりイメージしやくとっつきやすいものを目指しているので、その道の専門家の方々は是非自分たちにもそんな時代があったなあと多めに見て頂けると幸いです。
初めに、ベクトルとは
日常会話におけるベクトル
日常会話における"ベクトル"は『話のベクトルがズレている』といったような使い方をしますよね。ここで言うベクトルとは"向き・方向"を表していると思います。
数学・物理におけるベクトル
実際、"向き"という表現は本質を捉えており、数学的にベクトルとは"大きさ"と"向き"を持つ量を指します。
また物理学において"ベクトル"と相対する量として"スカラー"と呼ばれるものがあります。名前は仰々しいですが、スカラーとは簡単に言えば"1, 2, 3...,100"のような単体の値で、こちらは"向き"という情報を持ちません。
一方でベクトルはカッコ記号を用いて、(3,4)のように数字のペアで表される量です。このペアの個数は別に2個である必要性はなくて、3個でも100個でも、なんなら無限個でも良いのですが、それは少し難しい話になるので、取り敢えず有限個の数字のペアがベクトルであると言って良いでしょう。ここでペアとなる数字の個数を"次元"と呼びます。
このような数字のペアからなるベクトルは以下の図のように、平面や空間上にプロットすることでそのイメージが湧きやすくなるでしょう。原点からベクトルとして指定した座標を結ぶ線は向きを持ち、同時に大きさを持つことがイメージできるでしょう。

機械学習における(高次元空間の)ベクトルとその意味
機械学習の文脈では2や3と比べると非常に大きな次元数、例えば768次元のベクトルを良く扱います。
最近話題のChatGPTに代表される大規模言語モデル(LLM)の1つであるLlama 3.1 8B (Meta)というモデルは4,096次元にものぼるそうです。
先に結論からお話すると、我々人間は3次元空間以上の世界を考えることは出来ず、一般に不毛であるため、上述したような高次元(4次元以上)のベクトルとは数字の列であると考えるべきです。
日常会話や数学・物理におけるベクトルのイメージに引っ張られすぎると機械学習分野でよく交わされる高次元空間におけるベクトルが逆にイメージしづらくなってしまいます。
例えば、機械学習の文脈で良く話される言語モデルの1つであるBERTは入力された文章に対して768次元のベクトルを出力します。ここで「768次元空間ってなんだよ!」となる気持ちは分かるのですが、単に768個の数字が並んだ配列が入力された文章を表すベクトルと考えると良いでしょう。
実際に文章を与えると以下の写真のような数字の列が返されます。元の文章とは似ても似つかないですね笑

キーワード
コンピュータ上で類似度を調べるには
データをベクトルで表現しよう
人間の脳は非常に高性能であるため、2つの画像が似ているとか、音楽の雰囲気が似ているとか、文章が似ているということを半ば感覚的に判定することが出来ます。しかし、人間の判定にはどうしても主観が入ってしまったり、コンピュータの計算速度に比べて遅いという欠点が存在します。
そこで、このような類似度計算処理をコンピュータ上で高速に行いたいというモチベーションがあります。
ここで重要となる点が、コンピュータは"数字と四則演算(特に足し算)"しか扱えないということです。よって、上述の画像・音楽・文章といったデータを数字の列(すなわちベクトルですね!)で表現して上げる必要があるわけです。
内積というツールが便利すぎる件w
ここで新たな登場人物を紹介します。それがベクトルを用いて計算できる"内積"であり、これはその印象とは裏腹に実際には非常に強力なツールとなっています。
この内積は本来はベクトル同士のなす角度を計算するためのツールなのですが、どういうわけかこれを使うとベクトル同士の"類似度"が足し算と掛け算だけで計算できてしまうんです!(関連書籍などを読んだことのある人であればコサイン類似度という表現を聞いたことがあるかもしれません)
数学Bの教科書の内積の項を読んでみると、『内積というものがあり、以下のような計算方法によりベクトル同士の角度(
以下にさらっと、計算方法を示しますが、まあ読み飛ばしてもらっても大丈夫です笑
(2次元平面における)内積(
)の計算方法 \cdot
\vec{a} \cdot \vec{b} = a_1 \times b_1 + a_2 \times b_2 \\ \vec{a} = (a_1,a_2), \vec{b} = (b_1, b_2)
内積の値は2つのベクトルがなす角度と紐づけられる \theta
\vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|\cos\theta
縦棒で囲まれた値はノルムと呼ばれ、そのベクトルの大きさを(三平方の定理より)計算される
|\vec{a}| = \sqrt{(a_1^2 + a_2^2)}
ベクトルのなす角度が計算できると何が嬉しいかというと、ベクトルの向きがどれくらい似ているかを"定量的"に計算できることです。つまり、現段階ではどうやるのかはおいておいて、画像・音声・文章等のデータを同じ次元の空間上のベクトルとして表現することが出来れば、ベクトルの向きの類似度という統一的な指標で(しかも計算が非常にシンプル!)それらの類似度を求められてしまうのです。
以下にデータがベクトルとして空間上にプロットされたとして、それらのなす角度のイメージを表現しています。ここで同じTシャツ画像のベクトルのなす角
つまり、Tシャツ同士の類似度が一番大きいということですね!
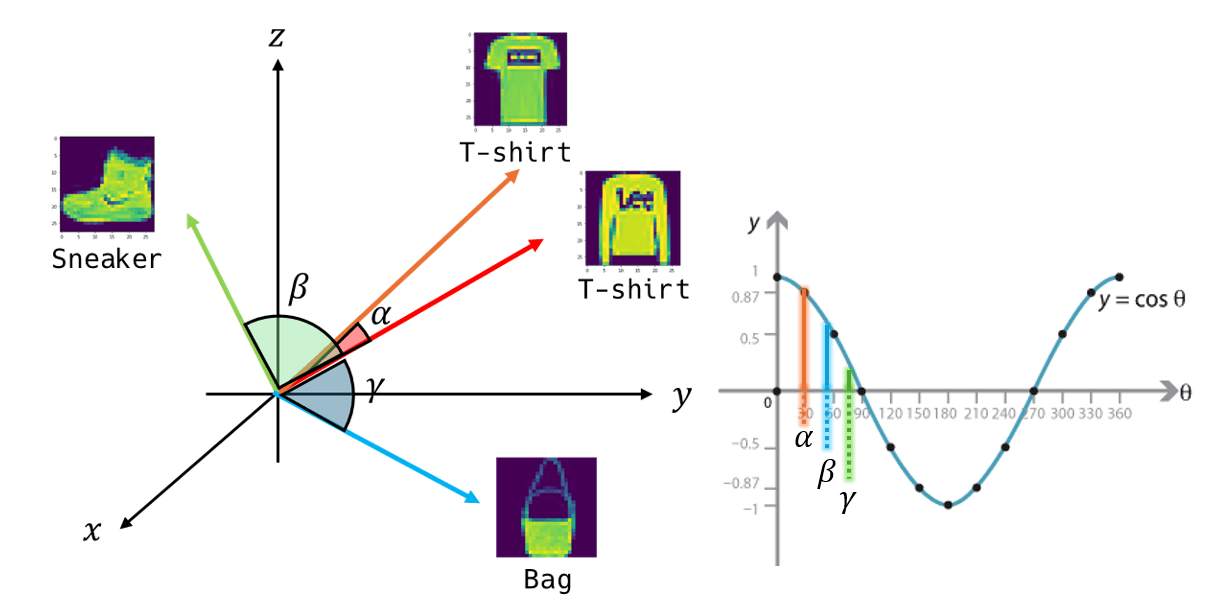
キーワード
文章をベクトルにしたい
これまでの説明で全ての武器は揃いました。
現段階ではどうやるのかはおいておいて、画像・音声・文章等のデータを同じ次元の空間上のベクトルとして表現することが出来れば
という部分について見ていきます。
一応はじめに言葉の定義だけしておきましょう。データをベクトルへ変換することを"エンコード"と呼び、逆にベクトルからデータへ変換することを"デコード"と呼びます。よって、文章をベクトルに変換するアルゴリズムやモデルは一般的に"ベクトルエンコーダー"と呼ばれます。
文章のベクトルエンコーディングの歴史
文章をベクトルとして表現する試みは古く、1970年代以前にまで遡ります。初期の手法として、TF-IDF(Term Frequency-Inverse Document Frequency)があり、これは文書内での単語の出現頻度(TF)と、コーパス全体での希少性(IDF)を組み合わせて、各単語の重要度を評価するものです。
勿論、上記のようなシンプルな方法では文章という非常に複雑なデータを表現するのは難しいでしょう。
大きなブレイクスルーとなったのはニューラルネット技術の黎明期である2013年に発表されたWord2vecと続けて2017年に発表されたTransformerです。現在一般に広く普及しているChatGPTはこのTransformerの系譜であり、GPTのTはTransformerの略だというのは有名な話です。
ここではそれぞれのモデルの動作原理については深入りしませんが本質情報を説明します。Word2vecは"ある単語の周辺単語との共起関係を学習し、単語のベクトル"を表現します。一方でTransformerは"Attention機構により単語間の相互関係を学習し、文章やより大きなかたまりのベクトル"を表現することが出来ます。
以下の項にそれぞれの要点をまとめますが、この記事では各モデルについて深入りはしませんので、各々が気になったモデルについて調べて頂ければと思います。参考として、自分がよく勉強に利用させて頂いているデータサイエンスVTuber アイシアソリッドさんの動画を添えておきます。mm
キーワード
良いベクトル表現に求められる条件とは
ベクトルエンコーダーモデルの動作原理に深入りすると、一気に理解の迷宮に入り込んでしまうため、一旦大前提を明らかにして機械学習理解への道標としましょう。
あるベクトル表現が良いかどうかは、似ているデータ間のベクトルの向きが類似している(なす角度がどれだけ小さいか)ことでしょう。同時に似ていないデータ間のベクトルの向きはできるだけ明後日の方向を向いていて欲しいです。
そのような"良い"空間上では似ているベクトル同士はそれぞれで"集団(クラスタ)"を形成して、それぞれのクラスが極力離れていてくれると嬉しいというわけです。
乱暴な言い方をすれば、ベクトルエンコーダーモデルの学習[1] とは、768次元のような高次元空間上の点に、自由にデータを配置して、上記の制約を満たすような表現=関数を獲得することを意味します。
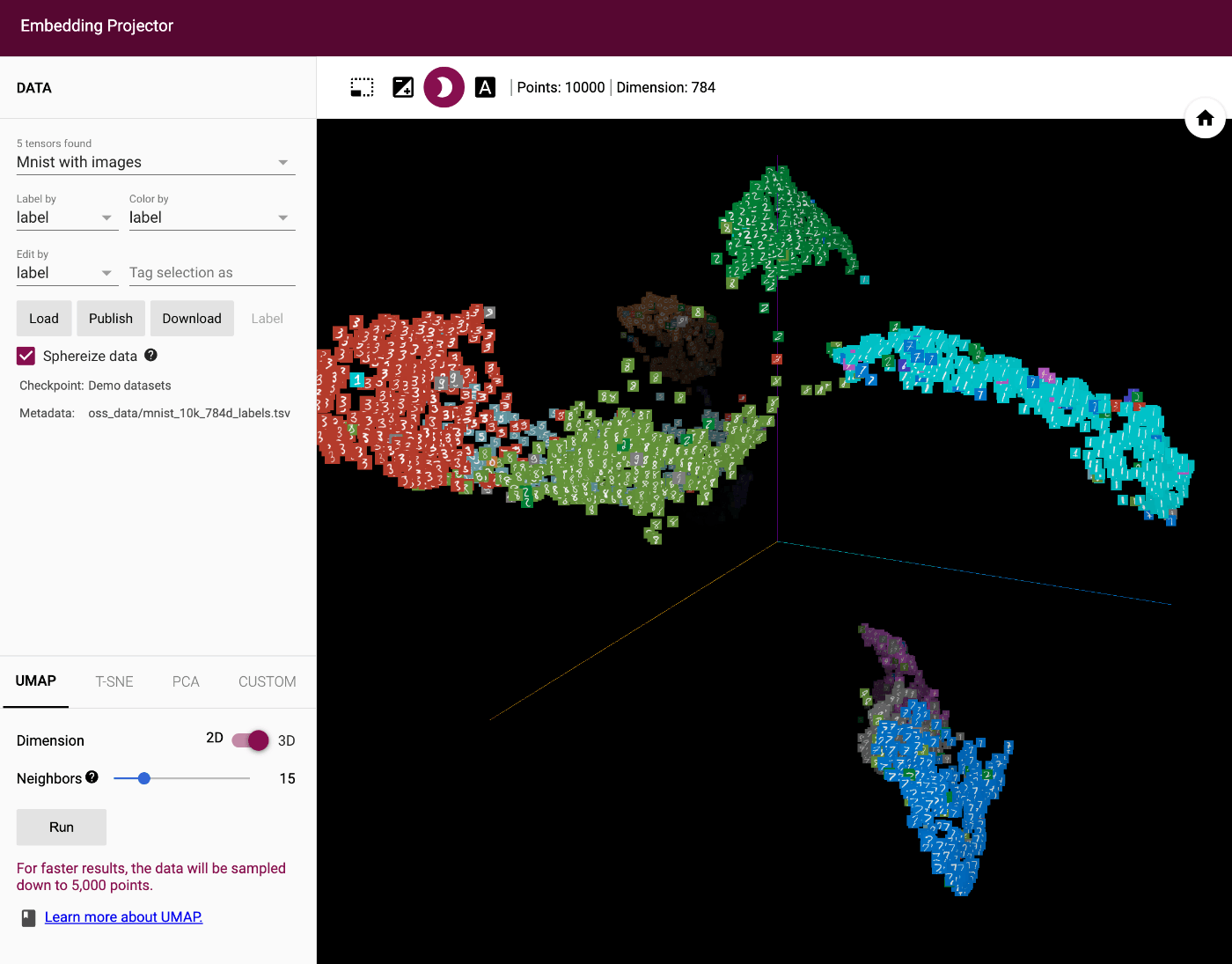
ここで述べていることは以下の2枚の写真が理解の助けになるでしょう。Embedding Projectorでは一般に高次元空間で学習されたデータセットのベクトル表現を"次元削減"[2] というテクニックによって、我々が理解できる平面や空間上にベクトルをプロットした様子を簡単に閲覧できるサービスです。
1枚目の写真はMnistという0から9の手書き数字の画像データを分類するタスクです。
実際に、同じ数字のデータはそれぞれ近くにクラスタを形成しており、違う数字は極力離れているのが見て取れると思います。
2枚目の画像はより今回の題材に近いWord2vecをによる単語のベクトル表現を示しています。一枚絵の都合上上手く映すのが難しいのですが、novelistという職業を表す単語の近くにscientistという単語が来ていたりと、単語の関係をしっかりと獲得できているのが見て取れます。

キーワード・補足
最後に
本記事では、文章や単語をベクトルとして表現することの意義と、その背後にある基本的な概念について解説しました。中学数学程度の知識があれば、機械学習がどのようにして一見魔法のようなタスクを実現し、自然な会話を生成するのか、その原理を感じ取っていただけたのではないでしょうか。
重要なのは、コンピュータが直接扱えるのは数値情報と四則演算のみであるという点です。その制約の中で、いかにして人間が行うような高度な処理を実現するかという技術の集大成が、機械学習の歴史であり、現在のAI技術の礎となっています。
これまでの説明を通じて、ベクトル化の概念やその応用が、日常生活やビジネスの中でどのように活用されているのか、少しでも理解が深まれば幸いです。今後も、機械学習やAIの進化に伴い、これらの技術はさらに身近で重要なものとなっていくでしょう。
また先日の技術同人誌で取り扱った電子ゲームの類似特許権調査に特化したRAGの開発記の記事も近いうちに書きたいです、、、
Discussion