✏️

コーディングテストに必要なアルゴリズムを図でやさしく説明してみた！

2022/08/10に公開

Python

導入

コーディングテストを突破するために、大切なアルゴリズムやデータ構造を解説しています。
この記事では、以下のような人を対象にしています。
実際にアルゴリズムを使って問題を解くところついては、【Python3】コーディングテスト用チートシート（練習問題付き）で紹介していますので、良かったら読んでください。

最低限の数学についての知識がある
使い慣れているプログラミング言語がある
基本的なアルゴリズムを理解している
練習問題を解き慣れている

コーディングテストを受ける前に必要最低限のアルゴリズムを知っておきたい人に向けたもので、
競技プログラミングに参加したい人や、厳密な解説を期待する人に向けたものではないのでご了承ください。

コーディングテストに求められる2つのスキルがあると思います。

コーディングの速度と精度
データ構造やアルゴリズムの理解

この記事では、すべてのアルゴリズムを網羅することや、正確な解説をしていくというよりは、たくさんあるアルゴリズムの中でも、知っておきたいアルゴリズムやデータ構造を図を使ってやさしく解説することを目的としています。

いきなり難しい内容から紹介するのではなく、優しいアルゴリズムから体系立てて説明していくことを意識しました。

1. 二分探索

まずは、有名なアルゴリズムの中でも分かりやすい二分探索と、
アルゴリズムを評価するために必要になるBig O記法について学ぶことにします。

アルゴリズムの魅力に気づくこと、アルゴリズムを評価できるようになることが目標です。

Binary search (二分探索)

my_list = [1, 3, 5, 7, 9] というリストがあるとします。このリストの中に 3 が含まれているのか、もし含まれているならその位置を知りたいとします。具体的には、電話帳からある人の電話番号を知りたいときなどを思い浮かべると良いと思います。

最初に思いつく方法としては、一つずつ見ていく方法です。この方法では、リストに100個の数字が含まれているとすると、最大で100回確認する必要があります。もし、4,000,000,000個の数字が含まれているとすると、最大で4,000,000,000回確認する必要があります。この方法では、入力の大きさに対してアルゴリズムの実行時間が線形になるので、線形時間かかるということがわかります。

二分探索では、中央の値を見て、探している値との大小関係を用いて、探している値が中央の値の右にあるか、左にあるかを判断して、探す範囲を狭めながら見ていく方法です。
my_list = [1, 3, 5, 7, 9] から 3 を探す過程を図にしてみました。

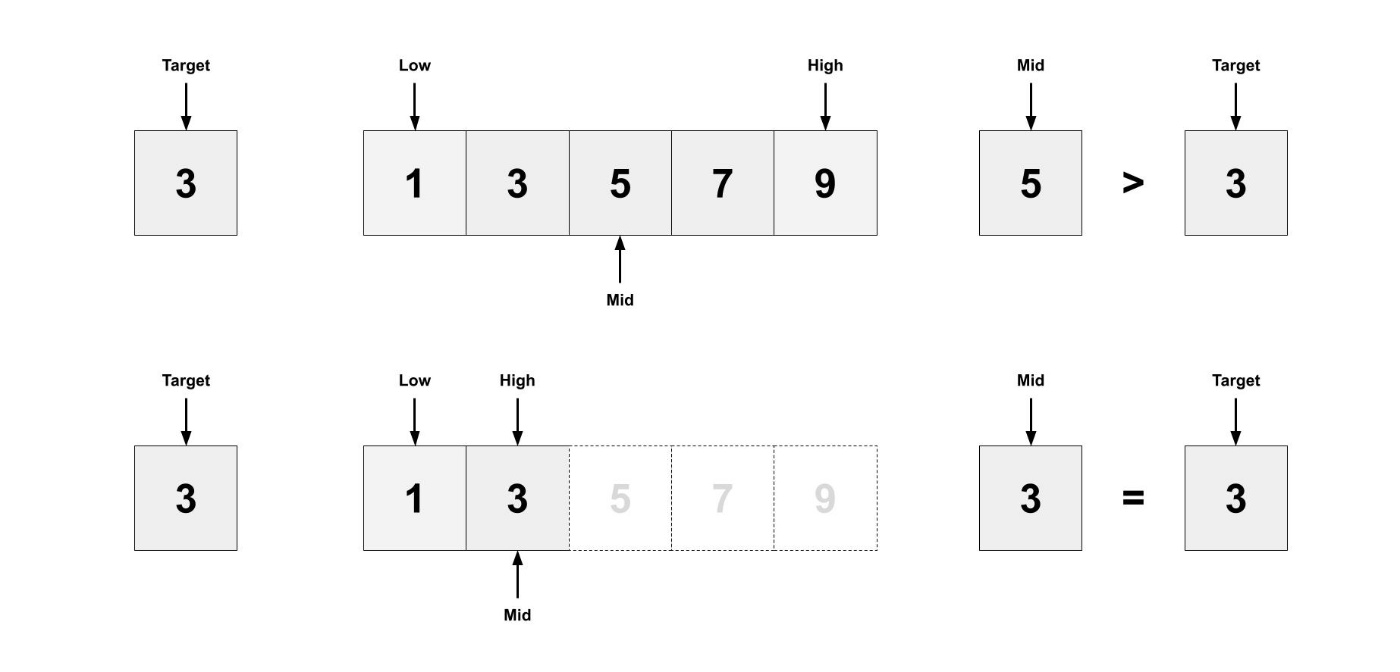
コードを書いて実装すると理解が深まると思います。

def binary_search(list, item):
    low = 0
    high = len(list)-1
    
    while low <= high:
        mid = (low + high) // 2
        guess = list[mid]
        if guess == item:
            return mid
        if guess > item:
            high = mid - 1
        else:
            low = mid + 1
    return None

二分探索を使うと、どのくらい時間が節約できるのでしょうか？
リストに100個の数字が含まれているとすると、最大で7回確認する必要があります。もし、4,000,000,000個ならの数字が含まれているとすると、最大で32回確認する必要があります。この方法では、対数時間かかるということがわかります。

Big O記法

Big O記法は、アルゴリズムがどのくらい速いかを表すための記法です。アルゴリズムを比較するときに一番簡単な方法は実行時間を比較することですが、線形時間で実行されるアルゴリズムと、対数時間で実行されるアルゴリズムでは、リストのサイズが大きくなるにつれて実行時間の差が開きます。 そこで、Big Oでは秒単位の速さではなく、演算回数を比較することが目的となっています。

演算回数の前に「大文字のO」をつけるので、Big O記法と呼ばれています。

一つずつ見ていく方法と二分探索を使う方法での時間計算量を考えてみましょう。
$n$ 個のデータがある場合で、それぞれの時間計算量をBig O記法で表すと以下のようになります。

アルゴリズム	時間計算量
一つずつ見ていく方法	$O(n)$
二分探索	$O(\log _{2}n)$

Big O記法は、アルゴリズムがどのくらい速いかを表すための記法と言いましたが、正確には最悪のケースでの実行時間を表しています。一つずつ見ていく方法で my_list = [1, 3, 5, 7, 9] の中から 1 を探すとすると、すべての項目を見る必要がなく一発で見つけられるため $O(1)$ とも考えられます。逆に 9 を探すとすると、すべての項目を見る必要があり $O(n)$ となります。Big O記法では、このアルゴリズムがこれより遅くなることはない最悪のケースを表しています。

もちろん最悪のケースの実行時間だけでなく、平均のケースの実行時間を考えることも重要です。

よく見るBig O記法の時間計算量を紹介します。

$O(\log n)$ : 二分探索
$O(n)$ : 一つずつ見ていく方法
$O(n * log n)$ : クイックソート
$O(n^2)$ : 選択ソート
$O(n!)$ : 巡回セールスマン問題

2. 選択ソート

基本的なデータ構造である配列と連結リストを紹介して、データ構造の特性を学びます。
また、要素を並び替えるために使う、ソートアルゴリズムを学びます。

データ構造を意識すること、どのソートアルゴリズムを使うか考えられることが目標です。

配列と連結リスト

Pythonでよく使う my_list = [1, 3, 5, 7, 9] は、配列というデータ構造です。
データ構造としての特徴は、何番目にどの要素があるかという情報を保持している点です。

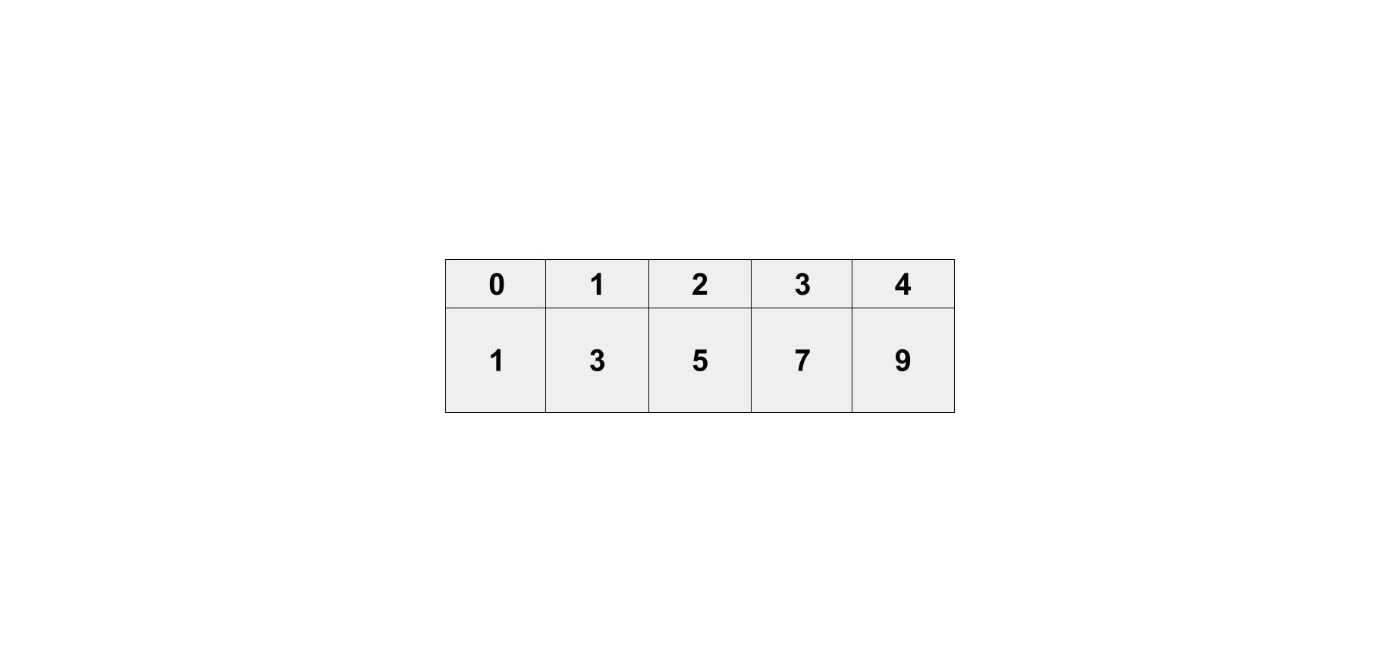
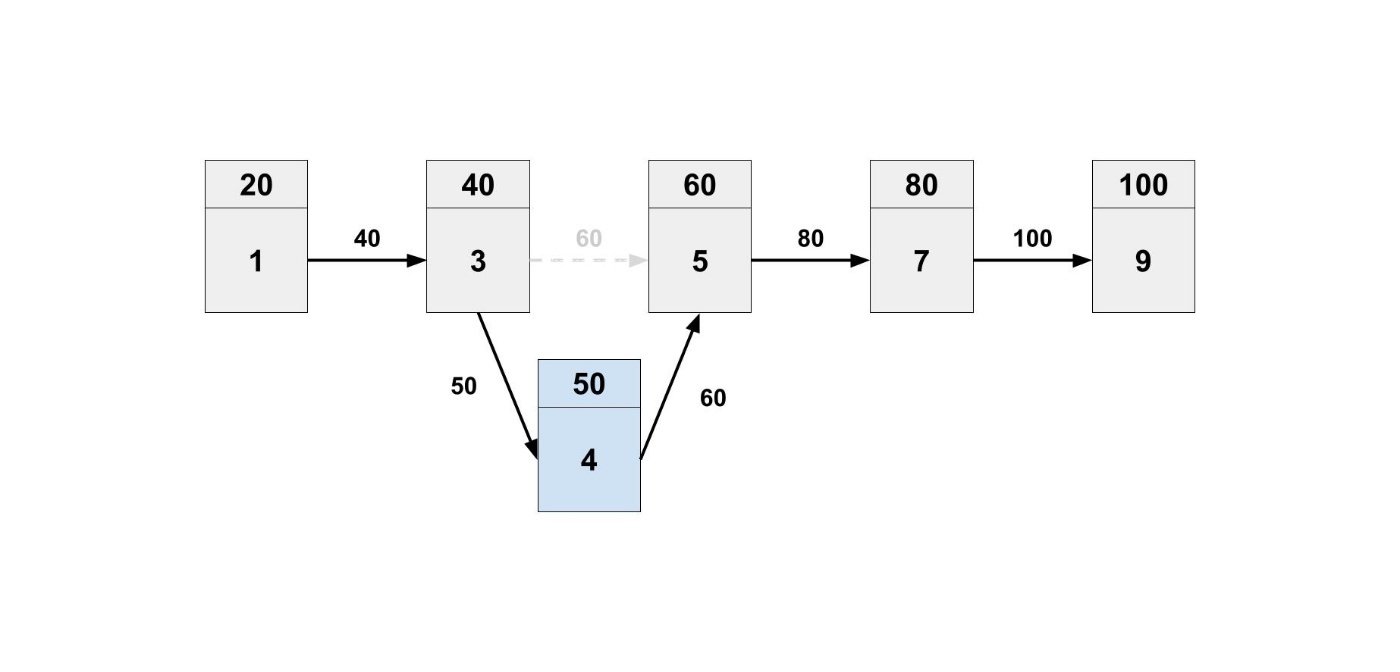
連結リストは、要素と次のデータの場所からなるデータ構造です。
これは、図を見た方が理解できると思います。
1つ目の要素は 1 であり、次のデータの場所 40 という情報を持っています。
2つ目の要素は 40 という場所に行けば 3 だと確認できます。

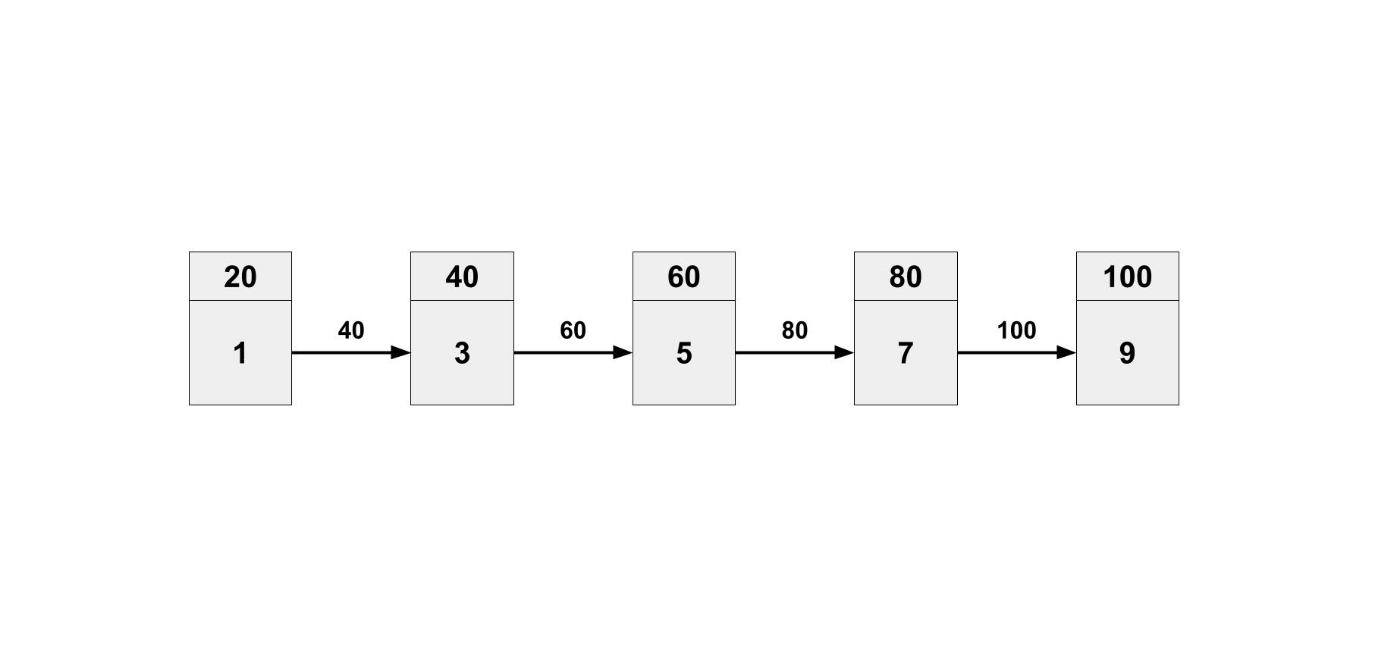
よくある実装としては、以下のようなものがあります。

class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

配列と連結リストはどちらも複数の要素を格納するためのデータ構造です。
しかし、それぞれ得意なこと、苦手なことがあります。

配列と連結リストの比較

操作内容	配列	連結リスト
データアクセス	$O(1)$	$O(n)$
データ挿入・削除	$O(n)$	$O(1)$

例えば、3番目の要素にアクセスしたいとします。
配列は、何番目に何があるか分かるので、いきなり3番目の要素にアクセスすることができます。
連結リストは、先頭から一つずつたどっていく必要があります。

例えば、2番目に要素を追加したいとします。
配列は、何番目に何があるか分かるようにしないといけませんでした。
要素を追加したときに、もともとあった要素たちをずらす作業が必要になります。

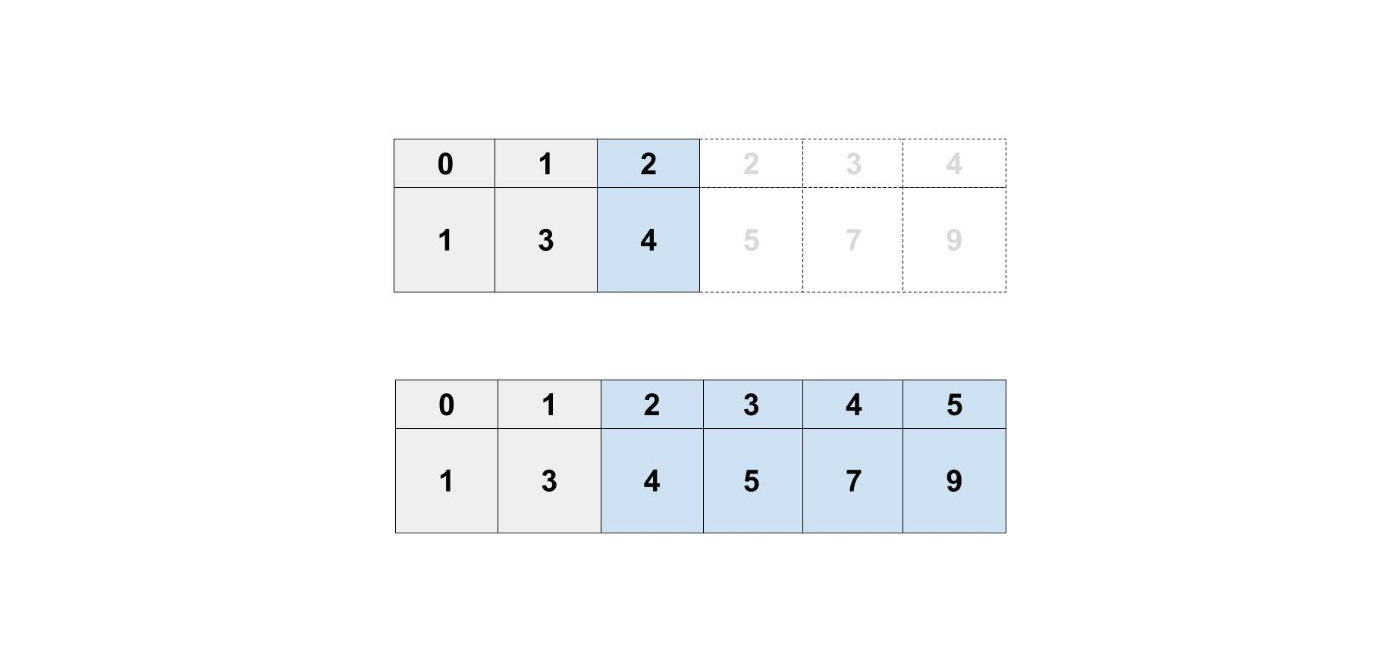
連結リストは、次のデータの場所しか持っていないので、他の要素への影響がありません。

Selection Sort (選択ソート)

ここで、基本的なアルゴリズムである選択ソートを学びたいと思います。
データを昇順、降順など、一定の規則に従って整列させることがあります。
そのときに必要になるのが、ソートアルゴリズムです。
ソートアルゴリズムにはいくつか種類があり、それぞれの特徴を知ることが大切です。

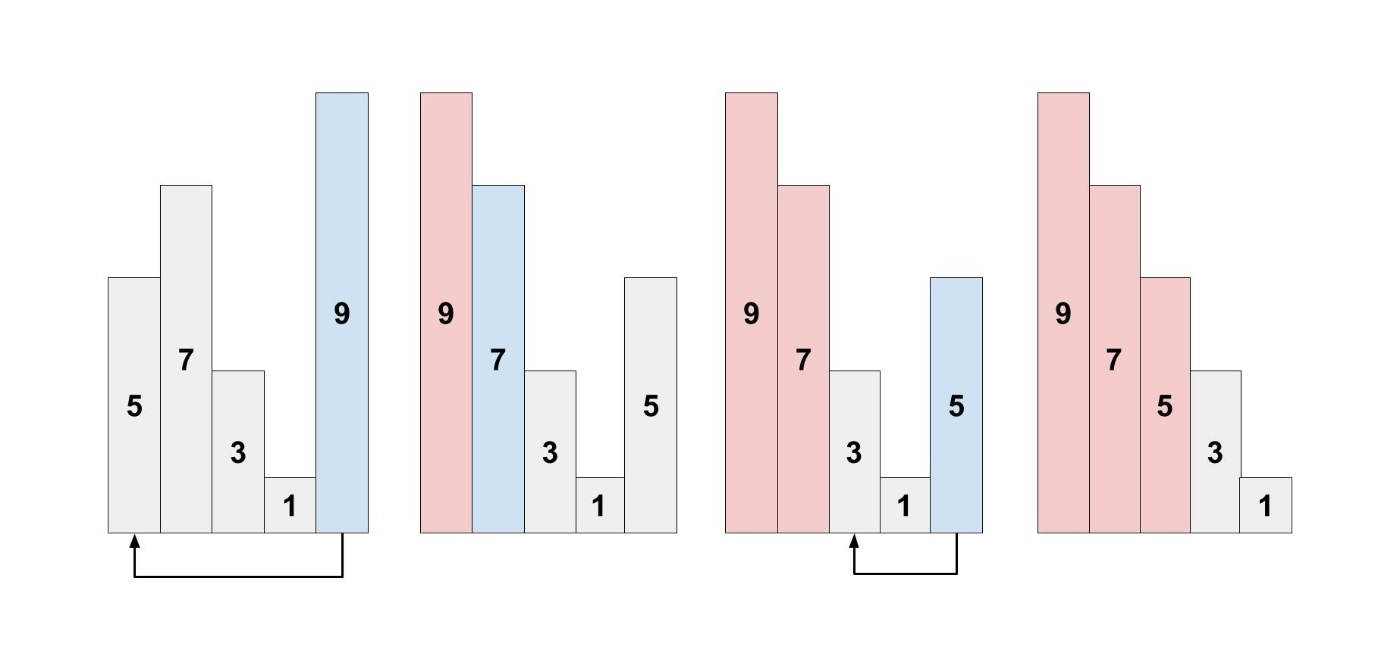
選択ソートでは、配列の中から最大値を見つけ出して、一番目の要素と入れ替えます。
次に、配列の二番目以降から最大値を見つけ出して、二番目の要素と入れ替えます。
これを繰り返すことで、配列を並び替えることができます。

ここで、Big O記法を用いて時間計算量を考えたいと思います。
まず、要素が $n$ 個ある配列の中から最大値を見つけ出すには、 $n$ 回比較する必要があります。
そして、配列の先頭から最後までこの作業 $n$ 回を繰り返す必要があります。
よって、時間計算量は $O(n^2)$ となります。

$O(\frac{1}{2} * n^2)$ ではないのかと思われるかもしれないですが、Big O記法では計算量がどのように増加するかが重要なので、定数は無視することが一般的です。

コードを書いて実装すると理解が深まると思います。

def findSmallest(arr):
     smallest = arr[0]
     smallest_index = 0
     for i in range(1, len(arr)):
         if arr[i] < smallest:
             smallest = arr[i]
             smallest_index = i
     return smallest_index
     
def selectionSort(arr):
     sorted_arr = []
     for i in range(len(arr)):
         smallest_index = findSmallest(arr)
         sorted_arr.append(arr.pop(smallest_index))
     return sorted_arr

3. 再帰

少し難易度は上がりますが、再帰とスタックについて学んでいきます。
再帰関数を使ってみること、スタックを理解することが目標です。

Recursion (再帰)

フィボナッチ数列というものを知っていますか？

フィボナッチ数列は、次の漸化式で定義されます。
$F_0 = 0$
$F_1 = 1$
$F_{n+2} = F_n + F_{n+1}$ $(n\geq0)$

第0項から第11項の値は次の通りです。

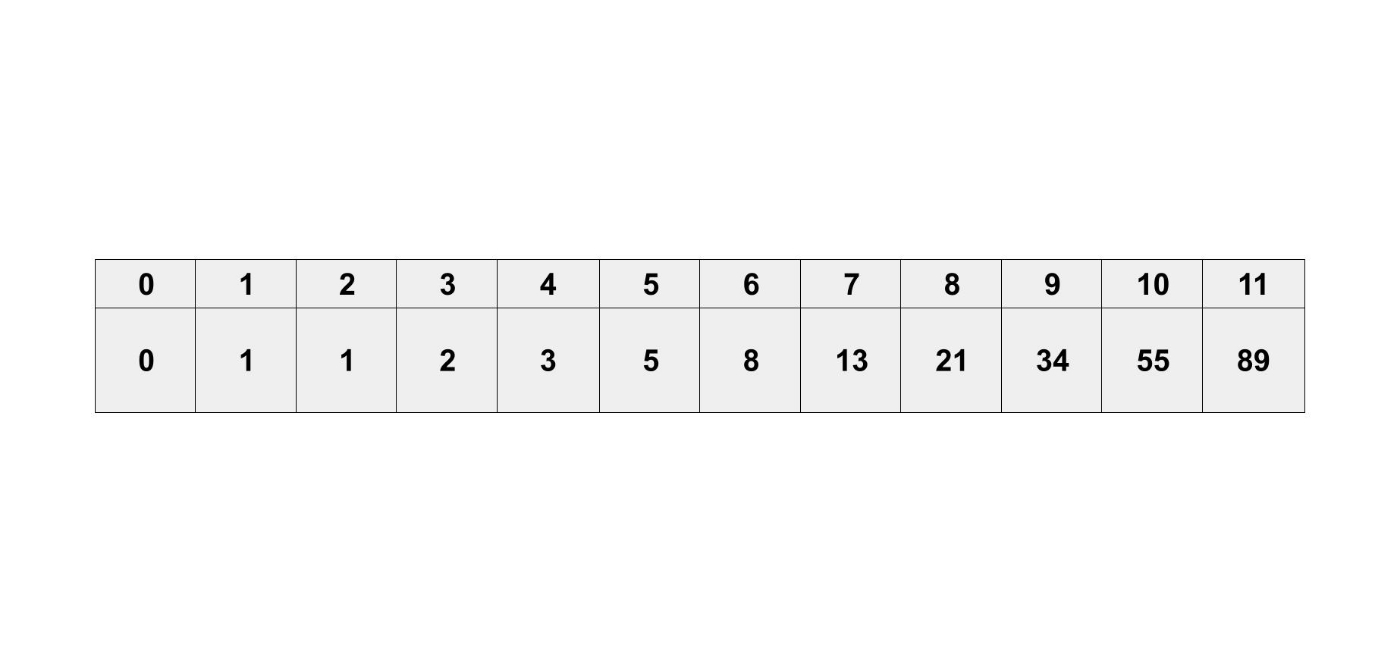
簡単に言えば、一つ前の値と、今の値を足したものが、次の値になっています。
例えば、第4項の値は、第2項の 1 と第3項の 2 を足した 3 となっています。

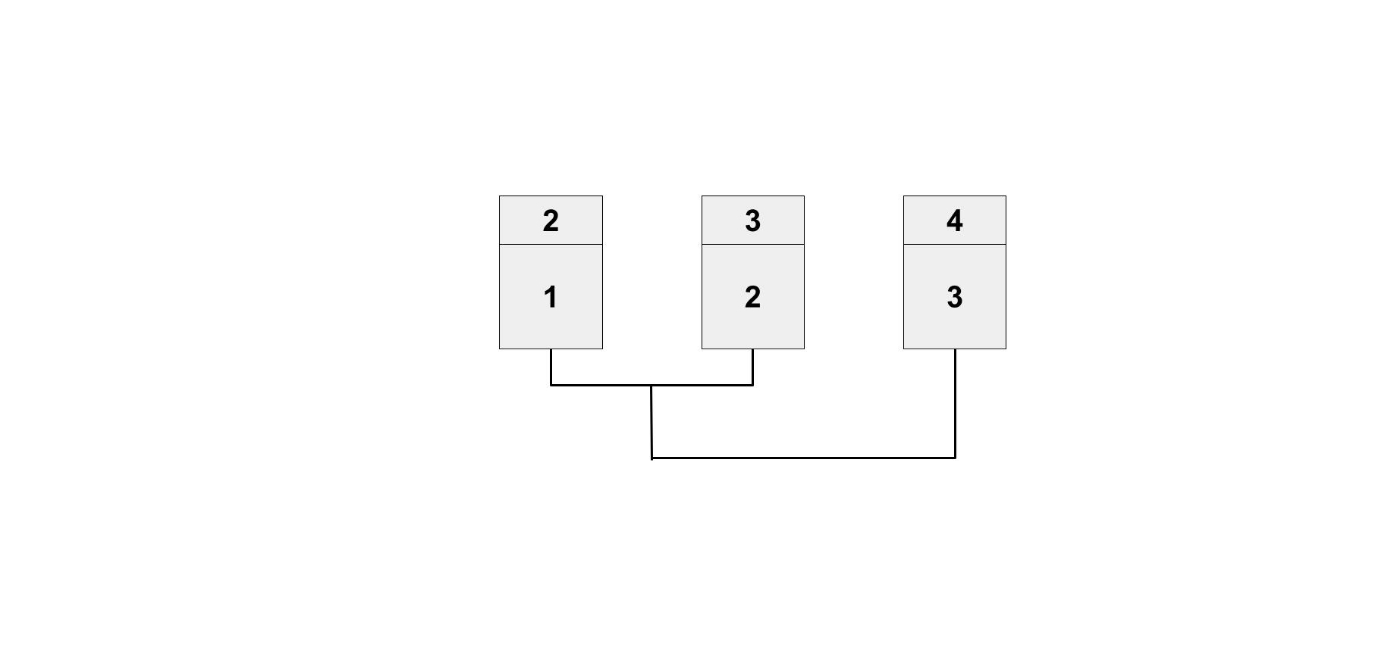
フィボナッチ数列の第 $n$ 項の値を、再帰を使って求めましょう。
再帰とは、ある関数が自分自身を呼び出すことです。

def fibonacci(n):
    if n == 0 or n == 1:
        return n
    else:
        return fibonacci(n-1) + fibonacci(n-2)

具体的に数字を入れて考えてみると分かりやすいと思います。
fibonacci(4) を計算すると以下の図のようになります。

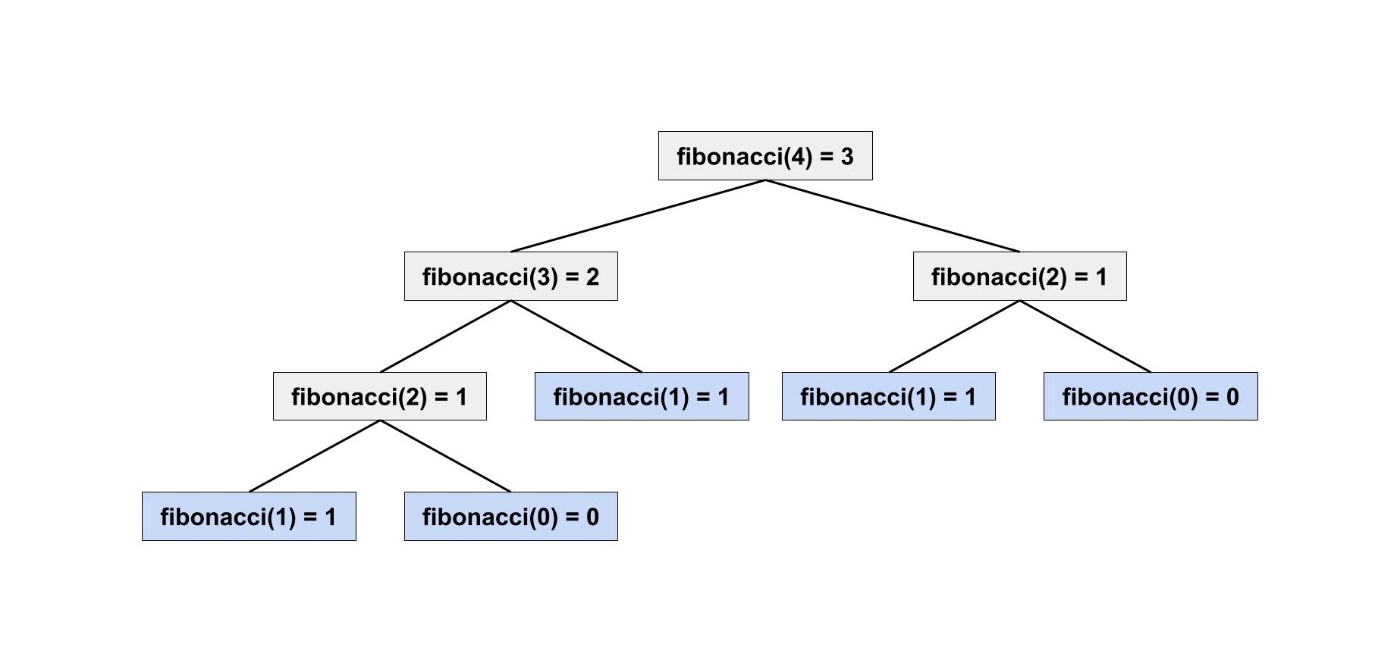
数学の定義をそのままコードにすることで、本当に求めたい値が求められました。
このように再帰を使うことで、解決策を明確に示すことができるのです。

再帰関数には、ベースケースという処理が必要になります。
上図では n = 0 と n = 1 がベースケースで青色になっています。
再帰関数を呼び出すと、再帰していく中で、必ずベースケースに到達します。
ベースケースがないと、永遠に再帰してしまい無限ループになるので注意しましょう。

実は、再帰を使うことに性能上の利点はあまりありません。
むしろ、ループの方が性能的に優れていることも多いです。

例えば、フィボナッチ数列の第 $n$ 項の値を、ループ使って求めてみましょう。
こちらの方が性能としては、優れていますが、再帰を使った方が直感的に理解できると思います。

def fibonacci(n):
    a, b = 1, 0
    for _ in range(n):
        a, b = b, a + b
    return b

再帰関数の仕組みを理解するために重要なスタックというものがあります。

Stack (スタック)

スタックと聞くと難しそうに感じるかもしれませんが、仕組みは簡単です。
スタックは、基本的なデータ構造の1つで、後に入れたものが先に出る構造になっています。

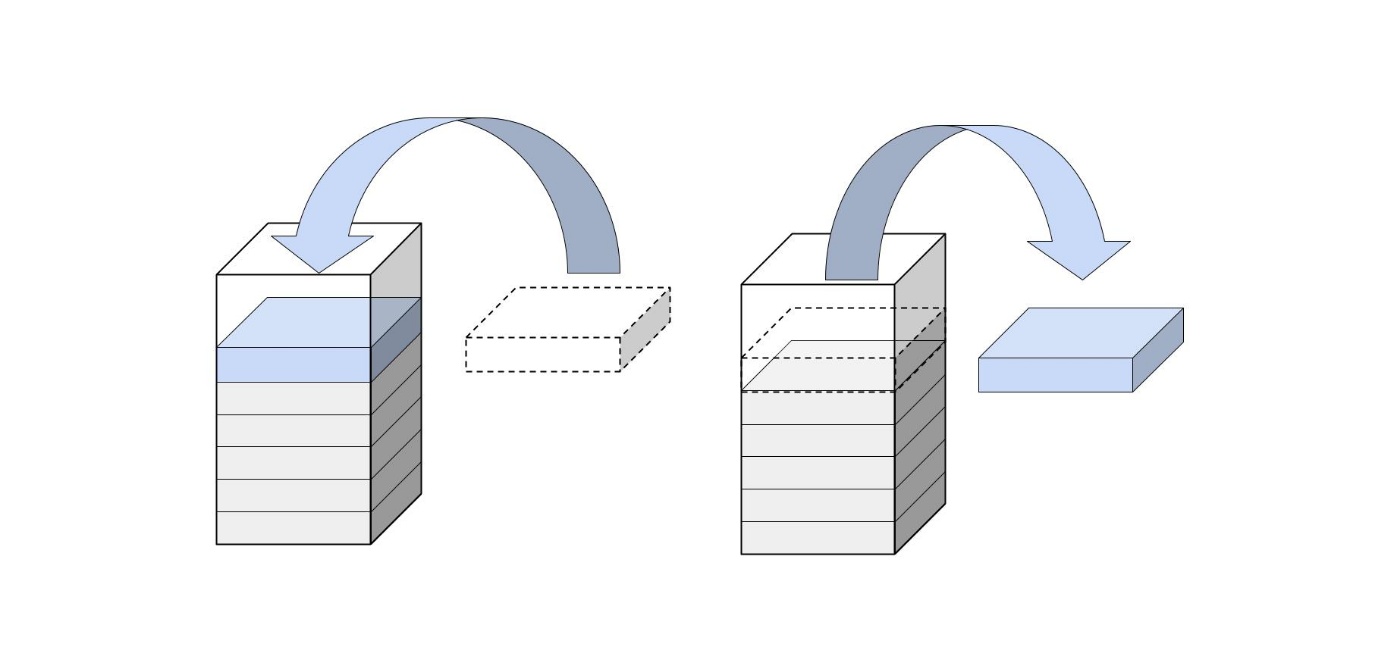
プログラムでもコールスタックという呼ばれるスタックが使われています。
すべての関数呼び出しは、コールスタックに入ります。

fibonacci(4)の例で考えてみましょう。
fibonacci(4)を解くためにfibonacci(3)やfibonacci(2)を解く必要があります。
そうすると実行中の関数がコールスタックに入っていきます。

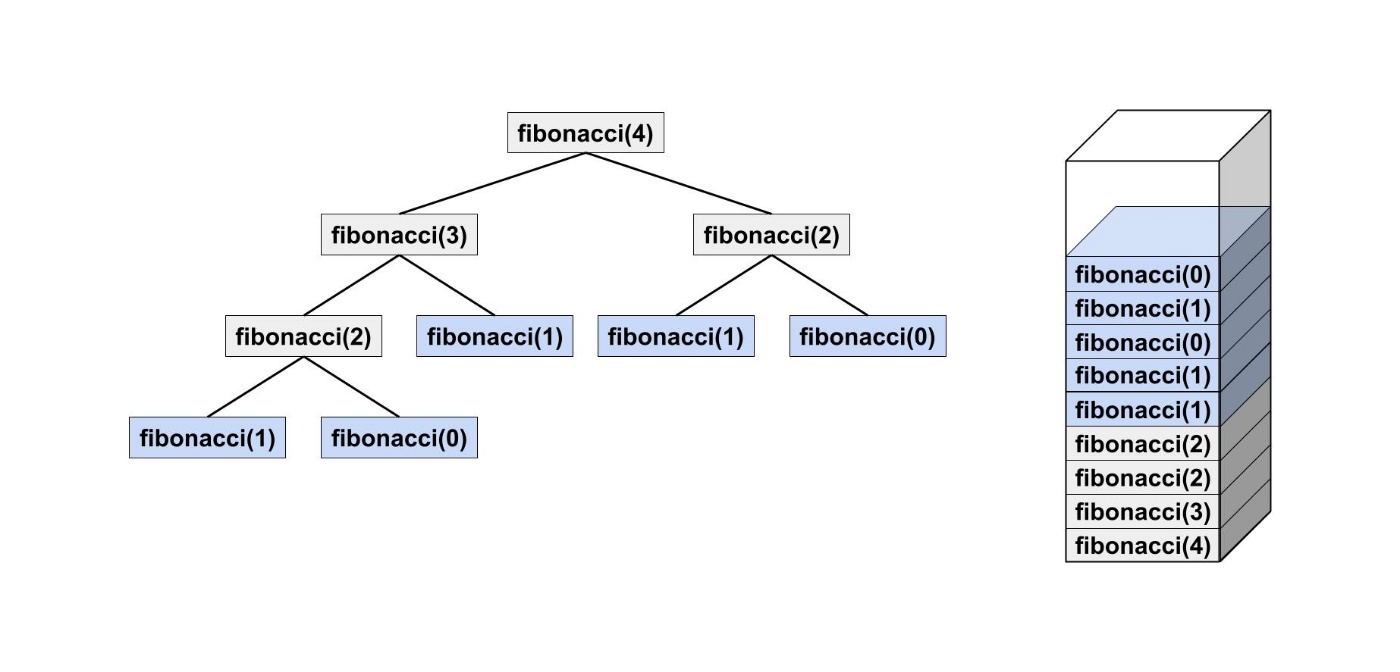
コールスタックは非常に大きくなる可能性があり、多くのメモリを消費します。
スタック用のメモリが不足してしまうことを Stack Overflow と言います。
どこかで聞いたことがある言葉ですね。

「再帰を使わないで、ループを使った方がいいのではないか？」と思われるかもしれません。
しかし、ループに負けない再帰の方法として、末尾再帰というものがあります。
再帰の弱点として、コールスタックは非常に大きくなるという問題がありました。
fibonacci関数を末尾再帰にするには、そこまで計算した途中結果を引数に渡す必要があります。

4. クイックソート

問題を解く能力を上げるために、分割統治法とクイックソートについて学びます。
分割統治法を知ること、クイックソートが優れている理由を理解することが目標です。

分割統治法

いろいろなアルゴリズムを学ぶと、問題を解くときにどのアルゴリズムで解くか考えると思います。
残念ながら、どのアルゴリズムでも解けそうにない問題に出会う可能性があります。
そうしたときに、使うテクニックの一つが分割統治法です。
他には、動的計画法、貪欲アルゴリズム、などがあります。

分割統治法は、難しい問題を解く方法の一つで、問題全体を同じ構造の小さな問題に分割して、簡単に解けるサイズにしてから解いていく方法です。

分割する: 再帰を利用して、問題を小さな問題に分割します。
小さな問題を解く: 小さな問題を再帰的に解いていきます。十分小さくなったところで直接解きます。
結合する: 小さな問題の部分的な解を結合して、問題全体を解きます。

普段の生活で分割統治法を使っている例を考えてました。
足し算するときに、分割してから足し合わせる方法を使ったことがあるのではないでしょうか？

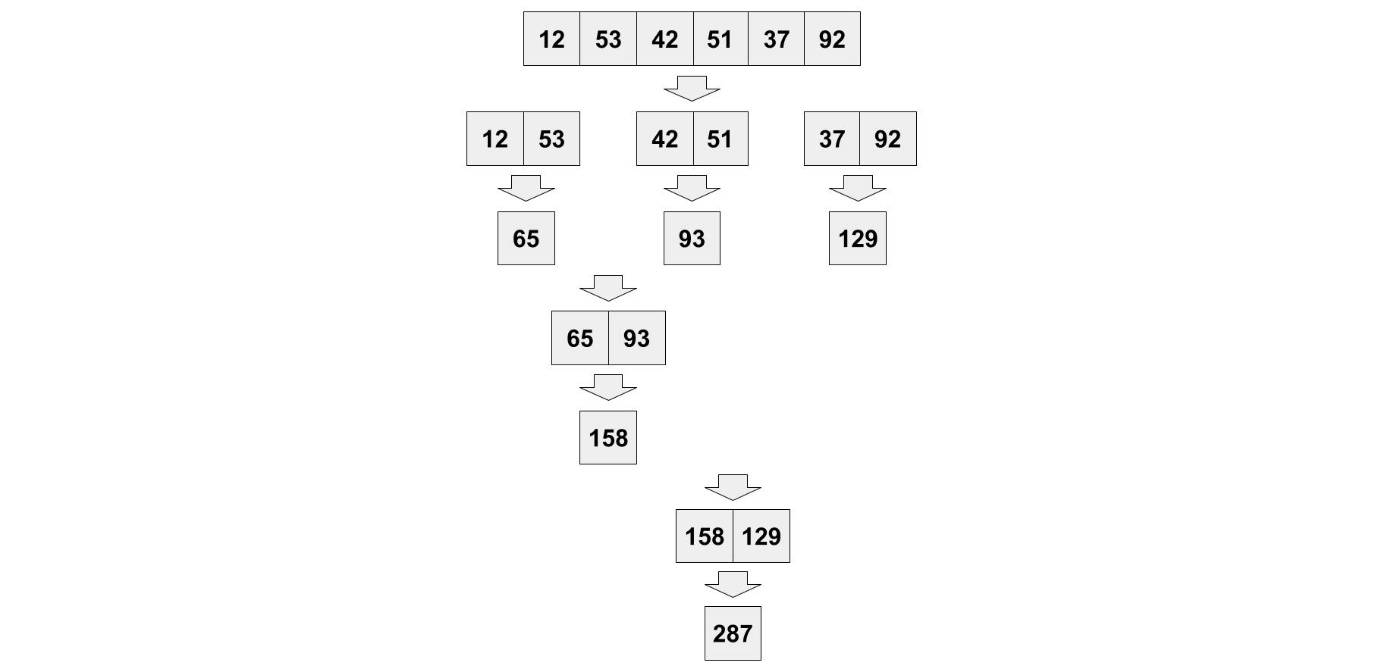
Quicksort (クイックソート)

クイックソートは、実際によく使われる優れたソートアルゴリズムです。
そんなクイックソートは分割統治法を使っています。

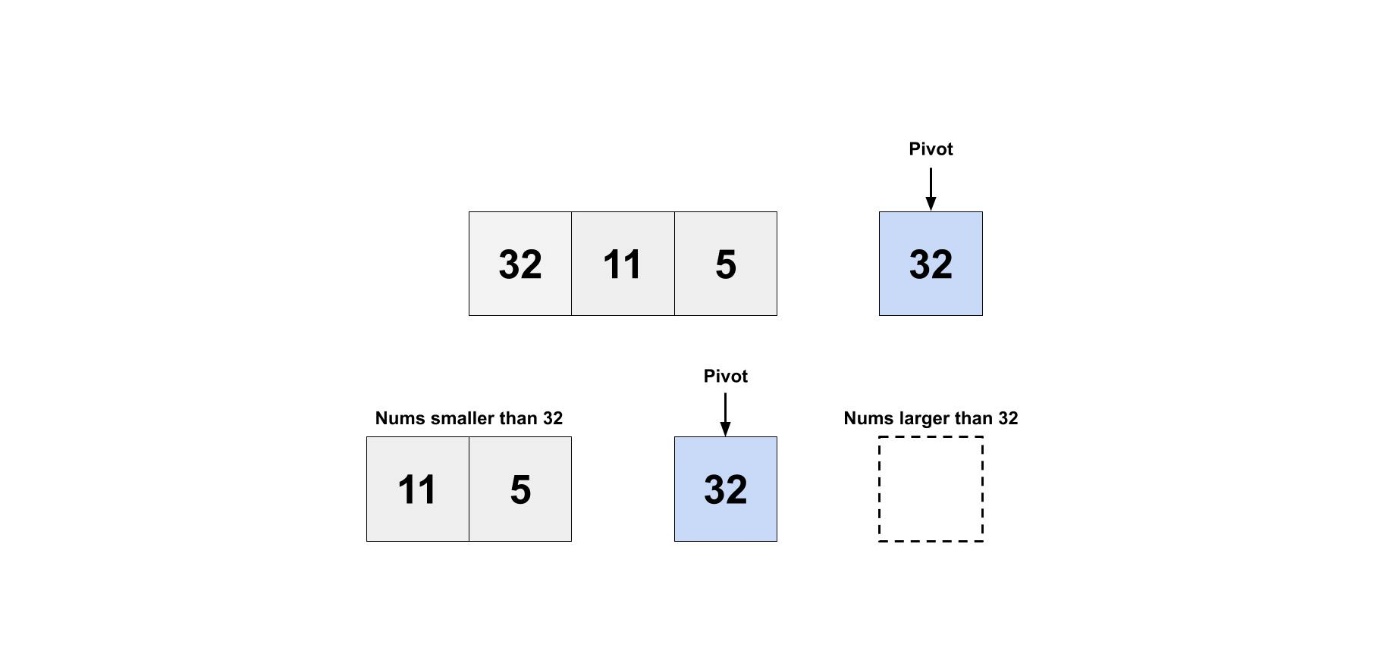
クイックソートでは、あるデータの中からランダムな要素をpivot(ピボット)として選択します。
ピボットより小さいグループと、ピボットより大きいグループの2つに振り分けます。
これをグループが空になるか、要素が一つだけになるまで繰り返します。
その後、小さいグループ、ピボット、大きいグループを結合して、ソートされた配列を得られます。

コードを書いて実装すると理解が深まると思います。
実際によく使われる優れたソートアルゴリズムですが、簡単に実装することができます。

def quicksort(array):
    if len(array) < 2:
        return array
    else:
        pivot = array[0]
        less = [i for i in array[1:] if i <= pivot]
        greater = [i for i in array[1:] if i > pivot]
        return quicksort(less) + [pivot] + quicksort(greater)

今までのアルゴリズムと同様に、Big O記法でアルゴリズムの評価していきましょう。
と言いたいところですが、クイックソートは、選択するピボットによって速度が変わります。
もし非常に悪いピボットの選び方をすると時間計算量は $O(n^2)$ になります。
最悪のケースでの実行時間だけを考えると、選択ソートと変わりません。
クイックソートが、優れたアルゴリズムである理由は、平均のケースの実行時間にあります。
クイックソートの平均実行時間は $O(n * log n)$ です。

ソートアルゴリズムを比較するときにおすすめサイトを紹介しておきます。

Sorting Algorithms Animations

マージソートと呼ばれるソートアルゴリズムがありますが、最悪のケースでも $O(n * log n)$ です。
なぜ、マージソートを使わないのでしょうか？
選択ソートの $O(n^2)$ とクイックソートの $O(n * log n)$ を比較するときに、
選択ソートの定数を考慮して $O(\frac{1}{2} * n^2)$ としても、特に影響がありません。
しかし、マージソートと比較するときに、定数の影響がないと言えるのでしょうか？

5. ハッシュテーブル

最強のデータ構造の一つであるハッシュテーブルについて学びます。
ハッシュテーブルは、基本的なデータ構造の中でも非常に強力です。
とは言え、もう既にハッシュテーブルを使っている人の方が多いと思います。
そこで、ハッシュテーブルの仕組みを理解することが目標です。

ハッシュテーブルは、コーディングテストのアドバイスで、「とりあえずハッシュテーブルを使えばどうにかなる」という冗談があるほど強力です。コーディングテストに挑むときには、ハッシュテーブルは必ず候補になります。ハッシュテーブルが使えないなら、グラフ構造にならないかといった感じです。

ハッシュ関数

ポケモン図鑑からあるポケモンのタイプを知りたいとします。
もし、ポケモン図鑑が名前順になっていないと、一つずつ確認していくしかありません。
時間計算量は $O(n)$ となってしまい、一体調べるのに時間がかかってしまいます。
ポケモン図鑑が名前順になっていれば、二分探索を使うことができます。
時間計算量は $O(\log n)$ となり、だいぶ時間を短縮できました。
しかし、それでもポケモンのタイプを調べるのが面倒になってくると思います。

そこで必要になるのが、ポケモンに詳しい友達です。
ポケモンに詳しい友達は、ポケモンの名前とタイプをすべて記憶しています。
そんな友達がいれば、いちいち図鑑を見なくても一瞬で答えが返ってきます。
時間計算量は $O(1)$ となり、二分探索を使うよりも時間を短縮できます。

ここで、ポケモンに詳しい友達の代わりになるようなデータ構造が欲しくなります。
そんな夢のようなデータ構造はハッシュ関数と配列を組み合わせることで実現できます。

ハッシュ関数は、文字列を入れると数値が返ってくる関数です。
ただし、ハッシュ関数にはいくつかの要件があります。

一貫性があること
異なる文字列を異なる数値に対応させなければならないこと

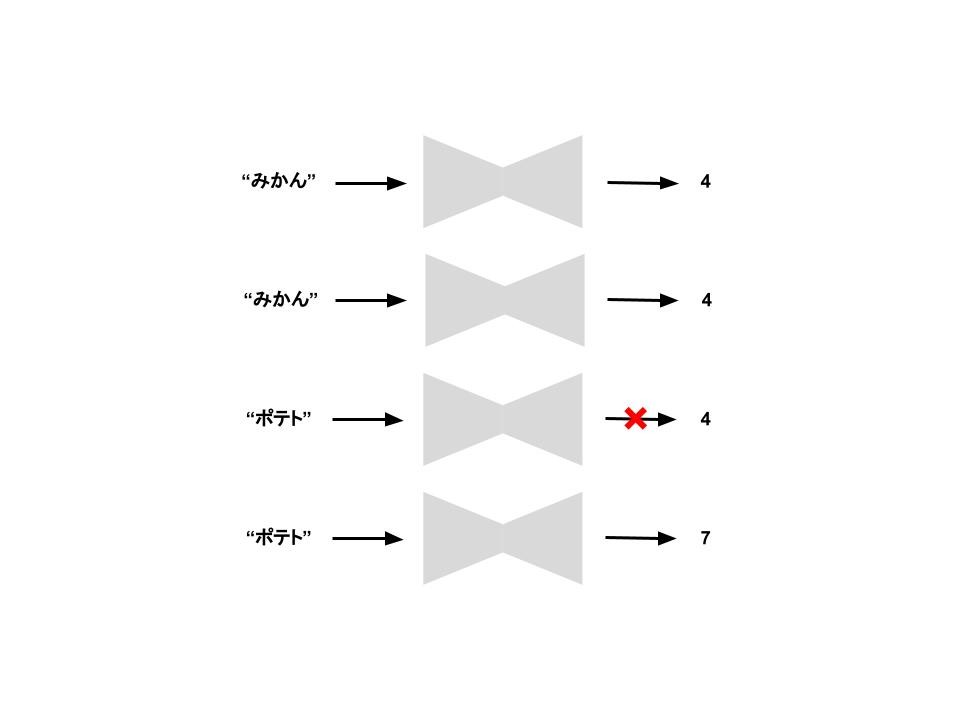
「みかん」という単語を入れると「4」が返ってくるとします。
もう一度「みかん」という単語を入れたときに、ちゃんと「4」が返ってくる必要があります。
このように一貫性があることがハッシュ関数には必要です。

ここで、「ポテト」という単語を入れたときに、「4」が返ってきてしまうと問題があります。
どんな単語を入れても必ず「4」を返すのでは意味がありません。
異なる文字列を異なる数値に対応させなければならないことがハッシュ関数には必要です。

Hash Tables (ハッシュテーブル)

ポケモンに詳しい友達の代わりになるデータ構造を作るために、ハッシュ関数に関して学びました。
そんな夢のようなデータ構造は ハッシュテーブル といいます。
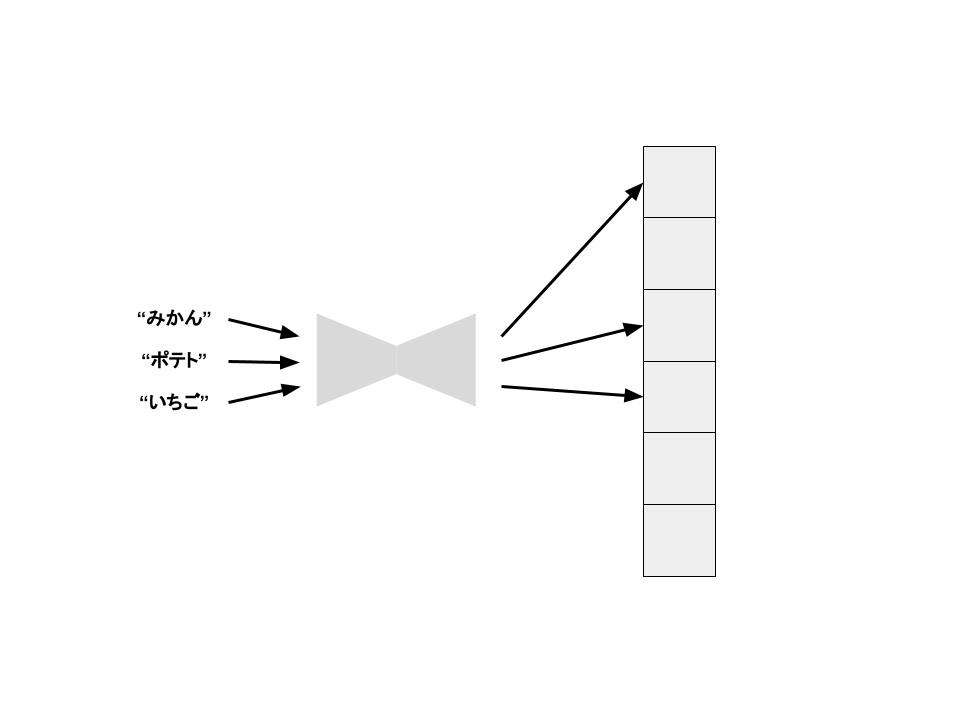
ハッシュテーブルはハッシュ関数と配列を組み合わせることで実現できます。

「みかん」という単語を入れると「4」が返ってきました。ここで「みかん」の値段を用意しておいた配列の4番目の位置に格納しておくことができます。「ポテト」という単語を入れたときは「7」が返ってきました。同様にして「ポテト」の値段を配列の7番目の位置に格納できます。

ここで「みかん」の値段を知りたいとします。
ハッシュ関数の特性として、もう一度「みかん」を渡せばちゃんと「4」が返ってくるので、配列の4番目の位置を確認しにいくだけで、「みかん」の値段を知ることができるのです。

ハッシュテーブルを使えば、検索する必要はまったくないのです。
ハッシュテーブルは、おそらく、これから学ぶ複雑なデータ構造の中で最も有用なものです。
Pythonでは、ハッシュテーブルは辞書として実装されています。
d = {'mikan': 400, 'potato': 300}

ハッシュテーブルの実装は複雑なので、ここでは紹介しません。
ハッシュテーブルの実装が気になる方は、調べてみてください！

常に異なる入力に対して、配列の異なる位置に対応させるというのは、可能なのでしょうか？
出来るだけそのようなことが起きないよなハッシュ関数を使っています。
しかし、同じ位置に割り当ててしまう「衝突」が起きてしまうことがあります。

6. 幅優先探索

ネットワークをモデル化するためのデータ構造であるグラフを紹介します。
また、グラフ上で実行できる強力なアルゴリズムである幅優先探索を学びます。
幅優先探索は、最短距離を求めることができます。

家から学校まで行くのに、どの経路で行くと早いか考えたことがありませんか？
このような問題を 最短経路問題 といいます。
他にも、チェスでチェックメイトするまでの最短の手数も最短経路問題として扱えたりします。

この最短経路問題を解くアルゴリズムは、幅優先探索と呼ばれます。
最短経路問題を解くには、以下の手順で行う必要があります。

問題をグラフとして扱う
幅優先探索を利用する

グラフとは?

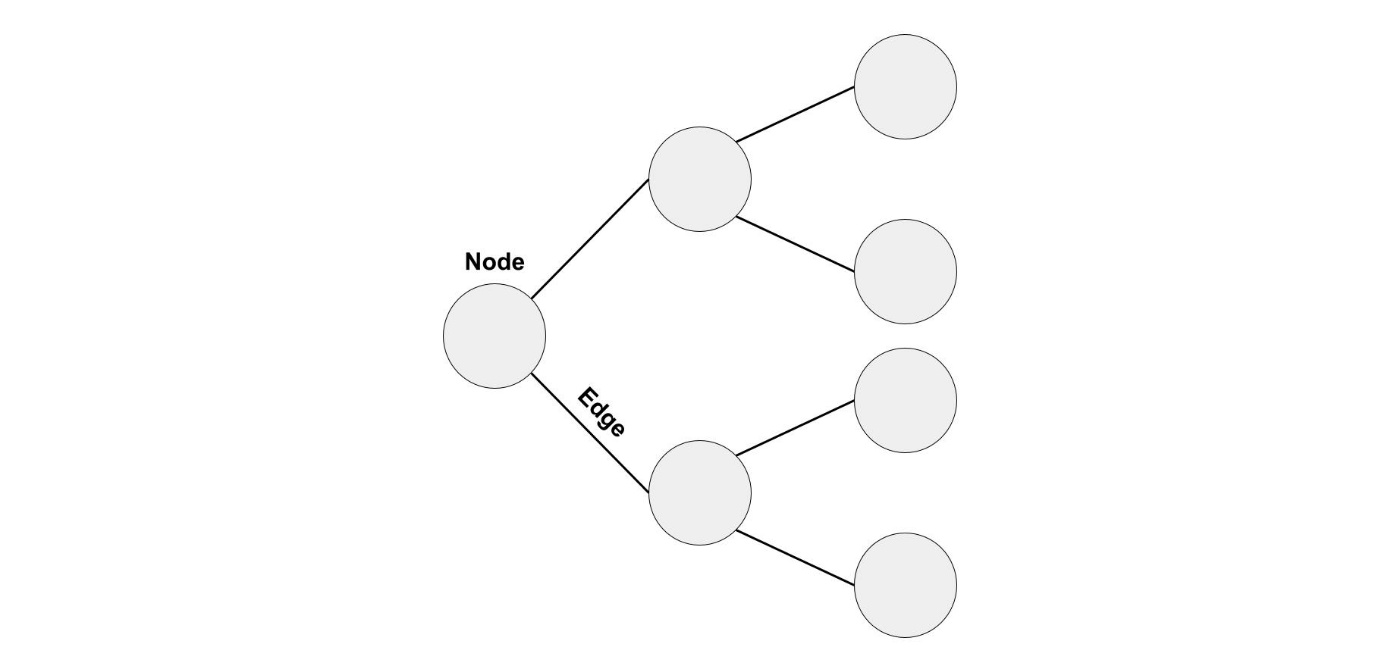
グラフは、さまざまなものが互いにどのようにつながっているかをモデル化する方法です。
グラフは、ノードとエッジで構成されています。

Breadth-first search (幅優先探索)

探索アルゴリズムは、複数のデータの中からある値を見つけるために用いられます。
今まで紹介したアルゴリズムの中では、二分探索が探索アルゴリズムです。
幅優先探索は、グラフ上で実行できる種類の探索アルゴリズムです。

コーディングテストでは、幅優先探索で解けるタイプの問題があります。
ある場所からある場所へ行くための経路はあるか？
ある場所からある場所へ行くための最短経路は何か？

以下のような迷宮があるとします。
一つのマスが道になっており、青色のマスは通ることができません。
S(スタート)からG(ゴール)に、最短何マスで行くことができるか考えたいと思います。
あるマスからは移動できるのは、左右上下のマスのみで、斜めに移動することができません。

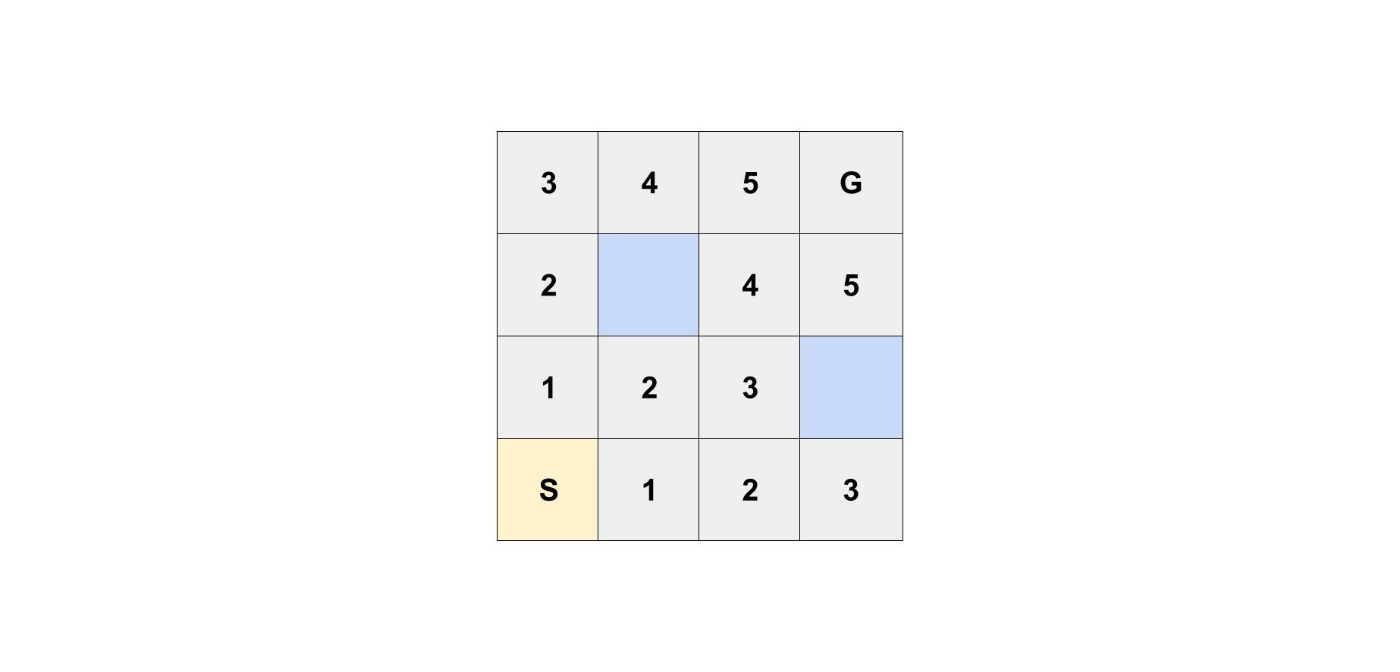
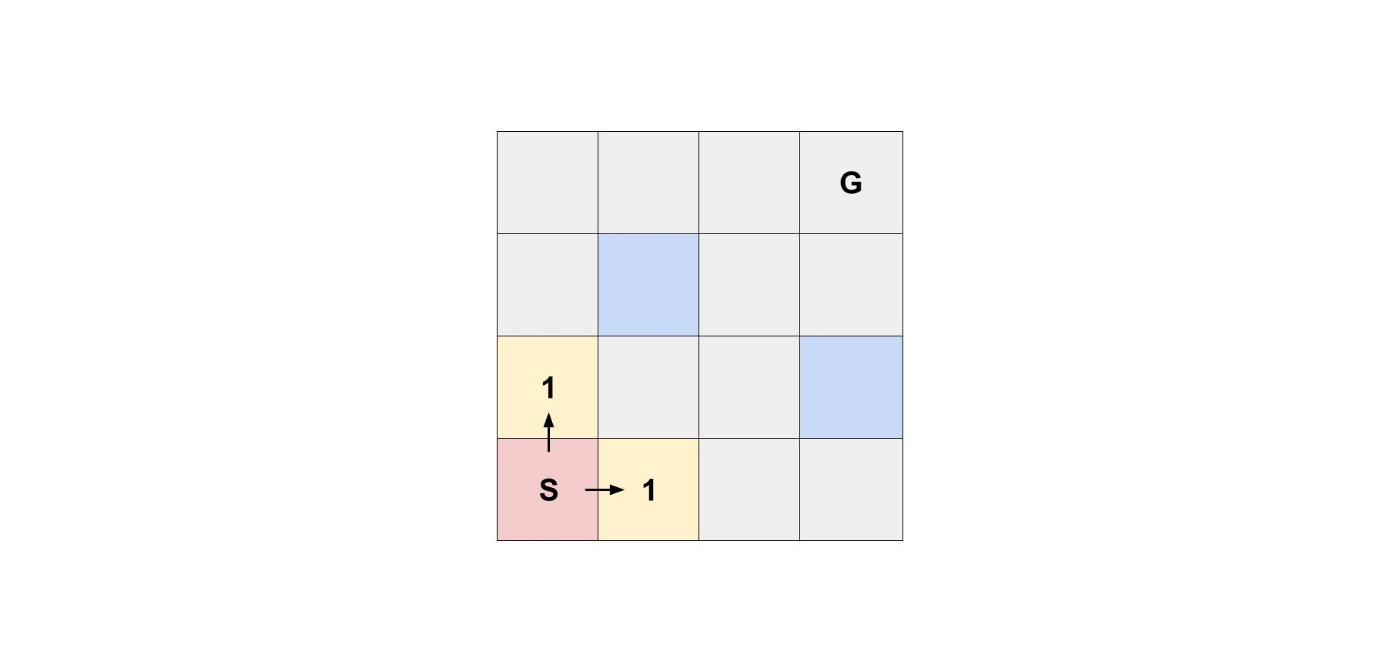
スタートから進むことが出来るマスは、上のマスと右のマスです。

グラフは、さまざまなものが互いにどのようにつながっているかをモデル化する方法でした。
迷宮において、マス同士が互いにどのようにつながっているかを表したグラフだと考えられます。

スタートから進むことができた2つのマスから、進むことができるマスを考えていきます。
幅優先探索は、スタートに近いところから順に探索していくアルゴリズムです。
そこで、次に探索なければならないマスは、スタートの上のマスと右のマスです。
最初にスタートの右のマスから行けるマスを考えるとします。

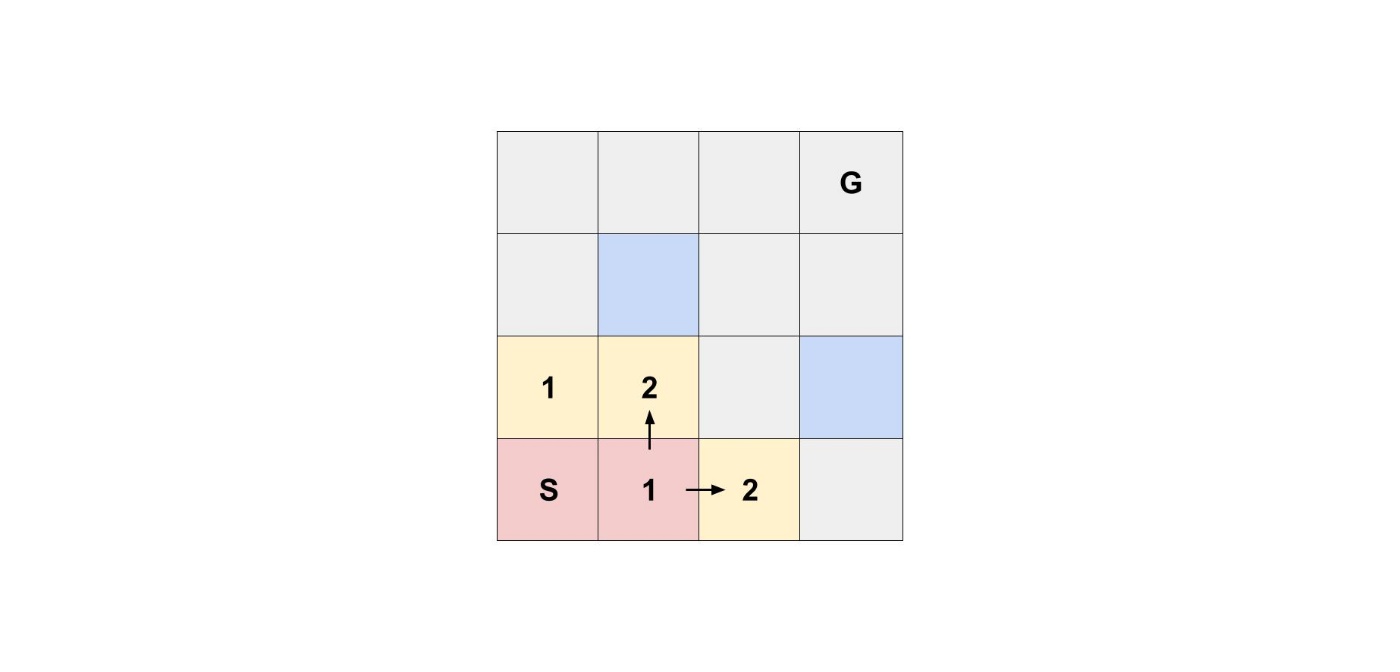
探索できるマスが増えましたが、スタートに近いところから順に探索していく必要があるため、
最初にスタートの上のマスから行けるマスを考える必要があります。

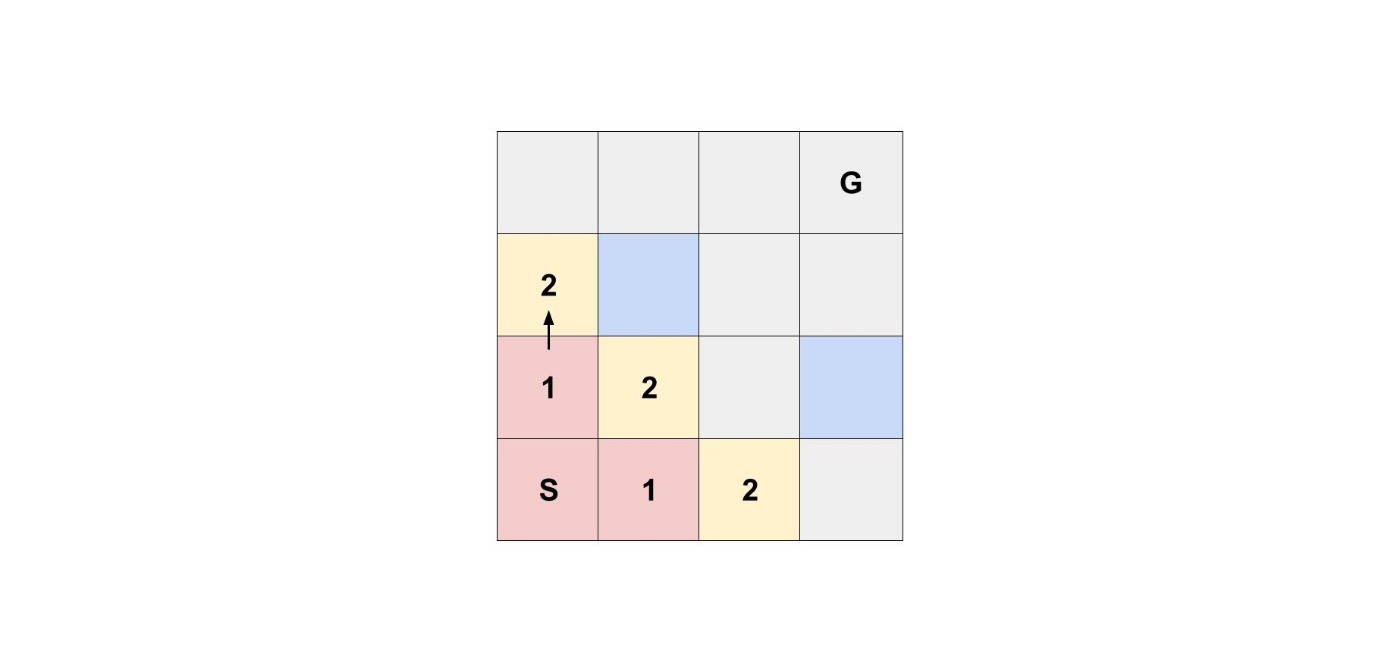
つまり、追加された順番にマスを探索する必要があるんです。
このアルゴリズムを実装するためには、先に入れたものが先に出るデータ構造が必要になります。
そのために、基本的なデータ構造の1つであるキューを使うことができます。

Queue (キュー)

少し前に紹介したデータ構造であるスタックは、後に入れたものが先に出る構造になっています。

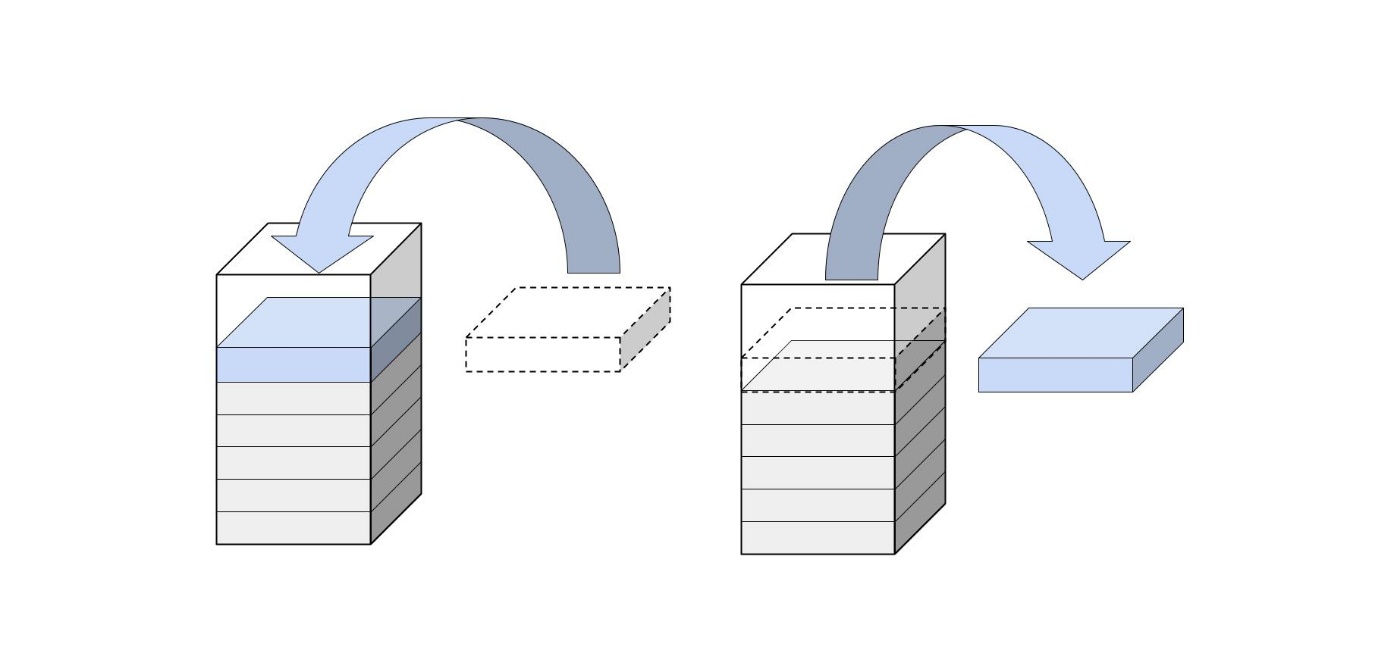
それに対して、キューは先に入れたものが先に出る構造になっています。
こちらの方が、生活の中でも「先着順」として使われているので身近なデータ構造だと思います。

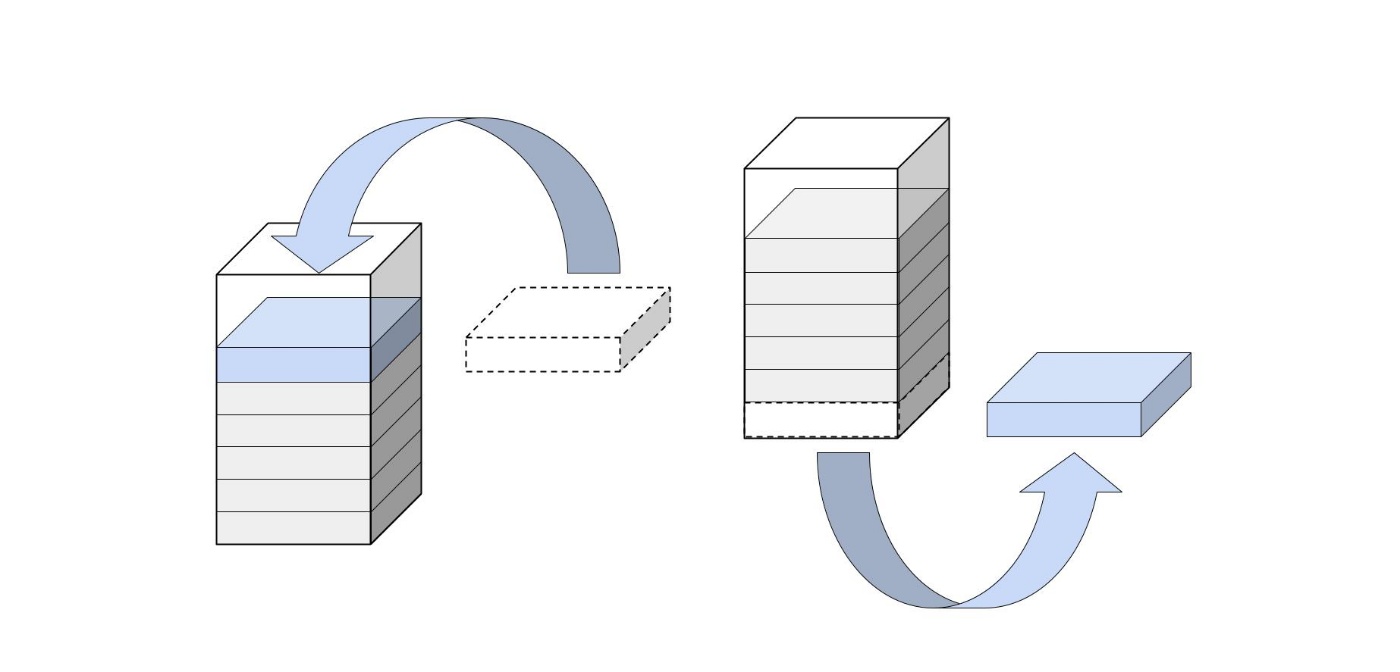
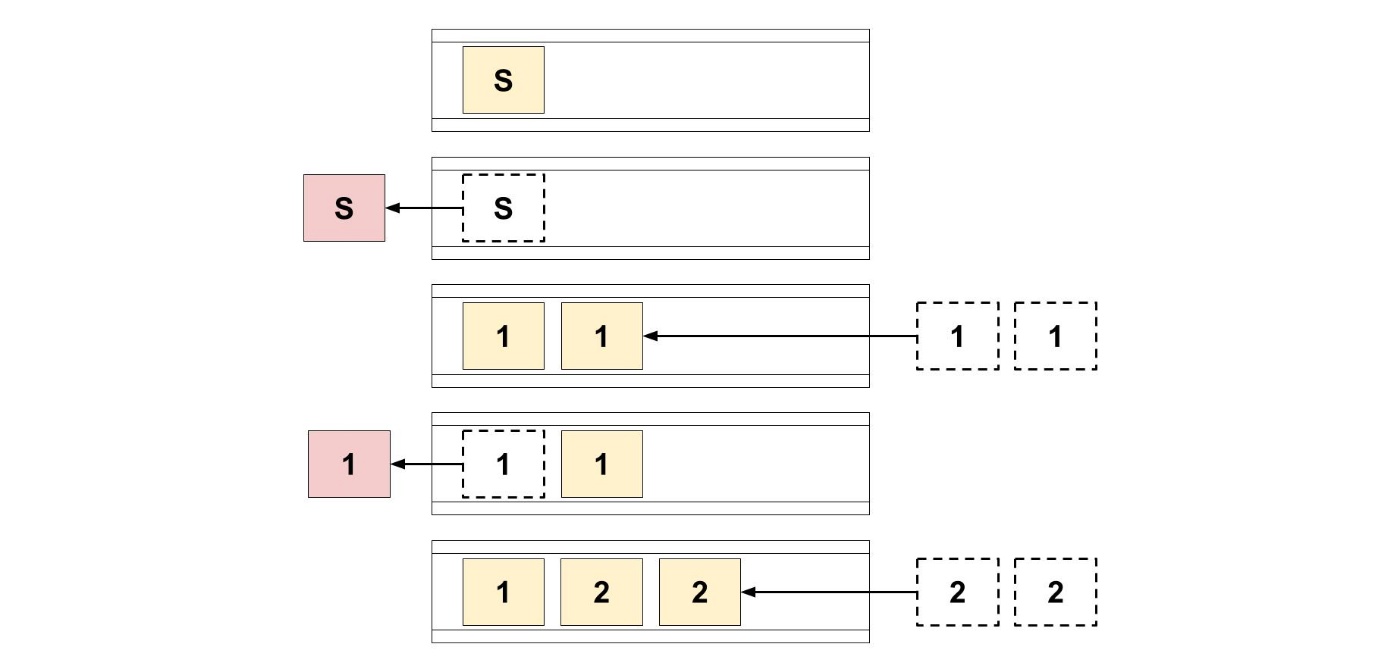
先ほどの迷宮の探索で、キューを使ってみましょう。

はじめに、スタートのマスをキューに追加しました。
もう追加できるものがないので、スタートのマスを取り出します。
スタートのマスから行ける2つのマスをキューに追加しました。
もう追加できるものがないので、追加したマスを取り出します。
このようにして行けば、スタートに近いところから順に探索していくことができそうです。

ここでは、幅優先探索の細かい実装までは紹介しません。
実装が知りたい方は、調べてみてください！

コーディングテストでこのような問題が出たときに、幅優先探索を実装していると間に合わないと思います。もし可能なのであれば、予め幅優先探索の実装ソースコードを作っておいた方が良いと思います。

幅優先探索の時間計算量を考えてみましょう。
幅優先探索は、エッジ伝って全てのノードを探索するアルゴリズムでした。
各ノードはキューに多くても一回だけ追加されて、取り出されます。
各エッジも多くても一回だけ探索されます。
それを合計して、幅優先探索の時間計算量は $O(V+E)$ となります。

V: vertices(頂点), E: edges(エッジ)

7. ダイクストラ法

幅優先探索は、最短距離を求めることができました。
ただし、重み付きグラフでは幅優先探索は使うことはできません。
重み付きグラフとは何であるかと、ダイクストラ法について学びます。

重み付きグラフ

迷宮の問題では、道は同じ長さだったのですが、現実でも道は同じ長さでしょうか？
現実では道によっては長さが違い、移動にかかる時間も異なります。

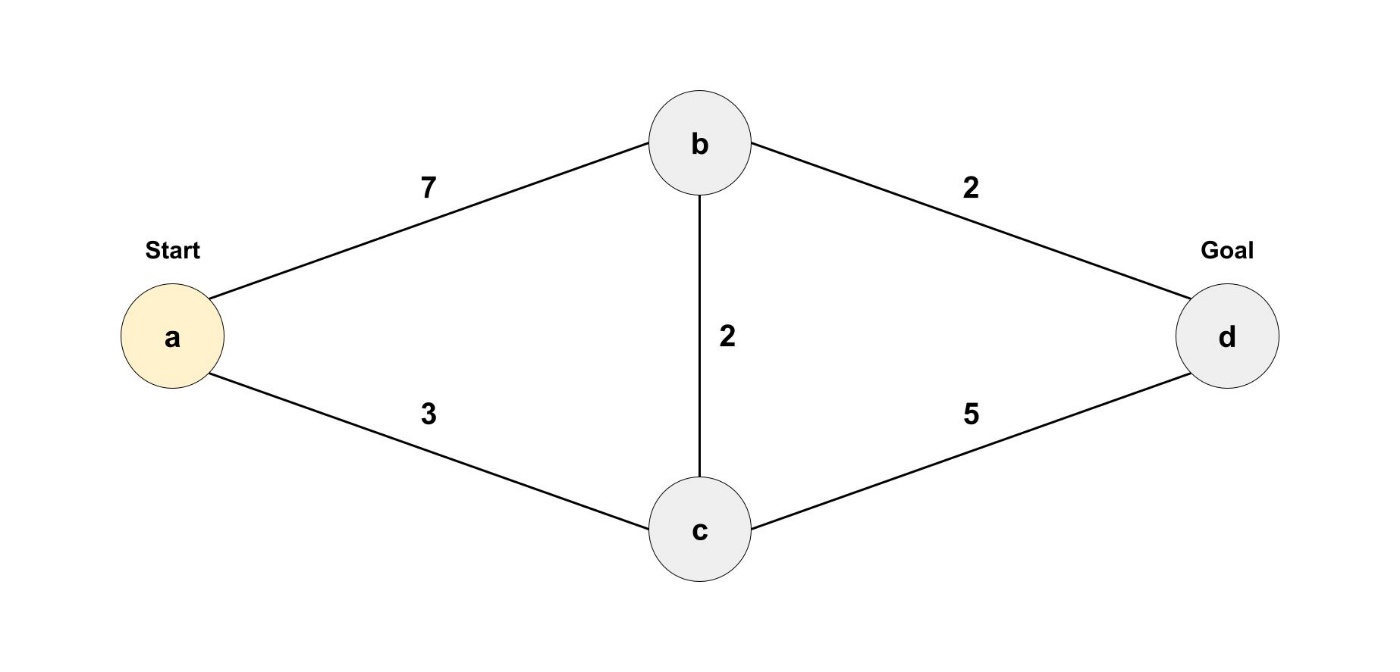
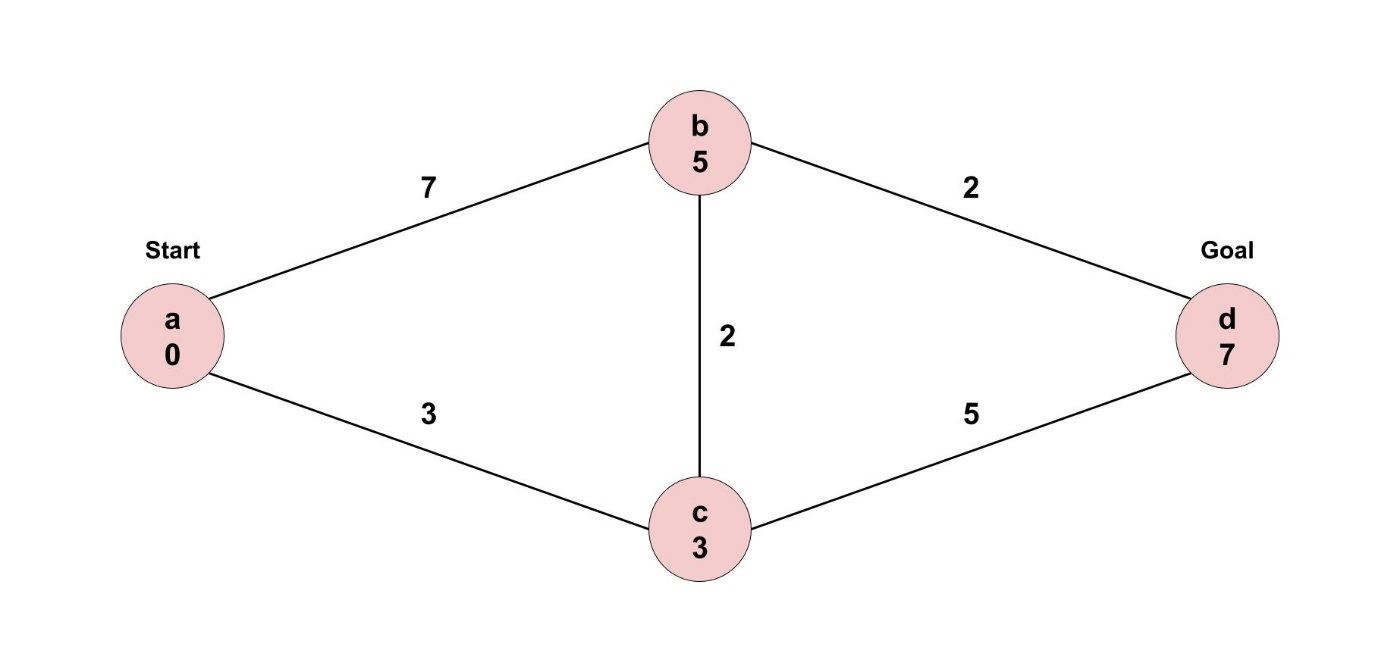
例えば、スタート地点のノードaから、ゴール地点のノードdを目指します。
幅優先探索では ノードa -> ノードb -> ノードd というルートが得られでしょう。

しかし今回はエッジに重みが付けられています。
ノードa -> ノードb -> ノードd というルートでは、9分かかるという感じです。

ここで、ノードa -> ノードc -> ノードd というルートを見てみましょう。
こちらのルートでは、8分しかかかりません。

さらに、ノードa -> ノードc -> ノードb -> ノードd というルートを見てみましょう。
一見遠回りに見えますが、7分しかかかりません。

こうした重み付きグラフの経路問題を解くアルゴリズムとしてダイクストラ法があります。

Dijkstra’s algorithm (ダイクストラ法)

今いるノードから行けるノードを探して、最短距離を記録しておく
その中で、一番近いノードに移動して、そのノードから行けるノードを探して、最短距離を記録しておく

ダイクストラ法では、スタート地点から各ノードまでの最短距離を記録していきます。
スタート地点からはじめていきましょう。
スタート地点までの最短距離は存在しないので、0分とします。

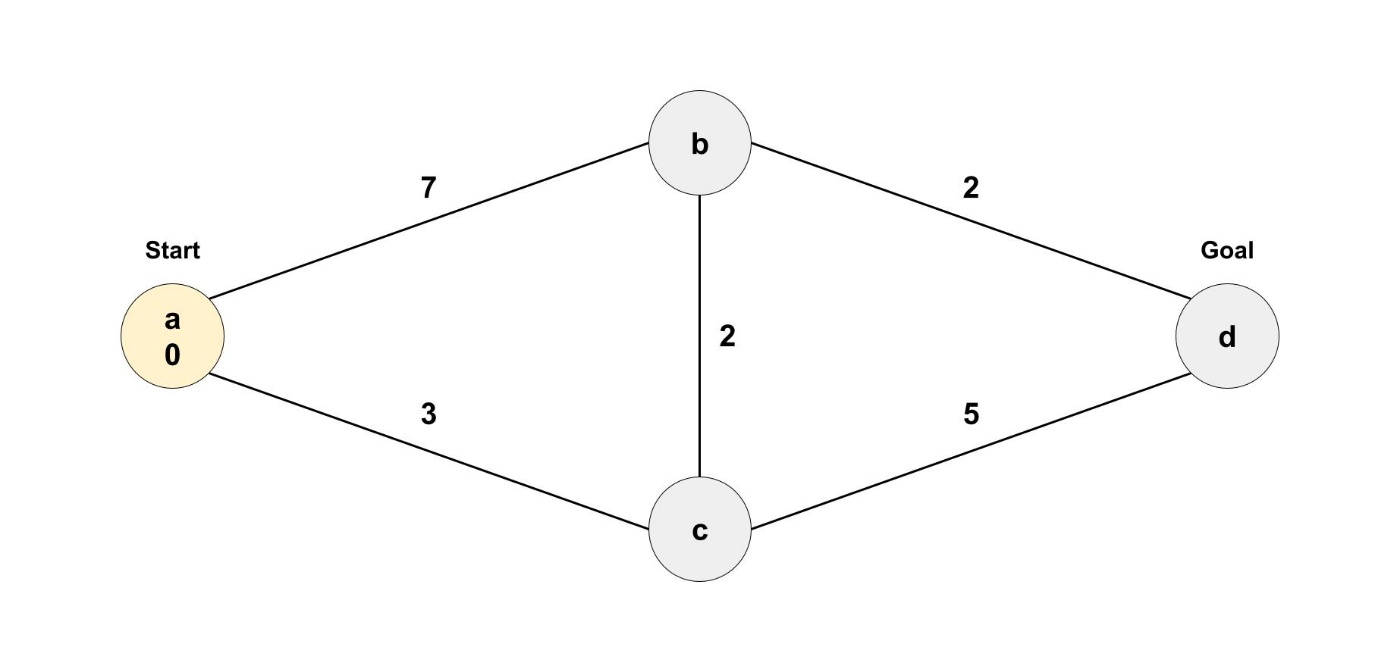
次に、今いる地点から行けるすべてのノードへの距離を更新します。
ノードaから行くことができるのは、ノードbとノードcです。
このときに、近いノードから辿っていくのがポイントです。

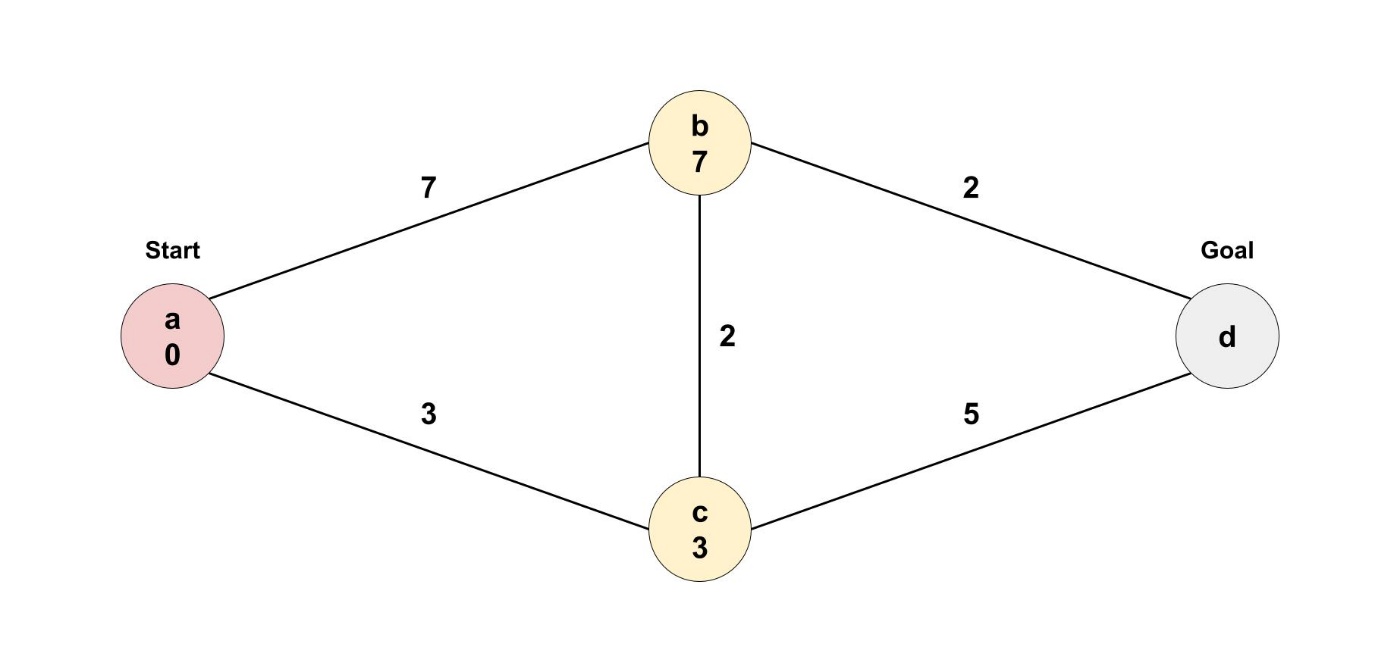
ここで、ノードcの方が近いので、ノードcから辿ることにします。
次に、今いる地点から行けるすべてのノードへの距離を更新します。
ノードcから行くことができるのは、ノードbとノードdです。
ここで、ノードbの最短距離が更新されましたね。

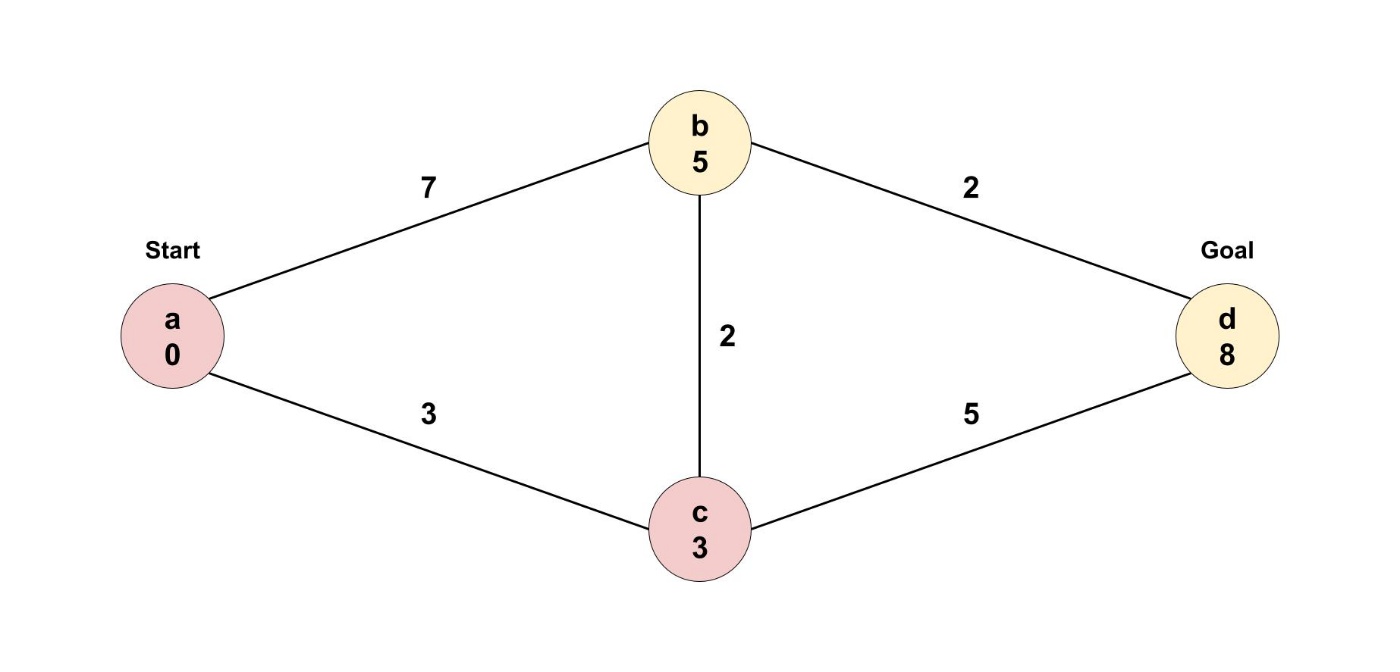
次に、訪れないといけないのは、ノードbでした。
今いる地点から行けるすべてのノードへの距離を更新します。
ノードbから行くことができるのは、ノードdです。
ここで、ノードdの最短距離が更新されましたね。

ノードbからノードcに訪れる必要はありません。
ノードcの方がノードaから近いので、ノードbから頑張っても最短距離を更新できないためです。
残念ながら、エッジの重みが負であるものがあると、このアルゴリズムが機能しなくなります。
ダイクストラ法は、すべての重みが正である場合に有効です。
負の重みがある場合は、ベルマンフォード法を使用する必要があります。

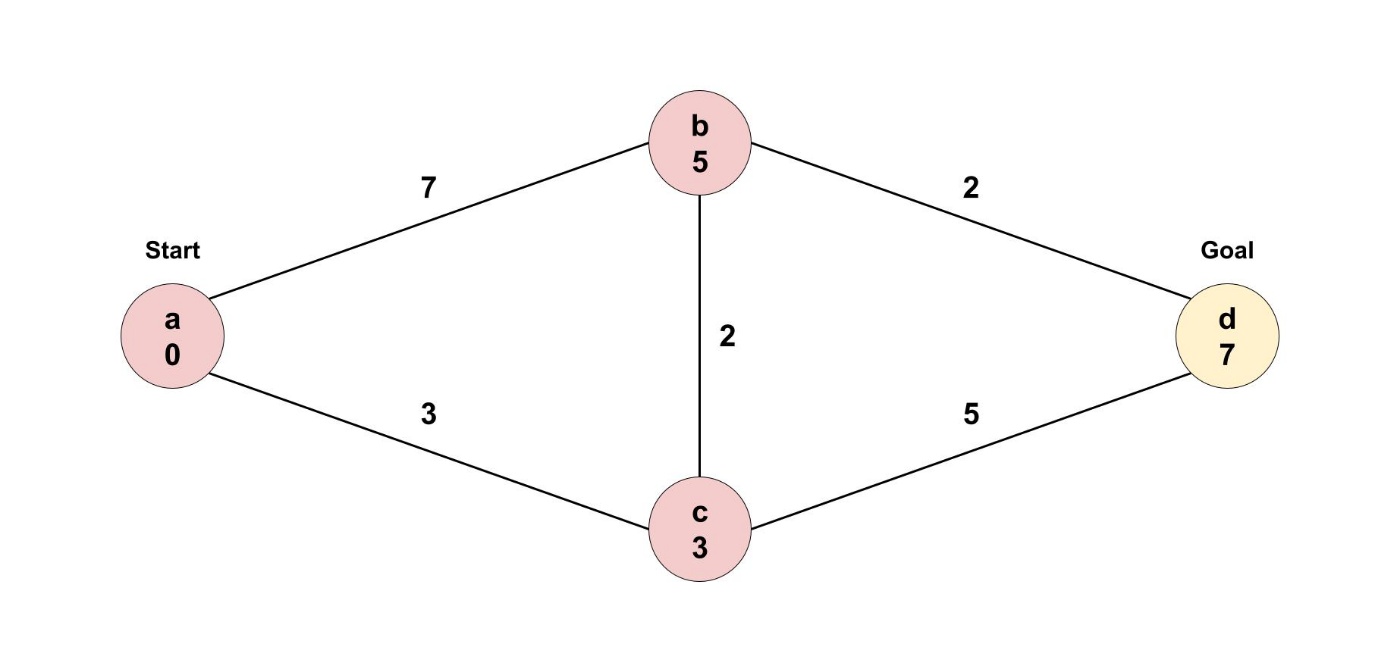
これで、最短距離が確定していないノードがなくなったので、終了しました。

ここでは、ダイクストラ法の細かい実装までは紹介しません。
気になる方は調べてみてください！

コーディングテストでこのような問題が出たときに、ダイクストラ法やベルマンフォード法を実装していると間に合わないと思います。もし可能なのであれば、予め幅優先探索の実装ソースコードを作っておいた方が良いと思います。

また、単純に実装するだけでは、時間計算量が $O(V^2)$ となってしまいます。
まだ紹介していないですが、ヒープなどを使えば $O((e+n) logn)$ まで抑えることができます。

8. 貪欲法

アルゴリズムによる高速な解が存在しない問題（NP完全問題）への取り組み方を学びます。
このような問題が出てきたとき、高速なアルゴリズムを見つけることができないので、
アルゴリズムによる高速な解が存在しない問題であることを見抜けることが重要になります。

そこで、高速な解が存在しない問題の中でも有名な問題を学んでいきましょう。
また、NP完全問題の近似解を高速に求めるための貪欲法についても学びます。

スケジューリング問題

あなたは大学生で、取れる必修科目の単位は早めに取りたいと考えています。
ここに、取ることができる授業のリストがあります。
時間が重なっている授業もあるので、すべての授業を取ることはできません。

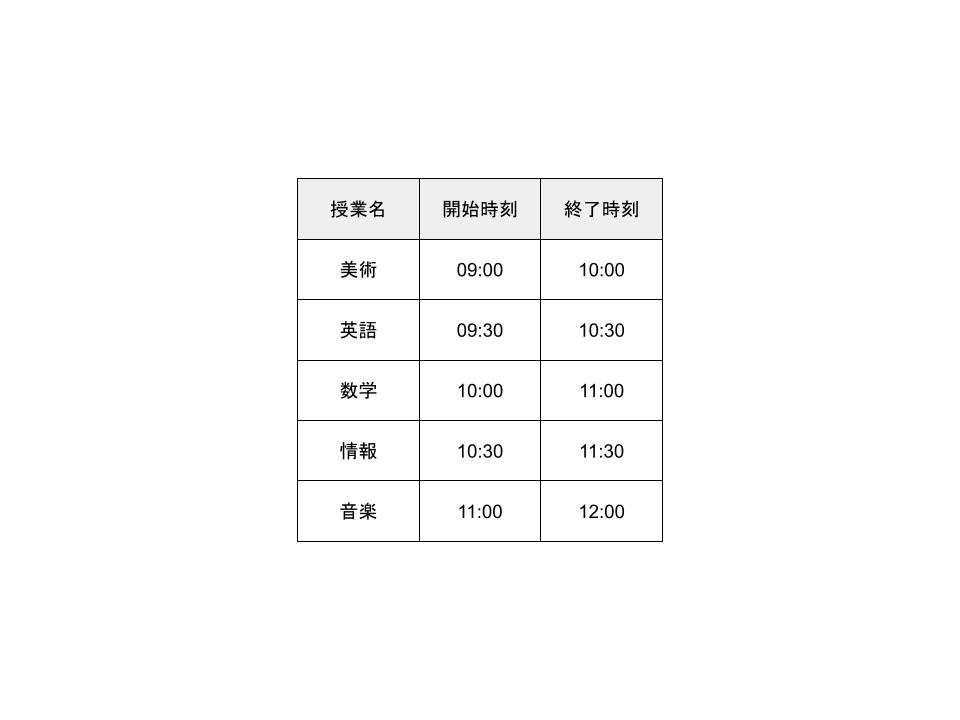
できるだけ多くの授業を取るために、どのような授業を選択すればよいでしょうか。
ここで、貪欲法を使ってみましょう。

最も早く終了する授業を選択します。
次に、最初の授業の後に始まるクラスを選びます。
これを繰り返します。

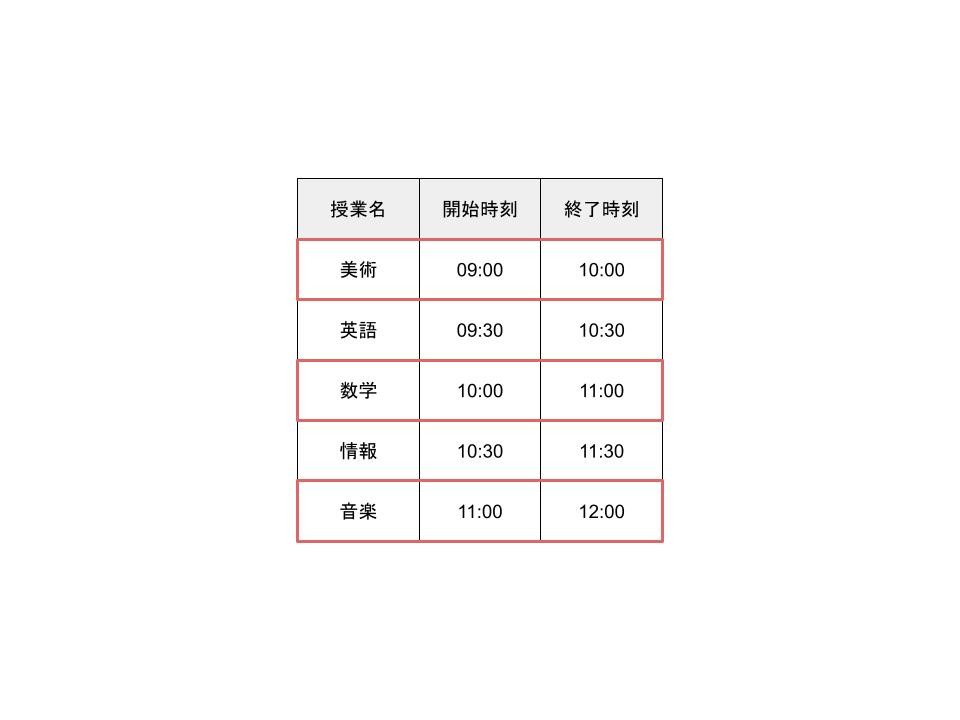
というわけで、取るのはこの3つの授業です。

貪欲法は、各ステップで最適な手を選ぶというシンプルなものです。
シンプルなのが、貪欲法の良いところです。

ナップサック問題

あなたは、お金持ちの社長の家に遊びに行きました。
そのときに、社長が使っていないものがあるから、持って帰っていいよと言ってくれました。

ナップサックを持ってきたので、そこに入るものなら持って帰れそうです。
ナップサックは、16キロまでしか入らないので全部は持って帰れません。

なるべく価値の高いものを持って帰るためには、何を持って帰ればいいでしょうか？
ここで、貪欲法を使ってみましょう。

ナップサックに入る一番高いものを選ぶ。
次に高いもので、ナップサックに入るものを選ぶ。
これを繰り返します。

オーディオ機器が一番高いので、これを持って帰りたいと思います。
30万円相当のものを持って帰ることができましたが、これが一番良かったのでしょうか？

もし、ノートパソコンとエレキギターを代わりに選んでいたら、
35万円相当のものを持って帰ることができたはずです。

この例では、貪欲法を使っても最適解を得ることができませんでした。
しかし、シンプルな方法で最適解にかなり近い解を得ることができました。

集合被覆問題

あなたは、自分の企業を宣伝するためにラジオCMを打ちたいと考えています。
放送局によってカバーしている地域が違うので、どの放送局でCMを出すか考える必要があります。
せっかくなら、全国のリスナーにCMを聴いてもらいたいですよね。
ここに放送局のリストがあります。

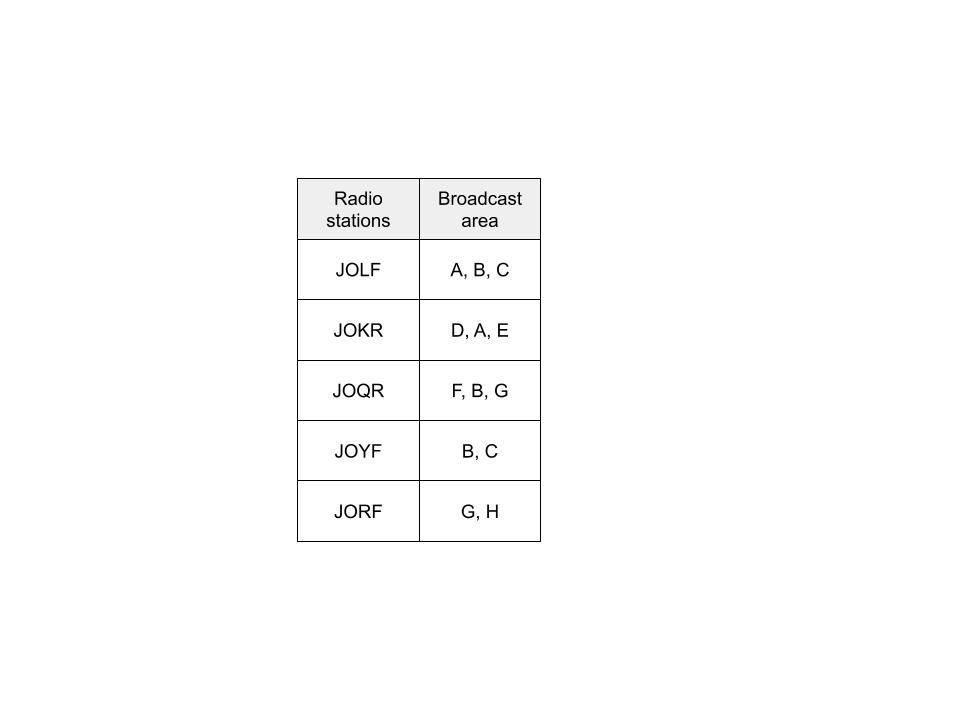
放送局によってカバーしている地域が違いますが、お互いに重複もあります。
47都道府県をカバーするために、どのように放送局を選べば最小限の数で済むでしょうか？

簡単そうに感じるかもしれませんが、これはよく知られた非常に難しい問題の一つです。
実際に解くためには、どうしたらいいのでしょうか？

すべての放送局の組み合わせを用意する。(組み合わせは $2^n$ 個あります。)
この中から、最小の放送局数で47都道府県をカバーする組み合わせを選びます。

放送局の組み合わせが $2^n$ 個あるというのは、どのくらい多いのでしょうか？
$n = 100$ のとき
$2^n ≒ 1.26 × 10^{30}$ となります。

放送局の数が５局くらいであれば良いのですが、
放送局が多ければ、計算することが難しくなってしまいます。

ここで、貪欲法を使うと以下のようになります。

まだカバーされていない地域を最も多くカバーしている放送局を選ぶ。
全州がカバーされるまで繰り返す。

貪欲法は近似アルゴリズムと呼ばれています。
最適解を計算すると時間がかかりすぎる場合、近似アルゴリズムが有効です。
近似アルゴリズムで重視されるのは、実行時間と最適解にどれだけ近似できるかです。

巡回セールスマン問題

あなたは、セールスマンで営業に行かなければならない都市があります。
ある都市から出発し、すべての営業先の都市に訪問して、また出発地点に戻ってきます。
ここで、どのような順番で都市を回るのが最短経路になるのでしょうか？

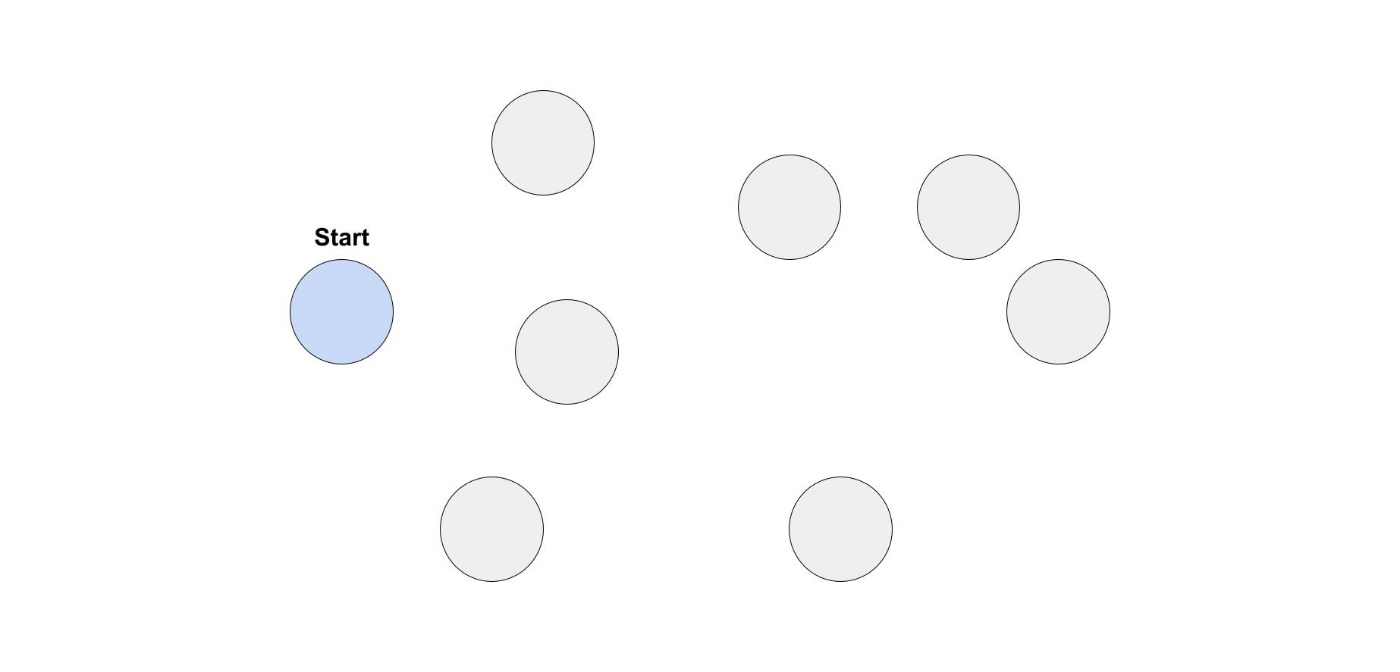
簡単そうに感じるかもしれませんが、解くのが難しいことで有名な問題です。
実際に解くためには、どうしたらいいのでしょうか？

すべての移動ルートの選び方を用意する。
この中から、最短経路のものを選びます。

すべての移動ルートの選び方は $n!$ 個あります。
$n!$ 個あるというのは、どのくらい多いのでしょうか？

$n = 100$ のとき
$n! ≒ 9.33 × 10^{157}$ となります。

営業先の都市の数が５個くらいであれば良いのですが、
営業先の都市が多ければ、計算することが難しくなってしまいます。

ここでは、局所探索法という近似アルゴリズムを用います。
局所探索法は貪欲法と並ぶ、代表的な近似アルゴリズムの一つです。

局所探索法では、現在の解のごく一部だけ修正していく方法です。
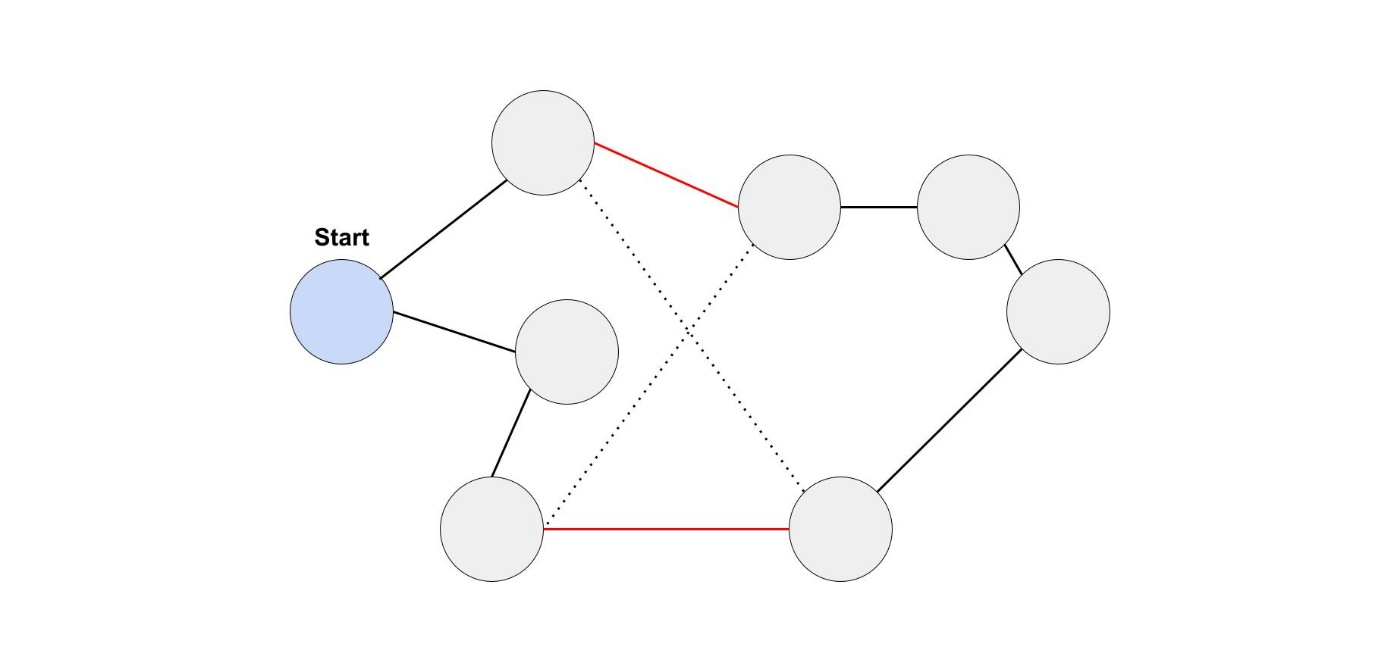
巡回セールスマン問題では 2-opt が良く使われます。

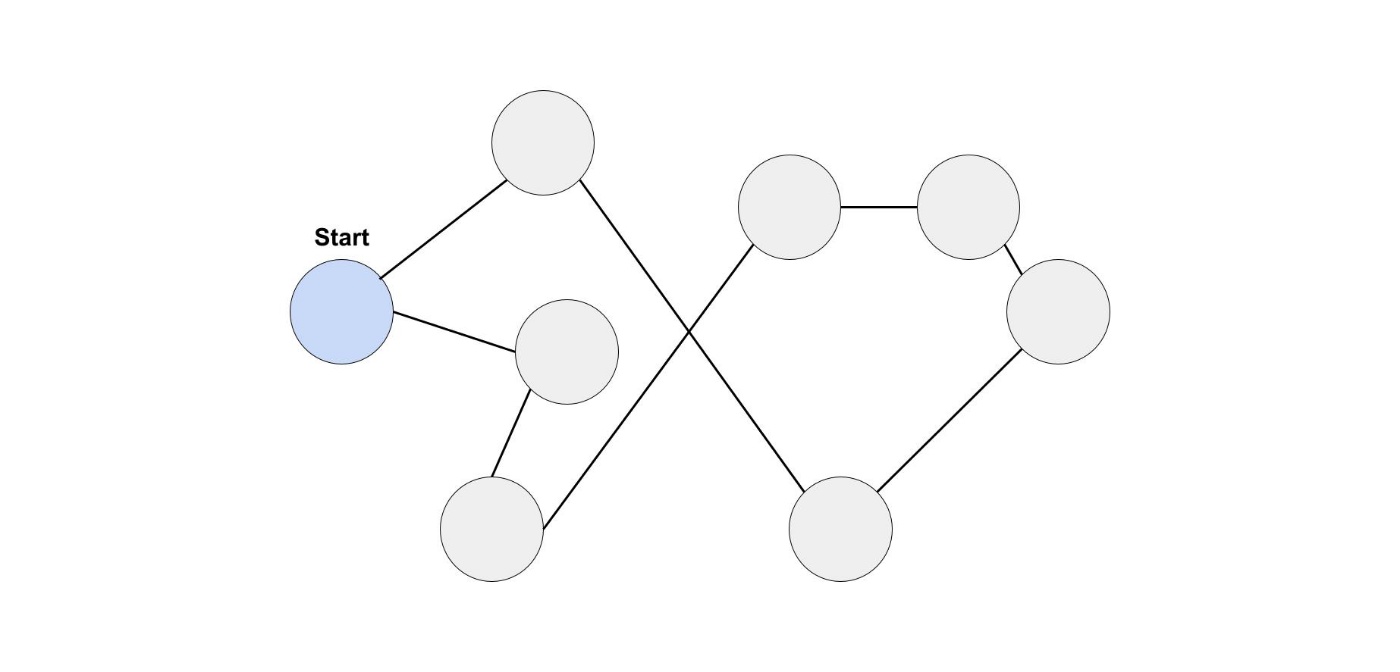
2-opt はある移動ルートから2つの辺を削除して、
2つの辺を繋ぎ直すことを改善ができなくなるまで繰り返すアルゴリズムです。

NP完全問題を見抜く方法

紹介した問題以外にも、アルゴリズムによる高速な解が存在しない問題はたくさんあります。
このような問題に出会ったときには、以下の手順を取る必要があります。

NP完全問題だと分かる
完璧に解こうとするのをやめて、代わりに近似アルゴリズムを使って解く

しかし、今取り組んでいる問題がNP完全であるかどうかを判断するのは難しいです。
なぜなら。簡単に解ける問題とNP完全問題の違いがほとんどないためです。

例えば、幅優先探索やダイクストラ法など最短経路の話をしました。
A地点からB地点に行く最短経路を計算する方法はあるのですが、
巡回セールスマン問題を計算する方法はありません。

今回紹介した問題と似たような問題が出て来たときには、特に注意しましょう。

9. 動的計画法

動的計画法とは、難しい問題を小問題に分割し、その小問題を先に解くことによって解決する手法です。
似たようなアプローチに分割統治法があります。

難しい問題を小問題に分割するという点は同じですが、分割統治法とは少し異なります。
分割統治法は小問題から得られた解をまとめていくことで、全体の解を得る方法でしたが、
動的計画法では、とりあえず小問題を解いておき、必要なときに解を取り出して使うという方法です。

ナップサック問題

ナップサック問題をもう一度見てみましょう。
今度は、4キロまでのものを入れることができるナップサックを持っています。
なるべく価値の高いものを持って帰るためには、何を持って帰ればいいでしょうか？

簡単な解法としては、すべての組み合わせを考えることでした。
例では、3つの品物しかないので、8つの組み合わせがあります。
4つなら16つの組み合わせ、品物が1つ追加されると組み合わせの数は2倍になります。
組み合わせの数が $2^n$ あるので、実行時間は $O(2^n)$ となります。

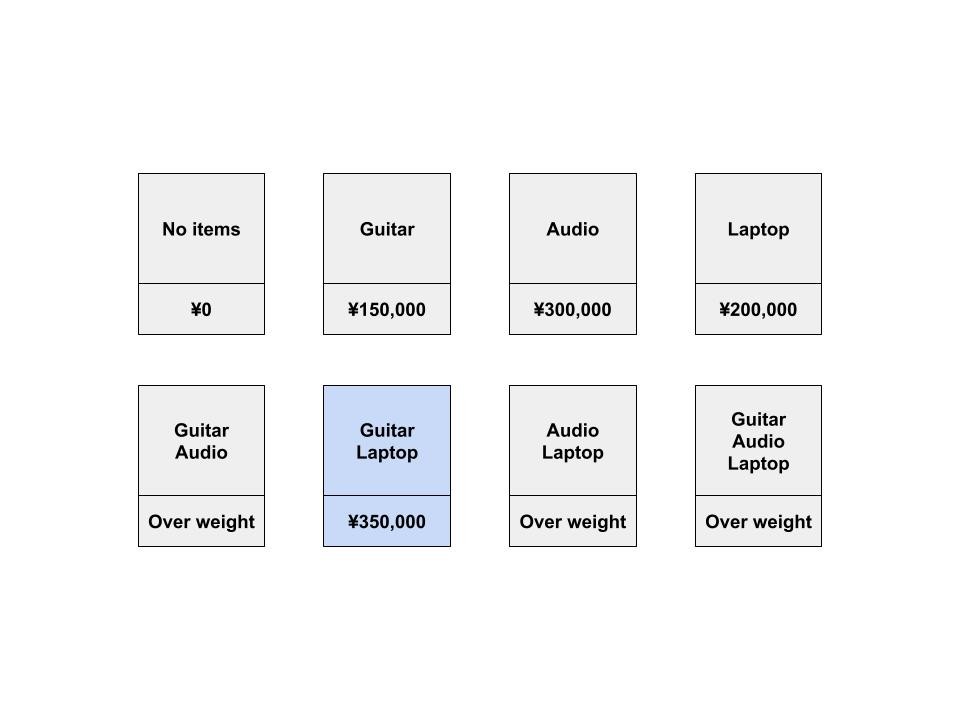
貪欲法をを使えば、近似解を得られることは知っています。
ですが、動的計画法を使えば、最適解を計算することができます。

動的計画法を使って、ナップサック問題を解いていきましょう。
動的計画法を使うときは、表を用意します。
表の行は品目で、列はナップサックの重さです。

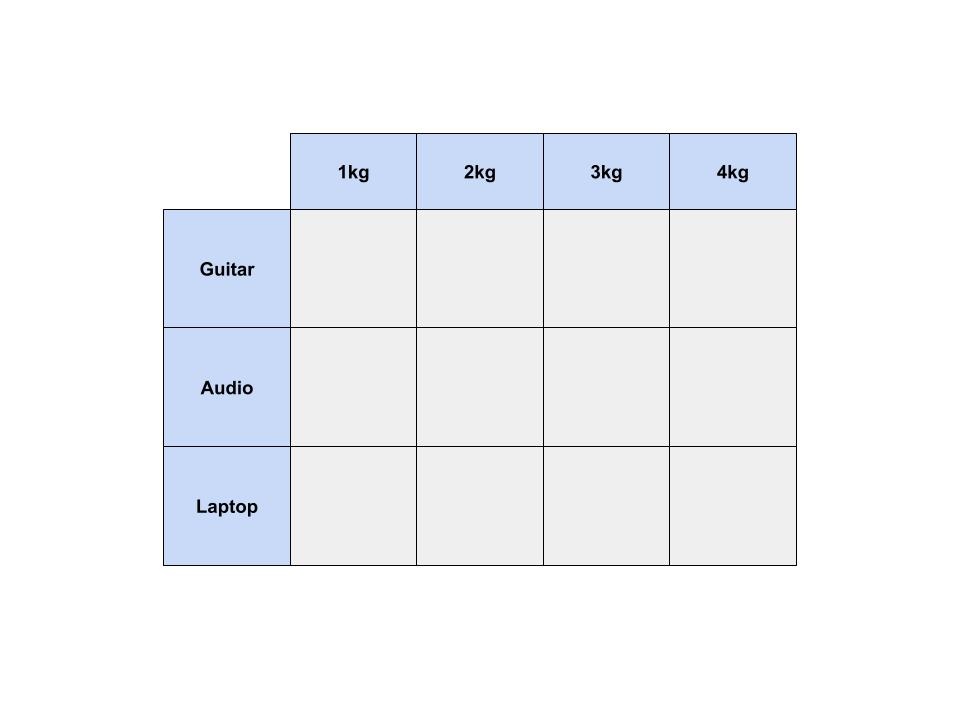
1kgまでしか入らないナップサックから4kgまで入るナップサックがあると思ってください。
最初は表がすべて空の状態ですが、徐々に表を埋めていくことで、答えを得ることができます。

まずは、エレキギターの列から考えます。
1kgまでしか入らないナップサックがあるとします。
ここでは、エレキギターしか選ぶことができません。
このナップサックの価値を最大にするには、どうしたらいいでしょうか？

エレキギターも1kgなので、ナップサックに入れることでできます。
これよって、このセルの価値は ¥0 から ¥150,000 となりました。

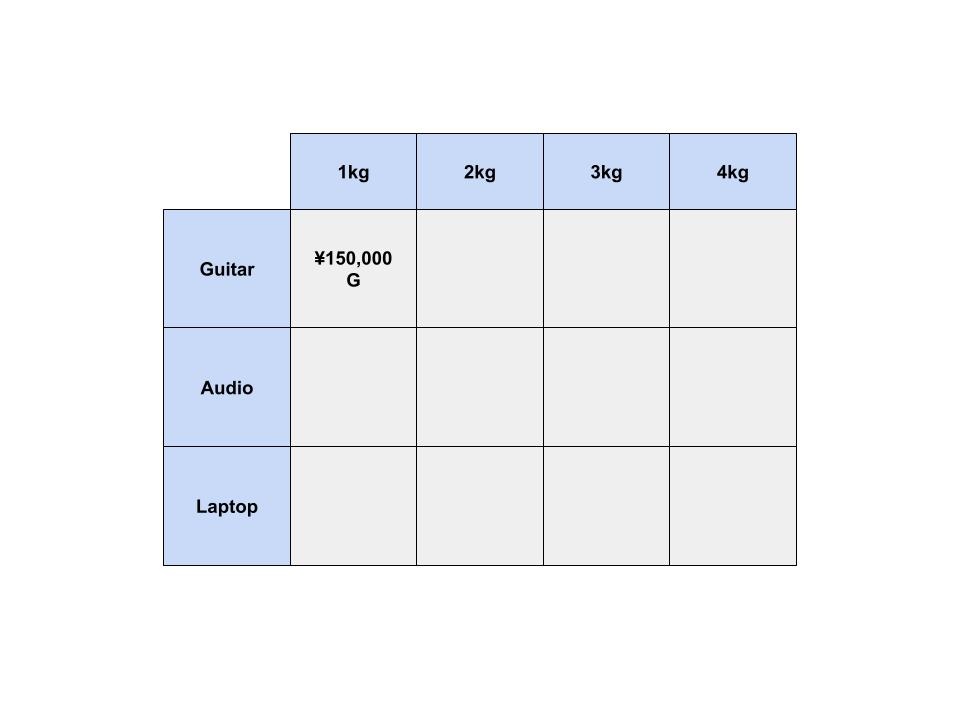
残りのセルも同様に埋めていきたいと思います。

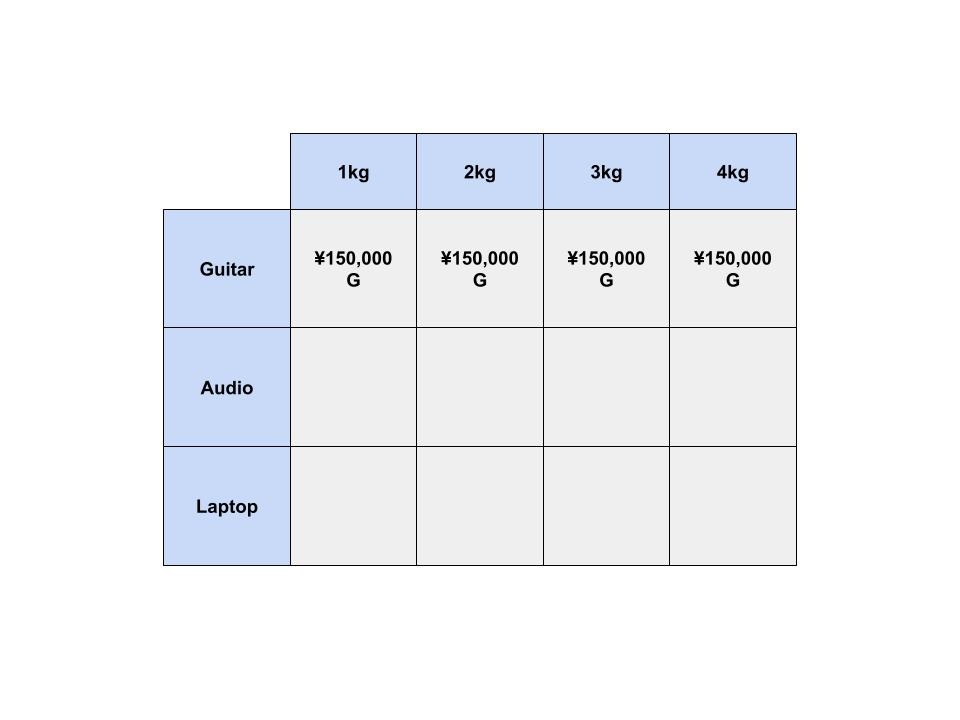
次に、オーディオ機器の列を考えます。
1kgまでしか入らないナップサックがあるとします。
ここでは、オーディオ機器かエレキギターを選ぶことができるようになりました。
どの列でも、その列の品物か、その上の列の品物を選ぶことができます。
このナップサックの価値を最大にするには、どうしたらいいでしょうか？

オーディオ機器は4kgなので、ナップサックに入れることができません。
エレキギターを選ぶことが、このナップサックの価値を最大にする方法に変わりませんでした。

では、4kgまでしか入らないナップサックがあるとします。
エレキギターかオーディオ機器を選ぶことができます。
オーディオ機器を入れることで、このセルの価値は ¥150,000 から ¥300,000 となりました。

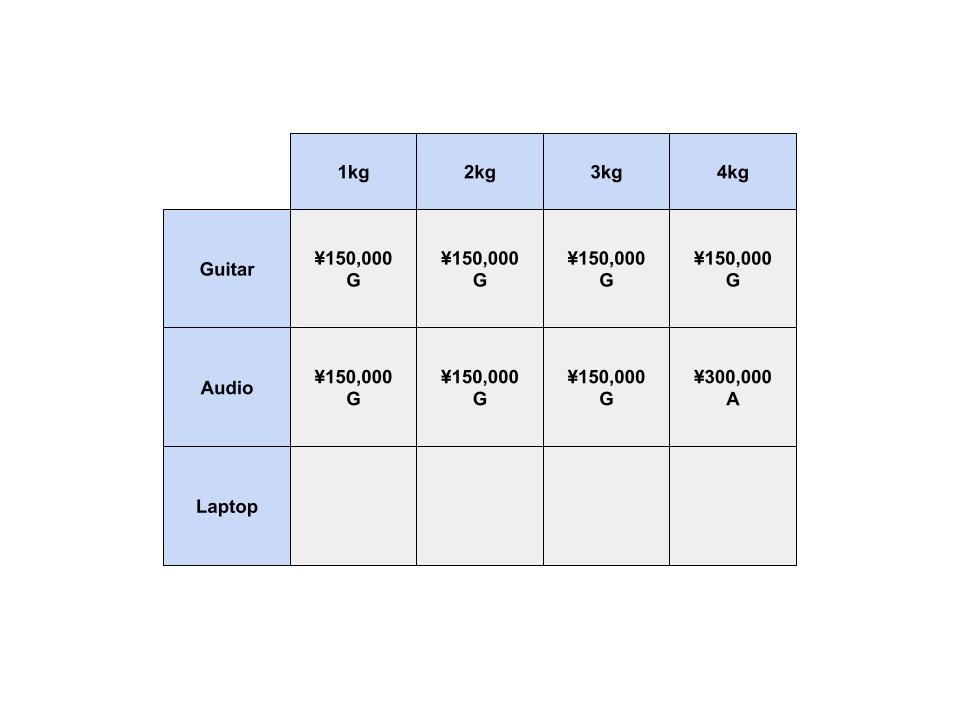
最後に、ノートパソコンの列を考えます。
ノートパソコンの重さは3kgなので、1kgや2kgまでしか入らないナップサックには入りません。
では、3kgまでしか入らないナップサックではどうでしょうか？
ここでは、エレキギターかノートパソコンを選ぶことができます。
ノートパソコンを入れることで、このセルの価値は ¥150,000 から ¥200,000 となりました。

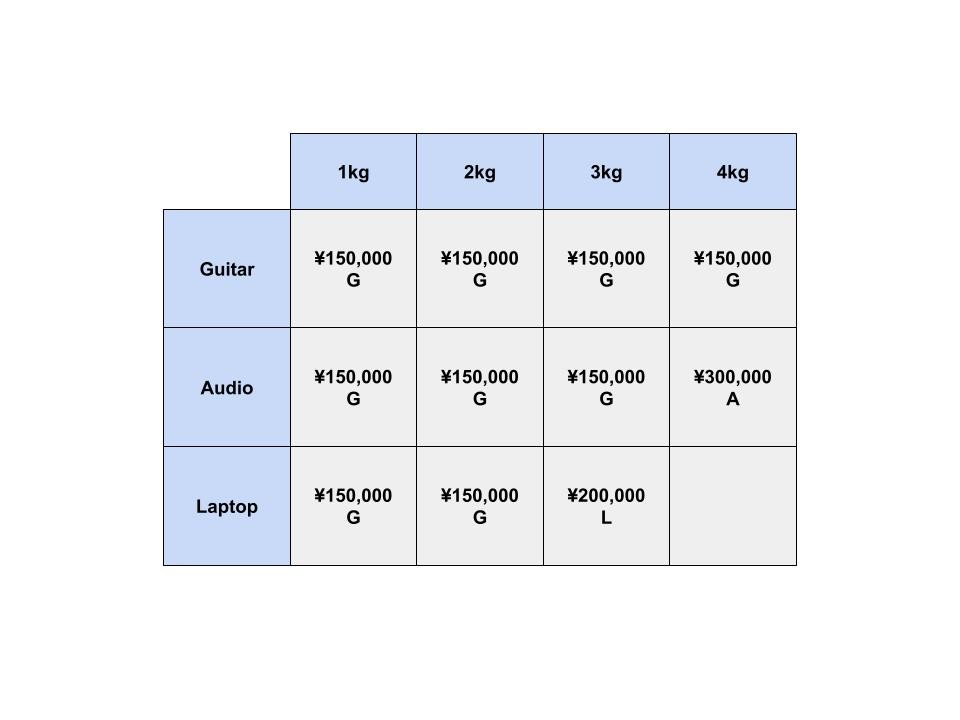
では、4kgまでしか入らないナップサックではどうでしょうか？
ここでは、オーディオ機器かノートパソコンかを選ぶことができます。
オーディオ機器を入れると、このセルの価値は ¥300,000 ですが、
ノートパソコンを入れると、このセルの価値は ¥200,000 となってしまします。

しかし、ノートパソコンは3kgしかないので、1kgの空きがあります。
ここで、わざわざ1kgのナップサックを計算してきた恩恵を受けることができそうです。
今までの計算によると、1kgのナップサックには、エレキギターを入れるのが最もよさそうです。
そこで、実際には「オーディオ機器」か「ノートパソコンとエレキギター」を選ぶことができます。
後者を入れることで、このセルの価値は ¥300,000 から ¥350,000 となりました。

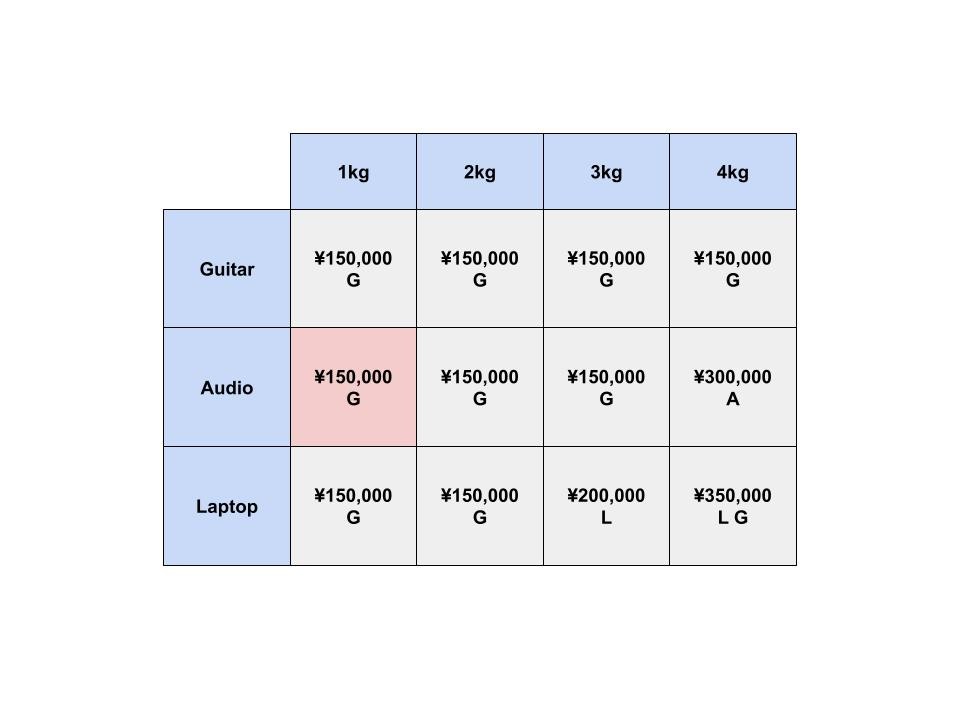
これを一般化すると、このようになります。

i 行 j 列のセルに選ぶ品物は、以下の2つのどちらか良い方になります。

今までで一番良かった品物 (i - 1 行 j 列にある品物)
現在の列の品物 + 残った重さに丁度良い品物 (i - 1 行 j - 品物の重さにある品物)

さっきの「ノートパソコンとエレキギター」を選ぶ過程で確認してみましょう。

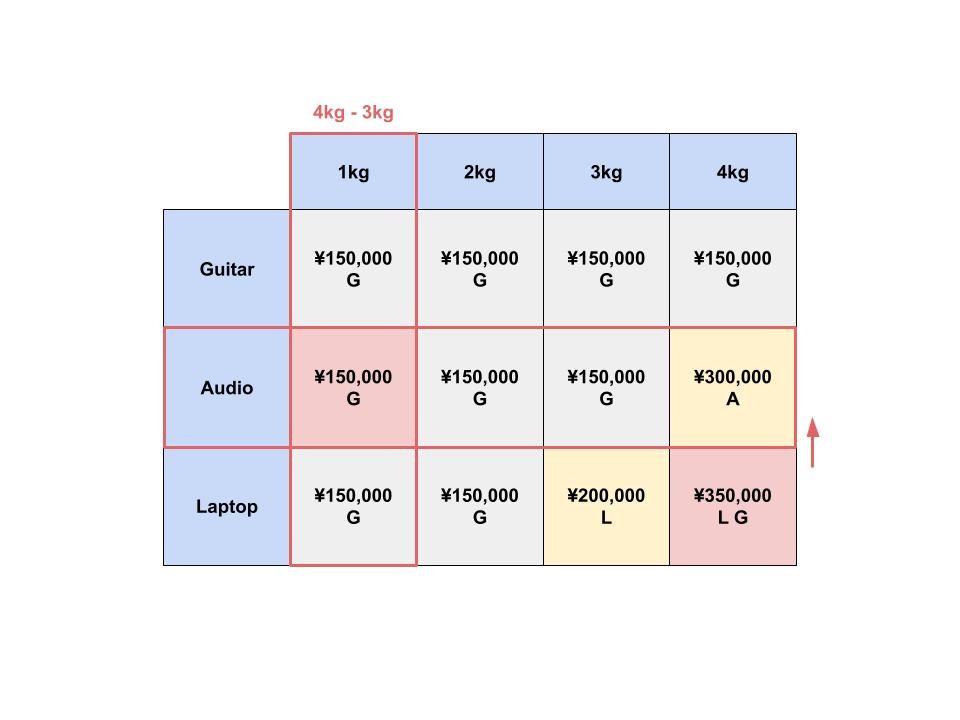
動的計画法でナップサック問題を解くときの時間計算量を考えてみましょう。
行が商品の個数分 = $n$ 個
列が0からlまで = $l+1$ 個
の表を埋めることで結果を求めることができました。

よって、時間計算量は $O(nl)$ となります。

今回動的計画法を使う例として紹介したのは、ナップサック問題でした。
他にも動的計画法を使うパターンはいくつかあるかもしれませんが、この例が一番有名だと思います。

問題を解くときに、ナップサック問題を知っていれば動的計画法を思いつけると思います。
逆にナップサック問題を知らないと動的計画法は思い浮かばないでしょう。
有名な例を知るだけでも、問題を解くときに新たな視点で解法を考えられるのではないでしょうか。

10. 二分探索木

あなたは、あるアプリのログイン機能を実装する必要があります。
ユーザーがログインするときに、そのユーザー名が存在するかどうかを調べないといけません。
しかし、ユーザーの数が膨大なため、巨大な配列を確認しないといけません。
このとき、あなたはどうしますか？
二分探索という探索アルゴリズムを知っているので、二分探索を使って実装することができます。

また、新しいユーザーが登録するたびに、ユーザー名を配列に追加します。
しかし、二分探索はソート済み配列に対して使えるので、追加した後にソートする必要があります。
毎回ユーザーが増えるたびに巨大な配列をソートするのは、効率が良くありません。

そこで、ユーザー名を配列の正しい位置に直接入れることができれば、良いと思いませんか？
二分探索木というデータ構造を使うことで、こういった問題を解消することができます。

Binary search tree (二分探索木)

二分探索木は次のようなものです。

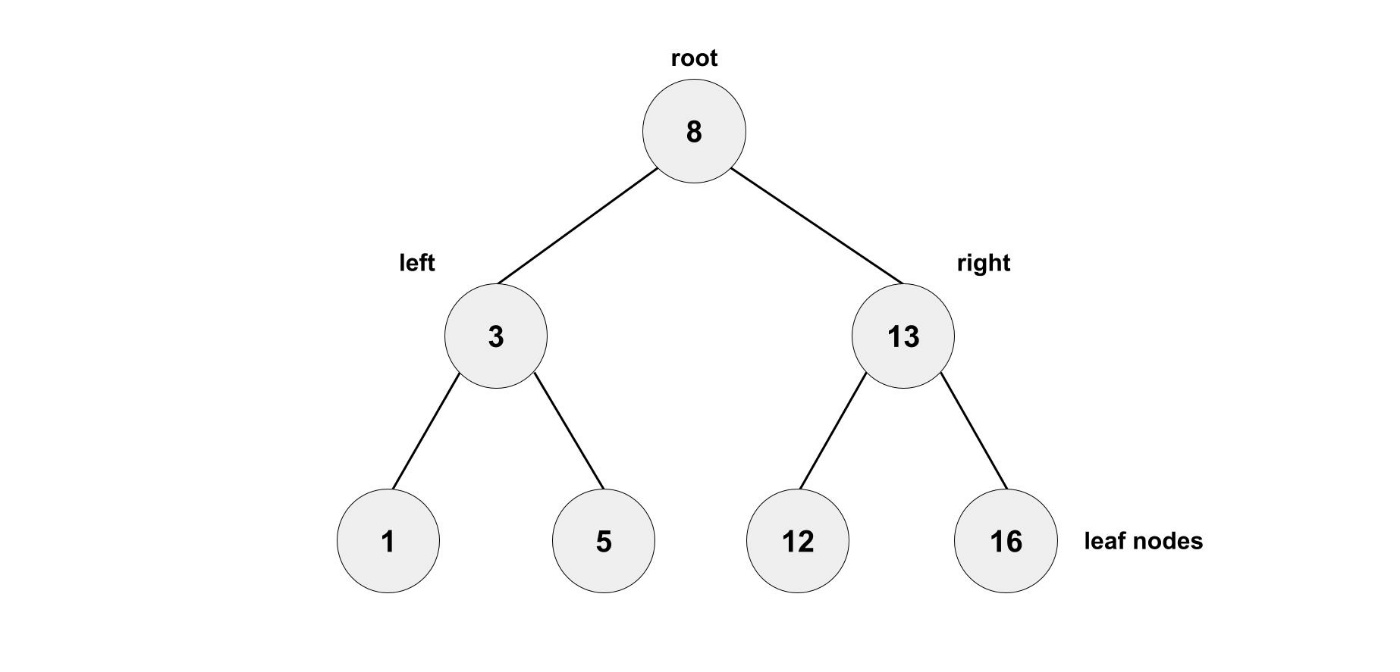
木構造は、ノードをエッジからなるグラフ構造の一つです。
二分木では、一つのノードからは多くても二本の枝が枝分かれしていきます。
自分の上のノードのことを親ノード、下のノードのことを子ノードと言ったりします。

親の左側のノードの値が必ず親よりも小さく、
右側のノードの値が必ず親よりも大きくなっている二分木のことを二分探索木と呼びます。

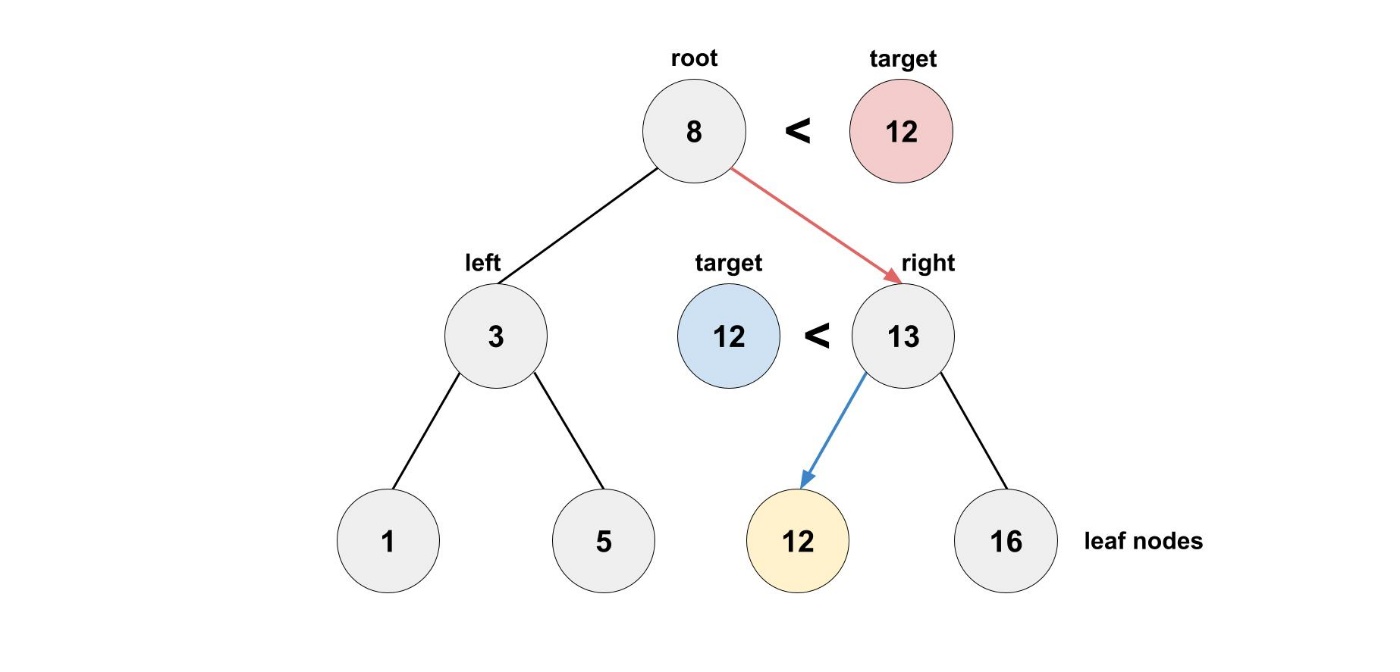
例えば、12を探したいと思います。
ルートノードの8を比較すると12は大きいので、右の子ノードに進みます。
次のノードの13を比較すると12は小さいので、左の子ノードに進みます。
そうすると、12を見つけることができました。
二分探索と同じように探索することができます。

まだ、二分探索よりも二分探索木を選ぶべきなのか判断できません。
そこで、実行時間を比較したいと思います。
二分探索の実行時間は最悪で $O(log n)$ でした。
二分探索木の実行時間は平均で $O(log n)$ で、最悪で $O(n)$ です。

ただし、二分探索を使うには配列がソートされている必要がありました。
しかし、二分探索木の方が、挿入や削除の平均時間は圧倒的に早いです。
挿入や削除の実行時間も平均で $O(log n)$ です。

ここで重要なのは、性能は木のバランスが取れているかどうかにかかっているという点です。
木が右に偏っているとすると、検索するときに二分探索の恩恵を受けるとこができません。
そこで、赤黒木のような木のバランスを調整するような実装もあります。

Heap (ヒープ)

二分木を使った基本的なデータ構造であるヒープについても説明したいと思います。
ヒープは優先度付きキューの1つです。

キューは先に入れたものが先に出る構造になっていました。

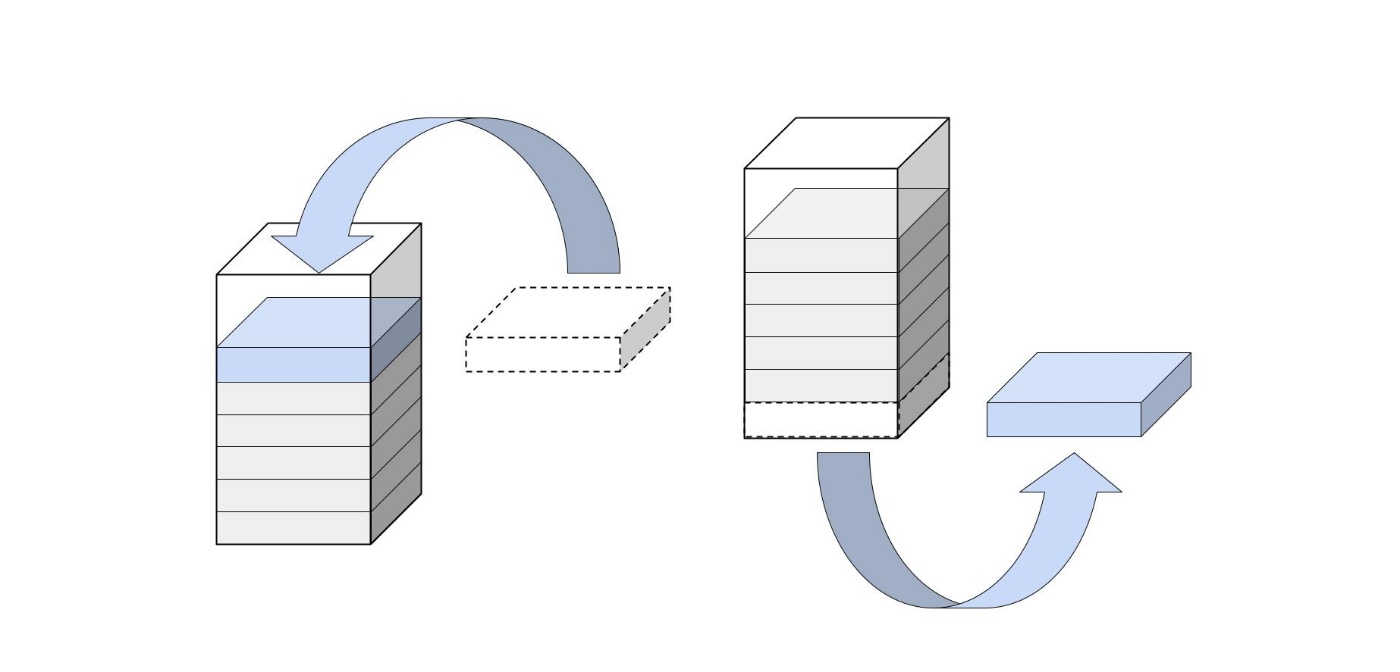
優先度付きキューは、含まれる要素が何らかの優先度順に取り出されるという特徴を持っています。
キューは、生活の中でも「先着順」として使われているので身近なデータ構造だと思います。
優先度付きキューは、それに比べると特殊なデータ構造ですが、考え方は簡単です。

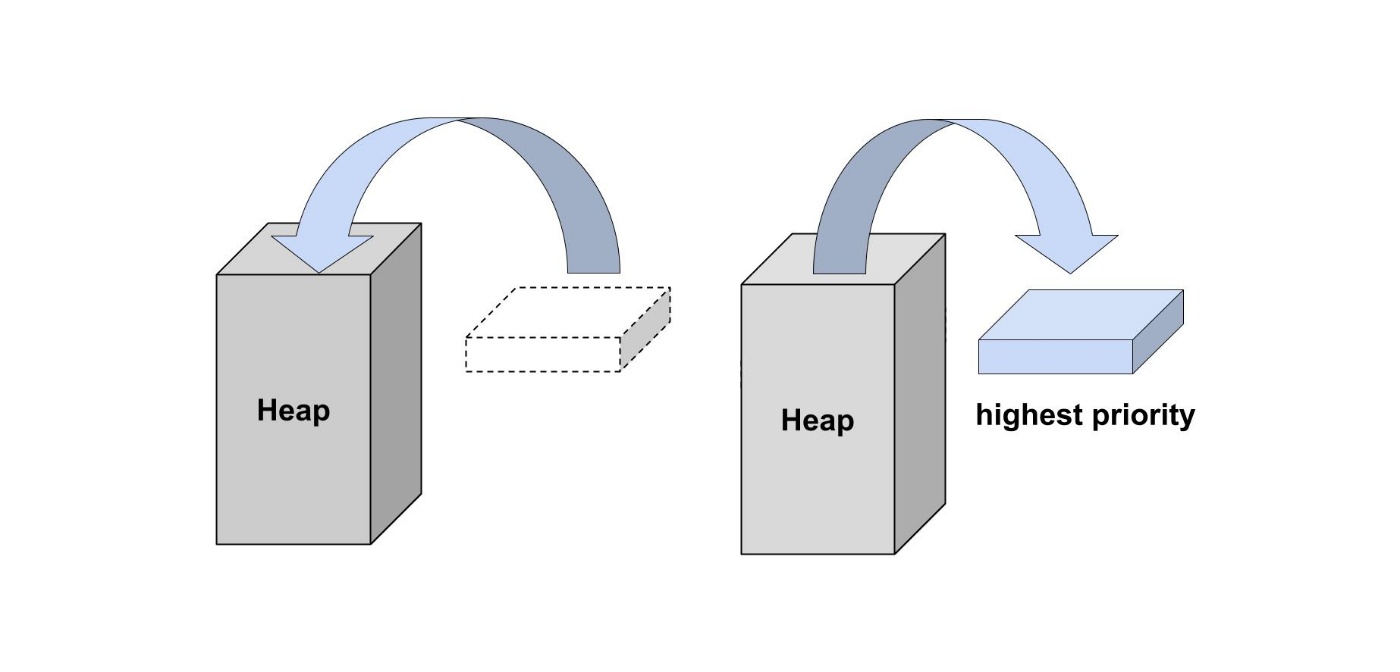
ヒープを使うと、必ず一番優先順位が高いものを取り出すことができます。
ここで、注意しなければならないのが、ヒープの中がソートされているわけではないという点です。

あなたは、スーパーで買い物をしていて、何枚か半額クーポンを持っているとします。
もちろん、出来るだけ高い値段の品物に対して割引を適用したいですよね。

一番簡単な方法としては、品物を値段順に並び替えて、最も値段の高いものから選ぶ方法です。
しかし、ここでクーポンの説明を読むと驚きの内容が書かれていました。
なんと、同じ品物に何枚でもクーポンを使うことができるのです。

そうするとやり方を見直す必要があります。
品物を値段順に並び替えて、最も値段の高いものから選びます。
その品物を半額にしてから、品物を値段順に並び替えて、また最も値段の高いものから選びます。

二分探索木のときもこんな問題がありましたね。
要素の追加や削除を行うと、再び並び替えをする手間がかかるという問題です。
一番値段を高いものを知りたいだけなのに、全体を並び替えをするのは効率がよくありません。
ヒープというデータ構造を使うことで、こういった問題を解消することができます。

ヒープは要素を追加したり削除しても、
効率よく最も優先順位の高い要素を取り出すことのできるデータ構造です。

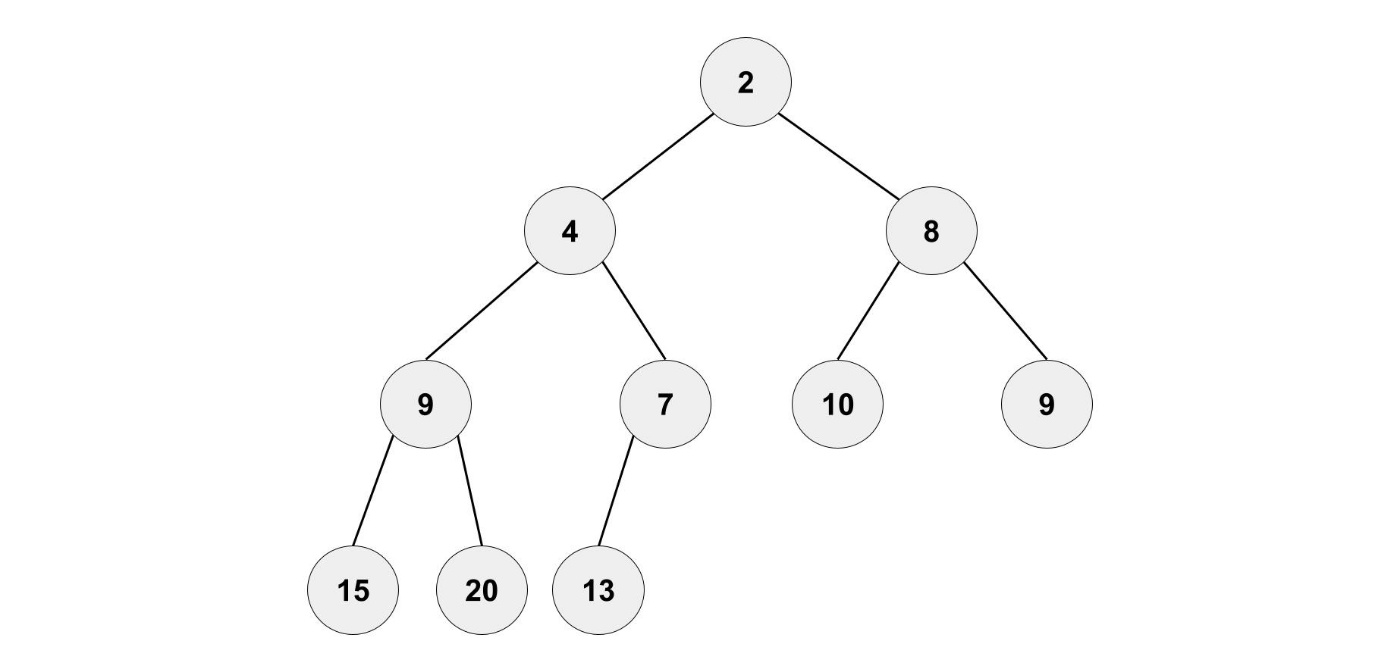
ヒープであるには、以下の条件を満たす必要があります。

深さ h-1 まではバランスが取れている、深さ h では，左側にノードが詰められている。
「親の要素」 ≦ 「子の要素」となっている。

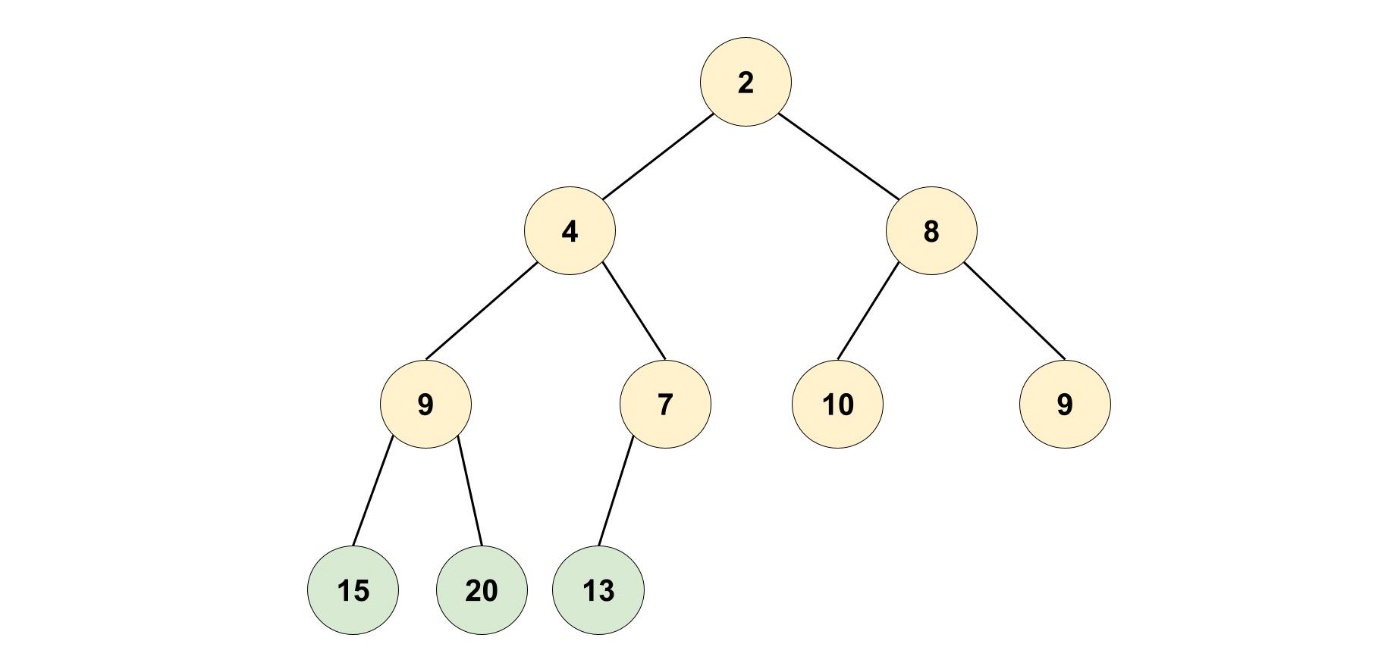
まずは、最小の要素を取り出してみます。
その後、最後の要素をルートノードに持ってきます。

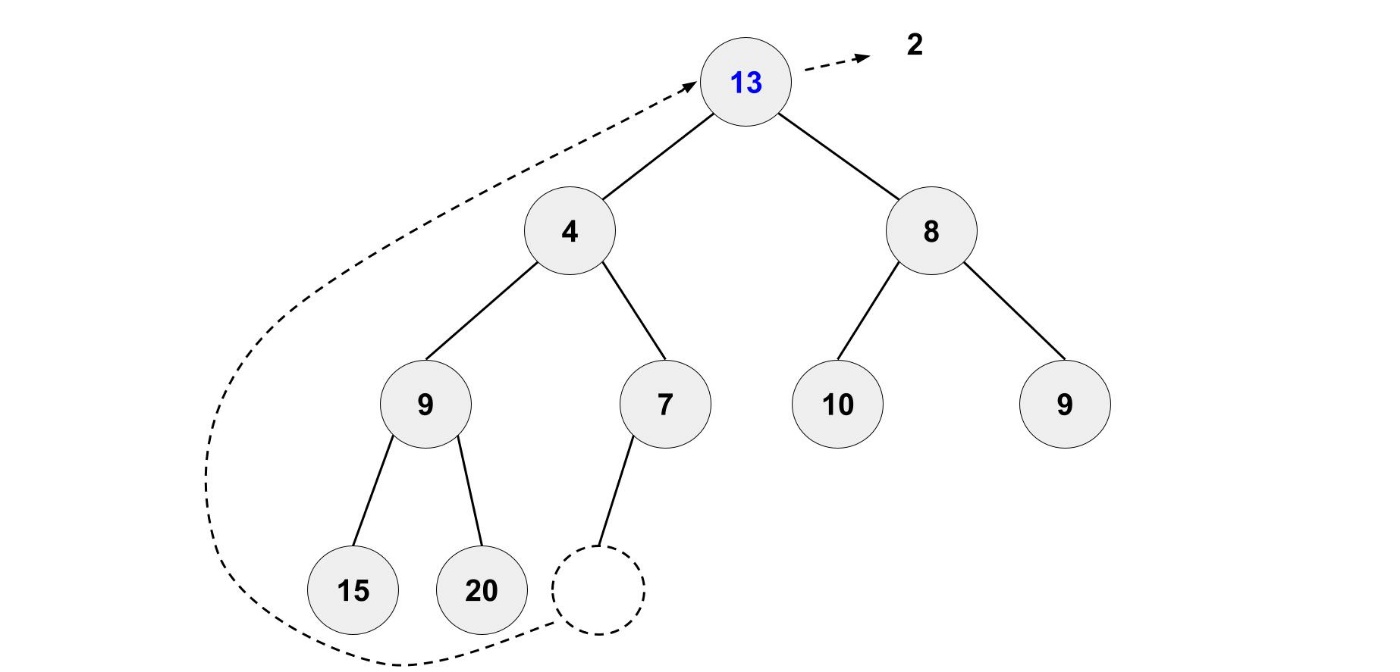
もちろん、このままにするのではなく正しい位置に移動させます。
左右の子ノードを比較して、小さい方と位置を入れ替えます。
これを繰り返すことで、ヒープの条件を満たすようになります。

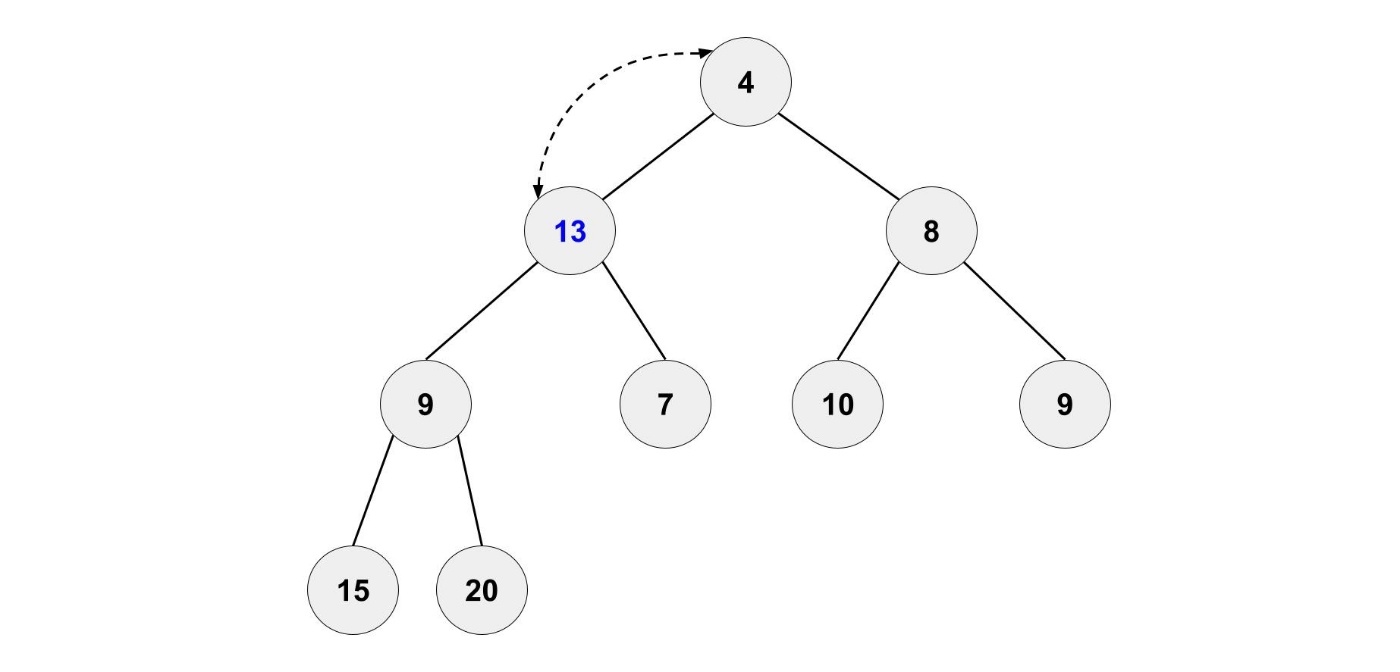
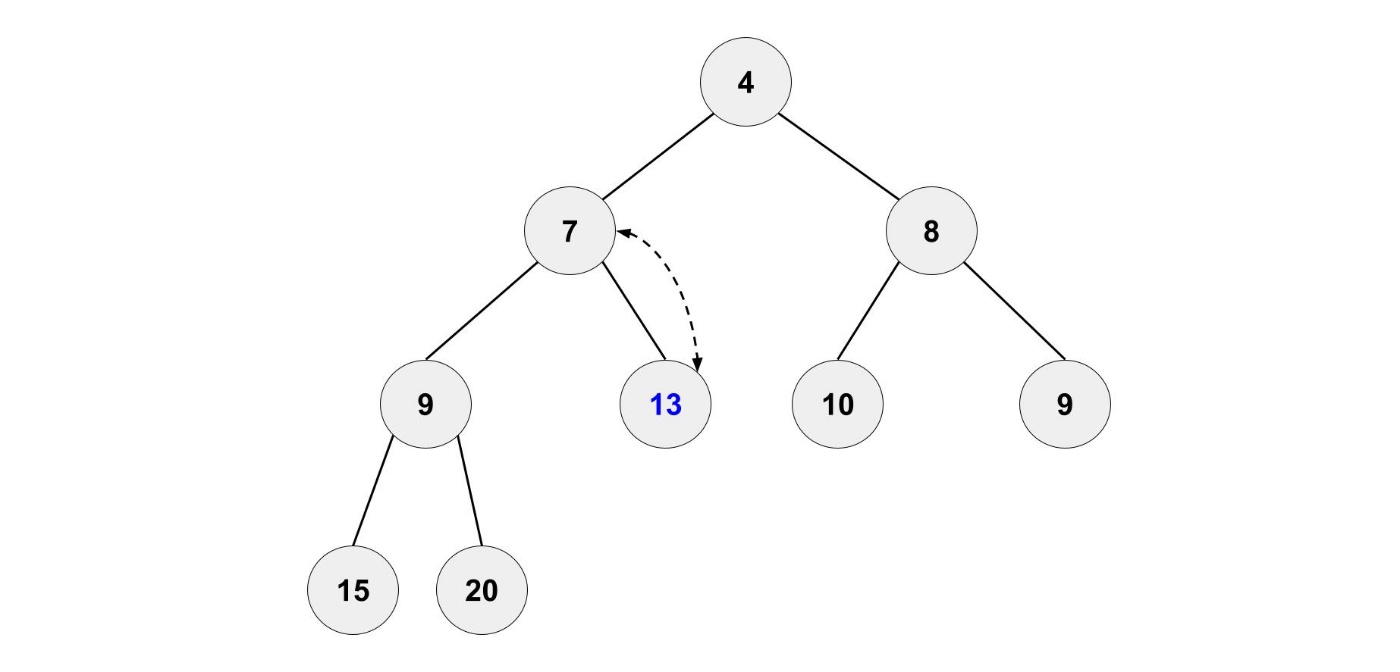
新しい要素を追加するのも簡単です。
一番最後に新しい要素を追加します。

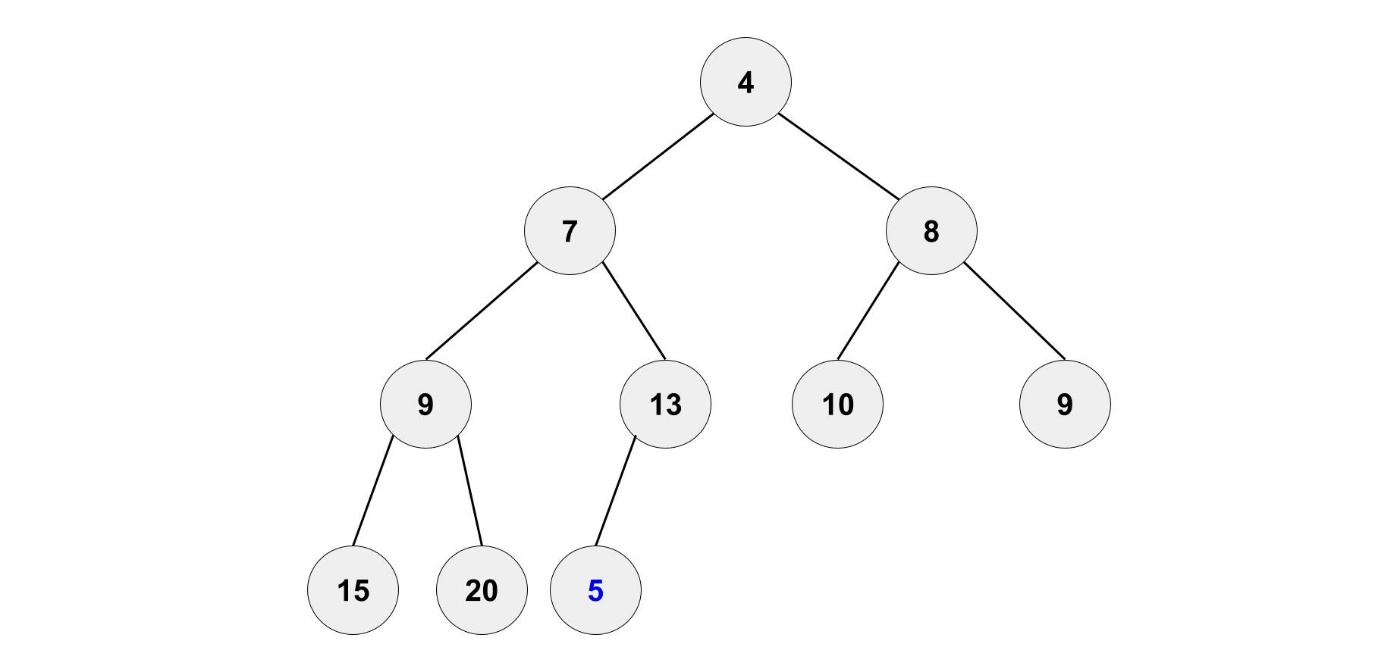
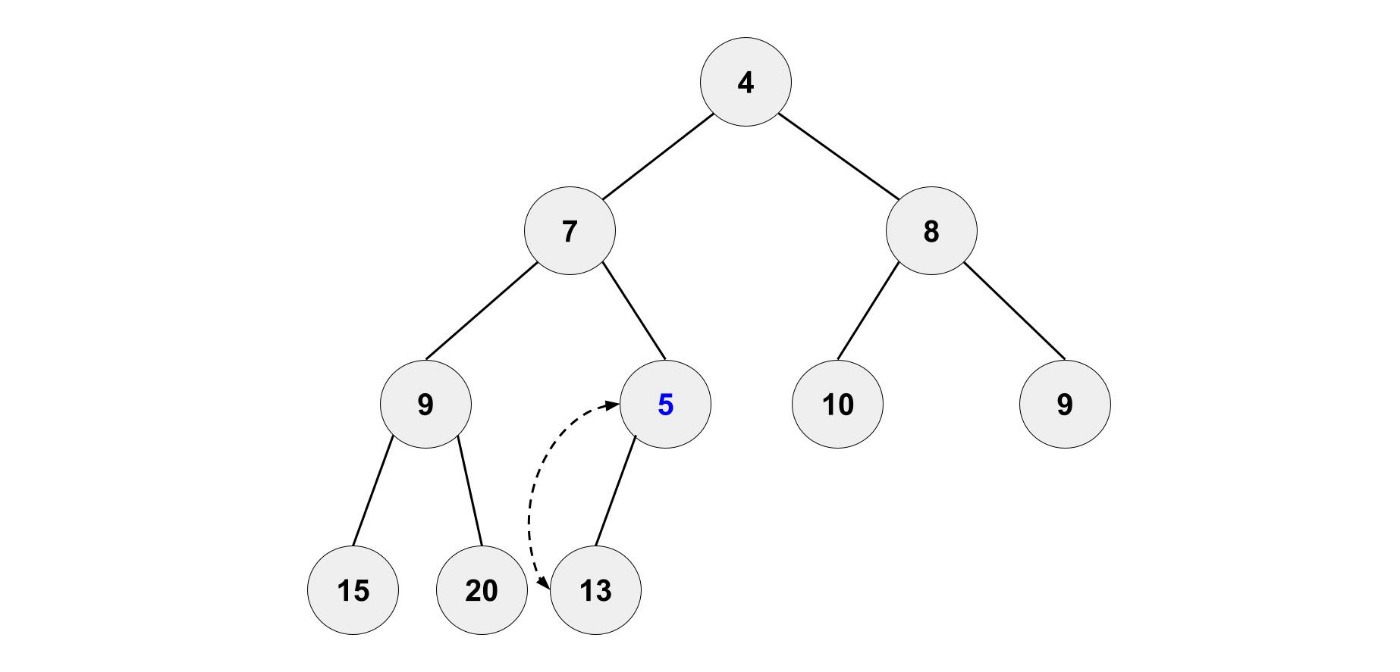
もちろん、このままにするのではなく正しい位置に移動させます。
新しい要素を親と比較して、親の要素より小さい場合は位置を入れ替えます。
これを繰り返すことで、ヒープの条件を満たすようになります。

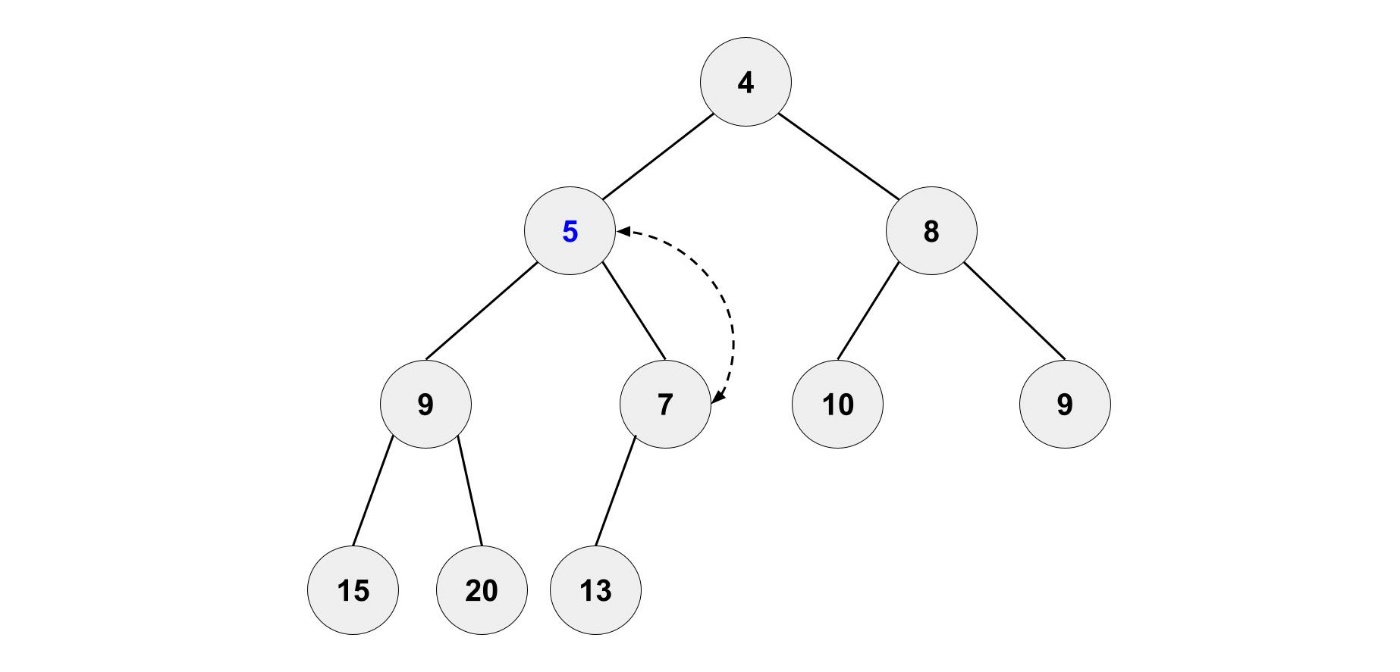
まとめ

以上で、コーディングテストを突破するために、大切なアルゴリズムやデータ構造は大体把握できたと思います。

残念ながら、アルゴリズムを知っているだけでは、コーディングテストは突破できないと思います。
コーディングテストを突破するためには、時間内に問題を解く練習が必要です。

最低限の数学についての知識がある
使い慣れているプログラミング言語がある
基本的なアルゴリズムを理解している
練習問題を解き慣れている

練習問題を解くことで、スピードと精度をアップさせて行きましょう！

参考資料

コーディング面接対策のために解きたいLeetCode 60問

ここにあるようなコンセプトを網羅できるように、アルゴリズムとデータ構造を選択させていただきました。

Grokking Algorithms

どのような順番でアルゴリズムとデータ構造を説明すると分かりやすいのか参考にさせていただきました。

導入

1. 二分探索

Binary search (二分探索)

Big O記法

2. 選択ソート

配列と連結リスト

配列と連結リストの比較

Selection Sort (選択ソート)

3. 再帰

Recursion (再帰)

Stack (スタック)

4. クイックソート

分割統治法

Quicksort (クイックソート)

5. ハッシュテーブル

ハッシュ関数

Hash Tables (ハッシュテーブル)

6. 幅優先探索

グラフとは?

Breadth-first search (幅優先探索)

Queue (キュー)

7. ダイクストラ法

重み付きグラフ

Dijkstra’s algorithm (ダイクストラ法)

8. 貪欲法

スケジューリング問題

ナップサック問題

集合被覆問題

巡回セールスマン問題

NP完全問題を見抜く方法

9. 動的計画法

ナップサック問題

10. 二分探索木

Binary search tree (二分探索木)

Heap (ヒープ)

まとめ

参考資料

Discussion