【ML Paper】DeiT: There are only fewer images for ViT? Part3

The summary of this paper, part3.
The authors proposed an improved Vision Transformer, DeiT(Data-Efficient image Transformer)

Original Paper: https://arxiv.org/abs/2012.12877v2

3. Distillation through attention

3.1 Soft distillation

Soft distillation minimizes the Kullback-Leibler divergence between the softmax of the teacher and the softmax of the student model.

The Loss is:
$\mathcal{L}_\text{global} = (1 - \lambda) \mathcal{L}_\text{CE} (\psi(Z_s), y) + \lambda \tau^2 KL (\psi(Z_s / \tau), \psi(Z_t / \tau))$

Where
$\mathcal{L}:$ Loss
$\lambda:$ The coefficient balancing the Kullback–Leibler divergence loss (KL) and the cross-entropy (LCE) on
ground truth labels y
$CE:$ CrossEntropy
$\psi:$ Softmax function
$Z_s:$ The logits of the student model
$Z_t:$ The logits of the teacher model
$KL:$ Kullback-Leibler divergence loss
$\tau:$ The temperature for the distillation

3.2 Hard-label distillation

They introduce a variant of distillation where they take the hard decision of the teacher as a true label. Let $y_t = argmax_c Z_t(c)$ be the hard decision of the teacher.

The Loss is:
$\mathcal{L}^\text{hardDistill}_\text{global} = \dfrac{1}{2} \mathcal{L}_\text{CE} (\psi(Z_s), y) + \dfrac{1}{2} \mathcal{L}_\text{CE} (\psi(Z_s), y_t)$

$y_t: \argmax_c Z_t(c)$

Use the teacher's prediction to answer CE loss as like auxilially loss.

For a given image, the hard label associated with the teacher may change depending on the specific data augmentation. We will see that this choice is better than the traditional one, while being parameter-free and conceptually simpler: The teacher prediction $y_t$ plays the same role as the true label $y$.
Note also that the hard labels can also be converted into soft labels with label smoothing, where the true label is considered to have a probability of $1 − \epsilon$, and the remaining $\epsilon$ is shared across the remaining classes. We fix this parameter to $\epsilon = 0.1$ in our all experiments that use true labels.

3.3 Distillation token

They add a new token, the distillation token, to the initial embeddings.
Their distillation token is used similarly as the class token: it interacts with other embeddings through self-attention, and is output by the network after the last layer for loss for distillation.
The distillation embedding allows our model to learn from the output of the teacher, as in a regular distillation, while remaining
complementary to the class embedding.

The average cosine similarity between these tokens is equal to 0.06. As the class and distillation embeddings are computed at each layer, they gradually become more similar through the network, and it will be 0.93 at the last layer. But still lower than 1, This is expected since as they aim at producing targets that are similar but not identical.

・Distillation token

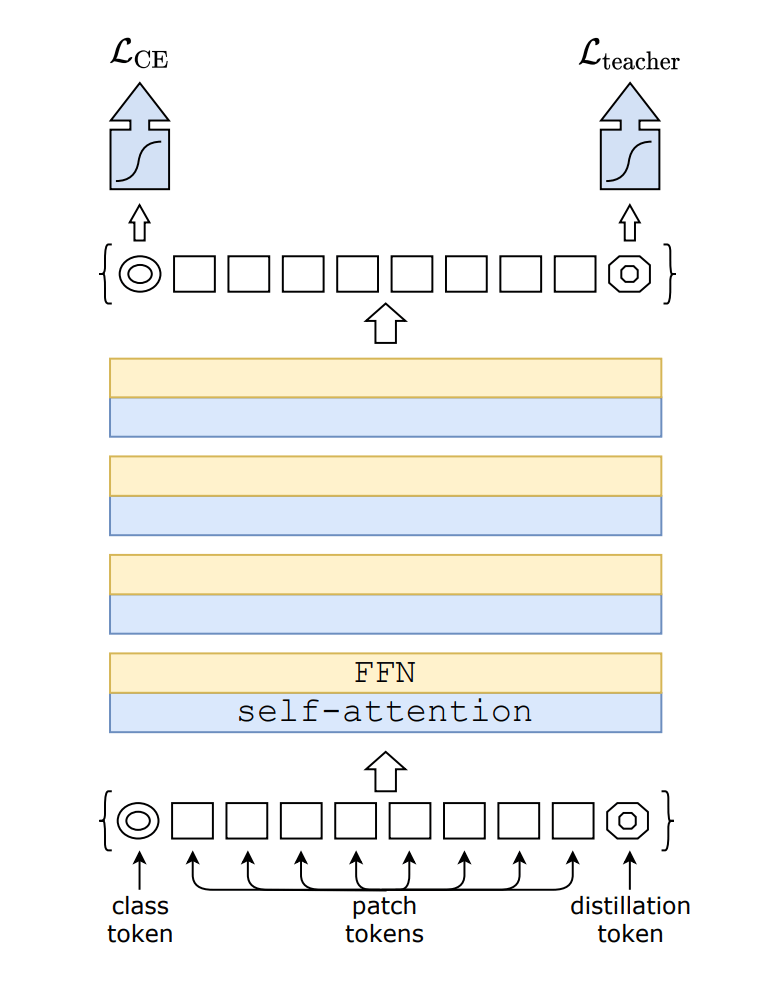
They tried adding the 2nd class token with calculate loss with true label $y$, not the teacher model's $y_t$, but the 2 class tokens are almost the same vector(cos=0.999) and didn't contribute to the performance.
In contrast, it shows their distillation strategy provides a improvement over a vanilla distillation baseline.

3.4 When fine-tuning

Use both the true label and teacher's predictions during the fine-tuning stage at higher resolution. They have also tested with true labels only but this reduces the benefit of the teacher and leads to a lower performance.

3.5 Inference method: joint classifiers

At test time, both the class or the distillation embeddings produced by the transformer are associated with linear classifiers and able to infer the image label. Yet their referent method is the late fusion of these two separate heads, for which they add the softmax output by the two classifiers to make the prediction.

This is the end of this part. I'll write the next part soon.

Reference

[1] Training data-efficient image transformers & distillation through attention