【ML】Swin Transformer explained

SwinTransformer is a model that solves the problems of VisionTransformer.

Problem 1: Since the image is divided into patches of a specific size, changes in object scale cannot be captured. Both large and small dogs need to be recognized as dogs.

Problem 2: The amount of calculation increases as the image resolution increases. The amount of calculation for self-attention increases in proportion to the square of the number of patches.

Improvement point 1: The patch size is changed gradually.

Improvement point 2: Self-Attention is applied only within a limited window, not to the entire image.

・Patch merging: The size of the feature map is changed gradually.

・Swin Transformer Block: W-MSA and SW-MSA (described later) are applied alternately. The rest is a normal Transformer.

・Patch Partition: Divide the image into a fixed size like VIT

By combining the neighboring 2×2 patch features in the channel direction, the size of the feature map is reduced,

and the resulting 4𝐶-dimensional feature is converted to 2𝐶-dimensional by a fully connected layer.

This allows one patch to obtain a wider range of features (equivalent to making the patch larger).

In the Swin Transformer, by overlapping Patch Merging, the feature map is finally reduced to 𝐻/32×𝑊/32
pixels. At this time, the patch feature is 8𝐶-dimensional.

・Linear Embedding: Convert the patch feature from 4×4×3=48 dimensions to 𝐶 dimensions.

In practice, the two are combined and performed by conv2d with kernel_size=stride=patch size.

・SwinTransformer
Basically the same as the normal Transformer. Alternately applies W-MSA and SW-MSA (described below).

Window-based Multi-head Self-Attention (W-MSA)

The feature map is divided into a 𝑀×𝑀 window, and Self-Attention is calculated only on patches within the window.
The computational complexity is reduced as follows.
When there are ℎ×𝑤 patches, the computational complexity of the entire Self-Attention is as follows.
Ω 𝑀𝑆𝐴 = 4ℎ𝑤C2 +2(ℎ𝑤)2𝐶
The first term is the computational complexity of the four fully connected layers that perform the query, key, and value calculations and the final linear transformation, and the second term is the computational complexity required for the matrix multiplication between the query and the key.
In this case, the computational complexity increases according to (ℎ𝑤)2. On the other hand, the computational complexity when performing self-attention only within the 𝑀×𝑀 window is
Ω W−𝑀𝑆𝐴 = 4ℎ𝑤C2 +2M2ℎ𝑤𝐶
and when 𝑀 is fixed (default is 7), the computational complexity follows ℎ𝑤.

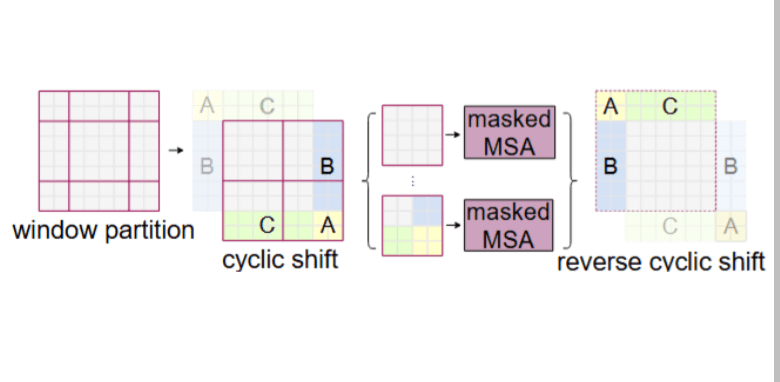
Shifted-Window-based Multi-head Self-Attention (SW-MSA)

W-MSA is performed by moving the window by (M/2,M/2) pixels.
However, if the window is simply moved, the number of windows increases and a window smaller than M×M is created.
Even if the window size is made uniform by padding, the amount of calculation increases.

Therefore, the window is fixed, and a cyclic shift is performed on the feature map, and masking (masking parts A, B, and C) is applied to windows that contain multiple windows that are not actually adjacent, and the attention between different windows is set to 0 to perform efficient calculations.
By moving the feature map instead of the window, the size and number of windows are fixed in the calculation.

Relative position bias

Unlike ViT, the Swin Transformer does not assign absolute position information to each patch feature.
Instead, by using relative position bias: 𝐵, the attention weights are adjusted according to the relative position relationship within the window when calculating Self-Attention.

The relative positional relationship within the 𝑀×𝑀 window is in the range of −𝑀+1, 𝑀−1 vertically and horizontally (from the left end as seen from the right end to the right end as seen from the left end), so there are (2𝑀−1)2 possibilities for 𝐵.