【Statistics Method】About Kolmogorov–Smirnov(K-S) test

0. Where to use?

K-S test is the method to compare the two distributions(not strict, but like that).
This method is used for various situations in statistics, but I use this in the machine learning field, to check whether the two models are similar or not(applying to the result of models).
When tackling an ensemble, that model to be merged must have diversity. So, I check the similarity of models pseudo by this if necessary.

1. What is the Kolmogorov–Smirnov (K-S) test

The Kolmogorov–Smirnov (K-S) test is a non-parametric statistical test used to determine if two samples come from the same distribution or if a sample matches a specific distribution.

Practically, the low p-value(<0.05) indicates the null hypothesis is rejected, which means the two have differences.
This is the only result that can be obtained.
Conversely, no low p-value(>=0.05) indicates that couldn't reject the null hypothesis, this suggests the two haven't difference(similar), but it's uncertain because the obtained result is only "couldn't reject the null hypothesis".
There may be differences, or not.

2. Example

2.1 Example Code

Here is the example code.

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

# Generate a sample of data
np.random.seed(42)
sample_data = np.random.normal(loc=0, scale=1, size=100)  # A sample from a normal distribution

# Perform the K-S test against a normal distribution
D, p_value = stats.kstest(sample_data, 'norm', args=(0, 1))

print(f"KS Statistic: {D}")
print(f"P-value: {p_value}")

# Interpretation
if p_value < 0.05:
    print("Reject the null hypothesis: The sample does not follow a normal distribution.")
else:
    print("Fail to reject the null hypothesis: The sample follows a normal distribution.")

# Plotting the empirical CDF vs the theoretical CDF
ecdf = np.sort(sample_data)
cdf = np.arange(1, len(ecdf) + 1) / len(ecdf)
plt.plot(ecdf, cdf, marker='.', linestyle='none', label='Empirical CDF')

# Theoretical CDF for the normal distribution
x = np.linspace(min(ecdf), max(ecdf), 100)
plt.plot(x, stats.norm.cdf(x, loc=0, scale=1), label='Theoretical CDF (Normal Dist)')

plt.legend()
plt.xlabel('Value')
plt.ylabel('CDF')
plt.title('Empirical CDF vs Theoretical CDF')
plt.show()

The point of this code is here:

D, p_value = stats.kstest(sample_data, 'norm', args=(0, 1))

・Argments
sample_data is the data to be tested.
'norm' is the distribution that is compared. The normal (Gaussian) distribution is used this time.
args provides the parameters of the normal distribution, where left(0) is the mean and right(1) is the standard deviation.

・Outputs
D(KS Statistic) is the maximum difference between the empirical and theoretical CDFs.
P-value is used to determine the statistical significance of the result.

2.2 Result

Here are the results.

KS Statistic: 0.10357070563896065
P-value: 0.21805553378516235
Fail to reject the null hypothesis: The sample follows a normal distribution.

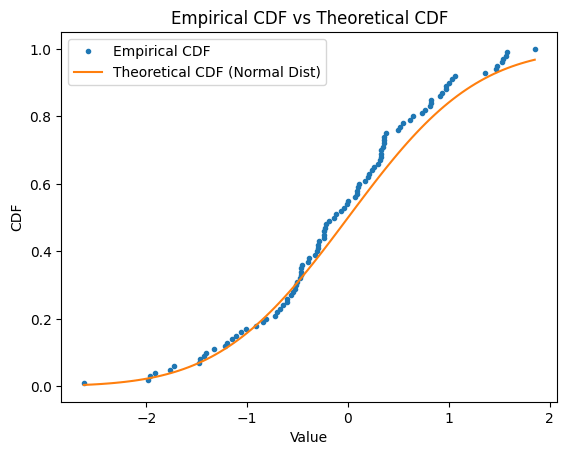
Interpretation
・KS Statistic($D$)
This is defined as the maximum absolute difference between the empirical CDF of a sample and the theoretical CDF of the distribution being tested (one-sample test), or between the empirical CDFs of two samples (two-sample test).
Formula: $D_{n,m} = \sup|F_n(x)-G_m(x)|$
※$\sup$ denotes the supremum (maximum) over all values of x.

The meaning is simple and intuitive.
-Small D
If the K-S statistic is small, it suggests that the empirical CDF of the sample is close to the theoretical CDF, meaning the sample data is likely drawn from the theoretical distribution(or two dist is similar).
-Large D
A large K-S statistic indicates a significant difference between the empirical and theoretical CDFs, suggesting that the sample data may not be from the theoretical distribution(or two dist may be different).

・P-value
If under by 0.05, indicates the distributions are different. Over 0.05, suggests the two haven't differences(similar), but it's uncertain. There may be differences, or not.
・CDF
The Cumulative Distribution Function (CDF) of a random variable
$X$ is a function that maps a value $x$ to the probability that $X$ will take a value less than or equal to $x$. In other words, it shows probability distillation of $X$.
Formula: $F(x) = P(X \geq x)$

3. Summary

Kolmogorov–Smirnov(K-S) test is the method to check the difference of two distilations or datasamples.
The inside contents are difficult, but the impremetation of python is simple, please try to use it.