🍎

Scaled Dot-Product Attentionとは (Transformerその1)

2023/11/25に公開

今回はTransformerに使用されている、Scaled Dot-Product Attentionについて解説します。
この記事を参考にして書いているため、先にこちらを見ることをお勧めします。
また、ある程度モデルについて知識のある方を対象にしています。

Transformer

初めに、Transformerのアーキテクチャは次のようになっています。

そしてこの中のMulti-head Attentionのアーキテクチャは次のようになっています。

今回はさらにこの中のScaled Dot-Product Attentionについて解説していきます。

Scaled Dot-Product Attention

Scaled Dot-Product Attentionのアーキテクチャは次のようになっています。

Scaled Dot-Product Attention

数式

Scaled Dot-Product Attentionは、基本的に次の数式で表されます。これは、上の図の操作を数式で表現したものです。
出力(output) = $softmax(\dfrac{QK^T}{\sqrt{d_k}})V$

Q: query(入力)
K: key(入力)
V: value(入力)
$d_k$ : keyのベクトルの次元数(Scale)
softmax: 正規化関数

初めに、この数式を理解するところから始めます。

Matmul( $QK^T$ )

行列 $Q$ と $K^T$ (転置)の行列積

MatMulレイヤでは行列積演算を行なっています。ここでは、 $Q$ の行列と $K$ の行列の行列積を行なっていますが、まずは $q$ ベクトル と $K$ 行列 の行列積だと考えた方が理解しやすいです。

次の図を見て下さい。

$q$ ベクトルと $K$ 行列の行列積はこのように可視化され、この結果、

$q・K=[1,30,4,9,2]$

のような、「 $K$ 行列の各ベクトルがどの程度 $q$ ベクトルと類似しているか」を示す行列(重みベクトル)が作成されます。

そして、これが(ベクトルでなく) $Q$ 行列に対して行われると、 $Q$ 行列の全ベクトルと、 $K$ 行列の各ベクトルの類似度を表す行列が作成されます。
イメージとしては、

$Q・K =$
$[1,30,4,9,2]$ # $Q$ 行列の1行目と $K$ 行列の(各列についての)類似度
$[1,3,20,9,2]$ # $Q$ 行列の2行目と $K$ 行列の(各列についての)類似度
$[15,3,7,1,6]$ # $Q$ 行列の3行目と $K$ 行列の(各列についての)類似度
$...$

のように、 $Q$ の全ての行について、 $K$ 行列との類似度をとった行列が作成されます。

つまり、 $QK^T$ は $Q$ 行列と $K$ 行列の各ベクトルの類似度を示す行列を作成する操作です。

Scaled

正規化 $\dfrac{QK^T}{\sqrt{d_k}}$

Scaledレイヤでは、正規化を行なっています。

$QK^T$ は、将来的に重みとして使用するために、 $Q$ 行列のベクトルと $K$ 行列のベクトルの類似度を求めることを目的にしています。

ですが、行列積はベクトルの次元数が多いほど、(当然ですが)出力結果が大きくなる特性を持ちます。これによって類似度計算後のsoftmaxの出力が極端(1要素以外ほぼ0)になってしまったり、勾配情報が消失するといった問題が発生します。
そこで、 $K$ 行列のベクトルの次元数の平方根で出力結果を除算することで、正規化を行い次元数による影響を回避して、適切に類似度を表現できるようにしています。

Mask(opt.)

マスク(オプション)

Maskではマスクをおこなっています。

これは主に出力生成時の推測(prediction)および訓練(train)時に行われる操作で、一般的には下三角行列と内積を取ることで未来の情報を利用できなくします。

下三角行列(要素を全て1としている)

[[1, 0, 0, 0, 0],
 [1, 1, 0, 0, 0],
 [1, 1, 1, 0, 0],
 [1, 1, 1, 1, 0],
 [1, 1, 1, 1, 1]]

例えば、[i have a pen .] という時系列データがあった場合、[i]の次の単語を予測するタスクでは、[have a pen .]という情報は答えにあたるため、提供されてはいけないはずです。

そこで、予測時には下三角行列を使用して次のような行列を入力とします。

[['i', '0', '0', '0', '0'],
 ['i', 'have', '0', '0', '0'],
 ['i', 'have', 'a', '0', '0'],
 ['i', 'have', 'a', 'pen', '0'],
 ['i', 'have', 'a', 'pen', '.']]

これを上から順に入力することで、未来の情報を知ることなく、適切に予測を行えるようになります。

また、異なる長さのデータについて、長さを揃えるためにマスクを使用したり、訓練時にも未来の情報を使用して推論を行うモデルになることを避けるためにマスクを行うことがあります。

softmax

正規化

softmaxレイヤでは、正規化を行なっています。
上記で求めた $Q$ の各ベクトルと $K$ 行列の類似度に、最大値1の正規化を行なって重みとして利用できるようにします。

softmax

$\dfrac{QK^T}{\sqrt{d_k}} =$
$[1.1, 2.0, 0.2, 1.1, -1.2]$
$[1.5, 3, 2, 0.4, 1]$
$[1.2, 2, 0.2, 0.2, 0.8]$
$...$

↓softmax(正規化)

$softmax(\dfrac{QK^T}{\sqrt{d_k}}) =$
$[0.20, 0.50, 0.08, 0.20, 0.02]$
$[0.12, 0.55, 0.20, 0.04 0.08]$
$[0.22, 0.48, 0.08, 0.08, 0.15]$
$...$

Matmul( $softmax(\dfrac{QK^T}{\sqrt{d_k}})V$ )

行列積

これまでに作ってきた $Q$ 行列と $K$ 行列の類似度と、 $V$ 行列の行列積を取ります。
ここでも初めはベクトルで考えましょう。

例えば
$softmax(\dfrac{qK^T}{\sqrt{d_k}})=[0.20, 0.50, 0.08, 0.20, 0.02]$
とすると、これは $q$ に対して、 $K$ 行列の2行目が一番似ていることを示しています。
(分からない人は最初のMatMulの説明を確認してみて下さい)

これと $V$ の行列積を取ります。

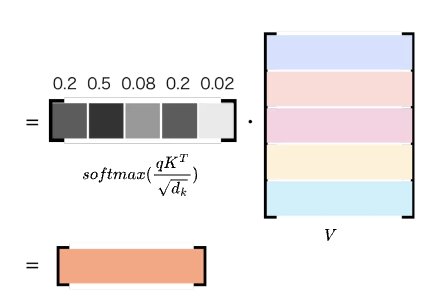
図を見ると、 $V$ の2行目の成分がより多く抽出されることが分かります。
これはつまり、 $q$ と $K$ を比較して、似ている行を見つけ出し、重みとします。そして、この重みを利用して、 $q$ と $K$ が似ている行について、より多く $V$ の要素を取得しています。

これがScaled Dot-Product Attentionの最終出力です。(本来は $Q$ なので行列が出力されます)

具体例

具体的に翻訳タスクで考えます。
Transformerではself-Attentionが使用されるため、 $Q$ と $K$ と $V$ は全て(全結合層を通る前は)同じ入力です。

初めに $Q$ によって、各単語(ベクトル)と $K$ で保持している全ての単語(ベクトル)の類似度を計算します。ここで、 $K$ は入力文章を保持する役割を担っています。
そして、例えば $Q$ 行列の1行目( $q$ ベクトル)が[I]だった場合、 $Matmul(qK^T)$ によって[am]や[you]など似ている列の値が大きくなる重みベクトルを作成します。
その重みを使用して、関連度の高い情報を $V$ から抽出し、予測に利用します。つまり、予測に必要な情報に注目して、それを予測に利用することができるのです。

擬似コードでも流れを確認して見ましょう。(本来はembeddingによって単語はベクトル化されていますが、視認性向上のためそのまま記述しています)

# 擬似コード
Q = [[I,
      am,
      fine,
      .,
      And,
      you]
q = [I]
K = [[I, am, fine, ., And, you]]
V = [[I,
      am,
      fine,
      .,
      And,
      you]
# 類似度を計算
weight = q・K  # =[0.7, 0.11 , 0.03, 0.03, 0.03, 0.1]
# Vから、[I]に似た情報を抜き出す
output = weight・V # I, am, youの単語ベクトルの情報を多く含む

結論

Scaled Dot-Product Attentionは、スケーリングや行列積を利用して、 $Q$ について $K$ と似ている部分の情報を、 $V$ から抽出する手法でした。

これによって、時系列データ同士の関連度を取得したり、予測する際に関連度の高い情報を利用できるようになります。

また、 $Q$ 行列を異なる行列にしたものをSource Traget Attentionと呼びます。(例えば[i]ではなく[she]のような、 $K$ , $Q$ 行列に含まれない単語と、[I, am, fine, ., And, you]のそれぞれとの関連度を取得できる)

Tarnsformerは6年前に発表された技術ですが、最近のモデルもTransformerを利用しているものが多く、現在でもとても重要な技術です。
それでは、今回は以上です。最後まで読んでいただきありがとうございました。

参考

[1]https://arxiv.org/pdf/1706.03762.pdf
[2]https://developers.agirobots.com/jp/multi-head-attention/