機械学習モデル作成シリーズ Step5 データの前処理
機械学習モデル作成のStep5です。前回はロードしたデータを確認する方法について扱いました。
続いて今回はデータの前処理を解説します。
5 データの前処理
ロードしたデータを学習に使用する前に、前処理を行う必要があります。前処理とは、データをモデルが学習しやすいように加工することです。
欠損値処理や正規化、データ拡張など多岐に渡ります。
今回はこれら前処理について、一般的に処理を行う順番に沿って解説しています。
5.0 データのロード
学習に使用するデータをロードします。
5.1 欠損値処理
欠損値の置換、削除、または回帰補完、多重補完などを行います。
ここでは簡単な置換と削除を紹介します。
※単純な置換はデータによっては不適切な場合があります。
5.1.1 .fillna(value, method)
fillna()は欠損値を別の値に置き換えます。
固定値で置き換える方法(value)と、上下の値をコピーして置き換える方法(method)があります。
fillna(value)
# fillna()
import pandas as pd
import numpy as np
data = {'A': [1, np.nan, 3, 4, 5],
'B': [np.nan, 7, 8, np.nan, 10],
'C': [11, 12, np.nan, 15, np.nan],
'D': [np.nan, np.nan, np.nan, np.nan, np.nan]
}
df = pd.DataFrame(data)
print(df)
# 出力
# A B C D
# 0 1.0 NaN 11.0 NaN
# 1 NaN 7.0 12.0 NaN
# 2 3.0 8.0 NaN NaN
# 3 4.0 NaN 15.0 NaN
# 4 5.0 10.0 NaN NaN
## 欠損値を固定値(value)で置き換える
# 欠損値を0で置き換える
print(df.fillna(value=0))
# 出力
# A B C D
# 0 1.0 0.0 11.0 0.0
# 1 0.0 7.0 12.0 0.0
# 2 3.0 8.0 0.0 0.0
# 3 4.0 0.0 15.0 0.0
# 4 5.0 10.0 0.0 0.0
# A行の欠損値を5、B行の欠損値を3で置き換える
print(df.fillna({"A":5, "B":3}))
# 出力
# A B C D
# 0 1.0 3.0 11.0 NaN
# 1 5.0 7.0 12.0 NaN
# 2 3.0 8.0 NaN NaN
# 3 4.0 3.0 15.0 NaN
# 4 5.0 10.0 NaN NaN
# 欠損値を各列の平均値に置き換える
print(df.fillna(df.mean()))
# 出力
# A B C D
# 0 1.00 8.333333 11.000000 NaN
# 1 3.25 7.000000 12.000000 NaN
# 2 3.00 8.000000 12.666667 NaN
# 3 4.00 8.333333 15.000000 NaN
# 4 5.00 10.000000 12.666667 NaN
fillna(method)
## 欠損値を上下の値のコピーで置き換える
# 上の値で欠損値を埋める(最初の行には欠損値が残る)
print(df.fillna(method='ffill'))
# 出力
# A B C D
# 0 1.0 NaN 11.0 NaN
# 1 1.0 7.0 12.0 NaN
# 2 3.0 8.0 12.0 NaN
# 3 4.0 8.0 15.0 NaN
# 4 5.0 10.0 15.0 NaN
# 下の値で欠損値を埋める(最後の行には欠損値が残る)
print(df.fillna(method='bfill'))
# 出力
# A B C D
# 0 1.0 7.0 11.0 NaN
# 1 3.0 7.0 12.0 NaN
# 2 3.0 8.0 15.0 NaN
# 3 4.0 10.0 15.0 NaN
# 4 5.0 10.0 NaN NaN
5.1.2 .dropna()
dropna()は1つでも欠損値を含む行、列を削除します。
dropna(how='all')の場合、値が全て欠損値の行、列のみを削除します。
dropna()
# dropna()
import pandas as pd
import numpy as np
data = {'A': [1, np.nan, 3, 4, 5],
'B': [np.nan, 7, 8, np.nan, 10],
'C': [11, 12, 13, 14, 15],
'D': [np.nan, np.nan, np.nan, np.nan, 20]
}
df = pd.DataFrame(data)
print(df)
# 出力
# A B C D
# 0 1.0 NaN 11 NaN
# 1 NaN 7.0 12 NaN
# 2 3.0 8.0 13 NaN
# 3 4.0 NaN 14 NaN
# 4 5.0 10.0 15 20.0
# 欠損値を含む行をすべて削除
print(df.dropna())
# 出力
# A B C D
# 4 5.0 10.0 15 20.0
# 欠損値を含む列をすべて削除
print(df.dropna(axis=1))
# 出力
# C
# 0 11
# 1 12
# 2 13
# 3 14
# 4 15
dropna(how=all)
data = {'A': [1, np.nan, 3, np.nan, 5],
'B': [np.nan, 7, 8, np.nan, 10],
'C': [11, 12, 13, np.nan, 15],
'D': [np.nan, np.nan, np.nan, np.nan, np.nan]
}
df = pd.DataFrame(data)
print(df)
# 出力
# A B C D
# 0 1.0 NaN 11.0 NaN
# 1 NaN 7.0 12.0 NaN
# 2 3.0 8.0 13.0 NaN
# 3 NaN NaN NaN NaN
# 4 5.0 10.0 15.0 NaN
# 全て欠損値の行のみを削除
print(df.dropna(how='all'))
# 出力
# A B C D
# 0 1.0 NaN 11.0 NaN
# 1 NaN 7.0 12.0 NaN
# 2 3.0 8.0 13.0 NaN
# 4 5.0 10.0 15.0 NaN
# 全て欠損値の列のみを削除
print(df.dropna(axis=1, how='all'))
# 出力
# A B C
# 0 1.0 NaN 11.0
# 1 NaN 7.0 12.0
# 2 3.0 8.0 13.0
# 3 NaN NaN NaN
# 4 5.0 10.0 15.0
5.2 データの統合
必要に応じて、異なるデータソースからのデータを統合し、適切な形式に変換します。
ここではDataFrameの統合手法であるmerge(), concat(), join()についてそれぞれ解説します。
5.2.1 merge()
merge()は列の値もしくはインデックスを基準にして、2つ以上のDataFrameを結合します。
結合には内部結合、外部結合、左結合、右結合があります。
1. 内部結合
基準列に共通のデータを持つ行のみ保持します。
# merge()
# 内部結合
import pandas as pd
# 2つのデータフレームを作成
df1 = pd.DataFrame({'alpha': ['A', 'B', 'C'], 'value1': [1, 2, 3]})
df2 = pd.DataFrame({'alpha': ['B', 'C', 'D'], 'value2': [4, 5, 6]})
# df1
# alpha value1
# 0 A 1
# 1 B 2
# 2 C 3
# df2
# alpha value2
# 0 B 4
# 1 C 5
# 2 D 6
# alpha列を基にしてdf1とdf2を内部結合
merged_inner = pd.merge(df1, df2, on='alpha')
print(merged_inner)
# 出力
# alpha value1 value2
# 0 B 2 4
# 1 C 3 5
# 行インデックスを基準にして内部結合
merged_inner = pd.merge(df1, df2, left_index=True, right_index=True)
print(merged_inner)
# 出力
# alpha_x value1 alpha_y value2
# 0 A 1 B 4
# 1 B 2 C 5
# 2 C 3 D 6
# ※(suffixes=['_left', '_right'])で同じ列名の末尾を指定できる
# alpha_left value1 alpha_right value2
# 2つのデータフレームを作成
df1 = pd.DataFrame({'alpha': ['A', 'B', 'C'], 'value1': [1, 2, 3]})
df2 = pd.DataFrame({'alphabet': ['B', 'C', 'D'], 'value2': [4, 5, 6]})
# df1
# alpha value1
# 0 A 1
# 1 B 2
# 2 C 3
# df2
# alpha value2
# 0 B 4
# 1 C 5
# 2 D 6
# alpha列とalphabet列を基準にdf1とdf2を内部結合
merged_inner = pd.merge(df1, df2, left_on='alpha', right_on="alphabet")
print(merged_inner)
# 出力
# alpha value1 alphabet value2
# 0 B 2 B 4
# 1 C 3 C 5
# 左行列のvalue1列と右行列のインデックスを基準に内部結合
merged_inner = pd.merge(df1, df2, left_on='value1', right_index=True)
print(merged_inner)
# 出力
# alpha value1 alphabet value2
# 0 A 1 C 5
# 1 B 2 D 6
2. 左結合
左側の行列のデータを保持します
# merge()
# 左結合
import pandas as pd
# 2つのデータフレームを作成
df1 = pd.DataFrame({'alpha': ['A', 'B', 'C'], 'value1': [1, 2, 3]})
df2 = pd.DataFrame({'alpha': ['B', 'C', 'D'], 'value2': [4, 5, 6]})
# df1
# alpha value1
# 0 A 1
# 1 B 2
# 2 C 3
# df2
# alpha value2
# 0 B 4
# 1 C 5
# 2 D 6
# 左結合: 左側行列のデータを全て残す
left_joined = pd.merge(df1, df2, on='alpha', how='left')
print(left_joined)
# 出力
# alpha value1 value2
# 0 A 1 NaN
# 1 B 2 4.0
# 2 C 3 5.0
3. 右結合
右側の行列のデータを保持します。
# df1
# alpha value1
# 0 A 1
# 1 B 2
# 2 C 3
# df2
# alpha value2
# 0 B 4
# 1 C 5
# 2 D 6
# 右結合: 右側行列のデータを全て残す
right_joined = pd.merge(df1, df2, on='alpha', how='right')
print(right_joined)
# 出力
# alpha value1 value2
# 0 B 2.0 4
# 1 C 3.0 5
# 2 D NaN 6
4. 外部結合
すべてのデータを保持します。
# df1
# alpha value1
# 0 A 1
# 1 B 2
# 2 C 3
# df2
# alpha value2
# 0 B 4
# 1 C 5
# 2 D 6
# 外部結合(完全結合): すべてのデータを残す
full_joined = pd.merge(df1, df2, on='alpha', how='outer')
print(full_joined)
# 出力
# alpha value1 value2
# 0 A 1.0 NaN
# 1 B 2.0 4.0
# 2 C 3.0 5.0
# 3 D NaN 6.0
5. 交差結合
左右の行列で作れる組み合わせを全て作成します。
生成される行列の行数は、「左行列の行数×右行列の行数」になります。
# df1
# alpha value1
# 0 A 1
# 1 B 2
# 2 C 3
# df2
# alpha value2
# 0 B 4
# 1 C 5
# 2 D 6
# 交差結合: 左右の行列で作れる、全組み合わせを生成
cross_joined = pd.merge(df1, df2, how='cross')
print(cross_joined)
# 出力
# alpha_x value1 alpha_y value2
# 0 A 1 B 4
# 1 A 1 C 5
# 2 A 1 D 6
# 3 B 2 B 4
# 4 B 2 C 5
# 5 B 2 D 6
# 6 C 3 B 4
# 7 C 3 C 5
# 8 C 3 D 6
5.2.2 concat()
concat()は2つ以上のDataFrameを単純に繋げます。縦か横に連結できます。
繋げるDataFrameはリストなどでまとめて与えます。
1. 縦に連結
単純に縦に連結します。列名が同じものは1列に統合されます。
# concat()
import pandas as pd
# 2つのデータフレームを作成
df1 = pd.DataFrame({'alpha': ['A', 'B', 'C'], 'value1': [1, 2, 3]})
df2 = pd.DataFrame({'alpha': ['B', 'C', 'D'], 'value2': [4, 5, 6]})
# df1
# alpha value1
# 0 A 1
# 1 B 2
# 2 C 3
# df2
# alpha value2
# 0 B 4
# 1 C 5
# 2 D 6
# 縦に連結する
concatenated = pd.concat([df1, df2], axis=0)
print(concatenated)
# 出力
# alpha value1 value2
# 0 A 1.0 NaN
# 1 B 2.0 NaN
# 2 C 3.0 NaN
# 0 B NaN 4.0
# 1 C NaN 5.0
# 2 D NaN 6.0
2. 横に連結
単純に横に結合します。インデックスが同じ場合は統合されます。
# df1
# alpha value1
# 0 A 1
# 1 B 2
# 2 C 3
# df2
# alpha value2
# 0 B 4
# 1 C 5
# 2 D 6
# 横に連結する
concatenated = pd.concat([df1, df2], axis=1)
print(concatenated)
# 出力
# alpha value1 alpha value2
# 0 A 1 B 4
# 1 B 2 C 5
# 2 C 3 D 6
3. 異なるインデックスを持つ場合
問題なく結合できます。
# df1
# alpha value1
# 0 A 1
# 1 B 2
# 2 C 3
# df2
# alpha value2
# 0 B 4
# 1 C 5
# 2 D 6
# df2のインデックスを変更
df2.index = [10, 11, 12]
# 縦に連結する
concatenated = pd.concat([df1, df2], axis=0)
print(concatenated)
# 出力
# alpha value1 value2
# 0 A 1.0 NaN
# 1 B 2.0 NaN
# 2 C 3.0 NaN
# 10 B NaN 4.0
# 11 C NaN 5.0
# 12 D NaN 6.0
# 横に連結する
concatenated = pd.concat([df1, df2], axis=1)
print(concatenated)
# 出力
# alpha value1 alpha value2
# 0 A 1.0 NaN NaN
# 1 B 2.0 NaN NaN
# 2 C 3.0 NaN NaN
# 10 NaN NaN B 4.0
# 11 NaN NaN C 5.0
# 12 NaN NaN D 6.0
5.2.3 join()
join()は単純なインデックスベースの結合を行います。
join()で可能な操作は全てmerge()でも行うことができますが、単純にインデックスを基準とした結合を行う際の簡易性が利点となります。
※join()はデフォルトが左結合です。(merge()は内部結合)
1. joinによる結合
import pandas as pd
# 2つのデータフレームを作成
df1 = pd.DataFrame({'alpha': ['A', 'B', 'C'], 'value1': [1, 2, 3]})
df2 = pd.DataFrame({'alpha': ['B', 'C', 'D'], 'value2': [4, 5, 6]})
# df1
# alpha value1
# 0 A 1
# 1 B 2
# 2 C 3
# df2
# alpha value2
# 0 B 4
# 1 C 5
# 2 D 6
# df1のインデックスを基にdf2を左結合
joined_left = df1.join(df2, rsuffix='_right')
print(joined_left)
# 出力
# alpha value1 alpha_right value2
# 0 A 1 B 4
# 1 B 2 C 5
# 2 C 3 D 6
5.3 データの形状変更
データを利用しやすい形状に変更します。
用意されているデータセットは、基本的に利用しやすい形状になっているため、使用頻度はそこまで多くありません。
基本の pivot(), stack(), unstack(), melt() を以下に示すので、興味のある方は確認してみて下さい。
データ形状変更 pivot(), stack(), unstack(), melt()
import pandas as pd
# ピボット操作のデータ例
data = {'date': ['2021-01-01', '2021-01-01', '2021-01-02', '2021-01-02'],
'variable': ['A', 'B', 'A', 'B'],
'value': [100, 200, 150, 250]}
df = pd.DataFrame(data)
print(df)
# 出力
# date variable value
# 0 2021-01-01 A 100
# 1 2021-01-01 B 200
# 2 2021-01-02 A 150
# 3 2021-01-02 B 250
# pivot(): ピボット操作。ピボットテーブルに変換
pivot_df = df.pivot(index='date', columns='variable', values='value')
print(pivot_df)
# 出力
# variable A B
# date
# 2021-01-01 100 200
# 2021-01-02 150 250
# stack(): スタック操作。データを縦方向に伸ばす
stacked_df = pivot_df.stack()
print(stacked_df)
# 出力
# date variable
# 2021-01-01 A 100
# B 200
# 2021-01-02 A 150
# B 250
# unstack(): アンスタック操作。多重インデックスを持つデータの、特定の列をカラムに指定してデータの横幅を広げる
unstacked_df = stacked_df.unstack()
print(unstacked_df)
# 出力
# variable A B
# date
# 2021-01-01 100 200
# 2021-01-02 150 250
# melt: メルト操作。id_varsに指定した列を基準として、'variable'に元の列名、'value'列に元の値を持つ縦方向のDataFrameを生成する
melted_df = pd.melt(df, id_vars=['date'], value_name='value_')
print(melted_df)
# 出力
# date variable value_
# 0 2021-01-01 variable A
# 1 2021-01-01 variable B
# 2 2021-01-02 variable A
# 3 2021-01-02 variable B
# 4 2021-01-01 value 100
# 5 2021-01-01 value 200
# 6 2021-01-02 value 150
# 7 2021-01-02 value 250
5.4 エンコーディング
カテゴリカル変数を数値に変換するためのエンコーディングを行います。
エンコーディングとは、文字列データなどを(機械が理解できる)数字データに変更する操作のことです。
ここではよく利用されるone-hot encodingを紹介します。
各データに対して配列を作成し、データを一意の配列に置き換えます。
・one-hot encoding
import pandas as pd
data = {
'category': ['Red', 'Blue', 'Green', 'Blue', 'Red'],
}
train = pd.DataFrame(data)
# データ
# category
# 0 Red
# 1 Blue
# 2 Green
# 3 Blue
# 4 Red
# ワンホットエンコーディング (One-Hot Encoding)
one_hot_encoded = pd.get_dummies(train['category'], prefix='category')
print("\n" + "/"*10 + "One-Hot Encoding" + "/"*20)
print(one_hot_encoded.astype(int))
# 出力
# //////////One-Hot Encoding////////////////////
# category_Blue category_Green category_Red
# 0 0 0 1
# 1 1 0 0
# 2 0 1 0
# 3 1 0 0
# 4 0 0 1
これにより、red=[0,0,1],bule=[1,0,0],green=[0,1,0]となり、データを機械が認識できるようになります。
エンコーディングには様々な種類があります。以下に各手法をまとめてあるので確認してみて下さい。
5.4 特徴量の追加/特徴エンジニアリング
新しい特徴量を生成または選択して、データセットを拡張します。
・例:異なる列を足すことで新しい列(情報)を作る
# 新しい特徴量column_newを生成
train['column_new'] = train['column1'] + train['column2']
より複雑で多岐にわたる手法を利用することで、モデルが利用できる情報を増やすことが特徴量エンジニアリングの目的です。しかし、特徴量を増やしすぎても計算コストが増加したり、適切な情報でない場合精度が低下する場合もあります。
適切な特徴量の追加はデータセットや課題に応じて大きく変化するため、ここでの具体的な手法の紹介は割愛することにします。
5.5 正規化(標準化)
データのスケールを揃えるため、正規化(標準化)を行います。
正規化: データを特定の範囲(例えば0から1)に収める
標準化: データの平均を0、標準偏差を1に変換する
・比較(正規化が緑、標準化がオレンジ)
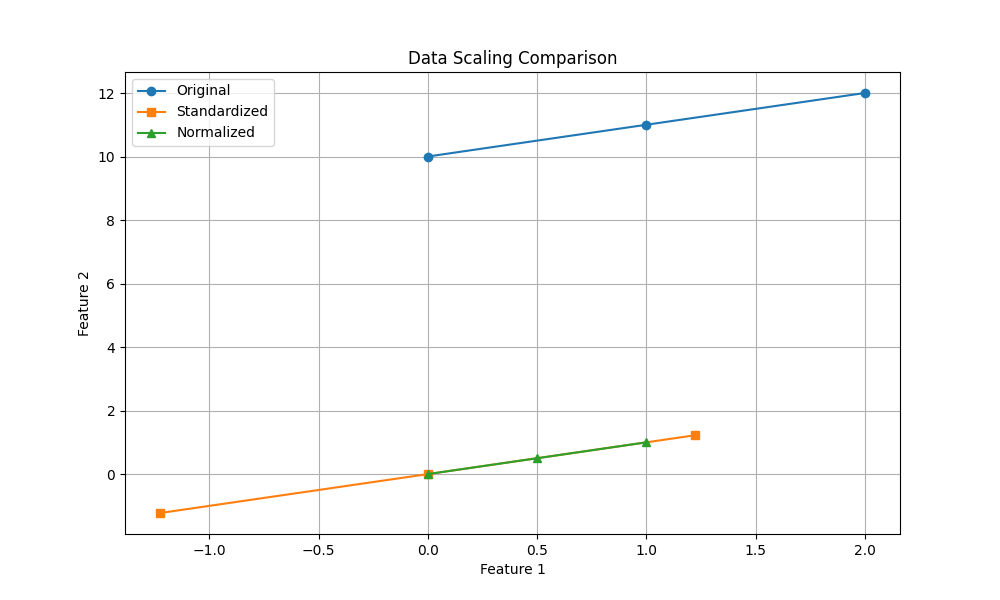
正規化(標準化)の目的は、大きすぎるデータの影響を低減し、モデルが特徴量を公平に評価できるようにすることです。これにより過学習のリスクも減少します。
5.6 次元削減
(必要に応じて)特徴量の数を減らすために、PCA、LDAなどの次元削減手法を適用します。
5.6.1 PCA(主成分分析)
PCAはデータの分散が最大となる方向を見つけ出し、その方向に沿ってデータを投影することにより、次元削減(特徴抽出)を行います。これは教師なし学習に分類されます。
分散は情報の多様性を表し、分散が大きいほど情報が多く存在することを示します。
以下のようなイメージで、それぞれの軸からの距離を新しいデータとします。
引用:AIsmiley
PCAの適用例
・Before

・After
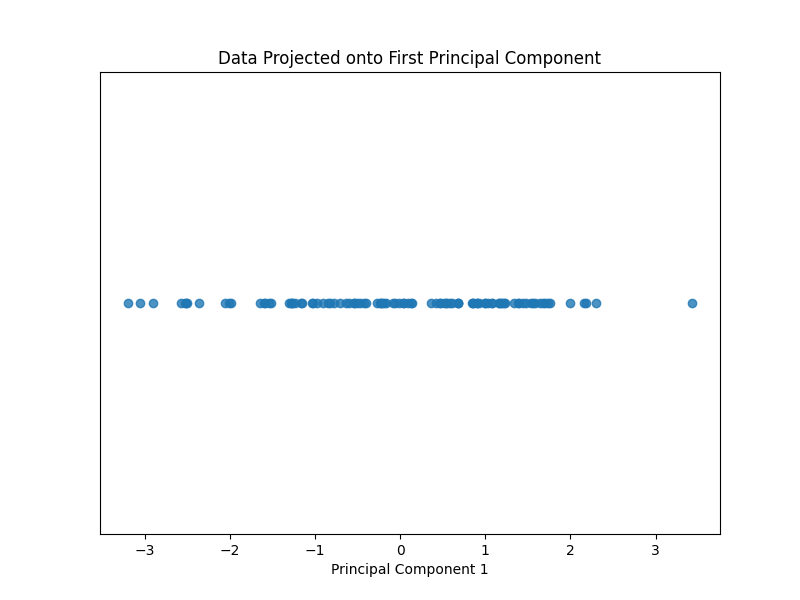
ここではデータを主成分に変換し、第一主成分(最もよくデータを表す成分)をプロットしています。これは、元データの右上を指す矢印と直交する線を軸として、この軸からの距離を表しています。
変換後の画像は元データの第一主成分を表しますが、このデータが具体的に何を示すのかは分かりません。この画像は、できるだけ情報を失わないように次元を落とした結果です。
5.6.2 LDA(線型判別分析)
LDAはクラス間の分離が最大になる方向を見つけ出し、その方向に沿ってデータを投影することにより、次元削減(特徴抽出)を行います。これは教師あり学習に分類されます。
LDAの適用例
・Before
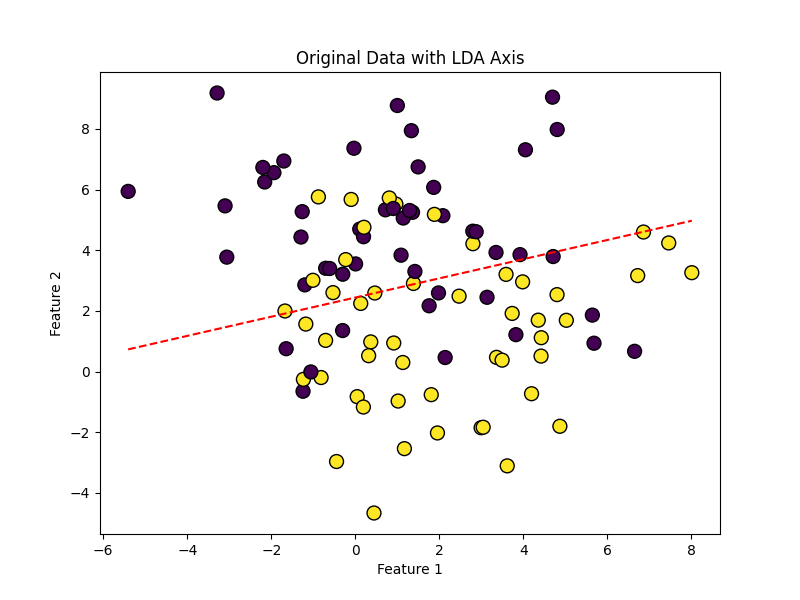
・After

この画像はデータの軸からの距離をプロットしています。この軸はデータ最もよく分離できる線分です。PCAではできるだけ情報を落とさないように次元を削減しましたが、LDAでは複数のクラスを最も分離できる線を軸とします。
5.6.3 次元削減による影響
上記の次元削減により、元データを「より解釈しやすい低次元に落としてからモデルに学習させる」ことができます。
例えば、LDA変換後のデータを利用すれば、人間もある程度新しいデータがどちらに属するか決めやすくなるのではないでしょうか。
具体的には、次にような効果があります。
- 処理速度
・計算効率が向上、複数のモデルを短期間で学習できる
・メモリ効率が向上、大規模データを扱える - 精度
・過学習を低減し、一般化能力が向上
・不要な特徴量やノイズを減らすことで、精度が向上
・しかし必要な特徴量が削除されてしまうと、精度が低下
次元削減は、特に高次元のデータセットや大規模データセットに対して効果を発揮します。
5.7 不均衡データの処理
必要に応じて、不均衡データの処理を行います。
不均衡データとは、以下のような一部のクラスのデータが他のデータに比べて極端に多い、または少ないデータのことをいいます。
・不均衡データ
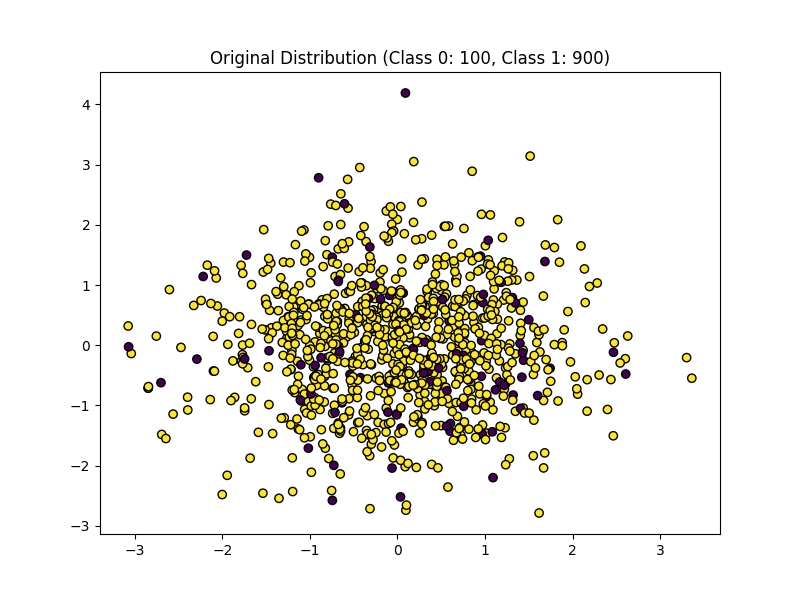
データセットが不均衡の場合、次のような理由でモデル性能が悪化します
- 学習の偏り
少数データのパターンを学習しきれず、これらに対する予測精度が低下します - 評価の誤謬
あるクラスが90%を占める場合、そのクラスを常に予測すると90%の精度を達成できます - 少数データに対する過学習
少数データに過剰適合し、少数データのノイズまで学習してしまうことがあります
不均衡データへの対処はいくつかありますが、ここではオーバーサンプリングまたはアンダーサンプリングを紹介します。
5.7.1 オーバーサンプリング
オーバーサンプリングは、データの数が揃うようにデータを追加する手法です。
・オーバーサンプリング(左:元データ, 右:オーバーサンプリング後のデータ)
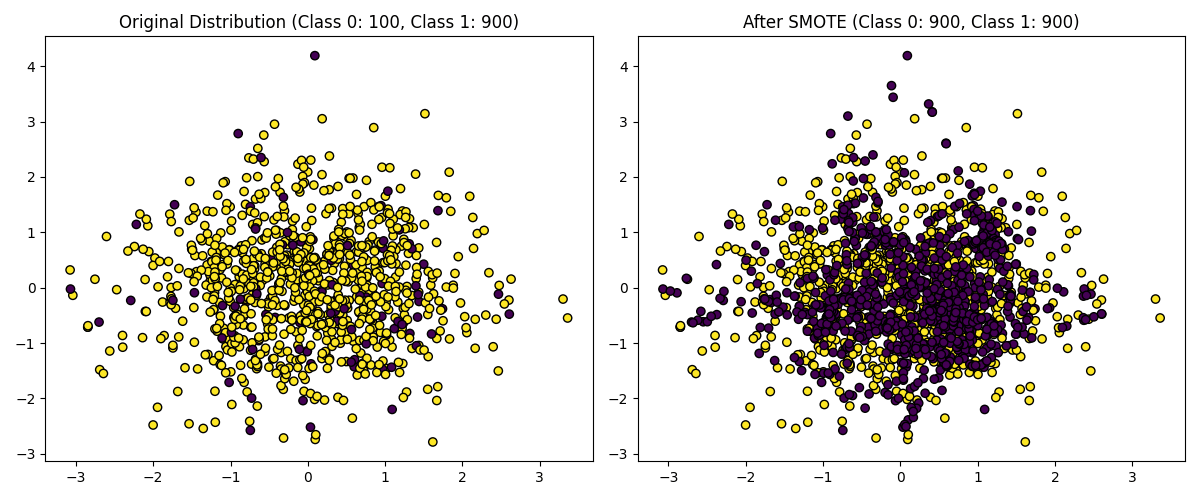
右の画像を見ると、データの数が等しくなっていることが分かります。
オーバーサンプリングには有名なSMOTEという手法があります。上のデータもSMOTEによりデータを追加しています。
- SMOTEの操作
- 少数データからランダムで一つ選ぶ(データa)
- データaの近くの少数データをk個選ぶ(k個のデータb)
- データaとデータbの間の線分上にランダムな点を選んで新しいデータcとします。
※オーバーサンプリングはデータの分布を変えるため、処理後に正規化を行うなど、注意して行う必要があります。
SMOTEは非常に簡単かつ有用であり、派生手法も数多く考案されています。
5.7.2 アンダーサンプリング
アンダーサンプリングは、データの数が揃うようにデータを削除する手法です。
こちらは非常に単純で、多数クラスのデータを少数クラスのデータ数になるまで削除します。具体的にはランダムな削除や、各クラスから代表値を選択して残すなどの手法があります。
・アンダーアンプリング(左:元データ, 右:アンダーサンプリング後のデータ)
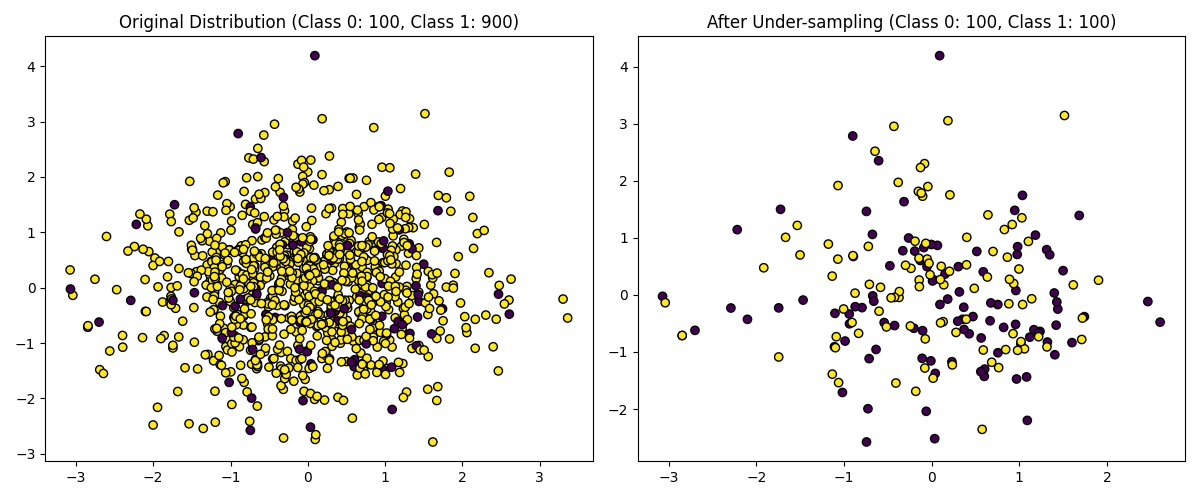
ここではランダムに多数クラスのデータを削除しています。右の画像はデータの数が等しくなっています。
5.8 バッチ正規化
ニューラルネットワークを使用する場合、学習プロセスを安定させ高速化するためにバッチ正規化を適用します。
バッチ正規化は、「入力データの分布が学習時と推論時で異なると、モデルの性能が悪化する」という現象を解決するために考案されました。
具体的には、モデルの各層の入力を毎回正規化することで、入力分布の一様化を図っています
・バッチ正規化の例
import tensorflow as tf
from tensorflow.keras.layers import Dense, BatchNormalization, Activation
from tensorflow.keras.models import Sequential
# モデルの定義
model = Sequential()
# 入力層
model.add(Dense(64, input_shape=(32,)))
model.add(BatchNormalization()) # 正規化
model.add(Activation('relu'))
# 隠れ層1
model.add(Dense(64))
model.add(BatchNormalization()) # 正規化
model.add(Activation('relu'))
# 隠れ層2
model.add(Dense(64))
model.add(BatchNormalization()) # 正規化
model.add(Activation('relu'))
# 出力層
model.add(Dense(1))
# モデルのコンパイル
model.compile(optimizer='adam', loss='mean_squared_error')
バッチ正規化は精度を向上させるための非常に強力な手法(dropoutが必要無いと言われる程)であり、また層が深くなるほどにその効力を発揮します。
5.9 データ拡張
画像や音声データなどに対して、データ拡張を行い、モデルの汎化能力を高めます。
より多くのデータを用意することで、モデルが多くの特徴を学習できるようになります。しかし、クラスとして不適切なデータを生成してしまうとモデルの精度が悪化するため、注意が必要です。
データ拡張には、画像を回転、拡大、縮小、平行移動、反転させるなど、多くの方法があります。
・データ拡張の例
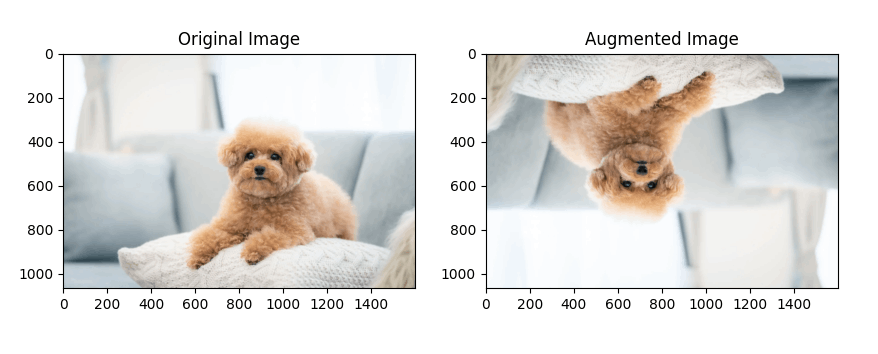
コード
import albumentations as A
import cv2
import matplotlib.pyplot as plt
# 拡張を定義
transform = A.Compose([
A.HorizontalFlip(p=0.5), # 50%の確率で水平方向に反転
A.RandomBrightnessContrast(p=0.2), # 明るさとコントラストをランダムに変更
A.Rotate(limit=30), # 最大30度でランダムに回転
A.VerticalFlip(p=0.5), # 50%の確率で垂直方向に反転
])
# 画像を読み込む
image_path = '/kaggle/input/a-simple-dog/dog.png' # 実際の画像パスに置き換えてください
image = cv2.imread(image_path)
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB) # OpenCVはBGR形式で画像を読み込むのでRGBに変換
# 拡張を適用
augmented_image = transform(image=image)['image']
# 画像を表示
plt.figure(figsize=(10, 10))
plt.subplot(1, 2, 1)
plt.title('Original Image')
plt.imshow(image)
plt.subplot(1, 2, 2)
plt.title('Augmented Image')
plt.imshow(augmented_image)
plt.show()
データ拡張の効力は、データセットによって異なります。そのため、実際に試してみるまでその有効性を完全には知ることができない場合が多いです。
一般的には、試してみて精度が向上したものを利用する、というアプローチが多いと思います。
5.10 時系列データの処理
時系列データに対して、トレンド除去、季節性調整、差分化などを行います。
ここでは簡単な紹介のみ行います。
5.10.1 トレンド除去

トレンド除去では長期的な変動を除去し、短期的な変化を捉えます。
5.10.2 季節性調整
季節性調整では、一定期間(例えば、1年、1月、1週間)ごとに発生する規則的な変動を取り除き、長期的な変動を捉えます。
5.10.3 差分化
差分化は、連続するデータに対して一定時間を開けて差分を取る手法です。
以下におおまかな差分か手法を示します。
・一次差分: 連続する各観測値間の差を計算します。これは時系列の隣接する2つの値の差を取ることを表します。数学的には、D_t = Y_t - Y_(t-1) となります。
・二次差分: 一次差分の差分をとります。物理の加速度のようなイメージで分析できます。
・季節性差分: 季節の長さに等しい期間のデータ点間で差分を取ります。例えば月次データの場合、データ点間は12ヶ月です。
コード
可視化コード
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import signal
# 仮想的な時系列データの生成
np.random.seed(0)
time = np.arange(0, 100, 1)
trend = time * 2.5
seasonality = 10 + np.sin(time) * 10
data = trend + seasonality + np.random.normal(size=time.size)
# トレンド除去
detrended = signal.detrend(data)
# 可視化
plt.figure(figsize=(10, 6))
plt.plot(time, data, label='Original Data')
plt.plot(time, detrended, label='Detrended Data')
plt.legend()
plt.savefig('/Users/yuto/Downloads/Programing/zenn/image/MLmodel_introduction/Chapter5/Detrended_Data.png')
plt.show()
from statsmodels.tsa.seasonal import seasonal_decompose
# 季節性調整
result = seasonal_decompose(data, model='additive', period=10)
seasonally_adjusted = data - result.seasonal
# 可視化
plt.figure(figsize=(10, 6))
plt.plot(time, data, label='Original Data')
plt.plot(time, seasonally_adjusted, label='Seasonally Adjusted Data')
plt.legend()
plt.savefig('/Users/yuto/Downloads/Programing/zenn/image/MLmodel_introduction/Chapter5/Seasonally_Adjusted_Data.png')
plt.show()
# 差分化
differenced = np.diff(data, n=1)
# 可視化
plt.figure(figsize=(10, 6))
plt.plot(time[1:], differenced, label='Differenced Data')
plt.legend()
plt.savefig('/Users/yuto/Downloads/Programing/zenn/image/MLmodel_introduction/Chapter5/Differenced_Data.png')
plt.show()
Step5まとめ
今回は、データの前処理について解説しました。
次回Step6は、実際に生のデータへの前処理を実践する予定です。
最後まで読んでいただきありがとうございました。
参考
(1) 主成分分析(PCA)とは?機械学習での活用例や固有値などについて解説
付録
正規化/標準化比較用コード
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler, MinMaxScaler
# 元のデータ
data = np.array([[0, 10], [1, 11], [2, 12]])
# 標準化
scaler = StandardScaler()
standardized_data = scaler.fit_transform(data)
# 正規化
minmax_scaler = MinMaxScaler()
normalized_data = minmax_scaler.fit_transform(data)
# プロットの設定
plt.figure(figsize=(10, 6))
# 元のデータのプロット
plt.plot(data[:, 0], data[:, 1], 'o-', label='Original')
# 標準化されたデータのプロット
plt.plot(standardized_data[:, 0], standardized_data[:, 1], 's-', label='Standardized')
# 正規化されたデータのプロット
plt.plot(normalized_data[:, 0], normalized_data[:, 1], '^-', label='Normalized')
plt.title('Data Scaling Comparison')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.grid(True)
plt.show()
PCA(主成分分析)の可視化コード
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
np.random.seed(0)
mean = [0, 0]
cov = [[1, 0.8], [0.8, 1]]
X = np.random.multivariate_normal(mean, cov, 100)
# PCAの実行
n_components = 2
pca = PCA(n_components=n_components)
pca.fit(X)
# 抽出主成分数
components = pca.components_
explained_variance_ratio = pca.explained_variance_ratio_
# データを主成分に変換
X_pca = pca.transform(X)
# プロット
plt.figure(figsize=(6, 6))
plt.scatter(X[:, 0], X[:, 1])
# 変換前のデータをプロット
for i, component in enumerate(components):
# 主成分の軸をプロット
plt.arrow(mean[0], mean[1], component[0]*explained_variance_ratio[i], component[1]*explained_variance_ratio[i], head_width=0.1, head_length=0.1, fc='red', ec='red')
# 寄与率のテキストを追加
plt.text(mean[0] + component[0]*explained_variance_ratio[i],
mean[1] + component[1]*explained_variance_ratio[i] - 0.3,
f"{explained_variance_ratio[i]:.2f}",
color='red')
plt.title("Original Data with PCA Axes")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.axis('equal')
plt.show()
# 主成分に変換後のデータをプロット
plt.figure(figsize=(8, 6))
plt.scatter(X_pca[:, 0], np.zeros_like(X_pca[:, 0]), alpha=0.8) # 第一主成分を可視化
# plt.scatter(X_pca[:, 0], X_pca[:, 1]) # 第二主成分も併せて可視化
plt.title("Data Projected onto First Principal Component")
plt.xlabel("Principal Component 1")
plt.yticks([])
plt.show()
LDA(線型判別分析)の可視化コード
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
# データセットの生成
X, y = make_blobs(n_samples=100, centers=2, n_features=2, cluster_std=2.5, random_state=0)
# LDAのインスタンスを作成し、データにフィットさせる
lda = LDA(n_components=1)
lda.fit(X, y)
# 分離軸の方向を取得
coef = lda.coef_
intercept = lda.intercept_
# 分離軸をプロットに追加
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', edgecolor='k', s=100)
# 分離線を計算してプロット
x_values = np.linspace(X[:, 0].min(), X[:, 0].max(), 100)
y_values = -(x_values * coef[0, 0] + intercept) / coef[0, 1]
plt.plot(x_values, y_values, 'r--')
# データの描画
plt.title("Original Data with LDA Axis")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()
# LDAの実行
# LDAのインスタンスを作成し、データにフィットさせる
lda = LDA(n_components=1)
X_lda = lda.fit_transform(X, y)
# LDA変換後のデータをプロット
plt.figure(figsize=(8, 6))
plt.scatter(X_lda, np.zeros_like(X_lda), c=y, cmap='viridis', edgecolor='k', s=100)
plt.title("LDA Transformed Data")
plt.xlabel("LDA Component 1")
plt.yticks([])
plt.show()
オーバー/アンダーサンプリング可視化コード
import matplotlib.pyplot as plt
from collections import Counter
from sklearn.datasets import make_classification
from imblearn.over_sampling import SMOTE
from imblearn.under_sampling import RandomUnderSampler
# 仮想的な不均衡データセットの生成
X, y = make_classification(n_classes=2, class_sep=2, weights=[0.1, 0.9], n_informative=3, n_redundant=1, flip_y=0, n_features=20, n_clusters_per_class=1, n_samples=1000, random_state=10)
# オリジナルデータのプロット
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', edgecolor='k', label="Class")
plt.title(f'Original Distribution (Class 0: {Counter(y)[0]}, Class 1: {Counter(y)[1]})')
# SMOTEを用いたオーバーサンプリング
smote = SMOTE(random_state=42)
X_res, y_res = smote.fit_resample(X, y)
plt.subplot(1, 2, 2)
plt.scatter(X_res[:, 0], X_res[:, 1], c=y_res, cmap='viridis', edgecolor='k', label="Class")
plt.title(f'After SMOTE (Class 0: {Counter(y_res)[0]}, Class 1: {Counter(y_res)[1]})')
plt.tight_layout()
plt.show()
# オリジナルデータのプロット
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', edgecolor='k', label="Class")
plt.title(f'Original Distribution (Class 0: {Counter(y)[0]}, Class 1: {Counter(y)[1]})')
# ランダムアンダーサンプリング
rus = RandomUnderSampler(random_state=42)
X_res_under, y_res_under = rus.fit_resample(X, y)
plt.subplot(1, 2, 2)
plt.scatter(X_res_under[:, 0], X_res_under[:, 1], c=y_res_under, cmap='viridis', edgecolor='k', label="Class")
plt.title(f'After Under-sampling (Class 0: {Counter(y_res_under)[0]}, Class 1: {Counter(y_res_under)[1]})')
plt.tight_layout()
plt.show()
Discussion