【Wave Analytics Method】What is CWT/Scarogram

1. CWT/Scarogram

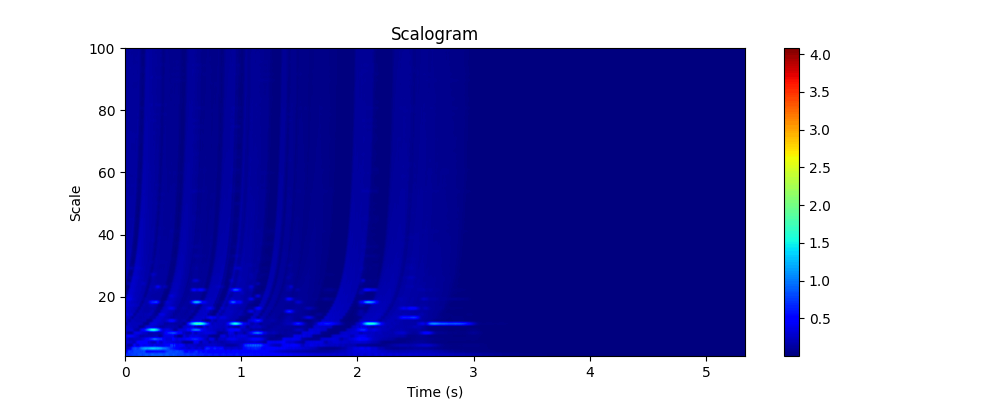
Scarogram is a 2-dimentional image created by applying CWT(Continous Wavelet Transform) to 1-dimentional signal.

・Scarogram

2. Wavelet Transform

2.1 Wavelet

What is wavelet? It is a function that take time as an argument. Generally, be represented as$\Psi(t)$.

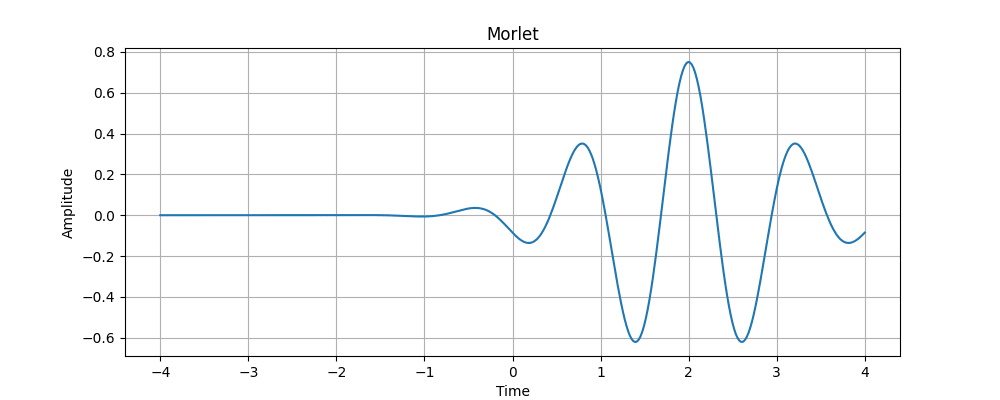
Wavelet has a variety of types. Morlet is a famous one.
・Wavelet

To be a proper wavelet, function has to satisfy 2 main constraints.

1. Zero mean:$\int^{+ \infty}_{- \infty} \Psi (t)dt = 0$
2. Finite energy:$\int^{+ \infty}_{- \infty} |\Psi(t)|^2 dt < \infty$
   Example, sin function not satisfy condition 2, because it has infinite energy.
   You can think of those constraints as indicating a converging fanction with zero mean.

2.2 Adjust Wavelet

In below, choice morlet as wavelet.

Morlet

・Morlet

When we adjust $t$ by $b$, the morlet changes shape accordingly.
・$(t - b)$
b = 2

・$(\dfrac{t}{a})$
a = 0.5

Thorefore, we can create various morlet by control $b$ and $a$ in $\Psi(\dfrac{t-b}{a})$.
b = -2, a = 0.25

2.3 Wavelet Transform

Wavelet Transform create image that one axis represent frequency, and one another represent time from signal.

・Wavelet Transform
$y(t) \rightarrow T(t,f)$
The right arrow represent Wavelet Transform, what is going on there? Let's check in below.

・Calculation 1
$y(t) \cdot \Psi_{a,b}(t)$
$y$: Be analyzed signal

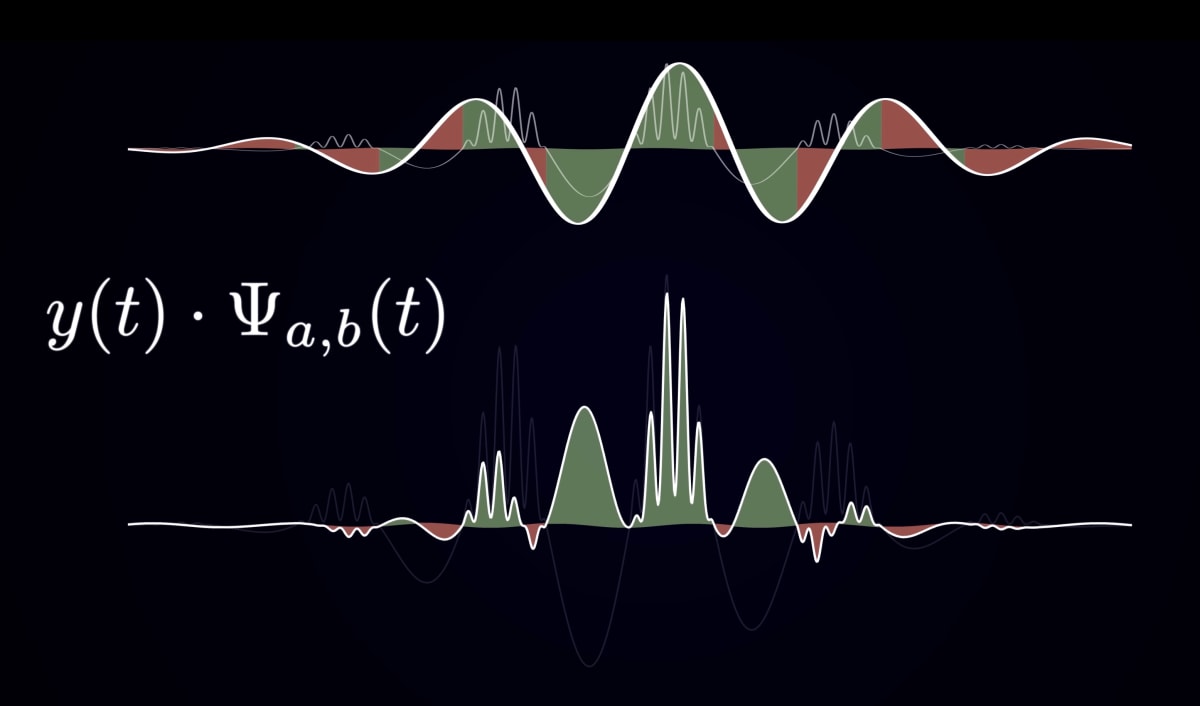
This calculation creates a new wave(ex. above jagged wave) that shows how similar each function is. At every point, if the values of each function($y$, $Psi$) are close, amplitude of new wave is higher.

Created wave represent similarity of two waves y(t) and Ψ.

・Calculation 2
$T(a,b) = \int^{+\infty}_{-\infty} y(t) \cdot \Psi_{a,b}(t) dt$

This formula calculates the total area of overlap between the Morlet and the original formula, assuming that if the overlapped parts have the same sign, it is a plus, and if they have different signs, it is a minus.
In other words, it shows the degree of overlap between morlet and the original signal.

2.4 Imaginary part

Wavelet has a imaginary part. And as same with real part, $T_i(a,b)$ is calculated by imaginary part.

It provide more generality to Wave Transform(WT).

2.5 Result of Transform

The $T(a, b)$ in caluclate 2 is the result of WT.
$T$ is a function representing the degree of matching between the Morlet wavelet and the original function.

Parameter $b$

If you change parameter b, T shows similarity between two functions in the according time. It makes a one-dimensional wave that shows where there is a similar wave to wavelte with frequency of $T$ (based on parameter $a$).

Parameter $a$

When you repeat the same process in changing parameter a, you can obtain various waves that show where each wave has the same frequency corresponding to parameter a.

Power

In this time, we got $T$ for the entire time and frequency axis when $a$ and $b$ are moved.

After obtaining $T(a,b)$ and $T_i(a,b)$(imaginary part of $T$) in this way, obtain the square of their absolute value as power.

Power $= \sqrt{T(a,b)^2 + T_i(a,b)^2}^2 = T(a,b)^2 + T_i(a,b)^2$

Scarogram

When you get this far, all you have to do is color map the frequency components of each power and arrange them in time. And you'll get Scarogram.
It's same operation when you create spectrogram.

It shows at what time in the original waveform a waveform with the same frequency component (varied by $a$) as the wavelet exists.

summary

This time, I explained about CWT/Scarogram.
Thank you for reading.

Reference

(1) Wavelets: a mathematical microscope, Artem Kirsanov