ゴリラで学ぶ交差エントロピー誤差

今回は交差エントロピー誤差について解説します。

交差エントロピー誤差:

$E = -\sum\limits_k(t_k*log(y_k))$

Σがあると分かりづらいので中の要素だけを見てみると、$t*log(y)$となります。

ここで$t$は正解データのインデックスです。例えば動物画像の分類で[キリン、ゾウ、ゴリラ]の可能性があるとして、ゴリラが正解の時は$t = [0,0,1]$ となります。
$y$は予測値であり、0~1の範囲をとり、合計は1になります。例えば$y = [0.1,0.1,0.8]$の場合、ゴリラである確率が最も高いことになります。

これを踏まえて $E = t * log(y)$を計算すると、
キリンとゾウについてはt=0のためE=0
ゴリラは$E = 1*log(0.8) = -0.096910013$となります。

ちなみにlogのグラフは以下のようになっており、yの値(x軸)が0に近づくほど、大きくマイナスになっていくことが分かります。

さて、元々の交差エントロピー誤差は$E = -\sum\limits_k(t_k*log(y_k))$でしたので、これを求めるために、ゾウ、キリン、ゴリラそれぞれの$E$３つを足してマイナスをかけると、$E = 0.096910013$となります。

これはゴリラ要素の$E$の値と同じであり、ゴリラの予測値のみが$E$に影響を与えていることが分かります。つまり、交差エントロピー誤差とは、「正解データに対する予測値の大きさ$y(0~1)$」によってのみ決まります。
また上の図から分かるように、yが0に近づくほど大きくなり、予測値(0~1)が1に近づく(ゴリラである確率が高い)ほどEは小さくなります。

まとめ

交差エントロピー誤差は、正解ラベルに対する予測値のみで決まり、その値はlog(y)の負の数となる。つまり予測値の変化に対して、以下のグラフのような値になります。(最高値は1)
・交差エントロピー誤差

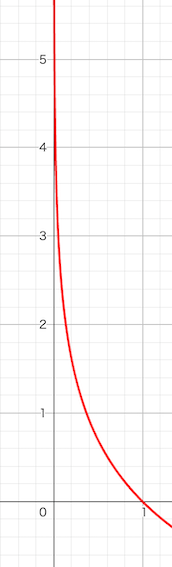
この特性から、「予測値が正解に近いほど、値が小さくなっていく」という損失関数としての役割を果たしています。

正解データが1に近いほど交差エントロピー誤差は小さくなるので、間接的に他の予測データが0に近づくように学習されるのです。

説明は以上です。間違いがありましたら教えて下さい！誰かの役に立っていれば幸いです！