誤差逆伝播法を完全に理解したので、忘れないうちに書き留めておきます。
- ニューラルネットワークについてなんとなく理解しているよって人向けです!
誤差逆伝播法とは?
誤差逆伝播法はニューラルネットワークのパラメータ更新を自動で行う手法です。
詳しくは述べませんが、次の式によってニューラルネットワークのパラメータを更新(いわゆる学習と呼ばれるプロセス)することができます。
w' = w - η\dfrac{∂L}{∂w}: パラメータwの更新式
w: パラメータ
L: 損失関数
η: 学習率
学習率ηは任意の値なので置いておいて、パラメータwをパラメータw'へ更新するためには損失関数Lに対するwの偏微分\dfrac{∂L}{∂w}を求める必要があります。
これを求めるための手法が誤差逆伝播法です。
どのように求めるか
\dfrac{∂L}{∂w}を単純に求めることができれば楽なのですが、ニューラルネットワークは網目のような形状をしており、一つのパラメータwが広範囲に広がって損失関数Lに影響を与えています。
そのため解析的に正攻法で解くことはほぼ不可能です。
そこで、損失関数Lから逆算して求める方法が考案されました。
具体的に考えていきましょう。次のようなニューラルネットワークを考えます。
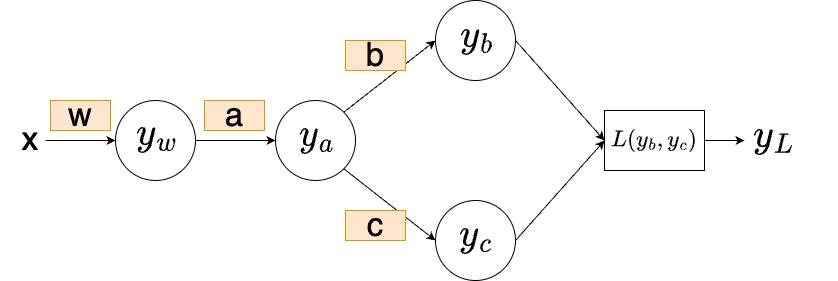
xが入力、w,a,b,cは全てパラメータ(重み)で、yが出力です。y_Lが損失関数Lの出力です。
このとき、L=y_L^{*1}に対するwの偏微分\dfrac{∂L}{∂w}はどのように計算できるでしょうか?
ここで、連鎖律という考え方を使用します。
- 連鎖律
重みを更新する際、連鎖律と呼ばれる微分の手法を使用します。
これはE(y(x))の時、
Eに対するxの偏微分\dfrac{∂E}{∂x}が
\dfrac{∂E}{∂x}=\dfrac{∂E}{∂y}\dfrac{∂y}{∂x}と変形できる性質のことです。
これを多変数に展開すると、
E(u,v)かつu(x,y),v(x,y)の時、Eに対するxの偏微分\dfrac{∂E}{∂x}が
\dfrac{∂E}{∂x}=\dfrac{∂E}{∂u}\dfrac{∂u}{∂x}+\dfrac{∂E}{∂v}\dfrac{∂v}{∂x}
となります。これはつまり多変数関数で連鎖律を使用する際には、変数xが影響を及ぼしている全ての関数の連鎖律の総和が必要であるということです。これにより特定の変数がEへ与える影響を考えることができます。
では再度図を示します。

上の図でLは出力y_w,y_a,y_b,y_cの関数であり、y_wはwの関数であると考えられるので、連鎖率より
\dfrac{∂L}{∂w} = \dfrac{∂L}{∂y_b}\dfrac{∂y_b}{∂y_a}\dfrac{∂y_a}{∂y_w}\dfrac{∂y_w}{∂w}+\dfrac{∂L}{∂y_c}\dfrac{∂y_c}{∂y_a}\dfrac{∂y_a}{∂y_w}\dfrac{∂y_w}{∂w}
と計算できます^{*2}。そして、これを一度に計算するのではなく、\dfrac{∂L}{∂y_b}を計算し、それを利用して\dfrac{∂L}{∂y_b}×\dfrac{∂y_b}{∂y_a}を計算し、\dfrac{∂L}{∂y_b}×\dfrac{∂y_b}{∂y_a}×\dfrac{∂y_a}{∂y_w}を計算し…というように、最終的な関数Lから遡って計算を行います。(機械学習のフレームワークでは、自動で遡って計算する機能が組み込まれています)
1つ1つの計算は単純なので、プログラムで自動的に全て求めることができるのです。
例えば\dfrac{∂y_b}{∂y_a}などは、y_b=b*y_aなので、\dfrac{∂y_b}{∂y_a} = bとなります。今回は単純なかけ算なので、かけた値が「出力に影響を与えた大きさ」として逆伝播していきます。
そして、求めた\dfrac{∂L}{∂w}を利用して、
w' = w - η\dfrac{∂L}{∂w}の式によってパラメータwを更新し、更新後のパラメータw'で上記の計算を行い、さらにw''を求めて、、、というふうにパラメータを更新します。
この動作によって、損失関数Lが少なくなるようにパラメータwが変化していきます。
損失関数Lがある程度まで小さくなったら、パラメータw^nを固定してニューラルネットワークの学習は終了です。
そのパラメータを固定したニューラルネットワークに、新しい入力を入れることで回帰などが行えます。
さいごに
今回の計算は連鎖律によって行われ、ニューラルネット上でパラメータwが関わるすべての連鎖律の総和を取る必要がありました。
パラメータwが与えたすべての影響について、連鎖律による逆伝播の加算という形で計算することで、「広範囲に広がった影響」を「元のパラメータ」の場所まで集めることができるのです。
このように、簡単な計算で\dfrac{∂L}{∂w}を求めていく手法が誤差逆伝播法でした。
また今回はかけ算のみでしたが、上で示したようにかけ算のみだと値がそのまま戻るだけであり、表現力に乏しいモデルになってしまいます。これを改善するために、一般的なニューラルネットワークでは活性化関数と呼ばれる非線形の関数fを出力yに適用して、f(y)を出力として計算していきます。
これにより、柔軟な表現が可能なニューラルネットワークが出来上がるのです。
補遺
^{*1} L=y_Lとできるのは、関数Lを実際に計算することでy_Lが求まるためです。Lについて重みwの偏微分を求めることは、wを変化させることでどれだけLの出力y_Lが変化するかを求める事に等しくなります。
^{*2} \dfrac{∂L}{∂w}なども同様に、\dfrac{∂L}{∂w} = \dfrac{∂L}{∂y_b}\dfrac{∂y_b}{∂b}として最終項の分母を{∂b}に変更することで求められます。(パラメータbからは分岐していないので式は単純になります)
※誤差逆伝播は、特定の関数(損失関数)に対して実行されます。ニューラルネットの出力結果ではなく、出力結果と正解データの差異を計算する関数に対して実行され、差異を減らす方向にニューラルネットワークのパラメータを更新します。


Discussion