【ML Method】k-means and k-NN

This time, I'll explain both K-Means and K-Nearest Neighbors (k-NN), followed by some example code for each.

0. k-means and k-NN are similar?

K-Means and k-NN may seem similar algorithms from their names, but they are based on completely different goals and concepts.

1. Different goals
   ・k-Means:
   A clustering algorithm that divides unlabeled data into groups (clusters). It is used to discover structures in data and group similar data together. It is a type of unsupervised learning.
   ・k-NN:
   A supervised learning algorithm used for classification and regression. Its goal is to classify new data based on the labels of nearby data points in an already labeled dataset.
2. Different ways of handling data
   ・k-Means:
   To divide data into K clusters, each data point is assigned based on its distance to a centroid. The centroid is then recalculated to iteratively improve the clusters.
   ・k-NN:
   For each new data point, K nearest data points in the training dataset are chosen and predictions are made based on their labels. Distance is used to measure the similarity between data.

These are different concepts, but I will explain each of them here.

1. K-Means Clustering

K-Means is an unsupervised learning algorithm used for clustering. It tries to group data into K clusters, where each data point belongs to the cluster with the nearest mean. The algorithm iteratively adjusts the positions of the cluster centers until convergence.

1.1 Steps

1. Initialize K centroids (randomly or using other methods).
2. Assign points to the nearest centroid (forming clusters).
3. Update centroids by calculating the mean of the points in each cluster.
4. Repeat steps 2 and 3 until convergence (no change in cluster assignments).

1.2 Code Example

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs

def kmeans(X, k, max_iters=100):
    # Randomly initialize centroids
    centroids = X[np.random.choice(X.shape[0], k, replace=False)]
    
    for _ in range(max_iters):
        # Assign points to nearest centroid
        labels = np.argmin(np.linalg.norm(X[:, np.newaxis] - centroids, axis=2), axis=1)
        
        # Update centroids
        new_centroids = np.array([X[labels == i].mean(axis=0) for i in range(k)])
        
        # Check for convergence
        if np.all(centroids == new_centroids):
            break
        
        centroids = new_centroids
    
    return labels, centroids

# Generate sample data
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)

# Apply k-means
k = 4
labels, centroids = kmeans(X, k)

# Plot results
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')
plt.scatter(centroids[:, 0], centroids[:, 1], c='red', marker='x', s=200, linewidths=3)
plt.title('K-means Clustering')
plt.show()

1.3 Results

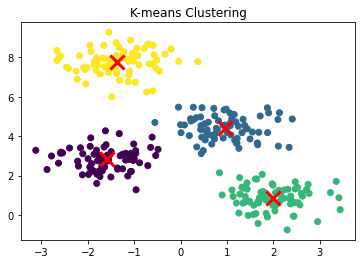
1.4 supplement

The k-means method has the problem that its accuracy varies depending on the initial random cluster allocation. There is also a method called k-means++ that attempts to overcome this problem.

2. K-Nearest Neighbors (k-NN)

K-Nearest Neighbors is a supervised learning algorithm used for classification and regression. In classification, it works by assigning a label to a new data point based on the labels of its K nearest neighbors.

2.1 Steps

1. Choose the number of neighbors K.
2. Calculate the distance between the new data point and all other points.
3. Select the K nearest neighbors (based on distance).
4. Vote for the most frequent class among the neighbors (classification) or average their values (regression).

2.2 Code Example

import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

def knn_classify(X_train, y_train, X_test, k):
    predictions = []
    
    for test_point in X_test:
        # Calculate distances
        distances = np.linalg.norm(X_train - test_point, axis=1)
        
        # Find k nearest neighbors
        k_indices = np.argsort(distances)[:k]
        k_nearest_labels = y_train[k_indices]
        
        # Make prediction (majority vote)
        prediction = np.bincount(k_nearest_labels).argmax()
        predictions.append(prediction)
    
    return np.array(predictions)

# Load iris dataset
iris = load_iris()
X, y = iris.data, iris.target

# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Apply k-NN
k = 3
y_pred = knn_classify(X_train, y_train, X_test, k)

# Calculate accuracy
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")

2.3 Results

Accuracy: 1.00

3. Differences

1. K-Means is for clustering (unsupervised), while k-NN is for classification or regression (supervised).
2. K-Means divides data into clusters, while k-NN uses proximity to labeled data points to classify new data.

4. Summary