🐰

Batch Normalization/バッチ正規化とは

2024/02/18に公開

機械学習

tech

今回はBatch Normalizarionについて解説します。
原論文(2015)

0. 概論

Batch Normalizationは主に勾配消失・爆発を防ぎ、学習を安定化、高速化させるための手法です。

従来手法
・活性化関数を変更する（ReLUなど）
・ネットワークの重みの初期値を事前学習する
・学習係数を下げる
・ネットワークの自由度を制約する（Dropoutなど）

Batch Normalizationはこれまでとは違い、ネットワークの学習プロセスを全体的に安定化させて学習速度を高めることに成功しました。

DCGAN(バッチ正規化を含むモデル)を試した開発者の発言

DCGANを使用した生成モデルを試した開発者の発言を引用します。

"一番効いてきているのがBatch NormalizationとAdamでした。これ入れないとそもそもノイズしか出てきません．個人的な印象だと，DCGANの一番の貢献はBNを入れたことだと思います。それ位違いがある。だとすれば、例えばDAEやVAE等の別のモデルでも，上手く行かなかったのは単なるBNの不在である可能性がある。"

1. 事前知識

1.1 内部の共変量シフト

共変量シフトとは、機械学習の分野ではモデルが訓練された環境（訓練データセット）と、実際に適用される環境（テストデータセット）の間で、入力データの分布が変化する現象のことを指します。

・例：訓練データと推論用データの分布に異なりがある状態

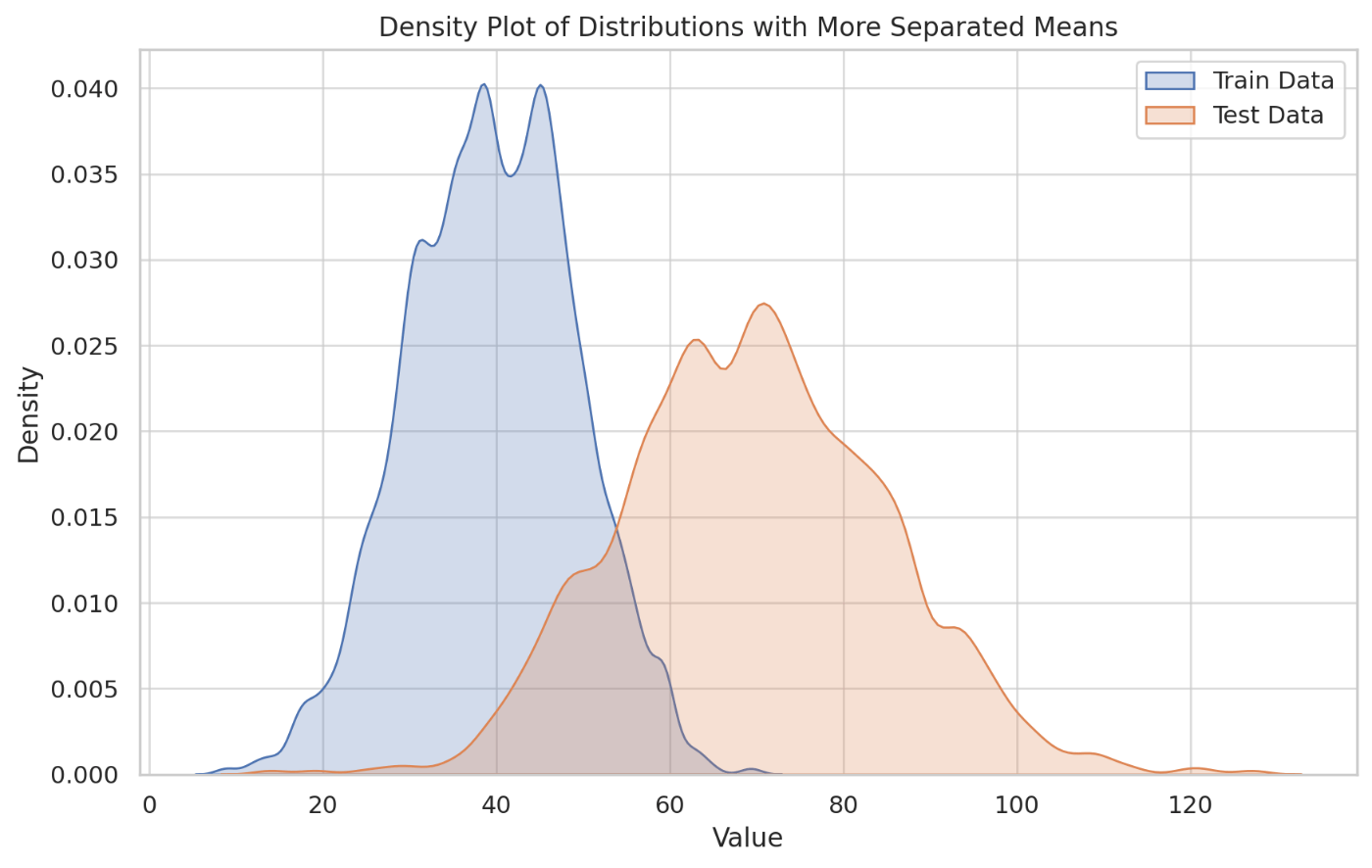
機械学習モデルは、訓練用入力データの分布をもとに学習を行うため、訓練用データの分布に対して最適化されます。
そのため、推論時の入力データ分布が訓練時と異なる場合、モデルの性能が落ちる可能性が高くなります。

特にディープラーニングにおいては、深いネットワークの隠れ層を通るにつれて、各層の入力データの分布が徐々に変化していく問題が発生します。これを「内部の共変量シフト（Internal Covariate Shift）」と呼びます。
ネットワークが深くなるほど、層を重ねるごとに、前の層の出力（次の層の入力）の分布が変わるため、学習が困難になります。つまり、ネットワークの初期層での微小な変更が、後続の層へと伝播し、全体の学習プロセスに影響を及ぼすのです。

これを解決するために、白色化と呼ばれる「データの各特徴量を平均0、分散1に変換し、また特徴量間の相関を除去する処理」を行うと、ニューラルネットワークの収束速度が速くなることが知られています。

これまでも、データの前処理において白色化のような正規化を行なってきました。
実際、データセットの分散が偏っている場合(正規化していない場合)、通常(一次情報のみ)の勾配法だと収束速度が遅くなります。これは、白色化が内部の共変量シフトを抑制する働きがあることを示しています。
しかしデータセットだけ白色化されていても、ネットワーク内部で分散が偏ります。

この問題を解決するために提案されているのがバッチ正規化（Batch Normalization）などのテクニックです。
バッチ正規化は、各層の入力を正規化することで、層間の入力分布の変化を安定させ、内部の共変量シフトを軽減します。これにより、学習プロセスが安定し、高速化されるとともに、ディープネットワークの性能が向上するとされています。

2. Batch Nomarlization

まず入力としてm個のデータからなるミニバッチ
$B = \{\textbf{x}_1 ... \textbf{x}_m\}$

と学習されるべきパラメータ( $\gamma$ が平均、 $\beta$ が標準偏差に対応)
$\gamma, \beta$

があるとします。初めにミニバッチ内での平均 $\mu_B$ と分散 $\delta^2_B$ を計算します。
$\mu_B= \dfrac{1}{m}\sum\limits_{i=1}^m \textbf{x}_i$
$\delta^2_B = \dfrac{1}{m}\sum\limits_{i=1}^m (\textbf{x}_i - \mu_B)^2$

これらの値を使い、ミニバッチの各要素 $\textbf{x}_i$ を平均を0、分散が1となるように(Zスコア変換)変換します。( $\hat{\textbf{x}}$ は $\textbf{x}$ の推定値を示す)
$\hat{\textbf{x}} = \dfrac{\textbf{x}_i - \mu}{\sqrt{\delta^2_B + \epsilon}}$
$\textbf{y}_i = \gamma \hat{x} + \beta$

この手続きで得られた $\{\textbf{y}_i ... \textbf{y}_m\}$ がBatch Normalizationの出力となります。

ここでの発想は、全データではなくバッチごとに正規化を行うというものです。

γ,βの必要性

$\gamma, \beta$ は、活性化関数への入力範囲によって、非線形変換ができなくなることを防ぎます。

例えばsigmoid関数を見ると、中心部分はほとんどy=ax+bのような線形の形になっていることが分かります。(ReLUも同様にx>0で線形変換を行います)
この関数への入力が平均0,標準偏差1では活性化関数の非線形を活かすことができません。

活性化関数の目的はモデルに非線形性を追加して、より高度な表現力を獲得することですので、
$\gamma, \beta$ を利用して入力の範囲をずらすことで、活性化関数の非線形な部分を活用できるように、このパラメータの学習が行われるのです。
例えば、 $\gamma=0, \beta=1$ に近ければ単純に正規化したものに近く、それ以外の場合はパラメータによるスケールやシフトによって必要な非線形性を得られるように学習していると言えます。

大まかには上記の計算がBatch Normalizationですが、推論時には $\gamma, \beta$ は最終学習時のまま固定し、分散や平均は推論時のデータ全体から計算されたものが、学習時のものに追加されます。

・推論時の平均と分散
平均: $\mu = E[\mu_{testB}] × (momentum -1) + \mu_{trainB} × momentum$
分散: $\delta^2 = E[\delta^2_{testB}] × (\dfrac{m}{m-1}) × (momentum -1) + \delta^2_{trainB} × momentum$
$E$ : 期待値
$m$ : サンプルサイズ(データポイントの数)
※ $(\dfrac{m}{m-1})$ はベッセルの補正と呼ばれ、標本分散が母集団分散を過小評価する傾向にあることを補正するために使用されます。

momentumの割合が大きい(0.9など)ほど、「推論時の全データから計算された平均 $E[\mu_{testB}]$ や分散 $E[\delta^2_{testB}]$ 」(バッチデータ毎の分散と平均の平均値)は正規化に使用されなくなります。

以下に実装コードを記載します。ここで詳細な動作を確認できます。

・実装

def batchnorm_forward(x, gamma, beta, bn_param):
    """
    Forward pass for batch normalization.
    During training the sample mean and (uncorrected) sample variance are
    computed from minibatch statistics and used to normalize the incoming data.
    During training we also keep an exponentially decaying running mean of the
    mean and variance of each feature, and these averages are used to normalize
    data at test-time.
    At each timestep we update the running averages for mean and variance using
    an exponential decay based on the momentum parameter:
    running_mean = momentum * running_mean + (1 - momentum) * sample_mean
    running_var = momentum * running_var + (1 - momentum) * sample_var
    
    Input:
    - x: Data of shape (N, D)
    - gamma: Scale parameter of shape (D,)
    - beta: Shift paremeter of shape (D,)
    - bn_param: Dictionary with the following keys:
      - mode: 'train' or 'test'; required
      - eps: Constant for numeric stability
      - momentum: Constant for running mean / variance.
      - running_mean: Array of shape (D,) giving running mean of features
      - running_var Array of shape (D,) giving running variance of features
    Returns a tuple of:
    - out: of shape (N, D)
    - cache: A tuple of values needed in the backward pass
    """
    mode = bn_param['mode']
    eps = bn_param.get('eps', 1e-5)
    momentum = bn_param.get('momentum', 0.9)

    N, D = x.shape
    running_mean = bn_param.get('running_mean', np.zeros(D, dtype=x.dtype))
    running_var = bn_param.get('running_var', np.zeros(D, dtype=x.dtype))

    if mode == 'train':
        sample_mean = x.mean(axis=0)
        sample_var = x.var(axis=0)
        
        running_mean = momentum * running_mean + (1 - momentum) * sample_mean
        running_var = momentum * running_var + (1 - momentum) * sample_var
        
        std = np.sqrt(sample_var + eps)
        x_centered = x - sample_mean
        x_norm = x_centered / std
        out = gamma * x_norm + beta
        
        cache = (x_norm, x_centered, std, gamma)
        
    elif mode == 'test':
        x_norm = (x - running_mean) / np.sqrt(running_var + eps)
        out = out = gamma * x_norm + beta
    
    else:
        raise ValueError('Invalid forward batchnorm mode "%s"' % mode)

    # Store the updated running means back into bn_param
    bn_param['running_mean'] = running_mean
    bn_param['running_var'] = running_var

    return out, cache

3. メリット

Batch Normalizationを利用するメリットについては、以下のような議論がなされています。

大きな学習係数が使える

これまでのDeep Networkでは、学習係数を上げるとパラメータのスケール(大きすぎ、小さすぎ)が原因となって勾配消失・爆発(パラメータの更新が不安定となる現象)を引き起こすことが分かっていました。Batch Normalizationでは、各バッチで正規化を行うため、パラメータのスケールの影響を受けなくなります。
これにより大きな学習係数を設定できるようになり、学習の収束速度が向上します。

正則化効果がある

原論文でも、

・L2正則化の必要性が下がる
・Dropoutの必要性が下がる

というように、これまでの正則化テクニックを不要にできるという議論がなされています。
Dropoutは過学習を抑えますが学習速度が遅くなるため、Dropoutが不要になることで学習速度が向上します。
L2正則化にはハイパーパラメータの設定が必要であるため、この設計コストをなくすことが出来ます。

初期値にそれほど依存しない

バッチ正規化を用いることで、重みの初期値に対するモデルの感度が低下するため、ニューラルネットワークの重みの初期値がそれほど性能に影響を与えなくなります。

4. まとめ

今回はBatch Normalization(バッチ正規化)についてまとめていきました。
バッチ正規化を行うことにより、モデルはより高速かつ安定した計算を行うことができるようになります。

最後まで読んでいただきありがとうございました。

参考
(1) Batch Normalization：ニューラルネットワークの学習を加速させる汎用的で強力な手法
(2)Batch Normalizationを理解する
(3)Implementing Batch Normalization in Python
(4)Chainerを使ってコンピュータにイラストを描かせる