正規表現とオートマトン

正規表現とオートマトン

正規表現は、文字列のパターンマッチングを行うための汎用的な文法です。さまざまなプログラミング言語やコマンドラインツールなどで利用されています。

正規表現の理論的な背景として、オートマトンという概念があります。オートマトンは計算機科学の分野で研究されており、計算理論の教科書によく取り上げられています。ただ、いきなり教科書でオートマトンの説明を読んでも、わりと数学的な話で、プログラミングで扱っている正規表現のイメージとは少しギャップがあります。そこで本記事では、簡単な正規表現のマッチング処理のコードを書いてみて、オートマトンの概念をつかんでみます。

なお、コードを記述するプログラミング言語はなんでもよいのですが、本記事ではRustを使います。難しい文法は使わないので、Rustを知らなくても問題ありません。

正規表現のマッチング処理の素朴な実装

具体例として、正規表現 aba* のマッチング処理を考えてみましょう。素朴に考えて、与えられた文字列を先頭から順に1文字ずつ読み込んで処理することにします。まず、最初の文字が a であるかを判定します。そして、次の文字が b であるかを判定します。さらに次の文字があればそれが a であるかを判定します。それぞれの判定で異なる文字が来たらマッチング失敗です。読み込む文字がなくなるまで繰り返します。

状態遷移で考えると、もう少し整理できそうです。最初の状態を q0 とします。状態 q0 では次の文字が a なら状態 q1 に遷移します。状態 q1 では次の文字が b なら状態 q2 に遷移します。状態 q2 では次の文字が a ならそのまま状態 q2 にとどまります。どの状態でも、異なる文字が来たらマッチング失敗です。文字列を読み終わったとき、状態 q2 にいればマッチング成功です。

状態遷移図で書くと次のようになります。

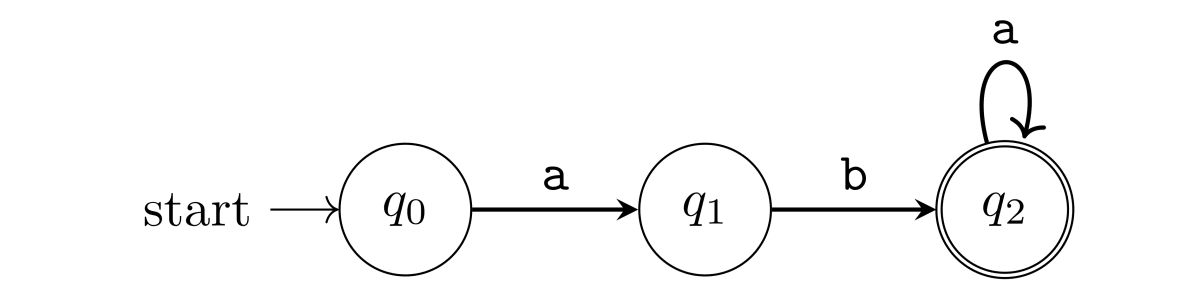
Rustで実装すると次のようになります。cargo コマンドでRustのプロジェクトを作成し、src/main.rs にコードを書きます。

fn accept(text: &str) -> bool {
    let mut current_state = 0;
    for ch in text.chars() {
        match current_state {
            0 => {
                if ch == 'a' {
                    current_state = 1;
                } else {
                    return false;
                }
            }
            1 => {
                if ch == 'b' {
                    current_state = 2;
                } else {
                    return false;
                }
            }
            2 => {
                if ch == 'a' {
                    current_state = 2;
                } else {
                    return false;
                }
            }
            _ => return false,
        }
    }
    current_state == 2
}

accept 関数は、与えられた text が正規表現 aba* にマッチしていれば true を返します。この accept 関数を使ったマッチングの判定を main 関数に書いてみます。src/main.rs に次のコードを書きます。

fn main() {
    let text = "abaaa";
    let matched = accept(text);
    if matched {
        println!("Matched!");
    } else {
        println!("Not matched!");
    }
}

また、accept 関数のテストコードも書いてみます。src/main.rs に次のコードを書きます。cargo test でテストを実行できます。

#[cfg(test)]
mod tests {
    use super::accept;

    #[test]
    fn test_accept_success() {
        assert!(accept("ab"));
        assert!(accept("abaa"));
    }

    #[test]
    fn test_accept_failure() {
        assert!(!accept("ba"));
        assert!(!accept("abac"));
        assert!(!accept("xyz"));
    }
}

別の具体例として、正規表現 a(b|c)+d のマッチング処理を考えてみましょう。次の状態遷移でマッチング処理ができます。

同様にRustで実装してみます。

fn accept(text: &str) -> bool {
    let mut current_state = 0;
    for ch in text.chars() {
        match current_state {
            0 => {
                if ch == 'a' {
                    current_state = 1;
                } else {
                    return false;
                }
            }
            1 => {
                if ch == 'b' || ch == 'c' {
                    current_state = 2;
                } else {
                    return false;
                }
            }
            2 => {
                if ch == 'b' || ch == 'c' {
                    current_state = 2;
                } else if ch == 'd' {
                    current_state = 3;
                } else {
                    return false;
                }
            }
            _ => return false,
        }
    }
    current_state == 3
}

正規表現 aba* と a(b|c)+d のマッチング処理を素朴に実装してみました。簡明なコードです。しかし、正規表現ごとに accpet 関数を実装する必要があります。

正規表現のマッチング処理の実装の共通化

accpet 関数の実装をもう少し汎用的にしてみましょう。先ほどの accept 関数の実装を見てみると、必要な情報は、状態遷移、初期状態、最終状態であることがわかります。これらをデータ構造として表現すると、次のようになります。

type Transitions = Vec<(char, usize)>;

struct StateMachine {
    transitions: Vec<Transitions>,
    initial_state: usize,
    final_state: usize,
}

Transitions 型は状態遷移をあらわしており、読み込んだ文字に対してどの状態に遷移するかを定義しています。StateMachine の transitions は、それぞれの状態のときの状態遷移 Transitions を定義しています。

おそらく、具体例を見たほうが分かりやすいでしょう。正規表現 aba* のマッチング処理の状態遷移を表現すると次のようになります。

StateMachine {
    transitions: vec![
        vec![('a', 1)],
        vec![('b', 2)],
        vec![('a', 2)],
    ],
    initial_state: 0,
    final_state: 2,
}

状態 0 のときの Transitions は vec![('a', 1)]、状態 1 のときは vec![('b', 2)]、状態 2 のときは vec![('a', 2)] となっています。

また、正規表現 a(b|c)+d のマッチング処理の状態遷移を表現すると次のようになります。

StateMachine {
    transitions: vec![
        vec![('a', 1)],
        vec![('b', 2), ('c', 2)],
        vec![('b', 2), ('c', 2), ('d', 3)],
        vec![],
    ],
    initial_state: 0,
    final_state: 3,
}

このデータ構造を用いた accept 関数は次のように書けます。

impl StateMachine {
    fn accept(&self, text: &str) -> bool {
        let mut current_state = self.initial_state;
        for ch in text.chars() {
            let current_transitions =
                self.transitions.get(current_state).unwrap();
            let transition = current_transitions
                .iter()
                .find(|(symbol, _)| ch == *symbol);
            match transition {
                Some((_, next_state)) => current_state = *next_state,
                None => return false,
            }
        }
        current_state == self.final_state
    }
}

一見すると for ループの中がごちゃついて見えますが、落ち着いて見るとやっていることは単純です。まず、現在の状態 current_state に対応する Transitions を取得します（get 関数）。そして、読み込んだ文字 ch に対応する遷移を探します（find 関数）。遷移が見つかれば次の状態に遷移します。遷移が見つからなければマッチング失敗です。

この実装によって、StateMachine を作成すれば正規表現のマッチング処理を実装できるようになりました。たとえば、正規表現 aba* のマッチング処理は次のように実装できます。

fn create_state_machine() -> StateMachine {
    StateMachine {
        transitions: vec![
            vec![('a', 1)],
            vec![('b', 2)],
            vec![('a', 2)],
        ],
        initial_state: 0,
        final_state: 2,
    }
}

fn main() {
    let state_machine = create_state_machine();
    let text = "abaa";
    let matched = state_machine.accept(text);
    if matched {
        println!("Matched!");
    } else {
        println!("Not matched!");
    }
}

正規表現 a(b|c)+d のマッチング処理は、作成する StateMachine を変更するだけで実装できます。

それぞれの正規表現に対応する StateMachine を作成する必要はあるのですが、accept 関数の実装が共通化できました。

オートマトン（DFA）

先ほどのデータ構造を理論的に定式化したものがオートマトンです。ここではとくに、決定性有限オートマトンについて説明します。以下、DFAと呼ぶことにします（Deterministic Finite Automatonの略）。

DFA（決定性有限オートマトン）とは、次の5つ組のことです。あえて数学の集合と写像の記法を用いますが、不慣れな人は軽く流していただいても大丈夫です。

• Q : 状態の有限集合。
• Σ : 入力文字の有限集合。
• δ : 状態遷移写像。δ : Q × Σ → Q（δ は Q の要素と Σ の要素を受け取って Q の要素を返す関数、という意味）。
• q0 : 初期状態。q0∈Q（q0 は Q の要素、という意味）。
• F : 受理状態の集合。F⊂Q（F は Q の部分集合、という意味）。

このDFAの定義をデータ構造として表現すると、次のようになります。

type State = usize;
type Symbol = char;
type Transitions = Vec<(Symbol, State)>;

struct Dfa {
    states: Vec<State>,
    alphabet: Vec<Symbol>,
    transitions: Vec<Transitions>,
    initial_state: State,
    final_states: Vec<State>,
}

先ほどの StateMachine とほとんど同じです。これも具体例を見てみます。正規表現 aba* のマッチング処理のDFAを表現すると次のようになります。

Dfa {
    states: vec![0, 1, 2],
    alphabet: vec!['a', 'b'],
    transitions: vec![
        vec![('a', 1)],
        vec![('b', 2)],
        vec![('a', 2)],
    ],
    initial_state: 0,
    final_states: vec![2],
}

accept 関数もほとんど同じ実装です。final_states が Vec<State> になっているので、最後のマッチング判定を次のように変更する必要がありますが、それだけです。

    self.final_states.contains(&current_state)

これで、正規表現のマッチング処理をDFAで実装できました。

正規表現から DFA への変換

正規表現のマッチング処理の実装にDFAが有益であると分かりました。しかし前提として、正規表現からDFAを作成する必要があります。そもそも、どんな正規表現に対してもDFAが定義できるのでしょうか。実は、正規表現とDFAは等価であることが知られており、どんな正規表現に対してもDFAが定義できます。ここでは、正規表現をDFAに変換する考え方の概要を説明します。

ここで、DFAを拡張したNFA（非決定性有限オートマトン）という概念を導入します。DFAは状態遷移の遷移先が一意的に定まりましたが、NFAは遷移先に複数の候補を許します。さらに、空文字を受け取って遷移する ε-遷移を許します（ε-遷移を許すものをとくに ε-NFAと呼んで区別することもあります）。正規表現をDFAに変換するには、中間にNFAを挟みます。

• 正規表現をNFAに変換します。
• NFAをDFAに変換します。

これらの変換について厳密な説明はここではしません。代わりに具体例を見て雰囲気をつかむことにします。正規表現 a(b|c)+d をDFAに変換する手順を見てみましょう。

まず、登場する文字 a b c d それぞれのマッチング処理の遷移を用意します。

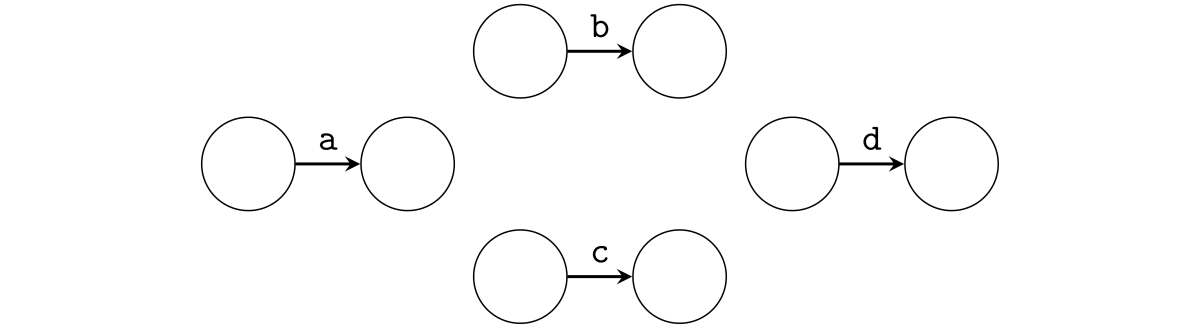
ここに ε-遷移を追加することで正規表現 a(b|c)+d を表現するNFAを作成していきましょう。まずは、選択演算 (b|c) を表現するための ε-遷移を追加します。

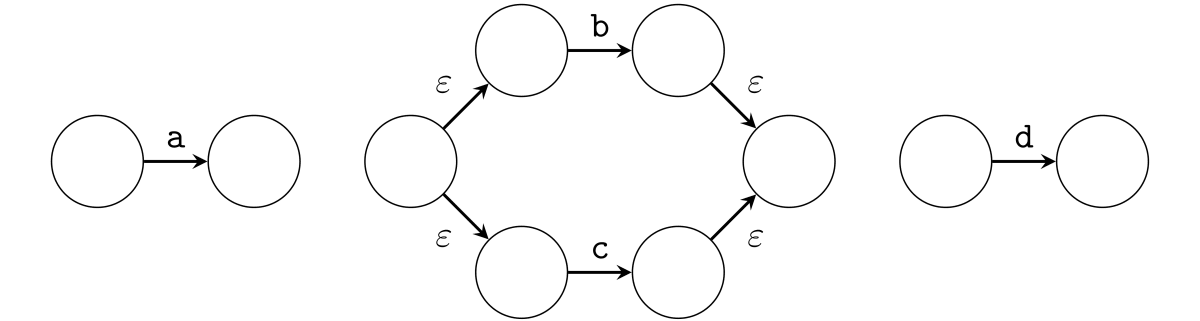
次に、繰り返し演算 (b|c)+ を表現するための ε-遷移を追加します。

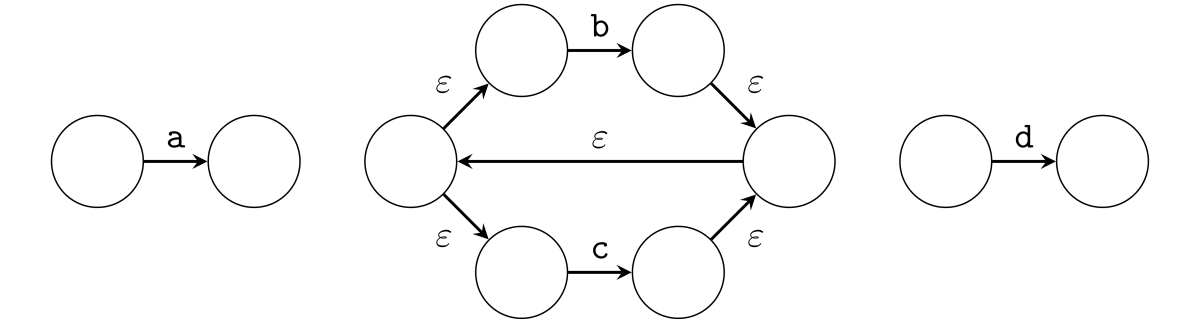
そして、連接演算 a(b|c)+d を表現するための ε-遷移を追加します。

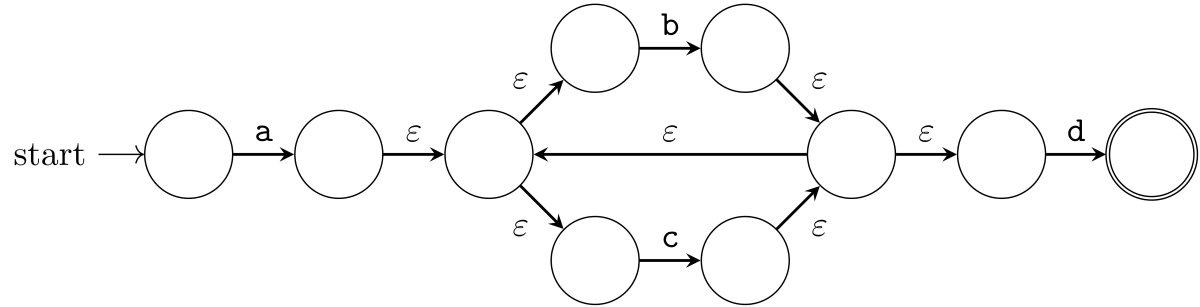
さらに初期状態と受理状態を決めて、正規表現 a(b|c)+d を表現するNFAが完成しました。

NFAからDFAに変換するのは機械的なアルゴリズムで行えます。まず、NFAの各状態から ε-遷移で到達可能な状態の集合（ε-閉包）を求めます。

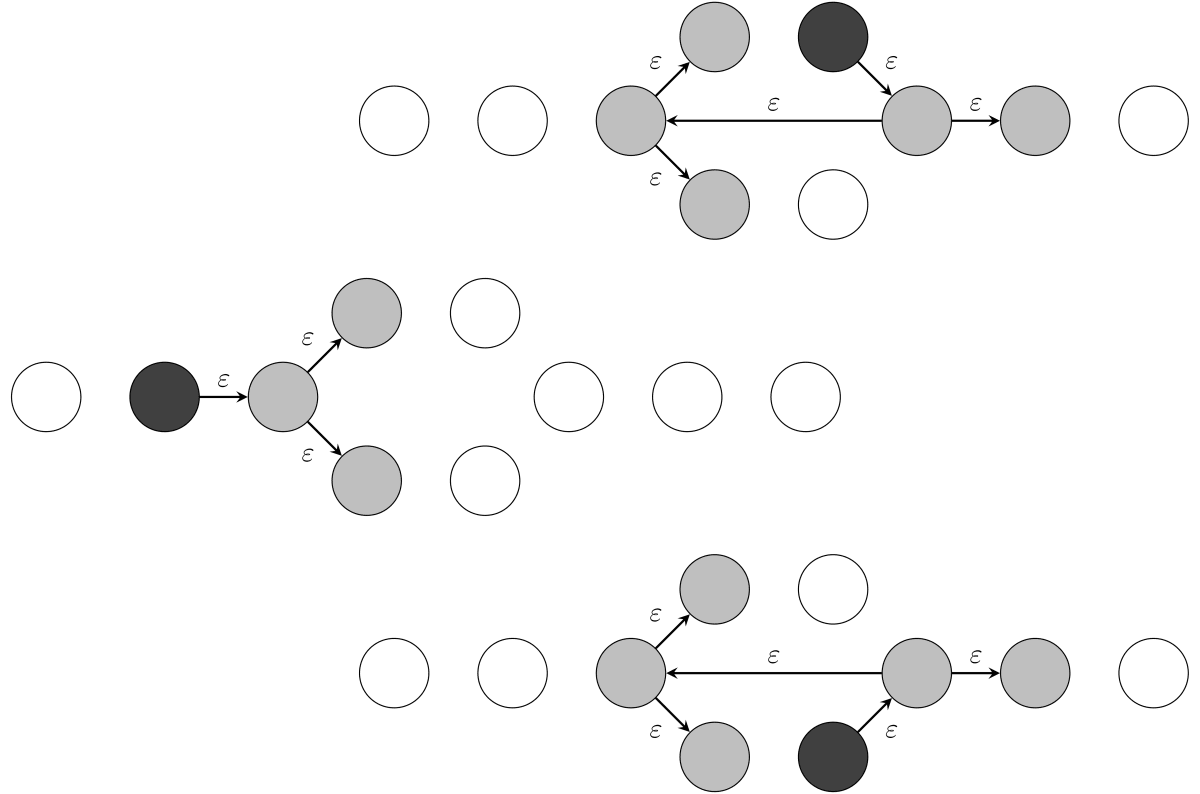
ε-閉包をひとつの状態に置き換えることで、ε-遷移を除去します。このアルゴリズムで ε-遷移を除去すると次のようになります。

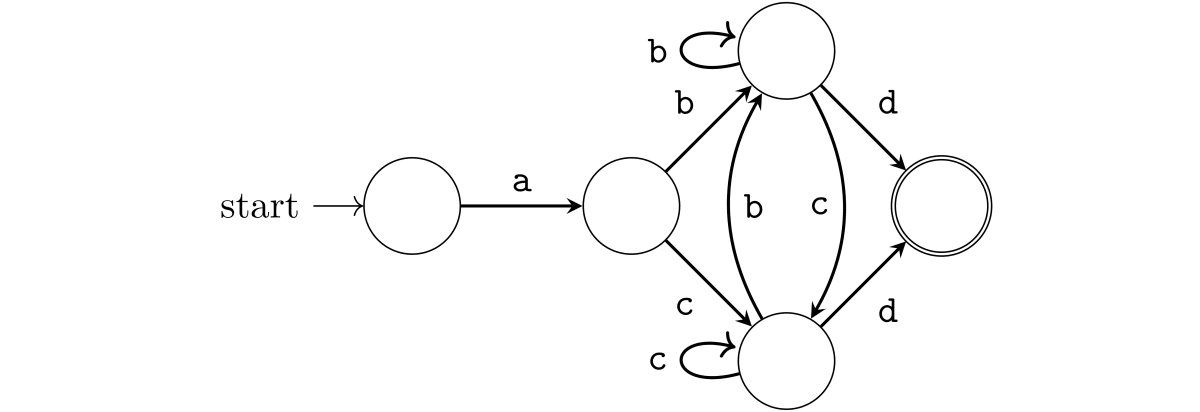
これでDFAができました。ただ、このDFAはもう少し小さくできます。具体的には、b を受け取った状態と c を受け取った状態は統合してひとつにできます。こうして最小化したDFAは次のようになります。

こうして、正規表現 a(b|c)+d を表現するDFAが完成しました。どんな正規表現でも、同じようなやり方でDFAに変換できます。その雰囲気をつかんでもらえたでしょうか。

まとめ

本記事の前半では、正規表現のマッチング処理の実装にDFAが有益であることを実際のコードを交えて説明しました。後半では、正規表現からDFAへの変換の考え方を説明しました。正規表現とオートマトンについて興味を持っていただければ幸いです。

参考文献

• J. ホップクロフト・R. モトワニ・J. ウルマン、オートマトン 言語理論 計算論 1、サイエンス社、2003
• 新屋良磨・鈴木勇介・高田謙、正規表現技術入門――最新エンジン実装と理論的背景、技術評論社、2015

ε-遷移を除去する際の ε-閉包の考え方は前者の書籍によります。後者の書籍では、ε-遷移を除去する際に ε-展開というアルゴリズムを用いています。少し考え方が異なるものの、同様の変換結果となります。

宣伝

本記事は技術書典で配布している「ゆめみ大技林 '23」に収録しています。他のメンバーの記事もありますので、ぜひご覧ください。