Photon Mappingの実装の記録

yumcyawiz

青い本、Photon Tracingで最初のDifufse面で格納して終わり or Diffuseに当たる度に格納(つまり1つのフォトンが複数回フォトンマップに格納されるか否か)のどちらなのかが不明確だが、p.103で

L(S|D)*Dがフォトンマップによって記述される全ての経路である.

とあるのでDiffuseに当たる度に格納する模様.

のp.17にもそのようにアルゴリズムが記述されている.

yumcyawiz

青い本、Photon Tracingでpdfで割る操作の記述がないが、そうしないとUnbiasedにならないはず
(おそらく青い本ではDiffuseでLambertと完全Specularしか扱っていないから分母分子で相殺されて出てこない)

pbrtだとそこら辺はちゃんと書いてあるし、そこそこの定式化もなされている.

もっと理論的にしっくりしたものないかなと思って論文探したらこれが良さそう.
https://doi.org/10.1145/2366145.2366210
カメラ側からのパスの生成において、密度推定を半径内の点サンプリングに置き換えていてなるほどなあという感じ. この論文はVCMなどの発展手法につながる.

yumcyawiz

kdtreeの実装
汎用的にしたいのでtemplate, C++20のconceptを使ってみる

struct Photon {
  Vec3 flux;
  Vec3 position;
  Vec3 wi;

  // implement Point
  static constexpr int dim = 3;
  float operator[](int i) const { return position[i]; }

  Photon() {}
  Photon(const Vec3& flux, const Vec3& position, const Vec3& wi)
      : flux(flux), position(position), wi(wi) {}
};

template <typename T>
concept Point = requires(T& x, int i) {
  { T::dim } -> std::convertible_to<int>;  // dimension
  { x[i] } -> std::convertible_to<float>;  // element access
};

template <typename PointT>
requires Point<PointT>
class KdTree {
 private:
  struct Node {
    int axis;           // separation axis(x=0, y=1, z=2)
    int idx;            // index of median point
    int leftChildIdx;   // index of left child
    int rightChildIdx;  // index of right child

    Node() : axis(-1), idx(-1), leftChildIdx(-1), rightChildIdx(-1) {}
  };

  std::vector<Node> nodes;  // array of tree nodes
  const PointT* points;     // pointer to array of points
  int nPoints;
};

yumcyawiz

Photon Tracingで光源から飛ばすフォトンのthroughputをどう初期化するか.

$x_0$ : 光源上でサンプリングされた点
$x_1$ : Photon Tracingで最初にヒットした点
$p(x_0)$ : 光源上の点サンプリングのpdf
$p(\vec{\omega_0})$ : 光源上での方向サンプリングのpdf
$\beta(x_0, x_1)$ : 点 $x_0$ から点 $x_1$ までのthroughput

throughputは以下のようにすれば良い(https://pbr-book.org/3ed-2018/Light_Transport_III_Bidirectional_Methods/Stochastic_Progressive_Photon_Mapping#eq:particle-weight-definition)

\beta(x_0, x_1) = \frac{L_e(x_0, \vec{\omega_0})G(x_0,x_1)}{p(x_0)p(x_1)}

ここで密度関数の変換公式

p(x_1) = \frac{\cos{\theta_1}}{r^2}p(\vec{\omega_0})

を使うと

\beta(x_0, x_1) = \frac{L_e(x_0, \vec{\omega_0})}{p(x_0)p(\vec{\omega_0})}\cos{\theta_0}

yumcyawiz

Photon Tracingを実装したのでPhoton Mapを可視化してみる.
カメラ側からレイを飛ばし、最初の交差点の近傍にあるPhotonのthroughputをそのまま画像にする.
なんか偏っている気がする. というか光源部分が光ってしまっているのはおかしい.

yumcyawiz

光源上の点での方向サンプリングがバグっていた
修正すると以下のような画像が得られた。それっぽい

yumcyawiz

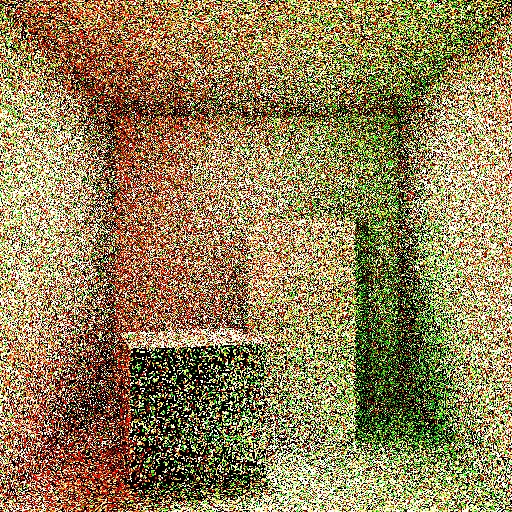
カメラからレイトレをし、点 $x$ に到達したとする.
この点から方向 $\vec{\omega_o}$ に反射される放射輝度は近傍Photonを用いて以下のように計算できる.

$N_p$ : 追跡したPhotonの合計数(近傍Photonの数ではない点に注意)
$N_{neighbor}$ : 近傍Photon数
$r$ : 近傍Photonの点 $x$ からの最大距離
$\vec{\omega_j}$ : $j$ 番目の近傍Photonの入射方向
$\beta_j$ : $j$ 番目の近傍Photonのthroughput

L(x, \vec{\omega_o}) \approx \frac{1}{N_p \pi r^2}\sum_{j=1}^{N_{neighbor}} f(x,\vec{\omega_j}, \vec{\omega_o})\beta_j

この式は以下で単位円上で定数となるようなカーネルを用いたものに対応する.

yumcyawiz

絵は出るようになったがなんか暗い
Path Tracingのリファレンスと比べても明らかに暗い

yumcyawiz

maxDepth=1でPath Tracingのリファレンスと比較するとBiasなさそうに見える
ということはPhoton Tracingのdepth > 1以降で何かがおかしい.

yumcyawiz

色々バグっていたので修正したところPath Tracingのリファレンスとよく一致してきた.
色ムラが見えるのは直接照明もPhoton Map経由で計算しているためだと思われる(間接照明のみPhoton Mapで計算することが多い)

なおバグは

Photon Tracing時のPhotonの追加, 乱数生成がスレッドセーフでない
KdTreeのK最近傍探索でqueueをpopし忘れて同じノードしか返ってこない

など. Throughputの計算は問題なさそうだった.

(フォトン数: 1000000, 密度推定に使うフォトン数: 100)

yumcyawiz

なお密度推定に使うフォトン数を1(つまり最近傍にあるフォトンしか使わない)にすると以下のようになる。ノイズが多くてパストレっぽい感じの見た目になる。

影になっている部分はフォトン密度が割とスカスカなのが分かる。

yumcyawiz

$d$ 次元でのカーネル密度推定は $\int_{\mathbb{R}^d} K(x)dx = 1$ となるような関数 $K$ を用いて

\hat{p}(x) = \frac{1}{nh^d}\sum_{i=1}^n K\bigg(\frac{x_i - x}{h}\bigg)

で与えられる.

この式からPhoton Mappingで使われるような $k$ 最近傍を用いた密度推定の式がどう導かれるのか気になっていたが、 $h$ を $x$ や $x_i$ に依存させたVariable Kernel Density Estimationというものがあるらしい。

Terrell, George R., and David W. Scott. "Variable kernel density estimation." The Annals of Statistics (1992): 1236-1265.

この論文中では $h$ を $x$ に依存させた密度推定をBalloon Estimatorと呼んでいて、以下のような形になる。

\hat{p}(x) = \frac{1}{nh(x)^d}\sum_{i=1}^n K\bigg(\frac{x_i - x}{h(x)}\bigg)

そしてPhoton Mappingで使われるような $k$ 最近傍を用いた密度推定はBalloon Estimatorにおいて $K$ を $d$ 次元球面上の一様分布の密度関数とすることで表されることが書いてある。

$d=2$ の場合なら単位円上の密度関数は $\frac{1}{\pi}$ なので

\hat{p}(x) = \frac{k}{n\pi h_k(x)^2}

となる。ここで $k$ 最近傍以外の点による総和の寄与は0であるので分子は $k$ になる。この形の推定量はLoftsgaarden-Quesenberry Estimatorと言うらしい。

Loftsgaarden, Don O., and Charles P. Quesenberry. "A nonparametric estimate of a multivariate density function." The Annals of Mathematical Statistics 36.3 (1965): 1049-1051.

なおBalloon Estimatorは論文中に

When Applied globally, the esimate typically does not integrate to 1 and thus is usually not itself a density, even when $K$ is.

とある通り、一般的に推定した密度関数が積分して1にならないらしい。これがPhoton Mappingのバイアスの出処なのかなと思ったりする。

yumcyawiz

直接照明の計算は明示的な光源サンプリング(Next Event Estimation)、間接照明の計算はFinal Gathering(さらにレイを飛ばしてその先でPhoton Map使って放射輝度推定)にしてみた。

以下はFinal Gatheringやらない、やる場合の比較。
Final Gatheringやるとバイアスが目立たなくなることが分かる。

ここら辺の話は青い本だと8.2.1, 9.4辺りに書いてある。

pbrtだと

For diffuse surfaces, it’s generally worth using photons, though it can be worthwhile to trace one last bounce. This approach is called final gathering; if photons are used only after a diffuse bounce, then any errors from insufficient photon density are generally less visible, though more camera paths may need to be traced to eliminate noise. (See Exercise 16.8 for further discussion of final gathering.)

Christensen, Per H. "Faster photon map global illumination." Journal of graphics tools 4.3 (1999): 1-10.

の1.3も分かりやすい.

yumcyawiz

Final gatheringで完全鏡面のあるシーンをレンダリングしたところ以下のように暗くなってしまった。

左: Final gatheringなし
真ん中: Final gatheringあり
右: Path tracing

何故こんなことが起きるかというと、Final gatheringではLSDEのようなパスを表現できないため。Final gatheringでレイを飛ばした先がSpecularだとそこにはPhotonがないため放射輝度の推定ができない。

そこで集光模様フォトンマップ(Caustics Photon Map)を別に用意する必要がある(青い本 9.3.1)。集光模様フォトンマップはSpecularに当たった後にDiffuseに当たったPhotonを格納する。

Final gatheringを使う時のレンダリングでは集光模様フォトンマップからの放射輝度推定も加える。するとLSDEのようなパスも表現できるようになる。

以下はFinal gatheringありの時に集光模様フォトンマップを使うようにした場合。

暗くなっているのが改善されているのが分かる。しかしバイアスが目立つ。完全鏡面のようにSpecularでフォトンが拡散してしまうような場合は相性が良くないのかもしれない。

yumcyawiz

ガラス球のシーンで比較したもの。

パストレの方が分散低い気がする。特にPhoton Mappingではガラス面に写り込んだ光源が綺麗に描画できていない。これはガラス面で反射か屈折かのRussian Rouletteをしているが、それのサンプル数が足りないため。

サンプル数をパストレと同じ10000に設定してしまうとPhoton Mappingの計算時間がとても長くなってしまう。

青い本では綺麗に描画しているが、どうやっているんだろう? Russian Rouletteやらずに2本のレイを追跡しているのか?

yumcyawiz

Pocolさんの実装を見るとdepthが浅いところでは反射と屈折の両方追跡していることが分かる。

一般的に $n$ 個の複合BRDFの場合はどうするのがベストなんだろう。普通はガラスみたいにデルタ関数 + デルタ関数の組み合わせじゃないからランダムサンプリングでもうまくいくんだろうか。

yumcyawiz

Final Gatheringやった場合の完全鏡面のシーンがリファレンスと比べてまだ暗いことに気づいた。
以下はリファレンスとの差分。球の下辺りに若干差がある。

これは集光模様フォトンマップを作成する時にSpecularに当たった後の最初のDiffuse面でPhotonの追跡を打ち切ってしまっているため、LSDSDEのようなパスをFinal gathering時に表現できないことが原因だった。

打ち切りをやめたらリファレンスと一致した。

青い本を見ると集光模様フォトンマップはSpecularに当たった後の最初のDiffuse面で打ち切って良いと書いてあるが、本が間違っているのか自分の実装が何か違うのかは分からない。

yumcyawiz

Final GatheringでIndirect Illumination計算する時に、飛ばしたレイが当たった場所がSpecularの時は再帰的に追跡して、最終的に当たったどこかのDiffuse面で密度推定やるようにしたら、Caustics Photon Map作成時にSpecularに当たった後の最初のDiffuse面でPhotonの追跡を打ち切ってもリファレンスと一致するようになった。

つまりこの方法でもLSDSDEみたいなパスが表現できている。

青い本は明示的に書いてないけどこれをやっているんではないだろうか。

yumcyawiz

モデル読み込みを実装し、水入りコーネルボックスをレンダリングしてみた。
Causticsがめちゃくちゃ綺麗に出てくれて感動

yumcyawiz

別の水入りコーネルボックス。
ガラス下の部分がパストレと比べて明るい。

原因はCaustics Photon Map作成時にLS+Dではなく、LDSのようなパスも含めてしまっていることだった。これによってLDSDSEのようなパスがFinal Gatheringでダブルカウントされる。

修正したがまだ明るいように見える。まだダブルカウントしているパスがあるんだろうか。

yumcyawiz

とりあえず一段落したので実装を公開

yumcyawiz

Shockerさんとholeさんからガラス下の明るさがリファレンスと一致しないのは、BTDF評価時のScalling Factor辺りに原因があるのではないかという意見をもらった。

Veach, Eric. Robust Monte Carlo methods for light transport simulation. Stanford University, 1998.

の5.2や

が参考になる。

放射輝度の補正は視点からトレーシングする時だけ行い、Photon Tracing時には放射輝度の補正を行ってはいけないことが書いてある。

この修正を入れたところリファレンスと一致するようになった。

yumcyawiz

Shading Normal(頂点法線をUV座標で補完して算出する法線)を使っている場合、反射方程式は以下の形になっている。

$N_s(x)$ : 点 $x$ でのShading Normal

L_o(x, \vec{\omega_o}) = \int_{\Omega}f_{N_s}(x, \vec{\omega_i}, \vec{\omega_o})L_i(x, \vec{\omega_i})|N_s(x)\cdot\vec{\omega_i}|d\sigma(\vec{\omega_i})

ここで元々の反射方程式のCosine項はGeometric Normal(三角形の面法線)が使われるべきである。例えばShading Normalは実際の物体形状と一致していないので投影面積は実際とずれてしまう。

反射方程式をGeometric Normalで書き直してあげると

$N_g(x)$ : 点 $x$ でのGeometric Normal

L_o(x, \vec{\omega_o}) = \int_{\Omega}f(x, \vec{\omega_i}, \vec{\omega_o})L_i(x, \vec{\omega_i})|N_g(x)\cdot\vec{\omega_i}|d\sigma(\vec{\omega_i})

Shading Normalを使った最初の式は本来これになるべきである。そこで2つの式を一致させるために $f_{N_s}$ をいじると

f_{N_s}(x, \vec{\omega_i}, \vec{\omega_o}) = f(x, \vec{\omega_i}, \vec{\omega_o})\frac{|N_s(x)\cdot\vec{\omega_i}|}{|N_g(x)\cdot\vec{\omega_i}|}

Shading Normalを使う時はこのBSDFを使うべきである。カメラ側からトレーシングする場合はこれを反射方程式に代入してあげると、単純にBSDFやコサイン項をShading Normalで評価するだけで良いので、特に既存の処理に変更を入れる必要はない。

一方でPhoton Tracing時にはBSDFの形が $\vec{\omega_i}$ , $\vec{\omega_o}$ に関して非対称となっているため注意する必要がある。試しに $\vec{\omega_i}$ , $\vec{\omega_o}$ を入れ替えてみると

f_{N_s}(x, \vec{\omega_o}, \vec{\omega_i}) = f(x, \vec{\omega_o}, \vec{\omega_i})\frac{|N_s(x)\cdot\vec{\omega_o}|}{|N_g(x)\cdot\vec{\omega_o}|}

これをGeometric Normalを使った反射方程式に代入すると

L_o(x, \vec{\omega_o}) = \int_{\Omega}f(x, \vec{\omega_i}, \vec{\omega_o})L_i(x, \vec{\omega_i})\frac{|N_s(x)\cdot\vec{\omega_o}|}{|N_g(x)\cdot\vec{\omega_o}|}|N_g(x)\cdot\vec{\omega_i}|d\sigma(\vec{\omega_i})

カメラ側からトレーシングする場合と異なり、 $\frac{|N_s(x)\cdot\vec{\omega_o}|}{|N_g(x)\cdot\vec{\omega_o}|}|N_g(x)\cdot\vec{\omega_i}|$ という項が現れていることが分かる。Photon Tracing時にはこの項をコサイン項として使わなければならない。

実際使わないとリファレンスと若干差異が出てしまう。以下の画像では左下の集光模様がリファレンスと比べてボヤけてしまっているのが分かる。

コサイン項の補正を入れてあげると以下のようにリファレンスに近づく。

参考資料

Veach, Eric. Robust Monte Carlo methods for light transport simulation. Stanford University, 1998 の5.3

yumcyawiz

下の画像では完全鏡面の球の右下辺りがリファレンスと比べて若干明るくなっていることが判明。

これはLight leakによるものだということが分かった。

これを防ぐようにしたところ、明るさは減って大体リファレンスと一致した。

yumcyawiz

色々とハマりポイントがあるので、それっぽい見た目が出てもなかなか安心できない。信頼できるリファレンスと比較することの重要性を感じる。

このスクラップは2021/11/29にクローズされました