Zenn
📚

Pythonの整数型はどのように実装されているのか

2021/12/29に公開
Python
#
翻訳
tech

この記事はPython Advent Calendar 2021 18日目の記事です。

GoogleでソフトウェアエンジニアをしているAlberto Oshiro氏のHow Python Represents Integers using Bignumの翻訳になります。本人のご了承を得て公開しています。感謝。


Photo by Crissy Jarvis on Unsplash

C/C++のような低レイヤーのコーディングをしているプログラマは整数型のメモリ使用量を気にしなければいけません。また、オーバーフローを防ぐために変数の取りうる最小・最大値も把握して、intで十分なのか、longが必要なのかを常に考えなければいけません。

C/C++と違ってPythonの整数値にはオーバーフローがないので、Pythonプログラマは整数にどの型を使うか考える必要はないです。また、Pythonの整数型はとてつもなく大きい数を演算しても精度が失われることはないです。唯一の制限はマシンのメモリ不足(つまりハードウェアによる制限)だけです。

実際に階乗(Factorial)を計算する例をみてみましょう。Pythonでは外部のライブラリを使わずに結果の大きさに関わらず階乗を計算することができます。

def factorial(n):
   if n == 0 or n == 1:
     return 1
   return n * factorial(n-1)

factorial関数に231を入力するとPythonがどれほど大きい整数値を扱えるか分かるでしょう。

>>> factorial(231)
1792233667382633521618843263044232513197622942259968207385215805123682159320161029848328112148883186161436034535802659466205111867109614573242316954383604389464524535467759401326264883566523043560811873179996072188155290081861628010250468430411854935707396605833540921031884571521279145124581094374547412403086564118143957940727734634769439112260383017302489106932716079961487372942529947238400000000000000000000000000000000000000000000000000000000

整数値表現

この記事はもっとも一般的に使われている処理系であるCPythonのでの話になります。他の処理系での整数型の表現は異なるかもしれません。CPythonを使う利点として、CPythonのコードベースがGithubで自由に見れることにあります。

Python3以降では全ての整数値は以下のstructで表現されます。

struct _longobject {
   PyObject_VAR_HEAD
   digit ob_digit[1];
};

マクロを展開すると以下のようになります。

struct {
   sssize_t ob_refcnt;
   struct _typeobject *ob_type;
   ssize_t ob_size;
   uint32_t ob_digit[1];
};

最初の二つのフィールドは重要ではないです。ob_refcntはPythonのGCで使われ、ob_typeは型のIDを表します。この場合は整数になります。

整数値は残り二つのフィールドob_digit, ob_sizeで表します。ob_digitは整数値の各桁を格納します。ob_sizeはdb_didit配列の長さと整数値の符号(正か負)の2つを格納します。

このように整数値の各桁を文字列もしくは配列で表すことを任意精度演算(Bignum Arithmetic)[1]といいます。

2^30進数

uint32_tの配列を整数値表現に使うことを考えてみましょう。Pythonは実用性と効率性から多くのビルトイン関数ではある特殊なビットが必要なので、32ビット全てを使うことができないです。CPythonのリポジトリにはこの制限についてコメントがありますので、興味がある方は見てみてください。

Pythonは32ビットのうち30ビットしか使えないので、全ての整数値を2^30進数で表します。結果、uint32_tの配列のそれぞれの要素は0から1073741823 (2^30-1)の値になります。ob_sizeは2^30進数の配列の長さを表します。

配列表現はリトルエンディアン、つまり一番小さい数が先に来ます。例えば10進数を例にして考えると、234という数字を配列には<4,3,2>のように逆に格納することになります。

例えば234254646549834273498という整数値を2^30進数に変換してみます。2^30進数を表現するには記号が足りないので、ここは10進数で表現することにします。234254646549834273498という整数値は462328538,197050268,203(462328538は最初のdigit,次に197050268, 最後のdigitが203)になります。digitsはこのように整数値に戻すことができます。

>>> 462328538*(2**30)**0 + 197050268*(2**30)**1 + 203*(2**30)**2
234254646549834273498L

234254646549834273498という整数値はPythonでは2^30進数を使って462328538,197050268,203というdigitsで表されstructフィールドは以下のようになります。

最適化

任意長整数を使った整数値の表現や演算は実行時のコストがかかります。Pythonのint型はイミュータブルなので、Pythonインタプリタはプログラム実行前に-5から256までの全ての数をあらかじめ作っておき、必要になった時に利用します。

任意長整数を使う明確なデメリットはメモリ使用量です。Pythonではいかなる整数値も少なくとも28バイト必要になり、これはC言語の7から14倍になります。

任意長整数の加算

任意長整数演算のメリットは演算のシンプルさにあります。この記事は加算しか説明しませんが、他の演算も基本は同じです。任意長整数の加算は10進数の時に紙と鉛筆でするときと同じです。まずは一番小さい桁を加算し、その後は次の桁へと計算を移していきます。各桁の計算結果は次の桁へ持ち越されます。

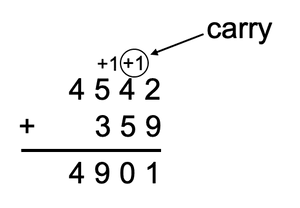
Pythonの任意長整数演算は配列を使ってこの計算を行います。演算対象の二つの数の配列の各要素を加算し、桁を超えた場合は次の桁へ持ち越しします。このアルゴリズムは配列要素0から始まり、小さい方の配列の長さまでイテレートします。まず、空の配列を作りますが、この配列は演算対象の二つの数のうち大きい方より一つだけ要素数が大きくします。9と93(加算結果は102)を例に考えると、大きい方の数値93は2桁あるので計算結果は3桁持つことになります。計算結果が大きい方の桁数と同じになる場合(e.g. 1 + 93 = 94)は計算後に配列を縮めます。

任意長整数の加算を二つの数234254646549834273498と23425464654983を例に図解していきます。

234254646549834273498のstructは以下のようになります。

23425464654983のstructは以下のようになります。

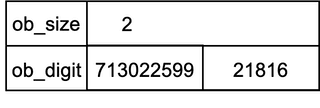
加算アルゴリズムはまず要素数4のからの配列を作ります(大きい方の数値234254646549834273498の配列より一つ大きい要素数)

次に各桁を加算していきます。

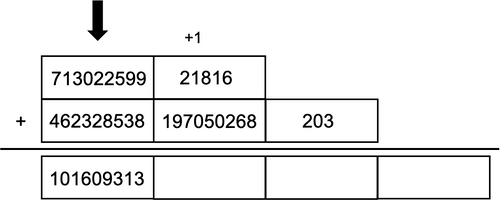
左から初めて小さい方の配列の長さまでイテレートし終わったら、このような途中結果になります。

最後に配列サイズを一つ減らすと、加算結果は以下のように表せることができました。

CPythonのコードはC言語ですが、この加算演算をPythonで表すとこのようになります。

base = 2**30

def add(x, y):
    # making sure x is larger than y
    if len(x) < len(y):
        x, y = y, x

    # result list is one digit longer than x
    z = [0] * (len(x) + 1)
    carry = 0
    i = 0
    while i < len(y):
        total = x[i] + y[i] + carry
        z[i] = total % base
        carry = total // base
        i += 1

    while i < len(x):
        total = x[i] + carry
        z[i] = total % base
        carry = total // base
        i += 1

    z[i] = carry
    # removing leading 0's.
    if z[i] == 0:
        z = z[:-1]
  
    return z

おわりに

Pythonは整数値に任意長整数を使っています。JavaやC/C++等の言語と比べてPythonでの整数値はとても使いやすくなっています。他の言語ではプログラマがどの型を使うのか考えないといけないですが、Pythonは抽象化してくれています。その反面、Pythonの整数値はメモリ使用量的に不利というでもリットもあります。C言語では2か4バイトで整数値を扱えたのに対し、Pythonでは最低28バイトも必要になります。簡単なスクリプトではこの程度の差異は無視できますが、もっと大きなデータを取り扱うプログラムではC言語のようなプログラミング言語を使った方が良いかもしれません。

References

脚注

  1. 任意精度演算 ↩︎

GitHubで編集を提案

Discussion