📊

統計検定1級チートシート

に公開
統計学
数理統計
統計検定
idea

A. 統計検定®︎1級とは

  • 日本統計学会が認定する最難関レベルの統計資格
  • 大学専門課程修了レベルで、データ解析に用いる統計学の基礎能力をはかる
  • 確率論・推定/検定理論・ベイズ統計・回帰分析・多変量解析などを網羅
  • 統計数理(5問中3問選択)・統計応用(人文科学/社会科学/理工学/医薬生物学から1問選択)から成る
  • 合格率は20%前後。一般に300H程度の勉強が必要(らしい)

B. 本稿の目的

  • 統計検定1級合格までの過程で、当方が頭の中でシンプルにまとめた内容を備忘録として残す。
  • 統計検定の問題を解くうえで必要であった公式を、本稿の執筆をもって改めて整理する。
    • ※1 あくまで以下のチートシートは最低限必要な事項
    • ※2 これらの数式を丸暗記ではなく、定義から導出できるようにし、試験で扱えるように理解する

C. チートシート

1. 基本式定義
  • 離散/連続確率分布の定義
\begin{aligned} P(X=x) &= f_X(x) \qquad\quad\quad\ \ \ \text{[discrete]} \\[5pt] P(X\leq x) &= \int_{-\infty}^x f_X(t) dt \qquad \text{[continuous]} \end{aligned}
  • 期待値の定義
\mathbb{E}[g(X)] = \begin{cases} \sum\limits_{x} g(x) f_X(x) & : \text{[discrete]} \\ \int g(x) f_X(x) \,dx & : \text{[continuous]} \end{cases}
  • 分散の定義
\sigma^2_X=\text{Var}[X]=\mathbb{E}[(X-\mathbb{E}[X])^2]
  • モーメント母関数
m_X(t)=\mathbb{E}[e^{tX}]
2. 多変数への拡張
  • 和・積の法則
\text{I}:\,f_X(x) = \int f_{X,Y}(x,y) \, dy \qquad \text{II}:\,f_{X,Y}(x,y) = f_{X|Y=y}(x) f_Y(y)
  • 共分散・相関係数
\text{Cov}(X,Y) = \mathbb{E}_{X,Y} [(X - \mu_X)(Y - \mu_Y)] \qquad \rho = \frac{\text{Cov}(X,Y)}{\sigma_X \sigma_Y}
  • 反転・全分散の公式
\mathbb{E}[X] = \mathbb{E}_{\textcolor{orange}{Y}} \left[ \mathbb{E}_X [X | \textcolor{orange}{Y}] \right] \qquad \text{Var}[X] = \mathbb{E}_Y \left[ \text{Var}[X | Y] \right] + \text{Var} \left[ \mathbb{E}_X [X | Y] \right]
  • 変数変換
f_{U,V}(u,v) = f_{X,Y} \big( x(u,v), y(u,v) \big) \left\| \begin{matrix} x_u & x_v \\ y_u & y_v \end{matrix} \right\|
3. 確率分布間の関係

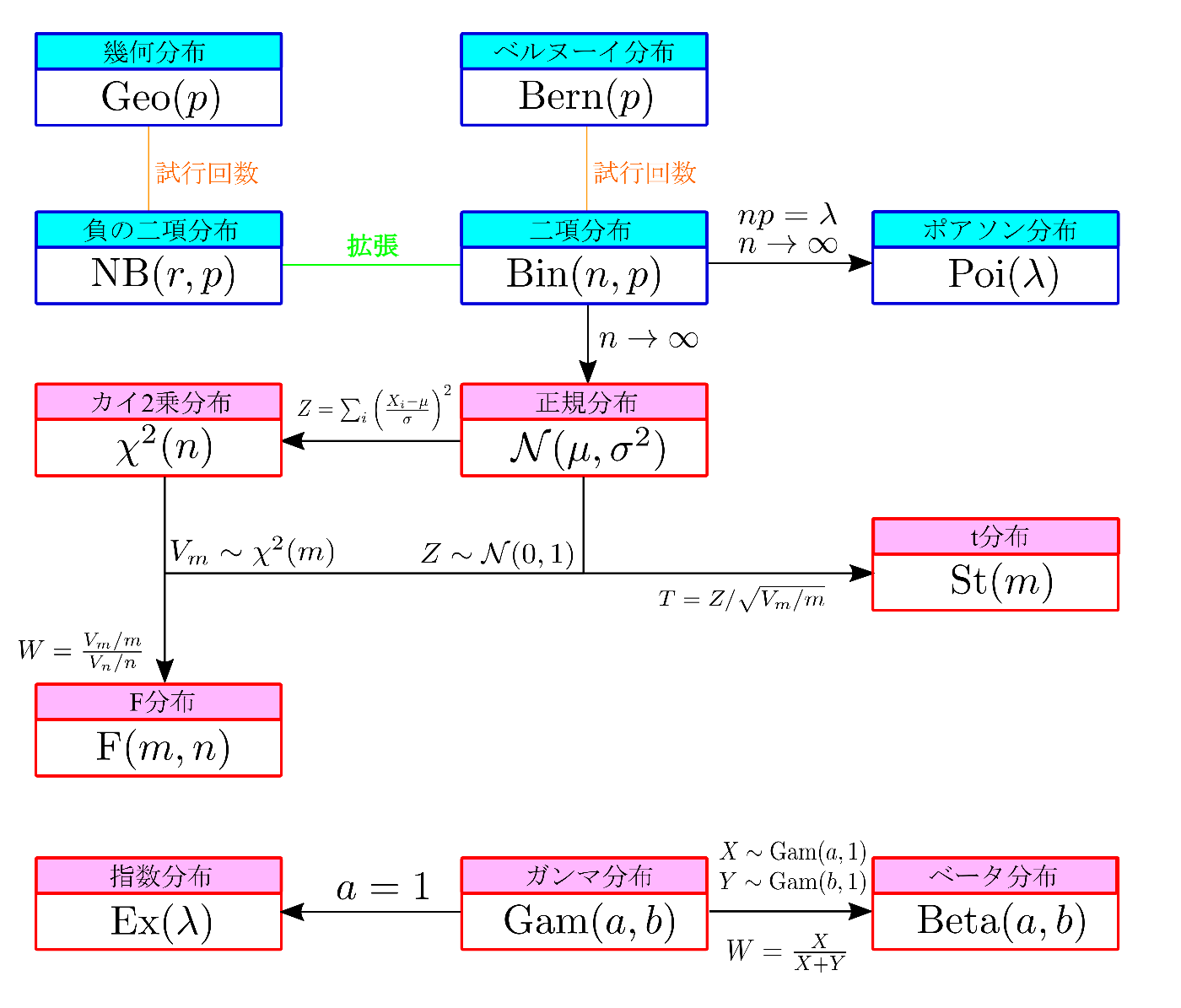
4. 標本統計
  • 標本統計量(平均・分散・普遍分散)
\text{I}: \quad \bar{X} \equiv \frac{1}{n} \sum_{i=1}^{n} X_i \quad \quad \text{II}: \quad S^2 = \frac{1}{n} \sum_{i=1}^{n} (X_i - \bar{X})^2 \quad \quad \text{III}: \quad U^2 = \frac{1}{n-1} \sum_{i=1}^{n} (X_i - \bar{X})^2
  • 検定統計量
\text{I}: \quad V_{n-1} = \frac{(n-1) U^2}{\sigma^2} \sim \chi^2(n-1) \quad \text{II}: \quad \frac{\bar{X} - \mu}{U / \sqrt{n}} \sim \text{St}(n-1) \quad \text{III}: \quad \frac{V_m / m}{V_n / n} \sim F(m,n)
  • チェビシェフの不等式
P(|X-\mu|\geq \varepsilon)\leq \frac{\text{Var}[X]}{\varepsilon^2}
  • 中心極限定理
\textcolor{red}{\sqrt{n} (\bar{X} - \mu) \xrightarrow{d} \mathcal{N}(0, \sigma^2)}
5. 推定
  • 十分統計量・フィッシャーの分解定理
f_n(x; \theta) = h(x) g(T(x); \theta)
  • 対数尤度
\ell(\theta, x) = \log f_n(x; \theta) = \log \left[ \prod_{i=1}^{n} f(x_i; \theta) \right]
  • モーメント法
\mu_k = \mathbb{E} [X^k] = \frac{1}{n} \sum_{i=1}^{n} (X_i)^k
  • フィッシャー情報量
J_n(\theta) = \mathbb{E} \left[ \left\{ \frac{\partial}{\partial \theta} \log f_n(X; \theta) \right\}^2 \right] = - \mathbb{E} \left[ \frac{\partial^2}{\partial \theta^2} \log f_n(X; \theta) \right]
  • クラメール・ラオの不等式
\text{Var}[\hat{\theta}] \geq J_n(\theta)^{-1}

Discussion