🗿

正規表現の"正規"とは何か気になったら正規表現の歴史を紐解くことになってしまった話

2021/10/31に公開

2件

正規表現

idea

正規表現の"正規"って何

ある時ふと思いました。
「正規表現の"正規"って何だろう？」
「何を根拠に"正規"を名乗っているのか？」
と。

「誰かが『これが正規の表現だ』と言ったはず」で、
「それは周りにどうやって"正規"だと認められたのだろう」
ということが気になったので調べてみました。

this_is_regular

"正規表現"という名前でなくて、"ジャックさんの表現"とか"記号ごちゃごちゃ表現"だったらこんな疑問も持たなかったのですけど。

数学における"正規"とは

一般に"正規"というと、"正規品"や"正規の手順"といったように"本物の(genuine)"や"公式な(official)"といった意味がありますが、数学の"正規"はちょっと違います。

数学で"正規"(および"正則"、英語では"regular"または"non-singular")は、ある概念に強い制限をかけたもの、という意味です。強い制限をかけたものは取り扱いが楽になります。分野によって"正規"の定義は異なります。
例えば、正則行列は、逆行列を持つ正方行列という意味です。
データベースの正規化はデータの持ち方に制約をかけています。

https://ja.wikipedia.org/wiki/正則

ということは、正規表現とは、"表現のうち、強い制約がかかったもの"ということができそうです。
ところで"表現"って何？

正規表現の"表現"って何

Wikipediaの正規表現ページに

正規表現（せいきひょうげん、英: regular expression）は、文字列の集合を一つの文字列で表現する方法の一つである。

と書いてあります。正規表現の"表現"とは"文字列の集合を一つの文字列で表現する方法"のことのようです。

つまり、正規表現とは、"文字列の集合を一つの文字列で表現する方法のうち強い制約がかかったもの"と言えそうです。

"強い制約"とは何でしょう。それを説明する前に一旦正規表現の歴史を紐解いていきましょう。

チューリング機械

チューリング機械は、1936年にイギリスの数学者チューリングが考えた、仮想の計算機械です。

チューリング機械は、無限に長いテープ、ヘッド(読み込み部分)、制御部、の三つの部分を持ちます。制御部は、有限個の状態を持ち、ヘッドで読み込んだ情報と現在の状態をもとに、動作と次の状態を決めます。

有限オートマトン

チューリング機械は、所要時間と記憶容量になんらの制限を置かず、電子計算機の忠実なモデルとはいえませんでした。そこで、時間と空間とに制限を置き、より忠実なモデルとして考えられたのが有限オートマトンです。

有限オートマトンは以下で構成されます。

初期状態が1つ
受理状態が有限個
それ以外の状態が有限個
入力文字の集合
現在の状態と入力、次の状態の組み合わせ

全ての入力が終わったときに受理状態にいればその入力は"受け入れ可能"と判断されます。

例を示します。入力文字={し, ぶ, ん}です。

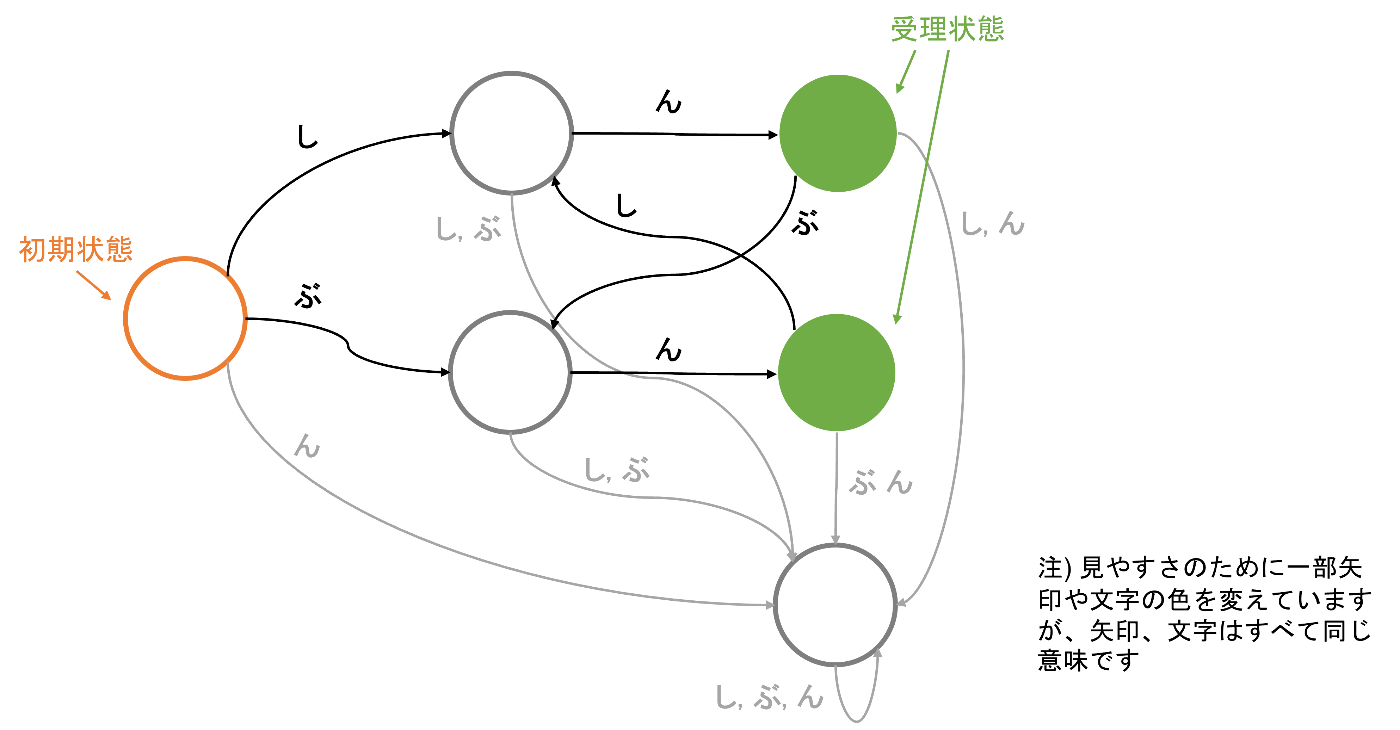
automaton

この有限ノートマトンが受理するのは"しん"や"しんぶん"、"ぶんしんぶん"、"ぶんしんぶんしん"などです。"しんぶんし"や"ぶんぶん"などは受理しません。

ニューラルネットワークの研究

話は変わって、1940年代、神経生理学者たちは、人の神経系がどのように機能しているかを研究していました。そこで様々なモデルが考え出されていました。
1943年、マカロックとピッツの2人がニューラルネットワークの基礎となる論文を発表しました(『A LOGICAL CALCULUS OF THE IDEAS IMMANENT IN NERVOUS ACTIVITY』)。この論文でで紹介されたニューロンのモデルは、(過去の状態によらず)現在の状態と入力のみによって次の状態が決まるモデルでした。

neuralnet

チョムスキー階層

一方そのころ、言語学者のチョムスキーは、言語の構造を調べていました。全ての英語の文を生成できるシンプルで明快なルールはないものかと。そこで以下のような置き換えルールを提唱しました。(例はPart2　形式言語とオートマトンを学ぶ | 日経クロステック（xTECH）から引用)

<命令文> → <動詞> <目的語>
<動詞> → help | catch
<目的語> → me | him

この場合、help me、help him、catch me、catch himの4つが命令文として受け入れられます。それ以外の文は命令文ではありません。

ここで、<動詞>、<名詞>など、ほかで置き換えが可能なものを非終端記号といい、help、meなどこれ以上置き換えられないものを終端記号といいます。

ちなみに、上記の例では矢印の左側は非終端記号が1つだけですが、複数でも構いません。

チョムスキーは上記のような置き換えルール(文法)を4つに分類しました(1956年　『THREE MODELS FOR TIE DESCRIPTION OF LANGUAG』)。

タイプ	制限	特徴	言語例
０型	なし	ステート情報をすべて保持することで、与えられた入力文字列から想定可能なあらゆる出力文字列を作成できる	自然言語
１型	`a → b`において`b`の長さが`a`以上であること	入力文字列から出力文字列までの過去のステート情報をすべて保持する	自然言語
２型	`a → b`において`a`が終端記号1つからなること	入力文字列から出力文字列までの、直近のステート情報のみを保持する	プログラミング言語
３型	`a → b`において`b`が終端記号、または終端記号のあとに非終端記号をつけること	入力文字列から出力文字列までの過去の情報を保持しない	体系化したコードなど

(自然言語とは、日本語や英語など日常の会話に使用されている言語のこと。それに対して、プログラム言語のように、厳格な文法によって生成された言語を形式言語といいます。)

こちらのページで3型の例が取り上げられています。

https://tnomura9.exblog.jp/22917549/

クリーネによる正規表現の導入

1956年、数学者のクリーネは『Representation of Events in Nerve Nets』の中でマカロックとピッツの神経回路網と有限オートマトンの関係を述べています。この論文中で用いられている、有限オートマトンで表現可能な「正規イベント (regular events)」を表現するための式 (expression) が現在「正規表現 (regular expression)」と呼ばれているものの基礎です。

正規表現の定義

記号（アルファベット） $A=\{a_{1},\dots ,a_{n}\}$ 上の正規表現は次のようなものから成る。

$\varnothing$ は正規表現である。これは記号列を何も含まない空集合 $\varnothing$ を表す。
$a_{i}$ （ $A$ の任意の要素）は正規表現である。これは $a_{i}$ という記号列のみからなる集合 $\{a_{i}\}$ を表す。
$X$ と $Y$ が正規表現ならば、
- $X\mid Y$ も正規表現である。これは $X$ に含まれる記号列の集合と $Y$ に含まれる記号列の集合の和集合を表す。
- $XY$ も正規表現である。これは $X$ に含まれる記号列に $Y$ に含まれる記号列をつなげてできる記号列の集合 $\{ab\mid a\in X,b\in Y\}$ を表す。
- $X*$ も正規表現である。これは $X$ に含まれる記号列を $0$ 個以上つなげて出来る文字列の集合 $\bigcup _{n}\{X^{n}\mid n\geq 0\}$ を表す（クリーネ閉包）。

チョムスキー再び

チョムスキーは1959年の『On certain formal properties of grammars』の中で"正規文法"を定義しています。また論文中にクリーネへの言及があります。"正規文法"の"正規"はクリーネの影響でしょうか。このあたりでそれぞれの分野の知見が1つにまとまっていったものと思われます。

クリーネとチョムスキーの定義をまとめるとこのようになります。

タイプ	文法	オートマトン	言語例
０型	-	チューリングマシン	自然言語
１型	文脈依存	線形拘束オートマトン	自然言語
２型	文脈自由	プッシュダウン・オートマトン	プログラミング言語
３型	正規	有限オートマトン	体系化したコードなど

ここまでのまとめ

正規表現の"正規"(強い制約)とは何か

定義 : 文字列集合のうち、文字の和( $X\mid Y$ )・連接( $XY$ )・クリーネ閉包( $X*$ )およびそれらの組み合わせによってのみにより表されるもの。
性質 : 有限オートマトンによって受理可能、など

正規表現は誰がいつ名付けたのか

クリーネさんが1956年に発表した論文がもとになっている。

なぜ正規であると受け入れられたのか

過去の情報を保持せず、現在の状態と入力から次の状態が決まるシステム(有限オートマトン)は取り扱いが楽であるという認識があった。また、強い制約をかけ取り扱いを楽にしたもの"正規"と呼ぶ習慣が数学界にはある。そのため有限オートマトンを1つの文字列で表現したものを、"正規表現"と呼ぶことが受け入れられたのではないか。

コンピューターへの採用

正規表現は、1970年ごろケン・トンプソンによってエディタQEDに導入されました。そして、後継のedにも受け継がれました。edからsed(1974年)、grep(1970年代前半)などが派生しました。edの後継としてex(1976年)、vi(1976年)が誕生し、正規表現の利用が受け継がれています。正規表現は今日では多くのUnixコマンドやプログラミング言語で用いられています。

正規表現は、利用の増加とともに機能が拡張され、現在では本来の正規表現では表現しきれないものも表現できています(後方参照など)。